基于SR-UKF的潜艇水动力系数辨识方法

吕帮俊，黄斌，彭利坤

海军工程大学 动力工程学院，湖北 武汉 430033

0 引 言

潜艇（或水下航行器）的高精度数学模型对其设计和性能预报起着至关重要的作用。目前，进行潜艇运动性能计算、运动规律预报或是自动操艇控制器设计，大都依赖于Gertler等[1]或是Feldman等[2]基于潜艇水动力泰勒展开推导得到的六自由度空间运动模型，以及由此简化得到的潜艇平面（水平面或垂直面）运动模型。而要精确获取上述模型方程中的各项水动力系数是建模的关键因素，但也是方程中最难以确定的，故系数精确与否将显著影响潜艇的性能计算和运动预报精度。

目前，确定上述模型的水动力系数有3种常用方法[3]。第1种是约束船模试验方法，通过定制潜艇的几何缩比模型，并开展拖曳水池、悬臂水池或者平面运动机构等水动力试验来获取。这是工程中最常用及经过实践检验后最实用和准确的一种方法，其不足之处是周期长、经费投入巨大，且试验中存在尺度效应，应用时需处理实船与船模的相关性，导致该试验方法的应用受到限制。第2种是理论计算方法，例如小展弦比理论、细长体理论等。由于流场的复杂性、流体黏性以及受到各种界面的影响，计算时必须进行一定的假设。这样做虽然方便了计算，却使得计算结果不尽如人意，导致理论结果难以满足工程要求。第3种是计算流体力学（CFD）方法，即建立三维操纵性数值水池，通过模拟开展水动力试验来获取潜艇的水动力系数。该方法相对于船模水动力试验方法较容易实现，但计算结果的精度受仿真边界条件、物性参数定义、网格划分等因素的影响较大，计算结果仍需通过水动力试验来验证。

近年来，系统辨识（system identification，SI）技术的发展为水动力系数的确定提供了新的方法[4-5]。按照一定的机动方式，在采集实船或船模航行试验的实测数据后，通过滑模观测器（sliding mode observer，SMO）[6]、卡尔曼滤波（Kalman filter，KF）[7]、序列二次规划（sequential quadratic programming，SQP）[8]、贝叶斯规则[9]等算法，可将建模所需的水动力系数准确提取出来。其中，KF是一种非常有效的系统状态预测及参数辨识算法，已在众多领域的模型参数识别领域得到有效应用[10-13]，成为近来研究的重点。为解决传统KF算法无法应用于非线性系统滤波的问题，提出了扩展卡尔曼滤波（extended Kalman filter，EKF）方法，并成为水下航行器模型参数识别方面应用最广泛的算法之一[5-6,13]。EKF算法的本质是将非线性方程局部线性化，以使得传统的KF算法能够继续适用，但该算法存在精度不高、稳定性差等缺陷。而基于无迹变换提出的无迹卡尔曼滤波（unscented Kalman filter，UKF）算法是通过设计Sigma点来近似表示n维目标采样点，并直接经由非线性函数的传播来获得更新后的滤波值，有效地克服了EKF算法的缺陷，计算精度较高。Van Der Merwe等[14]对UKF算法进行优化，解决了由误差和噪声等因素引起的误差协方差矩阵非正定性甚至是计算发散的问题，提出的平方根无迹卡尔曼滤波（SR-UKF）算法已逐步应用于水下航行器数学模型未知参数识别[15]。SR-UKF算法利用协方差平方根代替协方差参加递推运算，保证了滤波算法的数值稳定性，能提高跟踪的精度和可靠性。尝试应用SR-UKF算法辨识潜艇水动力系数，探索新的系统识别技术在未知参数识别方面的潜力，对于精确建立潜艇操纵运动数学模型并准确预报潜艇的运动和性能具有重要意义。

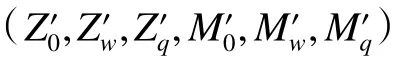
1 潜艇垂直面操纵运动数学模型

采用国际拖曳水池会议（ITTC）推荐的和美国造船与轮机工程学会（SNAME）术语公报的体系[16]，对Gertler等[1]发表的用于描述潜艇空间运动的方程进行如下假设：

1） 潜艇在水平方向受到的力和力矩平衡，忽略水平方向运动对操纵的影响；

2） 潜艇在垂直面内作弱机动，即垂向速度w、俯仰角速度q、艏舵角δb和艉舵角δs等运动参数为小量；

3） 认为潜艇航速u=u0保持不变，可忽略X方程。

得到潜艇垂直面操纵运动数学模型为：

图 1 描述潜艇垂直面运动的坐标系和主要参数Fig.1 The coordinate system and main parameters for describing submarine motion in the vertical plane

将式（1）～式（4）改写成矩阵形式以便积分求解。

式中：x=[ζ，θ，w，q]T，为状态变量；u=[δb，δs]T，为控制输入；

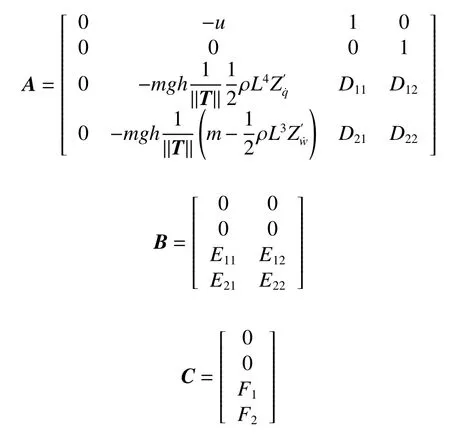
其中，

2 SR-UKF算法及辨识模型

SR-UKF算法用于参数估计时，一般可分为3个基本步骤[14]循环迭代，直至收敛到固定值。

2.1 初始化

当迭代次数k=0时，

2.2 时间更新和Sigma点计算

采 用k-1步的 均 值wˆk-1和 协方 差 矩阵Swk-1构造Sigma点，预测下一步的系统状态均值和方差。

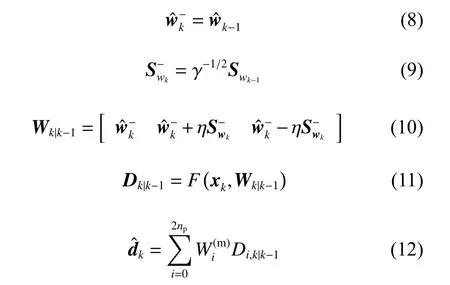
Sigma点权值：

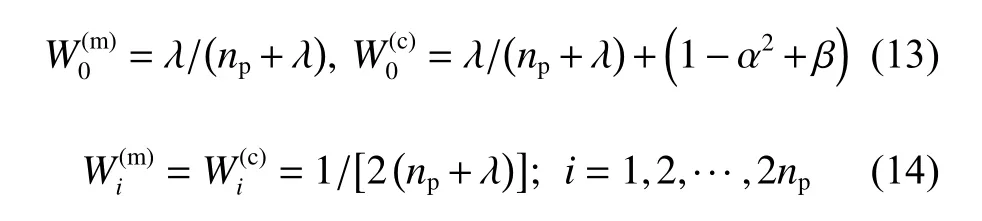
式（11）需要采用离散方程的形式估算2np+1个Sigma点的非线性函数值，可将式（5）写成

式（15）给出的微分方程通常可采用四阶龙格-库塔积分算法进行积分，设积分步长为 Δt：

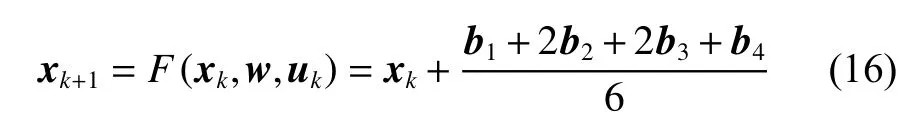
式中：b1=F(xk,w,uk)Δt；b2=F(xk+0.5b1,w,uk)Δt；b3=F(xk+0.5b2,w,uk)Δt；b4=F(xk+b3,w,uk)Δt。

2.3 测量更新

式中： qr(·)为进行矩阵的QR分解； cholupdate(·)为进行矩阵乔列斯基分解因子更新；Re为测量误差协方差矩阵；dk为观测向量，对于潜艇的垂直面运动，可取dk=[θk,wk,qk]T，也即采用潜艇的纵倾角、垂向速度以及纵倾角速度作为测量值。

3 水动力系数辨识

采用SR-UKF算法辨识参数时，为得到观测向量dk，实艇一般采用多普勒仪（DVL）、陀螺仪或是姿态航向参考系统（AHRS）来采集潜艇的运动参数，以用于水动力系数估计[17]。因仅研究算法的可行性，故只采用数值仿真方法得到所需的运动参数，并加入一定的测量噪声来模拟实际传感器的测量值。此外，为使所有水动力系数都能得到有效辨识，必须设计一种潜艇机动模式，用以激发所有的水动力分量。本文设计自动操舵控制算法来使潜艇在垂直面采用近似正弦的操纵运动规律，初始航速取为6 kn，参数随时间变化的情况如图2所示。为避免机动过程的规律性太强而导致辨识结果不收敛，2 500 s之后通过艏舵控制放缓深度变化频率，同时增大深度变化范围。

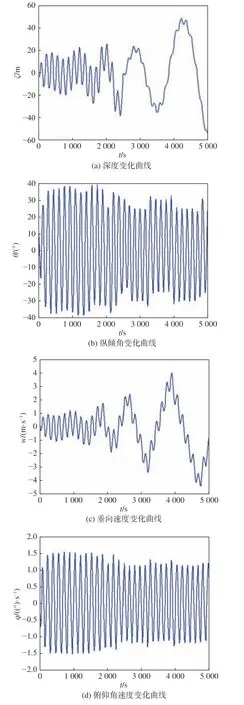
图 2 潜艇在垂直面的机动形式Fig.2 Submarine manoeuvring in the vertical plane

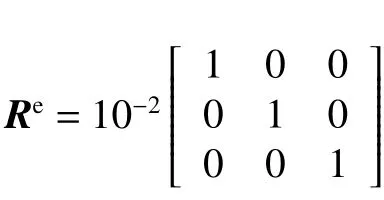
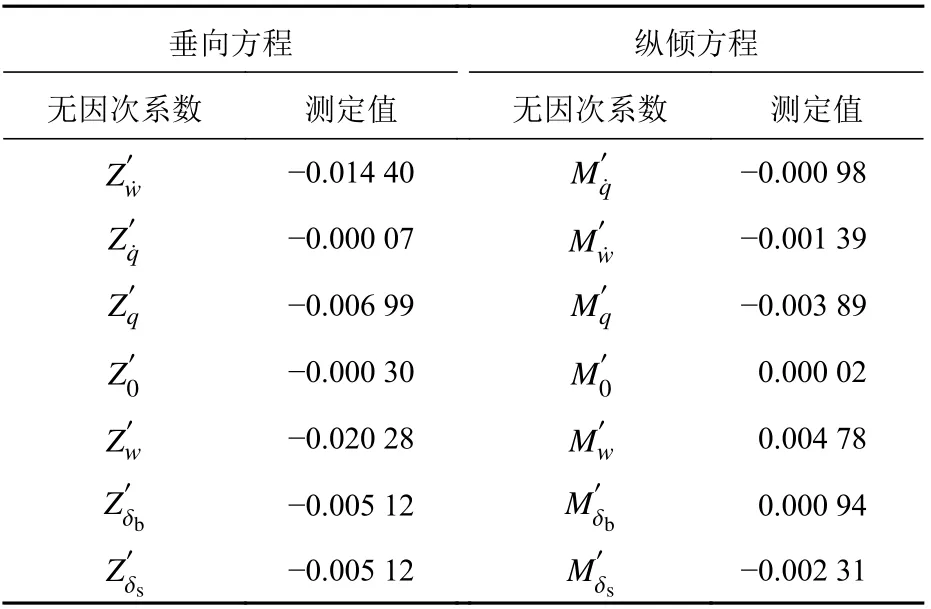
表 1 无因次水动力系数测定值Table 1 Dimensionless hydrodynamic coefficients measured values

当初值w0均为0时，6个水动力系数随时间的收敛情况如图3所示。从中可以看出，算法经过约3 000 s后，所有的水动力系数均逐渐收敛为一个常数。将各系数辨识结果与表1中的水动力试验测定标准值进行比较，误差百分比（|辨识值-真实值|/真实值×100%）如表2所示。表中所列水动力系数除了M0′的误差达到了1.5%以外，其余水动力系数的辨识误差均在1%以内。此外，当水动力系数初值w0取[0，1]区间内的随机数时，仿真辨识也可得到如图3中所示的类似收敛曲线，此处不再重复列举。表中误差最大的仍然是M0′，约达37%，其他参数辨识的最大误差均在3%以内。其主要原因是，M0′的水动力试验测定值本身非常小，仅 2×10-5，所以即使是很小的绝对误差，也会引起较大的误差百分比。

图 3 SR-UKF算法的辨识结果Fig.3 Identification results by SR-UKF

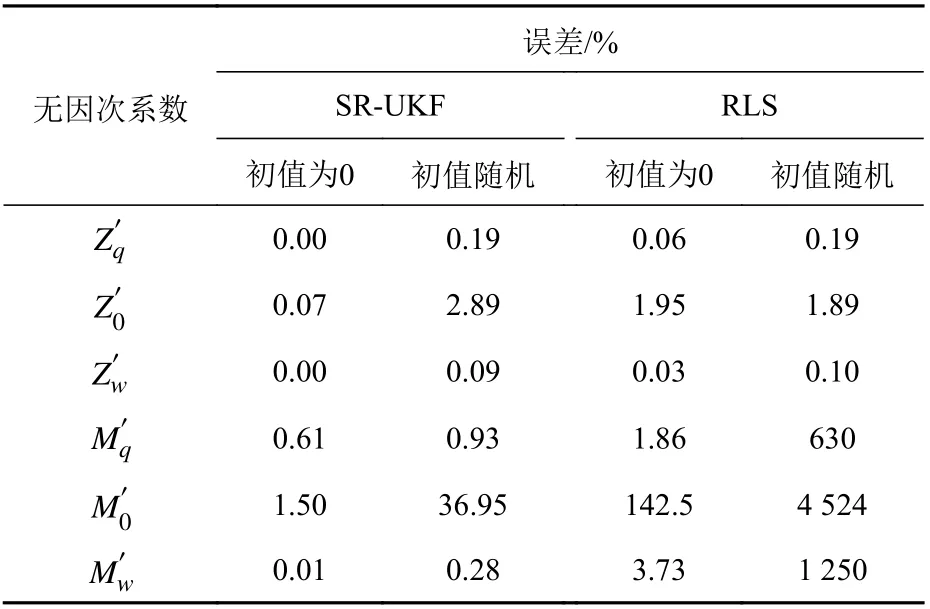
表 2 无因次水动力系数辨识误差Table 2 Dimensionless hydrodynamic coefficients identification errors

图 4 RLS算法的辨识结果Fig.4 Identification results by RLS

4 结 语

本文将SR-UKF算法应用到了潜艇垂直面黏性类水动力系数识别中，该算法直接采用非线性系统的状态方差矩阵和噪声方差矩阵的平方根进行递推与估算，有效避免了采用传统UKF算法进行参数辨识时因参数设置不合理而导致的噪声方差矩阵非正定性等问题。该算法运行稳定，当待辨识参数选取合适的初始值时，采用潜艇的垂向速度、纵倾角和纵倾角速度仿真数据作为测量输入进行参数辨识最大误差仅1.5%，完全能够满足工程实际要求，并可以作为一种有效的水动力系数识别方法用于实船的水动力系数识别。