喷水推进船骑浪运动建模及时域仿真
封培元,蔡佑林,范佘明
1 喷水推进技术重点实验室,上海 201100
2 上海市船舶工程重点实验室,上海 200011
3 中国船舶及海洋工程设计研究院,上海 200011
0 引 言
完整稳性是船舶安全性设计最重要的性能指标之一,国际海事组织(IMO)为此制定了强制性的法规规范以保证船舶具备足够的完整稳性。随着新概念船型的不断涌现,船舶大型化发展趋势愈发明显,现行的船舶完整稳性衡准对新船的适用性问题日渐受到业内关注。因此,IMO从2009年开始制定新的船舶第二代完整稳性衡准(以下称二代稳性衡准),经过10年反复论证,于2019年在英国伦敦召开的船舶设计与建造分委会第6次(SDC 6)会议上通过了全部规范内容[1]。因此,二代稳性衡准作为现行规范的补充和替代方案,未来将改变以往依靠经验公式来制定衡准的方法,而引入稳性直接评估的概念,为新概念、超尺度比船舶提供个性化的稳性评估方法。在二代稳性衡准纳入强制性规范后,若船型不能满足要求则需改进,待符合要求后才可进入国际船舶市场,所以这是我国船舶设计研究单位面临的重要而急迫的任务,也是国内造船工业发展必须面对的巨大挑战[2]。
骑浪/横甩是二代稳性衡准规范中的5种稳性失效模式之一。在随浪中,高速航行的船舶突然失去航向保持能力并发生急速转向的现象被称为横甩。发生横甩时,船舶尽管使用了最大舵角,但仍不能维持预定航向,且伴有猛烈的艏摇,同时产生大角度横倾,直接危及舰船在波浪中的航行性能和安全;而骑浪则是导致横甩的先决条件,航行实践和船模试验均表明骑浪是一种十分危险的状态。因此,IMO在二代稳性衡准规范中要求直接针对骑浪进行校核。
由力学分析结果可见,船舶骑浪状态是纵向波浪力、推力和阻力在船速等于波速时达到的动力平衡的平衡时态。迄今,预报船舶骑浪运动采用的主要方法包括解析方法[3-5]、模型试验方法[6]和数值仿真方法[7]。现行的骑浪/横甩第2层薄弱性衡准校核是基于非线性动力学中的分叉理论,采用Melnikov方法求解船舶骑浪时的临界螺旋桨转速,并以此为依据来判断船舶是否存在骑浪的危险。
喷水推进是一种特殊的船舶推进方式,与传统的螺旋桨推进船相比,喷水推进船的机动性和操纵性优良,可在浅吃水下工作,具有水声特征信号小、高航速时推进效率高、抗汽蚀能力强等优点,在国际船舶工业领域(尤其是高性能船舶领域)得到了广泛应用。但是,喷水推进船同样也存在发生骑浪的风险,而现行规范仅适用于螺旋桨推进船舶,如果要对喷水推进船进行二代完整稳性衡准的校核,在船型适用性方面尚存在局限性。
鉴此,本文将基于喷水推进装置的力学模型和船舶在随浪中的一维纵荡运动方程,构建喷水推进船的骑浪运动数学模型,利用四阶Runge-Kutta法求解该运动模型,以实现喷水推进船的时域运动仿真;通过开展时域数值计算,得出船舶发生骑浪现象的工况特点,为喷水推进船骑浪/横甩稳性评估提供理论模型和数值分析手段。
1 喷水推进船的骑浪运动模型
1.1 喷水推进力学模型
喷水推进系统的推力特性主要由以下2个公式描述[8]。其中,式(1)为基于动量守恒定理得到的推力方程,描述了水流经喷泵加速后的动量变化与所产生推力之间的平衡关系;式(2)为基于能量守恒定理得到的扬程方程,描述了流经喷泵的水流动能、势能和流动损失之和应等于喷泵提供给水流的能量这一平衡关系。

式中:T为喷水推进系统能够产生的推力;Q为流量;ρ为水介质密度;Vj,V0分别为喷射速度和平均进流速度;α为船体边界层对进流动量的影响系数;H为喷泵的扬程;g为重力加速度;hc为喷口中心距静水面高度;kj,ki分别为喷口处的流动损失系数和进水流道的流动损失系数;β为冲压利用系数,其反映了船体边界层对进流动能的影响程度,一般有[9]:

在预报喷水推进系统的推进性能时,ρ,g和hc为已知量;kj,ki表征的是动量和能量损失的系数,若缺少准确数据,一般可参照经验值选取[8],例如:kj=0.02~0.03;ki=0.2~0.3;α=0.85~0.9。
1.2 喷水推进船骑浪运动模型
规则波中的船舶骑浪运动数学模型涉及了如图1所示的3个坐标系:与大地固结的惯性坐标系OE-XEZE,船舶在惯性坐标系中以航速VS沿波浪传播方向前进;波浪坐标系O-ξζ,坐标原点O的纵向位置对应波谷,并以波速cW在惯性坐标系中移动;与船体固结的运动坐标系G-xz,坐标原点G的纵向位置对应船舶重心,G和O之间的纵向距离表征了船舶相对波浪所处的位置。图中, ξG/λ为船舶相对波浪的位置,其中λ为波长。
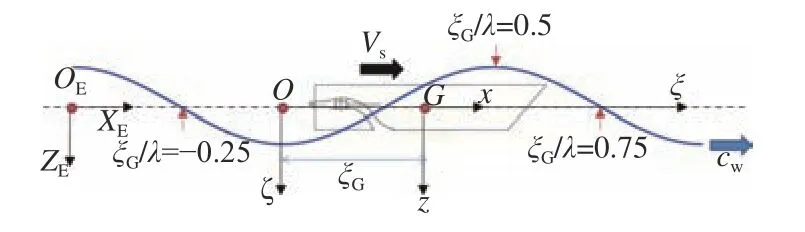
图 1 骑浪运动模型坐标系Fig.1 Coordinate system of the surf-riding model
骑浪运动数学方程以船舶在随浪中的单自由度纵荡运动方程为基础,建立船舶受到的阻力、波浪力和惯性力与喷水推进系统产生的推力之间的平衡关系,如式(4)所示。
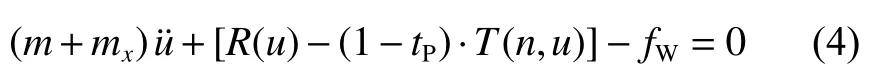
式中:m为船舶质量;mx为纵荡附加质量;u为惯性坐标系下船舶的实时纵荡速度;u¨为纵荡加速度;R为船舶受到的阻力;T为喷泵转速n和u的函数;tP为推力减额系数;fW为船舶受到的波浪纵荡力。
由惯性坐标系与波浪坐标系之间的变换关系,可推导得出波浪坐标系下的骑浪运动数学方程:
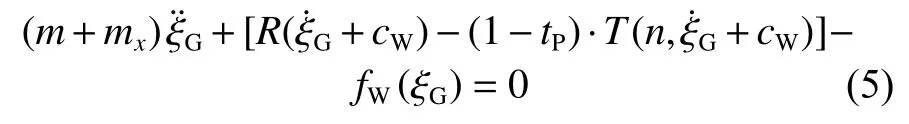
式中, ξG为波浪坐标系下船舶相对坐标原点的纵向位置,上方的点表示对时间求导。
由于针对喷水推进船的骑浪运动建模其难点在于航速在波浪力作用下会随时发生变化,进而影响喷泵的进流速度,改变喷水推进系统产生的推力,所以正确预报喷水推进系统在变航速下实时产生的推力是建模关键。对骑浪运动建模而言,喷水推进船与螺旋桨推进船这两者间的差异也主要体现在推进模型方面,其他的阻力和波浪力等成分可根据IMO二代稳性规范中的相关要求建模。
船舶阻力采用多项式拟合的方式模拟:
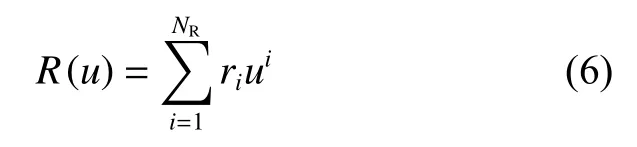
式中:NR为拟合阶数,IMO建议用三阶或五阶多项式进行拟合;ri为拟合后的系数。
喷水推进系统的推力模型是本研究的重点。为预报喷水推进系统在变航速下的实时推力,需建立喷泵的扬程平衡关系。式(2)所示为喷水推进系统产生一定推力时所需的扬程,而喷泵是否有能力达到该扬程则由喷泵自身的水力特性决定。依据文献[10],喷泵所能提供的扬程可在喷泵模型试验数据的基础上由下式近似表达:
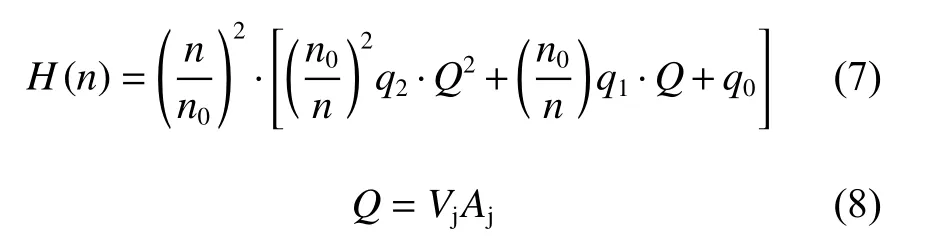
式中:n0为喷泵额定转速;q0,q1,q2为对应n0的扬程流量H-Q曲线测试结果的拟合系数;Aj为喷口面积。
本文模型中,认为喷泵的平均进流速度V0等于实时纵荡速度u,在喷泵转速n保持不变的情况下,通过联立式(2)和式(7)即可获得当前时刻下喷泵的实际流量,再利用式(1),便可计算得到此时喷水推进系统产生的推力。
波浪纵荡力fW的建模同样参照IMO规范要求,具体如下:
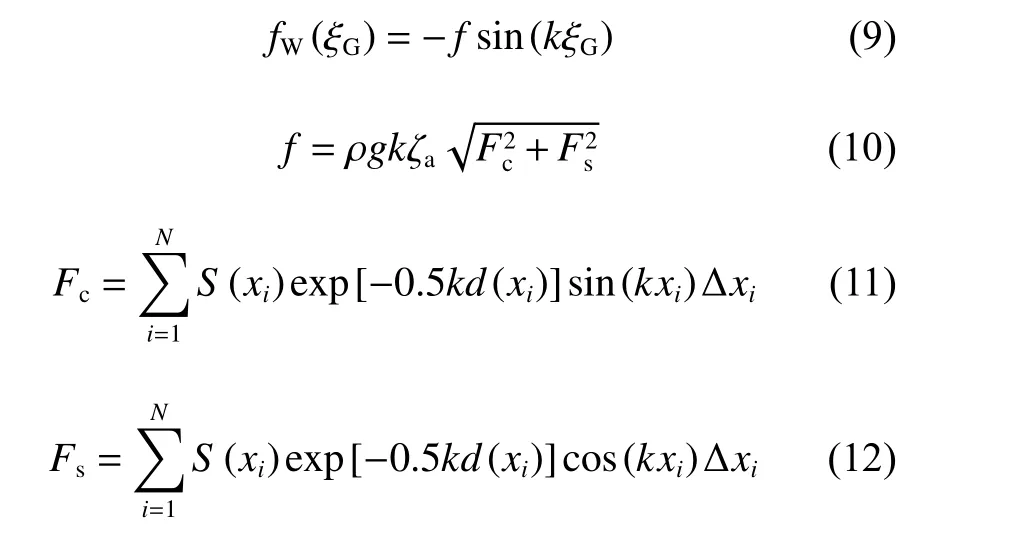
式中:k为波数;ζa为规则波波幅;xi为惯性坐标系下各站船剖面的纵坐标;d(xi)为静水中各剖面吃水;S(xi)为静水中各剖面浸没面积;N为站数;f为幅值;Fc和Fs分别为力的正弦分量和余弦分量。
2 喷水推进船骑浪运动时域仿真
采用四阶Runge-Kutta法求解式(5)对应的常微分方程,可得到船舶相对于波浪速度的时历。若最终该速度趋近于0(航速与波速相等),则说明船舶发生了骑浪; 否则,船舶将在波浪作用下出现周期性运动。下文将以某高速穿浪式内倾船型为例,通过时域数值计算研究该类型船舶发生骑浪现象的工况特点。
2.1 目标船参数
目标船为一艘采用喷水推进方式的高速穿浪内倾船,如图2所示,其主要参数如表1所示。该船安装有4台混流式喷水推进装置,设计航速对应的弗劳德数Fr=0.4。目标船的质量m=2 834 t,参照IMO规范,取纵荡附加质量mx=0.1 m,根据模型试验结果,取推力减额系数tP=0.02。目标船的阻力数据基于模型试验获得,并通过三次多项式进行拟合。喷泵的水力性能参数由台架试验获得,换算到实际的泵后的结果如图3所示。图中,圆点对应喷泵在额定转速下的试验结果,实线为试验点的二次多项式拟合曲线。该喷泵对应的各系数取值如下:kj=0.020 3;ki=0.24;α=0.88。

图 2 目标穿浪内倾船型线Fig.2 Wave-piercing tumblehome hull lines of the sample ship
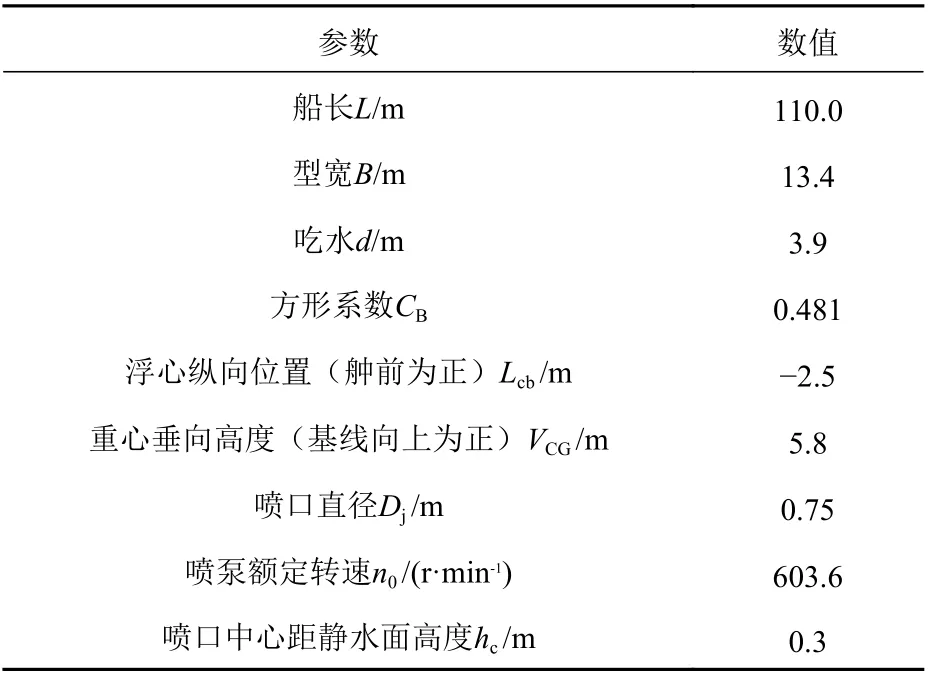
表 1 目标船主要参数Table 1 Main particulars of target ship
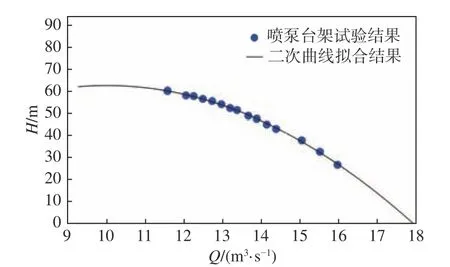
图 3 喷泵水力性能试验结果Fig.3 Experimental results of pump's hydraulic performance
2.2 时域仿真计算结果
对设计航速(Fr=0.4)下的典型规则波工况进行数值仿真计算。在波长船长比λ/L=1.5、波陡H/λ=0.05的随浪规则波中,目标船相对于波浪的位置 ξG/λ及速度仿真结果如图4所示。由图4可见,船舶相对于波浪的位置在几个周期的短暂振荡后达到一个稳定值,相对于波浪的速度也趋向于0,这表明在该工况下目标船发生了骑浪。
图5所示为在上述典型规则波工况下目标船的受力时历曲线。经对其进一步分析可知:在初始状态下船舶航速低于波速,在波浪力的作用下船舶被加速,此时静水阻力更大;同时,喷泵进口的流速加快,喷泵推力却有所降低;在波浪力、阻力和推力的共同作用下船舶在约60 s后达到平衡状态。
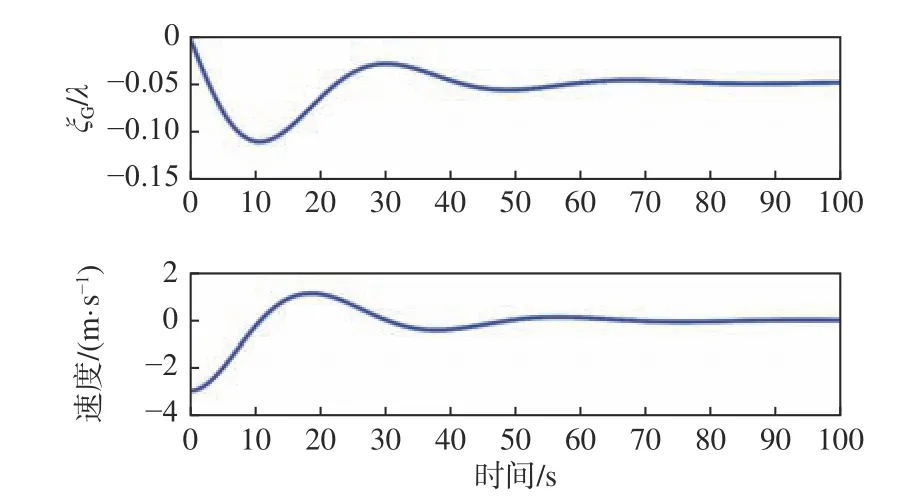
图 4 目标船相对于波浪的位置及速度仿真结果(Fr=0.4, λ/L=1.5,H/λ=0.05)Fig.4 Simulation results of the sample ship's position and speed relative to wave (Fr=0.4, λ/L=1.5, H/λ=0.05)

图 5 目标船的受力仿真结果(Fr=0.4, λ/L=1.5, H/λ=0.05)Fig.5 Simulation results of forces acting on the the sample ship(Fr=0.4, λ/L=1.5, H/λ=0.05)
为进行对比,图6和图7给出了λ/L增大至2.5后的仿真结果。由于此时的波速显著高于船速,船舶无法实现骑浪时的平衡状态,所以相对于波浪的位置船舶在不断退后,而相对于波浪的速度和受力等则呈现出周期性的振荡现象。
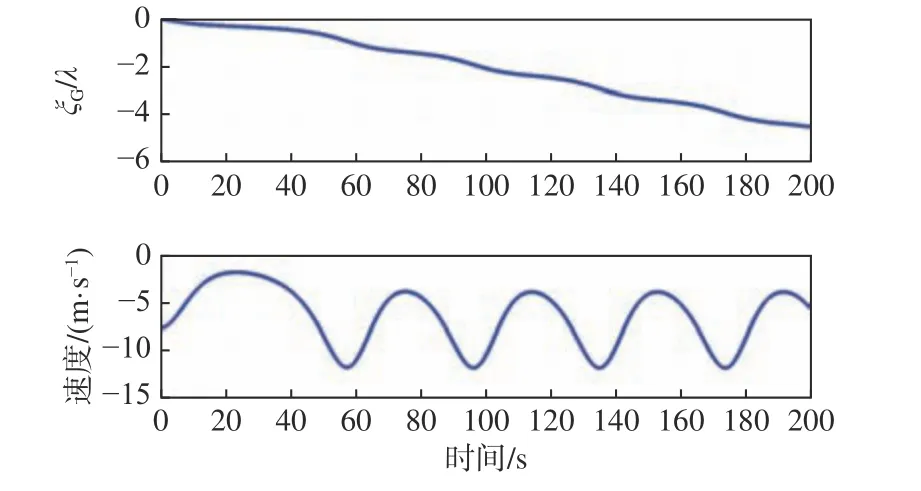
图 6 目标船相对于波浪的位置及速度仿真结果(Fr=0.4,λ/L=2.5, H/λ=0.05)Fig.6 Simulation results of the sample ship's position and speed relative to wave (Fr=0.4, λ/L=2.5, H/λ= 0.05)
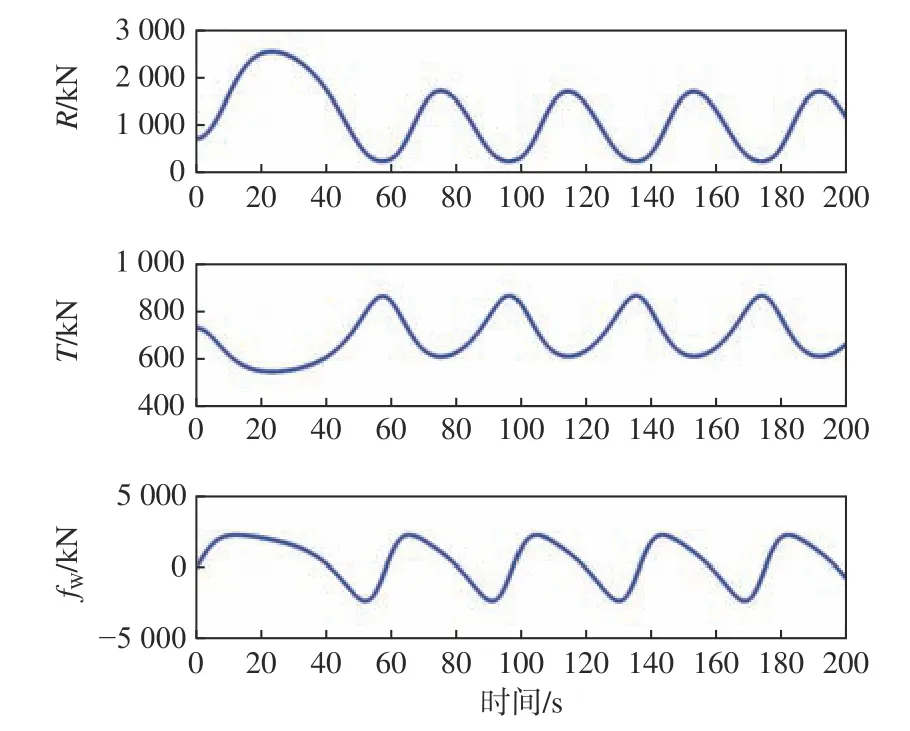
图 7 目标船的受力仿真结果(Fr=0.4, λ/L=2.5, H/λ=0.05)Fig.7 Simulation results of forces acting on the sample ship(Fr=0.4, λ/L=2.5, H/λ= 0.05)
利用本文提出的骑浪运动模型和时域仿真方法,对IMO骑浪/横甩第2层薄弱性衡准校核中要求的λ/L和H/λ范围进行计算研究,分别对比 航 速 对 应 的Fr=0.4(n=513.4 r/min)和Fr=0.3(n=349.3 r/min)时骑浪发生的工况,如图8所示。图中,深色对应未发生骑浪的区域,浅色对应发生骑浪的区域。根据图8所示横轴对应的波陡范围(H/λ=0.03~0.15)和纵轴对应的波长船长比范围(λ/L=1.0~3.0),总计对320个工况进行了仿真计算。所选取的工况范围符合IMO二代稳性骑浪/横甩第2层薄弱性衡准的要求,在该工况范围内,船舶骑浪后再横甩的可能性较大。
计算结果表明:Fr=0.4时,发生骑浪的工况比例高达80.9%;Fr=0.3时,发生骑浪的工况比例减小为59.4%。从发生骑浪区域的分布来看:在λ/L接近1时,船舶在较小的波陡H/λ就将发生骑浪;随着λ/L的增大,发生骑浪所需的最低波陡H/λ也随之增大。因此,目标船在波长与船长相近的情况下更易发生骑浪,而降低船速可以有效减少发生骑浪工况的比例。仿真计算结果表明,船舶发生骑浪后相对于波浪的最终平衡位置,绝大部分情况位于波浪的下坡面,此时更有可能进一步发生横甩。
3 结 语
本文针对当前IMO船舶二代稳性衡准仅适用于螺旋桨推进船的局限性,基于喷水推进装置的力学模型和船舶在随浪中的一维纵荡运动方程,建立了喷水推进船的骑浪运动数学模型,为喷水推进船的骑浪/横甩稳性评估提供了理论模型和数值分析手段,可服务于此类船舶的稳性安全评估。并以一艘高速穿浪内倾船为例,通过系统性地开展时域数值计算,得出了该类型船舶发生骑浪现象的工况特点。结果表明,目标船在波长与船长相近的情况下更容易发生骑浪,而降低船速可以有效减少发生骑浪的风险。
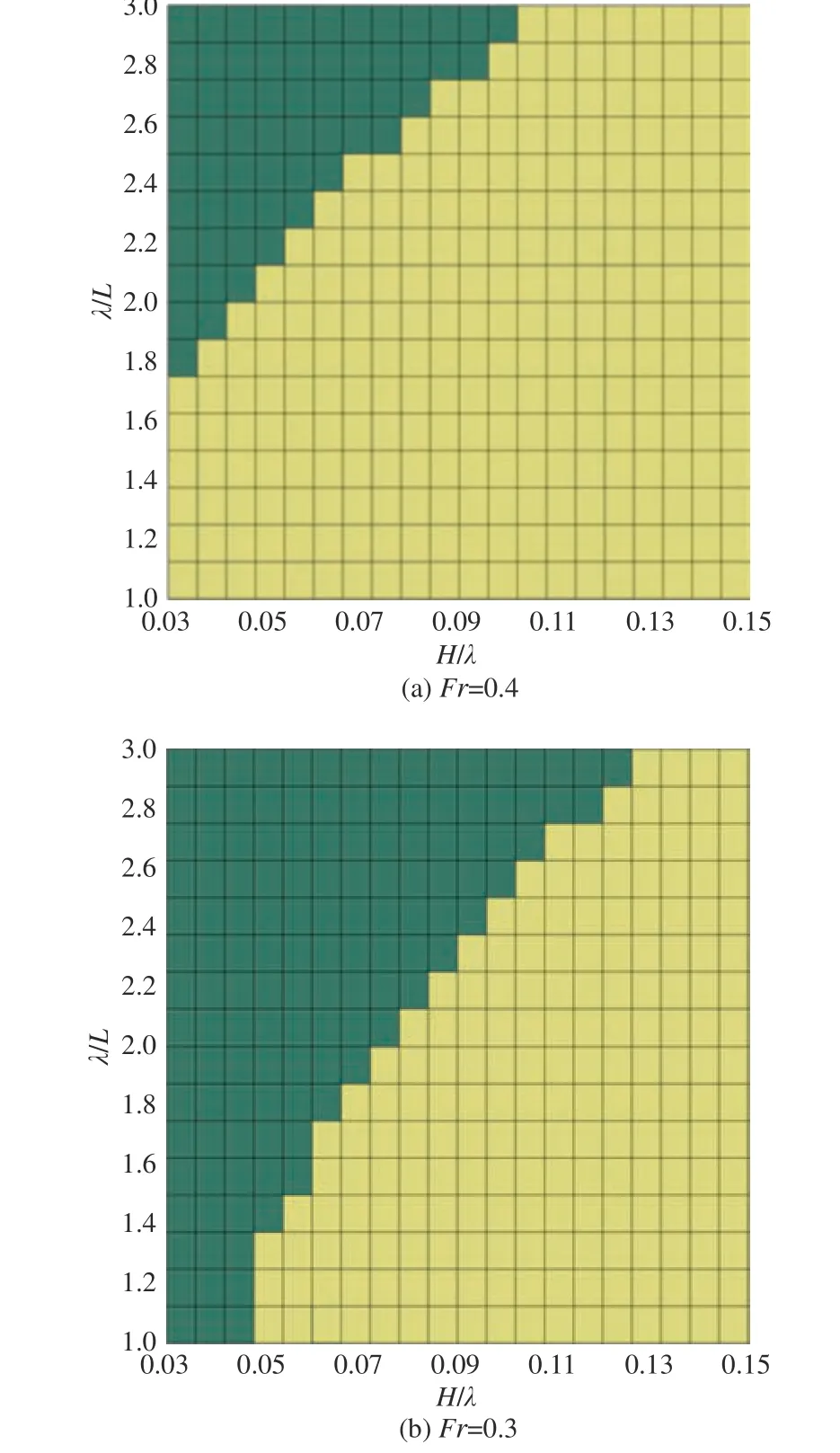
图 8 骑浪发生工况的仿真结果Fig.8 Simulation results of the surf-riding occurrence conditions
基于本研究,未来可进一步建立多自由度的喷水推进船运动模型。而为模拟横甩运动,需至少建立包括纵荡-横荡-艏摇-横摇运动模态的4个自由度操纵运动模型,同时,还需对喷水推进船在波浪中的受力进行建模。

