多方法融合视角下的中国最好大学评估检验

胡泽文 曹玲 尹献

关键词：高校评估;大学排名;评价指标;TOPSIS模型;面板数据模型;层次分析模型;灰色关联模型

高校排名主要通过制定经过科学论证的评估标准和评估方法，对高校的科研活动和科研成果给予科学计算和评估之后得出综合评分或排名。评估结果可以作为一种价值尺度，促进高校发展，使高校能够清晰直观了解到在教学、科研、国际化以及学术成就等诸多方面指标上的优点和不足之处，为学生择校、政府资助、项目和资金支持、高校自我认识和改进提供一个基准参考。然而目前国内外高校评估实践在评价指标选择和指标权重确定方面仍存在较多的主观成分.定量化的客观评估实践相对较少。戴跃依认为评价目的和评价指标体系的不同会影响到评价和排名结果。因此“如何克服指标选择和权重确定过程中的主观性，使其对价值主体的影响最小化.使评价更具客观性”是当前高校评估领域亟需解决的重点难点问题。施艳萍等和郭丛斌等从指标多样性、权重分配、文献数据和声誉数据来源等维度对世界主流的大学排名指标体系特征进行分析，发现THE世界大学排名指标体系最为全面和均衡;QS指标体系相对简单，声誉等主观因素的比重较高;US News世界大学排名指标体系重视科研，文献类客观指标比重较大。不同高校评估机构在评估指标、权重和方法方面的创新性和差异性，会导致不同评估机构给出的高校排名结果之间有所差异，使得这些榜单排名给参考人员带来困惑。

国际性高校评估与排名实践相对较早.1986年和1987年，《泰晤士高等教育》和美国新闻与世界报道分别推出了英国高等学校排名和美国最佳大学排名，排名不仅对高校进行整体排名，而且进行了分学科排名和分学位等级阶段。2004年开始，《泰晤士高等教育》与教育网络机构QS（Quac.quarelli Symonds）公司共同推出世界大学排名。然而2009年开始，《泰晤士高等教育》和QS公司终止合作，开始单独推出自己的世界大学排名。21世纪初，中国的一些社会团体、政府组织或高等教育机构受国际大学评价的影响，开始尝试对中国的大学进行评估排名。例如：2003年开始的中国校友会大学排行榜，2004年武汉大学中国科学评价研究中心推出的中国大学竞争力排行榜（简称中评榜），以及2015年上海软科教育信息咨询有限公司推出的中国最好大学排名榜（原为上海交通大学世界一流大学排名）。面对各类不同机构推出的大学排行榜，国内外学者提出一些质疑与建议。胡咏梅认为网大高校排名指标体系中涉及科研评价的指标权重过大，会使高校不重视“人才培养”这一基本职能。夏振荣等发现建校历史、私立大学和英语大国高校对大学排名具有正面影响，而办学历史、地域条件和大学性质对大学排名的影响是有限的。李鹏虎发现上海交通大学世界大学学术排名的排名指标体系中，数据覆盖面单一，论文指标来源多为英文刊物.对德国和法国等一些非英语国家的顶尖大学有失公平。

此外，胡泽文等全面系统性阐述和比较分析了国际代表性高校评估和排名实践在评估时采用的特色指标和特色评估方法.为国内高校评估实践提出一些建议：评估单元应该细化到具体学科和专业，不同评估单元应该有不同的指标和权重;应注重科研商业化活动的评估：量化评估与同行评议应该结合起来;评估应该考虑市场化因素;评估时不仅要注重存量指标，也应该注重流量指标;应考虑相对影响、高被引和低被引指标的使用。国际学者Aguillo I F等分别测度了5种国际性高校排名实践之间的相似性，发现Quacquarelli Symonds公司和西班牙国家研究委员会网络计量学实验室的欧洲大学排名结果之间存在较大差异，而中国台湾地区财团法人高等教育评比中心基金会和荷兰莱顿大学科学技术研究所提供的欧洲大学排名结果相似度较高。Barreto P D和Hans P H发现政治经济和文化环境因素、资金和领导是影响高校名次涨落的重要因素，高校排名也会导致资助的偏见，排名靠前的高校能够获得更多经费资助。此外，高敏等通过统计分析2016年中国最好大学排名TOPl00高校的区域差异性，发现国内百强高校基本呈现东部多西部少、南部多北部少的分布态势，区域经济发展水平和富裕程度对高校排名的影响较大。

1数据与研究方法

首先将中国最好大学排行榜中TOP100高校在2015-2018年历年的不同评价指标数据及排名结果组成面板数据，实现融合面板数据模型和层次分析模型的指标新权重测算，然后以2017年中国最好大学排行榜的TOP100高校作为评估对象，分别实现基于不同权重和不同定量评估方法的高校评估实践，并对排名结果进行综合对比分析。

1.1中国最好大学排名指标体系

中国最好大学排名是由上海软科教育信息咨询公司基于第三方公开数据，采用客观透明的评价指标体系和排名方法，对国内大学进行排名。自2015年開始，每年发布中国最好大学排名榜。该排名2015年并未加入社会声誉这一指标，但在2018年才开始将培养结果指标权重从15%更改为10%，加入社会声誉指标，并将权重设定为5%。其余指标保持不变。2018年中国最好大学排名榜单采用的指标及权重如表1所示（http：//cnews.chinadai.1y.com.cn/2018-02/27/content_35746829.htm）。

由表1可知，中国最好大学排行榜采用的指标均是可以通过统计数据测度的硬性指标.其中人才培养类指标的权重最高，达到45%。人才培养类指标中，生源质量指标最受重视，权重高达30%，并将社会声誉指标作为人才培养类指标的一部分。中国最好大学排名也非常重视服务社会指标和国际化指标，权重分别达到10%和5%。

此外，一级指标中，科学研究占比达到40%，其二级指标一科研规模、科研质量、顶尖成果和顶尖人才的指标权重采用平均分配的原则.各占10%。中国最好大学排名对于生源和科研两项指标最为重视，总权重达到85%。该指标体系采用的指标数据均来自第三方数据库，论文数量、论文质量、高被引论文、高被引学者数据均来自Scopus数据库。生源质量、培养结果及社会声誉等指标数据则采用省级教育部和统计年鉴等发布的数据。因此指标数据具有可获取性和客观性。

1.2面板数据构建

面板数据是时间序列和截面混合数据，指截面上不同个体在不同时点上观测的二维数据。通过面板数据模型测算高校评估指标权重是权重定量测度的新思路。面板数据主要由2015-2018年中国最好大学排行榜Top100高校的各指标得分数据和综合得分数据组成，具体构建过程如下：首先基于原始数据和指标权重测算出Top100高校每个指标的得分数据和综合得分数据，然后筛选出2015-2018年期间连续在前100名中出现的高校指标及综合得分数据组成面板数据。高校指标数据中剔除了只在2015年和2016年出现的“产学研合作（校企合作论文）”指标，以及只在2018年出现的“社会捐赠”指标、只在2017年和2018年出现的“学生国际化（留学生比例）”指标，现共有指标8个。部分高校2015-2018年期间指标及其综合得分的面板数据如表2所示（https：//www.shang.hairanking，cn/rankings/bcur/201611）。

1.3研究方法

首先将表2面板数据中反映高校综合质量的总分设置为因变量，并标记为Y，反映高校不同维度质量的指标作为自变量.各个自变量的标记分别为：生源质量得分（X1）、培养成果得分（X2）、科研规模得分（X3）、科研质量得分（X4）、顶尖成果得分（X5）、顶尖人才得分（X6）、科技服务得分（X7）和成果转化得分（X8）。同时根据中国最好大学排名指标体系，将反映高校综合质量的所有指标进行分层，形成高校综合质量评估的层次结构模型，如表3所示，涵盖评估目标：高校综合质量，标记为字母0;3个一级指标A1、A2和A3;A1的两个二级指标X1和X2，标记为字母B1和B2;A2的4个二级指标X3～X6，标记为C1～C4;A3的两个二级指标X7和X8，标记为D1和D2。

然后通过构建反映自变量（X1～X2）与因变量（Y）之间多元回归关系的面板数据模型，借助计量经济学软件包EViews工具，量化分析各评估指标对高校综合排名的重要性，得出反映各指标重要性的回归系数，同时基于各层指标系数之间差值的绝对值大小，建立判断指标之间相对重要性的标准，利用层次分析法构建各层指标相对重要性的判断矩阵.并基于判断矩阵，利用数学函数测算新的指标权重。最后融合新的指标权重，借助Excel工具，综合运用各类量化评估方法：TOPSIS法、改进型TOPSIS和灰色关联法对高校排名进行评估检验，并与原始指标权重的评估结果进行对比分析。个体固体效应模型和混合模型是面板数据模型的两种类型，个体固体效应模型的数学表达式为：

其中i=1，2，…，N;t=1，2，…T，混合模型也称不变参数模型，即所有截面的截距相同（截距c为常数），系数相同（自变量前的系数β不变）。此外，层次分析法、TOPSIS法和灰色关联法的数学原理、评估过程和评估实践参考胡泽文主编的书藉《信息资源评估理论与实践》。

2融合面板模型和层次分析法的新权重测算

2.1面板数据选择与分析

将Y作为因变量，X1～X2作为自变量，分别采用混合模型（Pooled Regression Model）和个体固定效应回归模型（Fixed Effects Regression Model）对表2所示TOP100中国高校组成的面板数据进行拟合分析，结果如表4所示。

为了检验固定效应模型是否比混合模型更合适表2面板数据的拟合，冗余性F检验被采用。F检验假设：

H0：模型中不同个体的截距相同。

H1：模型中不同个体的截距项a不同。

检验结果显示F检验的概率为0.408.概率不显著，表示接受零假设.因此应该摒弃固定效应模型，选择混合效应模型。根据表4中8个指标变量与评价总得分之间的回归系数关系，构建混合模型的数学表达式：

2.2融合层次分析法的指标相对重要性标准建立

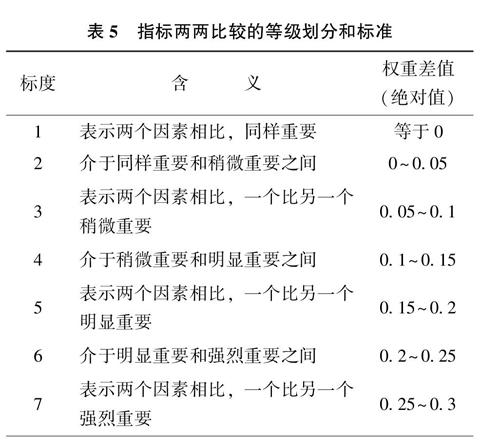
判断矩阵作为层次分析法的计算基础，矩阵元素的值是人们对各因素相对重要性认识的反映，对决策效果或评估结果会产生直接重要的影响。判断矩阵的元素一般采用1～9及其倒数的标度方法。但由于具体情况的不同，笔者结合Saaty教授提出的“1～9标度方法”.建立反映各指标相对重要性的判断标准，从而形成高校评价指标层次结构模型及其对应的判断矩阵。通过分析反映各指标重要性的回归系数及其差值大小（表4混合模型拟合结果），发现各指标回归系数差值的绝对值主要在0～0.5之间.因此对传统“1～9标度”的相对重要性标准依据指标系数差值的绝对值区间进行重新设定为：差值绝对值为“0”表示两个指标对其上级指标同样重要，標度为1;“0.05～0.1”表示两个指标相比，一个比另一个稍微重要，标度为3：“0.15～0.2”表示两个指标相比，一个比另一个明显重要，标度为5;“0.25～0.3”表示两个指标相比，一个比另一个强烈重要，标度为7;“大于0.35”表示两个指标相比.一个比另一个极端重要，标度为9。此外，标度2表示介于标度1和3之间的重要性，标度4、6和8表示类似含义。具体标准如表5所示。

2.3融合面板数据模型和层次分析法的新权重测算

基于表4所示混合模型拟合出的8个具体指标得分与高校综合质量得分之间的回归系数大小，测算出各指标两两之间的绝对值，与表5所示新建立的1～9标度进行匹配，建立4个判断矩阵：评估目标（0）及其一级指标（A）矩阵O-A、一级指标A，及其二级指标矩阵A-B、一级指标A，及其二级指标矩阵A-C、一级指标A，及其二级指标矩阵A-D。其中矩阵0-A建立过程中，评估目标（O）的3个一级指标A1～A3的回归系数由其子指标系数求和所得。然后对4个判断矩阵进行一致性检验，并应用“和积法”计算指标权重。一致性检验标准为CR值，当CR的值小于0.1时，判断矩阵具有令人满意的一致性。CR=CI/RI，其中CI为一致性指标，等于（最大特征根一阶数）/（阶数一1），RI为矩阵阶数对应的值（查表可得）。

基于4个判断矩阵O-A、A1-B、A2-C和A3一D计算出各指标的权重，以及4个判断矩阵的一致性检验标准CR。结果显示4个判断矩阵的CR分别为0.047、0、0.045和0，全部小于0.1，符合一致性检验标准。其中表6和表7展示了判断矩阵O-A和A1-B的指标权重及一致性检验结果，其中矩阵A-B中的数字7表示指标B，比B，强烈重要（从两个指标系数绝对值差0.278可以判断）。表8展示了各层指标权重相对于评估目标（O）的层次总排序，得到8个具体指标对于评估目标的重要性，即指标的最终权重。其中B，和B，的最终权重由B1和B2权重分别乘以A1权重所得;C1～C4最终权重由C1～C4各自权重分别乘以A2权重。

2.4融合原始权重的层次分析权重

依据表1所示各指標的原始权重，判断指标之间的相对重要性，构建4个判断矩阵O-A、A1-B、A2-C和A3-D。其中A2和A3一级指标下的C1、C2、C3、C4和D1、D2、D3权重一样，因此其权重分别是上一级权重的1/4和1/3，故不建立相应矩阵进行计算。其中表9展示了判断矩阵O-A的指标权重及一致性检验结果。表10展示了各层指标权重相对于评估目标（O）的层次总排序，即指标的最终权重。具体计算过程和方法与2.3部分相同。

2.5新权重与原始权重之间的比较分析

基于2017年中国最好大学评价指标体系各层指标的原始权重，通过两两比较各层指标的相对重要性（通过原始权重差值比较），建立相应的判断矩阵，测算出基于原始权重的新权重。表11比较分析了所选8个指标的原始权重（记为权重1）、融合原始权重的层次分析权重（权重2）、融合面板数据模型的层次分析权重（权重3）。

从表11可以看出，在一级指标A1～A3权重方面.权重1和权重2的指标权重大小不一样，但权重排序仍然一样，A1“人才培养”仍然排第一，A3“服务社会”排第三，然而基于面板模型测算的权重3中，A2“科学研究”的权重排第一。在二级指标权重方面，3类权重中排名第一仍然是B1指标“生源质量”。权重2是基于原始权重1的层次分析权重，两类权重的指标值差异相对较小，C1～C4和D1～D2权重值各自相等，无差异。权重3是基于高校各指标面板数据拟合分析结果的基础上进行层次分析得到的新权重，各指标权重之间的差值相对较大，区分明显，较具客观性。例如：权重1中的4个指标C1～C4权重全部为10%，权重2中的4个指标C1～C4权重全部为9%，而权重3中的4个指标C1～C4权重各不相同，分别为13%、10%、7%、27%，各指标的重要程度区分明显。

3融合新型评估权重和方法的中国高校评估检验

分别运用TOPSIS法、改进型TOPSIS和灰色关联法对所选高校进行评估检验和比较分析，并与原始指标权重的评估结果进行对比分析.借此检验新型定量评估权重和方法的有效性和健壮性，同时比较分析不同评估方法和权重下高校评估结果之间的差异。

3.1基于TOPSIS法和改进型TOPSIS法的高校评估检验

1）评估对象及原始数据

评估对象及原始数据由2017年中国最好大学排名结果中的Topl00所大学及其8个评估指标数据组成。由于原始数据中存在指标值为零的高校，会影响评估结果，因此删除指标值为“0”的高校，共剩下72所高校作为评估对象（部分高水平大学会因指标值缺失未选人样本），72所高校名称及其指标数据如表12所示（部分）。

为了计量比较不同指标权重下的改进型TOP.SIS法评估结果差异，分别使用表8所示层次分析法指标权重和表13所示熵值法权重对表14标准化矩阵进行加权，形成原始标准化矩阵、层次分析法权重加权的标准化矩阵和熵值法权重加权的标准化矩阵，并测算出3类标准化矩阵下的各高校接近程度C，对所选高校进行评估排名。传统TOPSIS法排名、熵值加权的TOPSIS法排名和层次分析权重的TOPSIS法排名结果，如表16所示。

如表16所示.传统TOPSIS法排名和熵值加权的改进TOPSIS法排名结果一致性相对较高.前5名的高校名单完全一致。笔者设计的融合面板数据模型和层次分析新权重的TOPSIS法高校排名结果取得较好效果，排名结果的前5名高校与中国最好大学排名的前5名高校名次完全一致，仍然是清华大学、北京大学、浙江大学、上海交通大学和复旦大学。

3.2融合新权重的灰色关联法高校评估分析

融入表8所示基于面板数据模型和层次分析法测算出的8个指标新权重，利用灰色系统关联法对所选72所高校进行灰色关联评估排名。灰色关联评价模型的构建过程：首先建立目标特征矩阵.设有M所高校有N项评价指标，建立MxN阶目标特征值矩阵X。

在该矩阵中X（K）表示第i个高校的第K项指标值。同时从矩阵X中筛选每项指标的最优值，形成最优数列：X（K）。为了实现不同类型指标之间的比较，利用正向指标的区间值标准化式（4）对矩阵X进行规范化处理，即无量纲化。

然后利用表8所示的8个指标层次分析法权重对矩阵X进行加权.并计算分析各高校的灰色关联度，即求出每所高校的比较系列xi（露）与参考系列X（K）的绝对差：AXi（K）=X（K）-X（K），并找出其最大值Amax和最小值Amin，继而利用式（5）和式（6）计算每所高校的关联系数和关联度.其计算公式如下：

其中P值设定的目的在于调整比较环境的大小，通常取值范围在0～1之间。最后基于上述灰色关联度计算过程测算出72所高校的灰色关联度大小，并进行排名，具体排名结果如表17所示。各高校灰色关联度的具体计算过程参见书藉《信息资源评估理论与实践》。

表17所示的各高校灰色关联度越大.表示高校比较序列与参考序列之间的关系越近，其排名越靠前。可以明显看出的是，表17所列举出的灰色关联度TOP15高校与2017年中国最好大学排名的TOP15高校具有较高的一致性，其中两类排名的前6名高校名单完全一致，说明融合新权重的灰色关联评估能够取得较好的评估效果。

4结论

通过设计和实现融合面板数据模型及层次分析模型的新权重测算，实证检验和比较分析了融合新权重的各类评估方法是否具有较优的评估效果和实际应用前景，具体评估结果如表18所示。表18展示了2017年中国最好大学排名靠前72所高校中TOP20所高校的原始排名（记为排名A）、融合面板数据模型和层次分析法权重的灰色关联度排名（排名B）、融合面板数据模型和层次分析法權重的TOPSIS法排名（排名C）、融合熵值法权重的改进TOPSIS法排名（排名D）、TOPSIS法排名（排名E）、高校最大最小名次的差值F和差值G。差值F表示每所高校在排名A至排名E中的最大最小名次差值;差值G表示每所高校在排名A和排名B中的最大最小名次差值：差值H表示每所高校在排名A和排名c中的最大最小名次差值。

表18所示5种高校排名使用的数据相同，而评估方法和指标权重不同，因此具有可比性。5种排名以原始排名TOP20高校为比较标准，通过比较其他4种排名结果在高校原始排名顺序上的差异，发现不同评估方法和权重所得的高校排名之间是否具有一致性。此外，设计的4种排名方法客观性和定量化较高.均通过客观权重和客观评估方法实现。从表18可以发现一些有意义的结论：

1）总体来看，5种排名中高校最高最低名次差值的平均值相对较高，为10.84。高校排名结果会受到指标权重和评估方法的影响.基于同种指标体系和相同数据，但使用不同的评估方法和权重得到的高校排名结果之间会有所差异。综合实力越靠前的高校，基于不同评估方法和权重的排名结果吻合度越高;综合实力越靠后的高校，在5种排名结果中的吻合度越低.甚至会出现部分高校不同方法排名结果差值达到30的较大差异。

2）融合新型面板数据模型和层次分析模型权重的灰色关联度排名（排名B）和改进TOPSIS法排名（排名C）在前5名高校的排名顺序上与原始排名（排名A）完全一致;排名B与原始排名A中的TOP20所高校名次差值G的平均值仅为较低的1.15，TOP72所高校名次差值G的平均值为3.39：排名C与原始排名A中的TOP20所高校名次差值H的平均值仅为1.8，TOP72所高校名次差值H的平均值为3.64。其他两种排名——融合熵值法权重的改进TOPSIS法排名（排名D）和TOP.SIS法排名（排名E）结果之间具有较高的一致性，两类排名中的前5名高校名次顺序基本一致，TOP20所高校的名次差值平均值为1.65，TOP72所高校名次差值平均值为3.5。然而排名D和排名E与原始排名A的高校排名顺序有较大差异，例如：排名D与原始排名A的TOP20所高校名次差值平均值为3.55，TOP72所高校名次差值平均值为5.78.比排名B和原始排名A的TOP20所高校名次差值平均值1.15高出2.4，比TOP72所高校名次差值平均值3.39高出2.39。

3）5种高校排名结果的前5名高校名次差异极小，每所高校最大名次与最小名次的差值在2以内。在原始排名第6至第15名的高校名次方面，5种排名高校名次差值最大的是南开大学和北京师范大学，差值均为21。总体来说，排名A和排名B的TOP15高校名次比较接近.最高名次与最低名次的差值最大为4。而排名D和排名E的TOPl5高校名次比较接近，最高名次与最低名次的差值最大为8（仅1所高校），其他高校的差值均在4及其以下。