基于线性自抗扰控制技术的四旋翼无人机控制系统*

吴君华, 谢习华,, 李拥祺

(1.中南大学 机电工程学院 高性能复杂制造国家重点实验室,湖南 长沙 410083;2.湖南山河科技股份有限公司,湖南 株洲 412002)

0 引 言

四旋翼无人机是一种能够垂直起降、自由悬停的多旋翼直升机,具有体积小、结构简单、易于维护、机动性能好等优点,在军事、民用和科研等领域有着广泛的应用前景,近年来成为国内外研究的热点之一[1]。四旋翼无人机是一个四输入六输出的欠驱动、强耦合的非线性系统[2,3]。另外由于其动力学模型的复杂性、模型参数的不确定性和建模不精确性等问题,以及四旋翼无人机实际飞行环境的复杂性,这对设计鲁棒性强和抗干扰能力强的控制器提出了更高的要求。

对此,国内外学者针对四旋翼无人机的飞行控制问题进行了相关研究。文献[4]采用模糊比例—积分—微分(proportional-integral-differential,PID)控制方法进行控制系统设计,但控制系统的响应速度较慢,鲁棒性能和抗干扰能力相对较差。文献[5]提出一种将非线性鲁棒控制用于四旋翼无人机路径跟踪的方法,但是该控制器的模型复杂,使用起来计算量较大。文献[6]采用反步法对整个四旋翼系统进行控制,该方法适合于非线性系统,但是其鲁棒性较差,一般通过其他的方法对此进行补偿。文献[7]设计出一种比例—微分(proportional-differential,PD)控制和滑膜控制相结合的控制器,用于四旋翼无人机姿态控制,但由于滑模控制算法中含有不连续的切换项,容易造成控制输入的高频抖振,从而使系统的稳定性受到影响。

自抗扰控制[8](active disturbances rejection control,ADRC)技术是20世纪80年代由中国科学院韩京清教授在PID控制技术的基础上改进而来的,该算法继承了经典PID控制利用误差消除误差的思想,同时又结合了现代控制理论状态观测的优点,克服了PID控制的一些缺点。ADRC的最核心部分是扩张状态观测器(ESO),可以将系统的内部扰动和外部扰动看成为总的未知扰动,利用ESO进行实时估计并在控制器中给予补偿。因此,ADRC适用于四旋翼无人机难以建立精确模型、欠驱动、强耦合的非线性系统。这种自抗扰控制算法是非线性的,这就使得控制器的参数过多,在实际应用中参数难以整定。因此美国克利夫兰州立大学的高志强教授提出一种线性自抗扰控制器[9](linear ADRC,LADRC),它的参数相对于非线性自抗扰控制器大为减少,便于参数调节和算法实现。

本文针对四旋翼无人机非线性、强耦合、难以建立精确的数学模型和抗干扰能力差等问题,为位置环设计了LADRC,姿态环设计了改进的LADRC。并采用仿真实验的方法将本文提出的控制器与LADRC和PID控制器作对比,对比三种控制器的控制效果。

1 四旋翼无人机动力学模型建立

四旋翼的布局形式一般分为“X”型和“十”型两种,本文选取“X”型布局形式建立四旋翼的数学模型。定义地球惯性坐标系和机体坐标系,如图1所示。

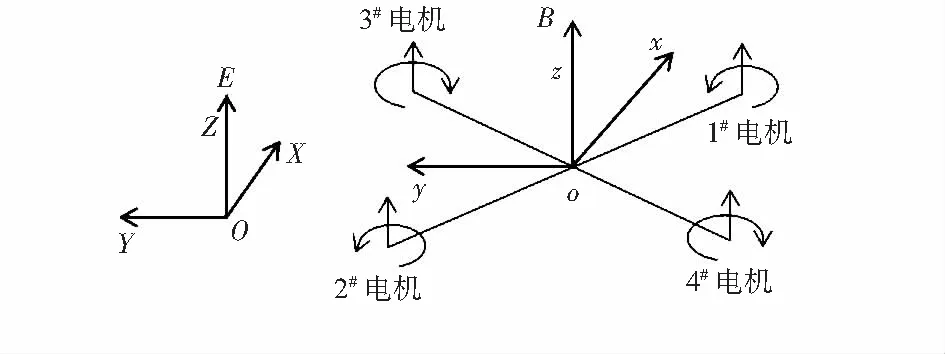
图1 地球惯性坐标系与机体坐标系示意

地球惯性坐标系E(OXYZ)相对于地面保持不动,机体坐标系B(oxyz)与无人机固联,由于四旋翼是一个近似对称的图形,其重心与质心可以看成重合在一起,故选取四旋翼的重心作为坐标原点,ox轴和oy轴分别位于1#,3#电机和2#,3#电机的角平分线上,根据右手定则oz轴垂直于oxy平面指向机体上方。

采用欧拉角表示四旋翼姿态,根据图1所建立的两个坐标系,可以确定四旋翼无人机在空中的姿态可以用机体坐标系相对于地球惯性坐标系的相对角度位置关系来表示,并可以得到从机体坐标系到地球坐标系的转换矩阵R为

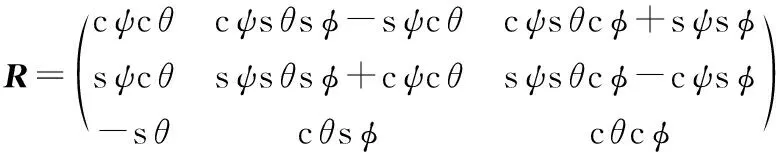
(1)

这里约定s,c和t分别代表sin,cos和tan函数。根据牛顿运动定律,四旋翼低速状态下的系统模型可表示为如下形式[10]

(2)

式中x,y,z为无人机的位置坐标。φ,θ,ψ分别为滚转角、俯仰角和偏航角。m为四旋翼无人机的质量。l为旋翼中心到机体中心的距离。Ix,Iy,Iz分别为机体绕自身x轴,y轴,z轴的转动惯量。Δx,Δy,Δz,Δφ,Δθ,Δψ分别为各个通道的未建模部分和扰动部分。四旋翼无人机非线性耦合模型分解成4个独立控制的通道,U1～U4分别为4个独立通道的控制量,其定义如下

(3)

式中F1～F4为对应电机旋转产生的升力；Ω1～Ω4为对应电机的转速；k1为旋翼的升力系数,k2为旋翼的反扭系数。

2 改进的LADRC设计

2.1 控制系统总体设计

四旋翼无人机控制系统通常分为姿态子系统和位置子系统,姿态子系统也叫做双闭环控制回路的内环,位置子系统则为外环。姿态控制是四旋翼飞行控制的基础[11],系统对内环控制的快速性和准确性要求较高,而传统的线性自抗扰可以满足一般系统的控制,所以外环采用LADRC,内环采用改进的LADRC。当控制器用作姿态控制时,外环x和y通道应为开环,内环的输入量是期望姿态角(φd,θd,ψd)和实际姿态角(φ,θ,ψ),并给定期望高度值,输出量是姿态响应的期望力(U2,U3,U4)。当控制器用作位置控制器时,外环的输入量是期望位置(xd,yd,zd)和实际位置(x,y,z),并给定偏航角度值ψd,外环输出量是期望总推力U1和期望滚转角φd和俯仰角θd。所设计的四旋翼无人机控制系统的整体框图如图2所示。

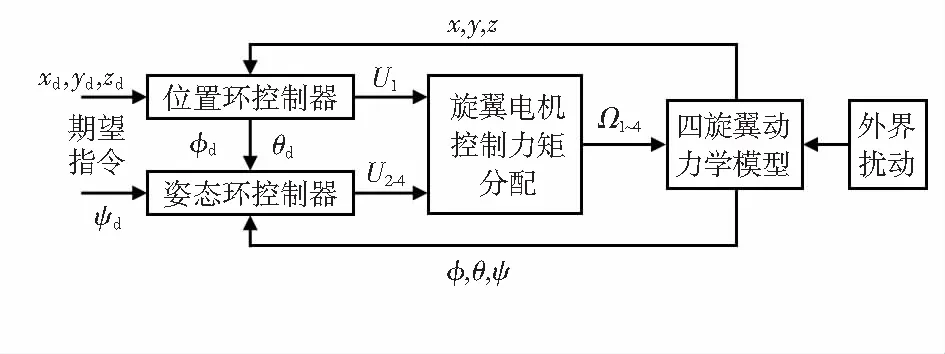
图2 四旋翼无人机飞行控制系统整体框图

由于四旋翼的控制反馈量是实时位置和姿态,不反馈电机转数,所以本文中的电机采用开环控制,根据式(3)得到各电机的期望转数(Ω1,Ω2,Ω3,Ω4),如式(4)所示

(4)

从四旋翼无人机的动力学模型可以看出,四旋翼的滚转、俯仰和偏航通道是相互耦合的,这给控制器的设计带来了很大的困难,但是ADRC可以很好地解决这一问题。各通道控制器中的ESO能观测出系统内部扰动(各通道耦合部分和未建模部分)和外部扰动当成总扰动并进行实时反馈补偿控制,从而实现各通道解耦控制,将原来非线性、强耦合的控制系统变成“积分串联”型的线性系统[12],如式(5)

(5)

式中f(·)为系统的内部扰动,Δi(i=x,y,z,φ,θ,ψ)为各个通道的外部扰动,b1=b2=b3=1/m,b4=l/Ix,b5=l/Iy,b6=1/Iz。

2.2 姿态控制

本文所设计的姿态环控制器是基于二阶的LADRC,相对于LADRC加入了Levant微分器,由Levant微分器、线性扩张状态观测器(LESO)和线性状态误差反馈(LSEF)控制率三部分组成,如图3所示,控制器结构简单,算法清晰明了。

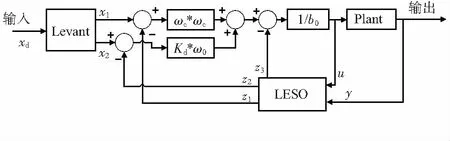
图3 改进的LADRC结构

本控制器有Levant微分器中的参数α和λ，LESO中的参数ω0和b0以及状态误差反馈补偿回路的系数Kd和ωc等6个参数需要人工整定。通过Levant微分器获得输入期望信号的跟踪信号和微分信号,实现过渡过程的配置。通过LESO扩张并估计出系统的内外扰动误差进行实时反馈补偿。其中,x1是输入期望值xd的跟踪值,x2是x1的微分值,z1是实际值y的跟踪值,z2是z1的微分值,z3是对总扰动的估计值。

以下以滚转角的控制为例说明姿态Levant-LADRC控制器的设计过程,由式(5)中的可以得到滚转角模型,并表达如下

(6)

控制算法设计如下

1)安排过渡过程

(7)

2)估计状态和总扰动

(8)

3)控制量的计算

(9)

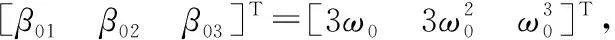
2.3 位置控制

本文所设计的位置环控制器是二阶的LADRC,其由LESO和LSEF两部分组成,控制器结构图如图4所示。控制器状态变量和参数含义同姿态环控制器一致。

(10)

期望姿态角θd,φd的求取:根据式(2)定义虚拟控制量ux,uy,uz

(11)

式中ψd为给定的偏航角度,φd和θd为所求的期望指令,由上式可得

(12)

(13)

展开上式(12)的第一行可以得到

uxcψd+uysψd=uztθd

(14)

所以有

(15)

同理展开式(12)第二行可以得到

(16)

控制算法设计如下

1)估计状态和总扰动

(17)

2)虚拟控制量的计算

(18)

y和z通道的控制器设计过程与上述类似,这里不再赘述。综上可得

(19)

3 仿真分析

为了验证所提出的改进的线性自抗扰算法的有效性和抗干扰能力,采用MATLAB软件进行数值仿真实验,将所提出的改进的LADRCC(improved LADRC,ILADRC)与LADRC以及PID控制进行对比。仿真时采用的四旋翼无人机模型的物理参数设置:m为1.5 kg,l为0.25 m,g为9.81 m/s2;Ix,Iy,Iz分别为0.013 67,0.013 37,0.024 09 kg/m2;k1,k2分别为3.1×10-7,1.12×10-7N·s2。

3.1 姿态控制仿真

分别对横滚、俯仰和偏航通道设计不同姿态跟随曲线,横滚通道跟踪矩形方波曲线,俯仰通道跟随正弦曲线,偏航通道跟随阶跃响应曲线。在姿态环加入慢时变干扰力矩Md=[2sint2cost2sint](Nm),并在8 s出加入幅值为4 Nm,宽度为0.5 s的突变干扰力矩。定义姿态角误差等于期望姿态角减去实际姿态角,仿真时间为25 s,仿真结果如图5所示。

图5 姿态控制仿真结果

从图5(a),(c)的阶跃指令变化处可以看出LADRC和ILADRC的响应时间要快于经典PID控制,超调量小,而且ILARDC要比LADRC的响应时间更快,超调量更小,这是由于ILADRC中加入了Levant微分器,Levant微分器能加快系统的响应速度的同时还抑制了系统的超调量,这就很好地解决了PID控制中快速性和超调量大之间的矛盾。从图5可以看出,经典PID控制在干扰环境下的抗干扰能力很差,在添加慢时变干扰的情况下,横滚和俯仰方向上的姿态角度误差在-2°～2°之间(不考虑信号指令在阶跃处的瞬时误差),偏航角误差在-6°～6°之间,而LADRC和ILADRC的姿态角误差均在-1°～1°之间,并且从图5(d)～图5(f)中还可以看出,ILADRC的跟随误差更小。在8s出现突变干扰处,从图5可以看出经典PID控制的姿态角出现了较大的跳变,而ILADRC和LADRC出现的跳变都很小,且ILADRC出现的跳变更小。

以上仿真结果表明ILADRC和LADRC与PID控制相比具有更好的抗扰动性能,整个系统具有更好的鲁棒性,且ILADRC的控制性能也要更优于LADRC。

3.2 位置控制仿真

根据式(2)可以看出,位置控制包含姿态控制,姿态仿真结果表明ILADRC的性能要更优于LADRC,所以姿态环选用ILADRC。为了进一步验证本控制器的控制效果,在位置环控制通道输入爬升螺旋曲线,轨迹指令为Xd=2sin(0.5t)(m),Yd=2cos(0.5t)(m),Zd=2t(m),并在姿态环中加入正弦变化的干扰力矩Md=[0.1sint0.1cost0.1sint](Nm),在位置环的x和y方向加入正弦变化的干扰力,在竖直z方向加入线性变化的干扰力(考虑到无人机在作业过程中重量会发生改变,如植保农药喷洒,油量减少),位置环干扰F=[3sint3cost5-0.3t](N)。定义位置误差等于期望位置减去实际位置,仿真时间为30 s,仿真结果如图6所示。

图6 位置控制仿真结果

从图6(b)～(d)中可以看出ILADRC和LADRC的响应速度要快于PID控制,超调量小。从图6(b),(c)中可以看出,位置环中加入水平力干扰的情况下,在系统稳定时ILADRC和LADRC的跟随误差均在-0.04～0.04 m之间,而PID控制的跟随误差在-0.2～0.2 m之间。在高度方向上存在负载变化时,ILADRC和LADRC在2s后趋于稳定,跟随误差几乎为0,而传统PID控制的跟随误差较大。这表明在位置环控制中ILADRC和LADRC的控制效果要明显优于传统PID控制,具有更强的抗扰动能力。从图6可以看出ILADRC和LADRC的控制曲线基本重合(ILADRC超调量略微小于LADRC),这是因为位置环给定的期望指令一般是连续渐进变化的,传统的LADRC也能起到很好地跟踪效果,在LADRC中引入Levant微分器在跟踪性能和抗扰动性能方面不但没有起到显著性的改善,反而增加所需人工整定的参数,这增加了算法应用于实际工程中的难度。综合以上结果将LADRC应用于四旋翼无人机的位置控制更符合实际工程的需求。

4 结 论

针对四旋翼无人机在使用传统PID控制时抗扰动性能差的问题,本文提出了一种改进的二阶线性自抗扰算法,其中位置环采用LADRC,姿态环采用ILADRC。所设计的控制器能够很好地实现姿态和位置的解耦控制,并能观测出系统的内部扰动和外部扰动进行实时反馈补偿控制,提高了系统的抗扰动能力,整个系统也具有更好的鲁棒性。

在姿态控制中,仿真实验证明了本文提出的ILADRC算法和LADRC算法在抗扰动性能和系统响应快速性方面要优于经典的PID控制,且ILADRC算法的系统响应速度与LADRC算法相比得到较大提高,抗扰动能力也得到一定的增强。

在位置控制中,LADRC和ILADRC都能实现对无人机良好控制,但LADRC更符合实际工程的应用需求。