均质细杆在纯滚动圆环内的运动

王树平

（河北建筑工程学院数理系，河北 张家口 075000）

文献［1-2］分析了质点在可自由移动的圆弧形凹槽上的运动，文献［3］对在光滑水平面上可自由移动的圆弧形凹槽内作纯滚动的圆柱体的运动进行了分析.以上文献中的两个运动物体所组成的系统都是动量守恒的保守系统.本文将对在粗糙水平面上可纯滚动的圆环内的均质细杆的运动进行分析，导出了细杆的质心在惯性参考系中的运动轨迹方程和系统的运动微分方程；求出了圆环内的细杆微振动的周期，在此基础上，分别得到了细杆在静止的圆环内以及细杆在可自由移动的圆环内微振动的周期，质点在可作纯滚动的圆环内以及质点在静止不动圆环内微振动的周期.

如图1所示，在足够粗糙的水平面上置一质量为m1，径为R的均质圆环，而在圆环内有一质量为m2，长度为l（l＜2R）的均质细杆，初始时刻，二者中心连线OC与竖直方向夹角为θ0，均质细杆由静止开始相对圆环滑动（杆与环之间无摩擦力），由于细杆的运动，圆环由静止开始相对于地面作纯滚动.

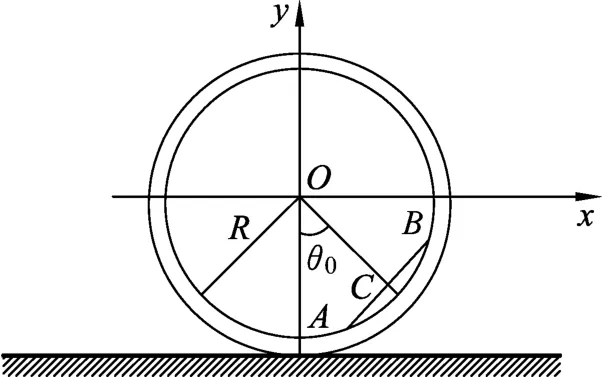
图1 初始时刻的细杆和圆环

为了讨论方便，首先建立坐标系，如图1和图2所示.以初始时刻圆环的中心为坐标原点O，Ox轴水平向右，Oy轴竖直向上，建立静止的惯性参照坐标系Oxy；然后，以任意时刻圆环的中心为坐标原点O，Ox轴水平向右，Oy轴竖直向上，建立平动坐标系Oxy.对本系统而言，有两个自由度，选O点的水平坐标x及OC连线与竖直向下的方向的夹角θ为广义坐标.

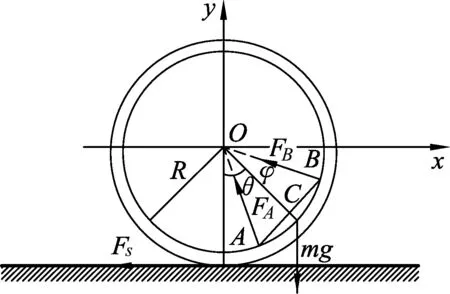
图2 细杆的受力分析

1 均质细杆的质心运动轨迹

对圆环和均质细杆的运动分析如下.圆环作平面运动，质心O的速度为，转动的角速度为，角加速度为；均质细杆也作平面运动，它的质心C作复合运动，牵连运动为随同基点O的平动，牵连速度为，相对运动为绕基点O点的圆周运动，相对速度vr=.绝对速度的平方为

2 系统的运动微分方程的建立

3 细杆在圆环内微振动的周期

4 讨论

4.1 细杆在静止的圆环内微振动的周期

众所周知，当m1≫m2，即圆环质量远远大于细杆的质量，这时，圆环可看作静止不动，于是由式（26）得到杆在静止的圆环内微振动的周期为

4.2 细杆在位于光滑水平面上的圆环内做微振动的周期

其他已知条件不变，当圆环放在光滑水平面上时，其不受水平面的摩擦力作用，也就是没有使圆环由静止转动起来的力矩，于是伴随着细杆在环内的运动，圆环只能在水平面上纯滑动，这时，用与上述相同的思路和方法容易得到，细杆在位于光滑水平面上的圆环内微振动的周期为

4.3 质点在可作纯滚动的圆环内微振动的周期

当R≫l时，即圆环半径远远大于细杆的长度时，这时细杆可看成质点，于是由式（26）得到一个质点在可作纯滚动的圆环内微振动的周期为

4.4 质点在静止不动圆环内微振动的周期

当m1≫m2并且R≫l，由式（26）得到一个质点在静止不动圆环内微振动的周期为

这是我们熟知的结论.