蚁群算法在高分子聚合与加工过程中的应用进展
蒋 波,蔡飞鹏,秦显忠,王 波,姜桂林,高金华
(齐鲁工业大学(山东省科学院),山东省科学院能源研究所,济南250014)
仿生学是一门研究自然界中生物体结构与功能,并将其应用于科技创新领域的一门科学,是人类向大自然学习的过程。在这一过程中,研究者发现了许多解决复杂问题的新方法,如蚁群算法、遗传算法和粒子群算法等[1-10]。这些以生物学特性为基础的算法在众多领域中都有广泛的应用。
蚁群算法(Ant Colony Algorithm)是一种基于群智能理论的优化算法,通过对蚂蚁觅食过程中发现路径的行为模拟,提出的一种用来寻找优化路径的概率型算法,它是由意大利学者DORIGO等于1991年首先提出,并成功用于解决旅行商问题(TSP)[11]。随着蚁群算法的普及,在解决指派问题、调度问题、图形着色、路径优化、数据挖掘、聚类分析、网络配置和序列求序等问题时也有着优秀的表现,广泛应用于解决电力、通信、化工、交通、机器人、冶金等行业问题[12-14]。
近些年,蚁群算法在高分子材料聚合与加工领域的应用越来越广泛。本文介绍蚁群算法基本原理的基础上,总结蚁群算法在高分子聚合与加工领域的国内外研究进展,并对该领域未来的发展方向进行展望。
1 蚁群算法
1.1 原 理
蚁群算法是一种新型的群智能理论优化算法,蚂蚁觅食过程中之所以总能找到食物和蚁穴的最短路径,是因为蚂蚁个体之间通过一种“信息素”的物质进行信息传递。蚂蚁在寻找食物过程中会通过释放“信息素”来标识自己的行走路径。在初始阶段,路径上没有信息素,蚂蚁的行走是随机的,随着蚂蚁不断释放信息素,越短的路径蚂蚁释放的信息素浓度越多,选择该路径的蚂蚁个数也越来越多,于是整个蚁群在正反馈的作用下集中到最佳路径上。蚁群算法具有适应性好、鲁棒性强、具有正反馈的特点。
蚁群算法的原理可以用图1来描述。
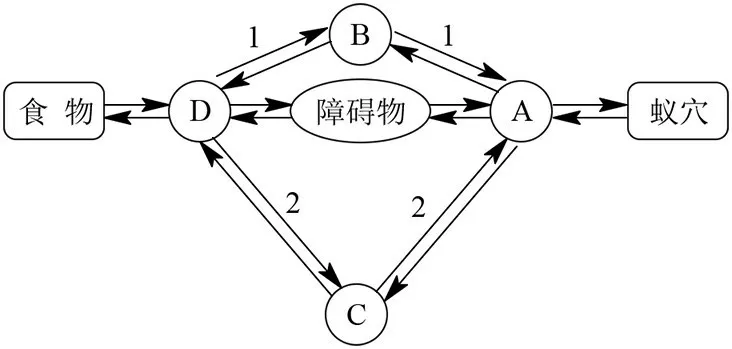
图 1蚁群算法原理Fig1 Ant colony algorithm principle
假设从蚁穴到食物之间的路径有2条,蚁穴→ABD→食物和蚁穴→ACD→食物,长度l分别是4和6,蚂蚁在单位时间内可以移动1个长度,初始时路径上信息素含量为0。当t=0时,第1组20只蚂蚁从蚁穴出发到达A点,以相同的概率各有10只蚂蚁选择路径1和2;当t=4时,第1组10只发现食物的蚂蚁返回,第2组蚂蚁到达CD中点处;当t=5时,2组蚂蚁在D点相遇,因为各有10只蚂蚁选择了1和2路径,BD和CD上的信息素数量相同,第1组返回时各有5只蚂蚁选择1和2,第2组蚂蚁向食物移动;当t=8时,前5只蚂蚁返回蚁穴,在AC和CD中点以及B点各有5只蚂蚁;当t=9时,前5只蚂蚁又回到A点并再次面临选择1和2的问题,此时AB和AC的信息素含量不同,l(AB)为20,l(AC)为15,所以多数蚂蚁选择路径1,随着时间的推移,路径1和2上信息素含量差越来越多,最终绝大多数蚂蚁选择距离短的路径1。
1.2 优化步骤
以最短路径优化为例,说明蚁群算法的优化步骤[11]。
1)参数初始化。包括蚂蚁数量m、信息素重要程度因子α、启发函数重要程度因子β、信息素蒸发因子ρ、信息素释放总量Q、最大迭代次数Iterm。
2)构建解空间。将各个蚂蚁随机置于不同出发点,对每个蚂蚁k(k=1、2、3、…m),按照式(1)计算其下一个到达地点,直到所有蚂蚁访问完所有地点。
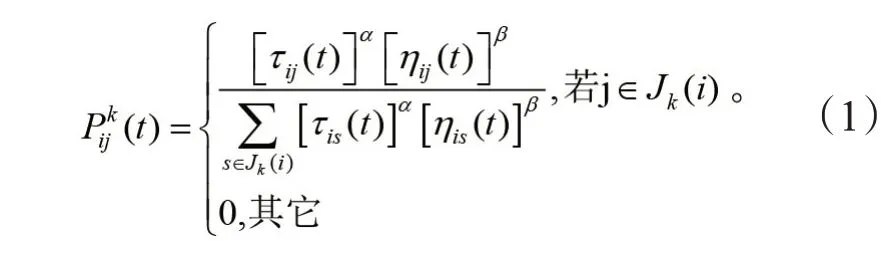
3)更新信息素。计算每个蚂蚁经过的路径长度Lk(k=1、2、3、…m),记录当前迭代次数中的最优解。同时,根据式(2)和(3)对各个地点连接路径上信息素含量进行更新。

4)判断是否终止。若iter<iterm,则令iter=iter+1,清空蚂蚁经过路径的记录表,并返回步骤2;否则,终止计算,输出最优解。
2 在高分子聚合与加工中的应用
在高分子聚合与加工领域,蚁群算法的应用越来越广泛,从单体聚合到高分子材料改性,再到高分子产品加工和复合材料优化设计等领域都有蚁群算法的应用。
2.1 聚合过程
蚁群算法在单体聚合过程、聚合反应器优化等领域有众多应用。
郭相坤等采用蚁群算法对丙烯酸酯共聚乳液配比进行了仿生优化,以乳液聚合单体配料成本最低为目标函数,采用MATLAB语言建立乳液聚合单体配料的数学模型,约束条件为聚合物玻璃化温度约束、单体约束、总量约束、库存约束以及每种参与聚合的单体用量非负约束等,结果表明,在保证玻璃化温度满足要求的条件下,每吨乳液成本比原手工配比方法节约了52.78元,按每天生产5 t计算,每月可以节约7 917元,而且优化前后乳液玻璃化温度接近,分别是317.95 K和320.97 K[15]。
随后,他们又将这一方法用于苯乙烯间歇聚合反应过程的多目标优化中,采用Visual Basic语言建立模型,优化的目标函数是:单体转化率最大、引发剂含量和残留量最低,约束条件是平均质均相对分子质量大于50×103,多分散指数在2~3。结果表明。这一方法可以得到优化的聚合过程操作参数:引发剂浓度在7.96~1.04×10-3mmol/L、引发剂残留量在0.0292~5.60μmol/L时,单体转化率在54.96%~69.98%,多分散指数在2.47~2.30[16]。表明蚁群算法可以很好的用于聚合反应过程的多目标优化。
2.2 挤出过程
TEIXEIRA等采用多目标蚁群算法对挤出机螺杆元件配置问题(TSCP)进行优化,并与遗传算法(GA)和两阶段局部搜索算法(TPLS)进行了对比。首先确定了16组螺杆元件,包含不同长度的输送元件(20、30、45、60 mm),反向螺纹元件和不同角度的捏合块(-30°、45°、-60°),通过不同算法对这些元件在螺杆轴上的排列进行优化,以最大化平均应变、最小能耗和最小粘性耗散为目标函数,约束条件是前2个元件必须为熔体输送元件,初始条件为蚁群数量30个,信息素蒸发速率0.2。结果发现,经过蚁群算法优化的螺杆元件配置,最大应变和最小能耗组合目标函数为0.950 2,遗传算法的为0.942 1,蚁群算法在处理TSCP问题中体现出巨大潜力[17]。在此基础上,他们又将蚁群算法、遗传算法、帕累托局部搜索算法、两阶段局部搜索算法等不同方法以及他们的组合应用于挤出机螺杆元件配置问题的优化,发现将帕累托局部搜索与多目标蚁群优化方法相结合是处理该问题的最佳手段[18]。
2.3 注塑过程
在注塑过程中,材料本身的特性以及复杂的加工条件使得高分子材料成形是一个影响因素多、非线性强的优化问题。蚁群算法无论在注塑工艺优化、注塑过程控制等方面都有广泛应用。
2.3.1 注塑工艺优化
黄风立等提出1种基于神经网络及蚁群算法的注塑成形工艺优化方法,对聚丙烯为原料的控制器外壳注塑过程进行了优化,以外壳翘曲形变量最小为优化函数,蚁群算法设置参数为:蚁群数20、迭代次数200、蚂蚁更新信息素常数ω=0.1、初始化信息素τ=0.5、最大残留信息素τmax=0.9、最小残留信息素τmin=0.1,发现利用交叉变异蚁群算法的求解结果优于自适应蚁群算法求解的结果,两者的最大翘曲均值分别为0.226 8 mm和0.228 8 mm[19-20]。
黄风立等基于综合关联度、Kriging模型及自适应遗传-蚁群算法提出了一种注塑成型工艺参数优化方法,对聚丙烯塑料杯的注塑过程进行优化,以体积收缩率和最小翘曲量为为优化函数。结果发现,翘曲量为0.16 19 mm,体积收缩率为0.103 3时,优化的工艺参数为:模具温度25.25℃,保压时间9.00 s,熔体温度为203.9℃,注射时间为1.01 s,利用优化的工艺参数进行实际注塑实验,测量得到最大变形量为0.181 0 mm,误差为8.25%[21-22]。
2.3.2 注塑过程控制
黄风立等基于可拓关联变量筛选、移动最小二乘及蚁群优化设计方法并考虑了随机波动因素的影响,对注塑机浇注系统进行优化设计,以最小翘曲量为为优化函数。当采用一模四件的型腔布局、标准模架、浇口在塑件长度方向的中间处时,发现利用改进的蚁群算法进行优化得到分流道直径为6.049 mm,主流道小端直径为3.085 mm,最大翘曲变形为0.255 mm,与实际注塑结果符合良好[23]。
罗海波等基于蚁群算法和混沌算法对注塑过程中PID反馈控制参数快速选取问题进行了优化,以控制误差最小为优化函数。结果发现,输出控制能在1 s内满足误差要求,以质量为30 g的制品进行实际验证,发现螺杆的注塑位置最大为32.2 mm,复位位置最大为81.2 mm,误差都在0.6%以内[24]。该算法使系统的控制效果更加优良,大大减小了系统的超调量和调整时间。
姜思佳等基于遗传算法修正的蚁群算法(GAAS)对闭环全电动注塑机PID的控制参数进行优化,以调节时间和超调量最小为优化函数。结果发现,与独立蚁群算法相比,GAAS算法的调节时间缩短了将近五分之一,超调量减小了一半[25]。在实际运行中,以MATLAB软件进行实验验证,注射螺杆的控制精度在0.5%以内,极大提升了系统的快速响应性和鲁棒性。
2.4 材料复合
玻纤或者碳纤维增强的热固性复合材料(如环氧树脂和不饱和聚酯等)具有强度高、耐弯曲和扭曲能力强、耐刮擦,在飞行器、轨道交通领域应用广泛。研究者采用蚁群算法对这类复合材料的结构、性能、成本等诸多方面进行了优化研究,取得了良好的效果。
HU等基于蚁群算法提出了1种针对复合材料及结构进行非线性优化的多尺度分析框架。首先,开发了1种能够在多尺度上对设计空间进行统一采样的方法,使蚁群算法更加完善,从而获得了优异的采样性能;其次,通过映射代表性体积元网格代替几何非结构网格,可以省去灵敏度分析;采用多级优化过程,充分利用了尺度间的弱耦合优势,使得这种分析框架可以在个人电脑上运行,当处理一般复合材料结构优化问题时,计算时间小于24 h[26]。后来AKMARC等又对该框架进行了完善,使其可以用于混合层压复合材料的多尺度和多目标优化问题[27]。
HU和AKMARC等提出的基于蚁群算法的复合材料优化框架为其他研究者的研究提供了重要的指导和借鉴。
2.4.1 结构优化
以蚁群算法对复合材料结构进行优化的研究多集中于多层层压板堆叠次序、纤维取向优化等方面,以SEBAEY和HUDSON等的研究最为系统。
SEBAEY等基于蚁群算法对多层碳纤维-环氧树脂复合材料中纤维铺放角度进行优化,以提高材料强度和抗扭曲性。优化初始条件为蚂蚁数量50,信息素蒸发速率0.05,纤维层数48,双轴向拉伸和轴向压缩载荷分别是175 N和87.5 N,允许应变0.015,蚁群算法每一条路径对应一个堆叠序列。结果发现,在双轴压缩测试中,使用常规和分散铺放角度制备的复合材料结果差别显著,使用分散铺放时,材料扭曲载荷较高,在0.12、025、0.5载荷率下,分散铺放材料可承受的最大载荷比常规铺放材料分别增加2.5%、6.3%、8%;在双轴拉伸试验中,研究了铺放方式对基体开裂破坏指数的影响,当载荷率为1时,该指数降低了20%。表明通过蚁群算法对复合材料纤维铺放角度的优化,可以显著改善材料的强度,提高抗扭曲性[28-29]。随后他们又将这一方法应用于优化碳纤维/环氧树脂复合材料结构,显著提高了材料的抗冲击性能[30-31]。
HUDSON和BLOOMFIELD等基于蚁群算法对多层取向纤维增强聚合物层压板进行结构优化,并与粒子群和模拟退火算法进行对比,在优化过程中约束条件为层压板厚度50 mm,载荷6 kN/m2且均匀分布,跨度550 mm,面层厚度0.25~5.00 mm,最大允许挠度2 mm,最大导热系数50 mW/(m·K),以层压板单位质量抗弯刚度Dm最大化以及单位成本抗弯刚度Dc最大化为目标。蚁群算法初始条件为蚂蚁数量20,信息素蒸发速率0~0.8。结果表明,蚁群算法在单位质量抗弯刚度和单位成本抗弯刚度最大化方面比其它2种方法更具优势,而且蚁群算法完成10个模拟运算的时间为111 s,模拟退火则需要11 h,而粒子群算法更是高达24 h,蚁群算法表现出更高效的运算能力[32-34]。
WEI等基于蚁群算法对折叠式无人飞机的柔性复合机翼蒙皮的蜂窝夹层结构进行优化,提高了蒙皮强度,以柔性支撑结构体积、z方向位移和总应变能最小化为优化目标,发现在迭代36次后结果趋于收敛,折叠式柔性蒙皮比强度为1.682,第1层厚度为0.25 mm,复合材料从翼根到翼尖保持0度。在优化的结构下,保持静载荷30 s过程中,翼尖左翼和右翼的变形分别为116.02和105.36 mm,均未超过给定的180 mm,完全除去测试载荷后,柔性机翼回到初始状态[35]。结果表明蚁群算法在无人机机翼结构优化方面具有优异的表现。
MANAN等基于二进制遗传算法、连续遗传算法、粒子群优化和蚁群算法对3层纤维增强环氧树脂复合材料堆叠方向进行了优化,以这种材料制造的机翼颤振和发散速度最大化为优化目标。采用蚁群算法进行优化时,最大迭代次数100,每个复合层是每个蚂蚁必须经过路径上的一个点,在每个路径点之间可以采取许多路径,以表示每1层可能的方向。结果表明,蚁群算法的优化结果最佳,标准偏差最低,3层纤维堆叠方向分别为-33.75°、45.00°、67.50°时目标函数为优[36]。但是蚁群算法的迭代次数比遗传算法多2.5倍,计算时间比粒子群优化多30%。
ABACHIZADEH等基于蚁群优化算法对对称混合层压板进行了优化,以成本最小化为目标,设计变量是表面层和芯层的数量以及纤维取向。针对纵横比和层数不同的碳纤维/玻纤/环氧树脂层压板,最终计算出了8层、16层和28层层压板的表面/芯层数以及最佳的堆叠顺序[37]。
SOUSA等基于蚁群优化算法对碳纤维增强环氧树脂复合材料AS4/3501-6进行优化设计和结构敏感性分析,通过对每层的取向角和堆叠顺序的优化实现复合材料的最优结构,约束条件是最大位移不超过1.0 mm。结果表明当层数为16时材料性能、标准偏差符合要求[38]。
WANG等基于蚁群优化算法对碳纤维-环氧树脂复合板IM7 Hexply8552-7中加强肋对板材最大扭曲载荷的影响进行了计算,通过优化蒙皮和加强肋的厚度和高度,使复合板的抗扭曲载荷性能最大,约束条件为重量小于等于4 kg。结果表明复合板的最大抗扭曲载荷能力随加强肋数量的增加而增加,当加强肋的数量从4增加到13时,抗扭曲载荷能力从80.52增加到205.78,但是当加强肋数量超过9时,数扭曲载荷增加幅度逐渐减低,而且通过优化层压板堆叠顺序,还可以进一步提高抗扭曲性能[39-40]。
2.4.2 性能优化
与复合材料结构优化相比,基于蚁群算法性能优化的研究不多,主要集中在材料导电性能领域。
KAUR等基于遗传算法和蚁群算法对导电共聚物进行结构设计,以共聚物导电性能最大为优化函数,也就是带隙最小、电子离域最大为目标,优化共聚物中不同单体的组成。优化时初始聚合物链有300个单体,网格尺寸为0.001,蚂蚁数量为50,最大迭代步数100,以Fortran语言进行计算。他们研究了2种共聚物体系:体系1中均聚物的能带宽度相差1 eV,体系2中组成共聚物的A和C聚合物能带宽度相差1.5 eV,B和C相差2.0 eV,A和B相差3.5 eV。结果发现在2种体系中,遗传算法和蚁群算法计算结果类似,在体系1中A1B1C98结构能带宽度3.5006 eV,在体系2中A98B1C1和A96B2C2能带宽度都是1.5003 eV,这些结构的共聚物均满足带隙最小、电子离域最大的目标,但是蚁群算法比遗传算法搜索时间少3%,表现出更好的优化性能[41]。
SAFER等基于蚁群优化算法,采用多层螺旋管线圈感应涡流技术对单向碳纤维增强复合材料的横向电阻率进行计算,利用蚁群算法对复合材料电阻率进行计算,将计算出的电阻率结合二维轴对称模型得到材料电阻,将计算出的电阻与实验测得的电阻进行对比,发现计算和实验测定的电阻最大误差在2%,表明蚁群算法在材料性能优化方面的可靠性[42]。
2.4.3成本优化
成本是复合材料制造过程中非常重要的因素,基于蚁群算法对复合材料成本进行优化取得了良好的效果。
HEMMATIAN等基于蚁群优化算法对玻纤/环氧树脂和碳纤-环氧树脂混合层压板质量与成本进行了优化,以质量最小化、强度最大化以及成本最低为优化目标,以混合层压板一阶固有频率大于等于25 Hz为约束条件。结果表明,与其它优化方法相比,蚁群算法在该问题的优化上效率更高。优化结构为外层为碳纤维/环氧树脂层,内层为玻纤-环氧树脂层,形成了一种三明治型复合材料,堆叠角度在40°~60°之间时材料的一阶固有频率最大,而0或者90°的堆叠角度有利于降低成本和重量,优化结构的成本因子为9.375,质量因子为5.44285,第1固有频率25.000 6 Hz[43-44]。
KOIDE等基于蚁群优化算法对多层玻纤增强以及碳纤增强环氧树脂层压板进行了优化。首先对承受双轴压缩载荷的层压复合板成本进行优化,约束条件是最大质量因子不超过85。结果表明,对于60层的层压板,蚁群算法和遗传算法得出的堆叠顺序结果一致,48和52层的层压板,取向角在±45°的板层数分别为12和14时结果为优[45]。他们又研究了使临界载荷因子λc最大化时的铺层设计问题,都取得的了良好的优化效果。
KOROUZHDEH等基于蚁群优化算法提出1种复合材料成本优化方法,以成本最低为优化函数,结果表明与其它方法相比,改进的蚁群算法具有精度高、收敛速度更快的优点,优化结构可以降低32.5%的成本[46]。
2.4.4其 它
MOUSSAVIAN等基于粒子群算法、遗传算法和蚁群算法来计算复合材料准方形切口周围应力分布有效参数的优化量,针对载荷角、切口方向和钝度这3个设计变量,优化目标是切口周围应力最小。初始条件为蚂蚁数量100,最大迭代次数30,信息素蒸发速率0.05。结果发现,堆叠顺序为[30°/0°/-30°]时,通过蚁群算法获得的成本函数的最小为2.319,堆叠顺序对准方形切口周围的应力集中具有显着影响,当钝度参数不为0时,对称层压板中方形切口周围的归一化应力小于圆形孔的归一化应力[47]。
与金属材料不同,复合材料的破坏和失效特性在不同样本之间变化很大,影响因素很多,包括制造过程产生的空隙和微裂纹,微结构残余应力以及纤维排列不规则等。HU等基于蚁群算法提出了1种自适应逆向多尺度方法,通过解决随机逆多尺度问题,从复合材料宏观实验中推断微观尺度上材料本构模型参数的概率分布,用于量化微观角度不确定性因素。结果表明,通过宏观轴向张力、横向张力和剪切力测试数据,使用该方法可以识别微观尺度的力学性能,在所有验证测试中平均值误差均小于5%[48]。
TAMA等融合蚁群、遗传和粒子群算法提出了1种逆向识别复合材料弹性的方法,并用于识别碳纤/环氧树脂复合板和玻纤-环氧树脂复合板的弹性性能,结果发现误差不超过2%[49]。
2.5 其 它
MUKHERJEE等基于蚁群算法对铜离子吸附树脂的结构进行优化,约束条件包括聚合物中重复单元的数量、结构可行性,以金属离子理论吸附量与等温吸附实验结果之间的误差最小为目标函数[50]。他们列举出吸附树脂中可能含有的官能团以及官能团基本热力学参数,然后利用蚁群算法从官能团中组合结构单元形成吸附树脂,通过基团贡献法计算活度系数,利用固液吸附理论计算树脂对金属离子的吸附量。蚁群算法初始条件为蚂蚁数量40,信息素蒸发参数0.7,当迭代达到最大迭代次数(3000),或者误差小于等于1×10-6时,运算终止。结果发现,经过优化得到的树脂吸附容量高达7.3 mmol/g,是二乙烯基苯交联的聚苯乙烯商业树脂吸附容量的10倍,优化吸附树脂结构包括2个CH2基团、1个C基团、4个H+、1个SO3基团、1个O-和8个CH3基团。
HARAMI等以溶液铸膜的方法合成了聚碳酸酯(PC)/对硝基苯胺(pNA)/4A分子筛混合膜(MMM),采用蚁群优化-自适应神经模糊推理算法(ACO-ANFIS)和遗传算法(GP)估计了H2、CH4、CO2、O2和N2分子在薄膜内的扩散系数,发现ACO-ANFIS和GP的均方误差分别为0.41和0.51,虽然2种优化算法都得出了满意的结果,但是ACO-ANFIS的准确性更高[51]。
3 结 语
蚁群算法是一种仿生学优化方法,通过对蚂蚁觅食行为的模拟,成功用于解决TSP问题,在单体聚合、挤出过程中螺杆元件配置、注塑工艺优化、复合材料设计等领域有了广泛而成功的应用:通过对成本、工艺的优化,这一算法成功对乳液聚合及聚合反应进行了优化,成功应用于挤出机中各种螺纹元件的配置以及注塑过程中产品翘曲问题的优化,近些年蚁群算法在复合材料结构、性能以及成本优化方面开展了大量研究,得到了很好的效果。
笔者认为蚁群算法在如下高分子聚合与加工领域值得进行进一步研究:
1)挤出过程,挤出过程包括固体输送、熔融和均化等不同阶段,这些过程中既有物理混合也有化学反应,采用蚁群算法对上述混合、反应过程进行优化有望进一步阐明挤出过程中的诸多原理;
2)注塑过程,与挤出过程类似,这个过程影响因素多、非线性强,已有的研究多集中于注塑工艺优化及控制,针对注塑过程中的物料混合、模具填充过程的流动混合机理的研究更具有重要意义;
3)合金/共混物结构与性能优化,基于蚁群算法众多研究者对纤维增强的环氧树脂复合材料进行了广泛研究,但是对其它类型的高分子共混物以及合金的研究鲜有报道,这一方法的应用必将促进高分子材料结构和性能的优化研究。

