(K,t)-Wythoff博弈模型多项式时间的取胜策略
李海燕, 白云霄, 曹 慧
(陕西科技大学 数学与数据科学学院, 陕西 西安 710021)
0 引言
组合博弈及其取胜策略蕴含着严密的数学逻辑和深刻的理论体系,因而一直受到许多数学研究者的关注.Wythoff模型是经典的两人公平组合博弈模型之一,其取胜序列与贝蒂定理和斐波那契序列等密切相关.Wythoff模型可描述为:给定初始位置(x,y),两人轮流移动,移动规则包括(i)(x,y)→(x-k,y);(ii)(x,y)→(x,y-l);(iii)(x,y)→(x-k,y-k).终止位置为(0,0).其中x,y∈且k,l∈+.最后移动者取胜.博弈过程中双方具有相同的决策集(公平的),即双方面对某个位置或状态时具有相同的可选移动[1].
1998年,Fraenkel将上述移动规则(iii)扩展为(x,y)→(x-k,y-l),s.t.|k-l| 在公平组合博弈中,给定一个位置或状态,如果竞争者从该位置出发没有任何取胜的策略,则称该位置为P位置; 如果从该位置出发至少存在一种取胜策略,则称该位置为N位置.比如在Wythoff模型中,(0,0)、(1,2)、(3,5)等是P位置,同时,根据移动规则的对称性易知(2,1)、(5,3)等也是P位置.对于任意一个公平组合博弈模型,分别用P和N表示它的所有P位置集合和所有N位置集合,且二者划分了所有的状态集.通常P位置相对较少,因此许多学者通过研究模型P位置的特性来确定模型的取胜策略.注意组合博弈模型的取胜策略只取决于模型本身的移动规则和取胜规则.更加详细的组合博弈理论和更多有趣的组合博弈模型,可参考文献[4-8]. 其中mexS=min{S}表示除数集S中所有元素之外的最小非负整数,例如mex{0,2,3}=1.Fraenkel指出任给博弈位置(x,y)∈×,由mex函数表示P位置集合的递归形式所提供的取胜策略在算法的执行时间上关于输入规模logxy是指数的[2,9]. 给定参数K,t∈+,设Ωk={0,1,2,…,K-1},则(K,t)-Wythoff模型的P位置集合为 其中 这里|「·⎤ 表示向上取整函数,例如|「2.4⎤=3. 在文献[3]中,作者通过(K,t)-Wythoff模型与t-Wythoff模型之间的内在联系,借助于t-Wythoff模型已有的多项式时间取胜策略,间接地给出(K,t)-Wythoff模型的一种多项式时间内可计算的取胜策略.本文将基于(K,t)-Wythoff模型的两个参数和P位置特点及其数学性质,构造一个特殊的数制系统,同时模型位置在该数制系统下表示唯一且具有简洁的规律性,于是(K,t)-Wythoff 模型的取胜策略不再依赖于mex函数的递归表示形式,进而能够在多项式时间内计算. 设u-1为常数,令u0=1,且整数b1≥b2≥1,考虑线性迭代关系:un=b1un-1+b2un-2(n≥1).以u0,u1,u2,…作为权值,以di∈{0,1,…,b1}作为数码,构造数制系统,记为U.但对于正整数un此时有两种表示方法:un本身和un=b1un-1+b2un-2.因此,为保证表示唯一性,规定:当di=b1时,一定有di-1 在文献[3]中,对于t-Wythoff模型,构造数制系统U1:令u-1=u0=1,b1=t,b2=1,则un=tun-1+uu-2(n≥1),且di+1=t⟹di<1(i≥0). 例1在t-Wythoff模型中,考虑t=2的情形.此时u-1=u0=1,u1=3,u2=7,u3=17,….表1列出了正整数1至25在U1中的表示.表2列出了当t=2时t-Wythoff模型的前若干个P位置. 同时满足以上三条性质的位置(An,Bn)一定是t-Wythoff模型当t=2时的P位置. 任给t-Wythoff模型的位置(x,y),不失一般性,设0 表1 当t=0时,正整数1至20的U1表示 表2 当t=2时,t-Wythoff模型的若干P位置 定义1给定参数K,t∈+,令u-1=u0=K,线性迭代关系为: un=|「t/K⎤un-1+un-2(n≥1). (1) 以u0,u1,u2,…作为权值,以di∈{0,1,…,|「t/K⎤}作为数码,并规定di+1=|「t/K⎤⟹di=0(i≥0),定义一个新的数制系统,记为UK. 对任意的i≥0,易知ui∈Mk={nK|n∈}.集合MK中每一个元素即模K余0的非负整数N都可以在数制系统UK下表示,且表示形式唯一,记为RUk(N).数制系统U1实际上是数制系统UK当K=1时的特殊形式,因此UK是U1的推广. 例2设参数K=3,t∈{4,5,6},则|「t/K⎤=2,于是u-1=u0=3,u1=9,u2=21,u3=51,….数码di∈{0,1,2}.表3给出了集合MK中3至69的UK表示. 表3 当t=2时,集合MK中3至69的UK表示 引理设在数制系统UK的表示下,属于集合MK以偶数个0结尾的数记为{Vm}m≥0,且0=V0 Dm-Vm=|「t/K⎤Km. (2) 证明:对m进行数学归纳.当m=0时,V0=D0=0,结论成立.假设式(2)对于任意m都成立,下面只需证该等式对于m+1也成立. (3) 令r=|「t/K⎤,则UK的迭代式(1)简化为 un=run-1+un-2(n≥1), (4) 且di∈{0,1,…,r}满足di+1=r⟹di=0(i≥0).接下来分情况讨论,因为RUK(Vm)的结尾形式一定是以下三种情形之一: 情形1RUK(Vm)的结尾形式为: d2k+1d2kd2k-1…d2d1d0=d2k+1r0…r0r0r,k∈, 其中d2k+1∈{0,1,…,r}且d2k+1=0⟹d2k+2 且以奇数个0结尾; 同时Vm+2K以1结尾,即以偶数个0结尾,如图1所示. 图1 情形1中Vm+K和Vm+2K 结尾形式示意图 而Vm∈MK(m≥0),所以Vm+1=Vm+2K.注意 RUK(Dm+1)-LRUK(Vm+1),于是一方面 Dm+1-Vm+1=(u1-u0)+(d2k+1+1)u2k+2+ 另一方面,根据式(3), |「t/K⎤Km=r(u1-u0)+r(u3-u2)+ r(u5-u4)+…+r(u2k+1-u2k)+ 注意将等号右边所有正项相加,再加u0减u0,将所有负项相加,再减u-1加u-1,根据式(4),得 |「t/K⎤Km=u2k+2-u0-u2k+1+u-1+ 因此,Dm+1-Vm+1=|「t/K⎤K(m+1). 情形2RUK(Vm)的结尾形式为: d2kd2k-1d2k-2…d2d1d0=d2k0…0,k∈+. 其中d2k∈{1,…,r},而 并且Vm+K也以偶数个0结尾,如图2所示. 图2 情形2中Vm+K结尾形式示意图 故Vm+1=Vm+K.于是, 情形3RUK(Vm)的结尾处d0满足0 图3 情形3中Vm+K结尾形式示意图 由定义1可知,d1 Dm+1-Vm+1=(d0+1)(u1-u0)+ |「t/K⎤K(m+1). 证毕. 3 (K,t)-Wythoff模型多项式时间的取胜策略 定义2在(K,t)-Wythoff模型中,给定参数K,t∈+,根据其P位置集合表达式,对每一个n∈,(An,Bn)是P位置当且仅当(An+α,Bn+β)是P位置,其中α,β∈ΩK={0,1,…,K-1},我们称(An,Bn)为(K,t)-Wythoff模型的P诱导位置. 例3在(K,t)-Wythoff模型中,考虑K=3,t∈{4,5,6}的情况,表4列出了(K,t)-Wythoff模型的前若干个P诱导位置. 表4 当K=3,t∈{4,5,6}时,(K,t)-Wythoff模型的若干P诱导位置 为了陈述主要结果,这里给出(K,t)-Wythoff模型P诱导位置序列{An},{Bn}的几个重要性质[3]: 性质1An,Bn∈MK={nK|n∈,K∈+}; 性质2对任意n>m≥0,有Bn>An>Am; 下面讨论数制系统UK与(K,t)-Wythoff模型之间的联系,并通过下面的定理为(K,t)-Wythoff模型提供多项式时间的取胜策略. 定理对所有的n∈,有(Vn,Dn)=(An,Bn). 证明:当n=0时,显然有 (V0,D0)=(A0,B0)=(0,0). 对于n≥1,首先由引理和性质1可知Vn,Dn,An,Bn∈MK;其次Dn关于Vn与Bn关于An具有相同的函数关系,因此只需证An和Vn具有相同的递归表达式,即证 Vn=mex{Vi+α,Dj+β|0≤i,j S={Vi+α,Dj+β|0≤i,j 假设存在某个τ≥n,使得maxS=Dτ,既然Vτ 证毕. 定理表明,在数制系统UK的表示下,(K,t)-Wythoff模型的P诱导位置具有显著而简洁的规律: 规律1所有RUK(An)均以偶数个0结尾. 规律2所有RUK(Bn)均以奇数个0结尾. 规律3对于任意n,RUK(Bn)=LRUK(An). 借助于数制系统UK的取胜策略优点是不存在递归的形式,时间复杂度大大减小,类似于第一部分的分析,相应取胜策略在多项式时间内可计算.那么任给(K,t)-Wythoff模型的位置(x,y),如何确定它是P位置或是N位置以及相应的取胜策略?为了叙述方便,给出以下推论. 推论给定参数K,t∈+,设(x,y)为(K,t)-Wythoff模型的任意位置,则(x,y)∈P当且仅当存在n∈,使得 (|「x/K⎤K,|「y/K⎤K)=(Vn,Dn). 证明: 在(K,t)-Wythoff模型中,由于(An,Bn)∈P当且仅当(An+α,Bn+β)∈P,其中An,Bn∈MK,α,β∈ΩK.因此,(x,y)∈P当且仅当存在n∈,使得(|「x/K⎤K,|「y/K⎤K)=(An,Bn).由定理可知结论成立. 证毕. 任给(K,t)-Wythoff模型的位置(x,y),设 本文通过定义一个新的数制系统,使得(K,t)-Wythoff模型的P诱导位置在该数制系统下的表示形式唯一且规律简洁,相应的取胜策略在多项式时间内可解.因此,相对于递归形式提供的指数时间的取胜策略,在时间复杂度方面进行了改进.
1 预备知识

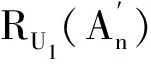



2 一个新的数制系统

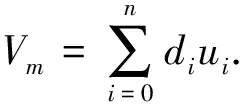



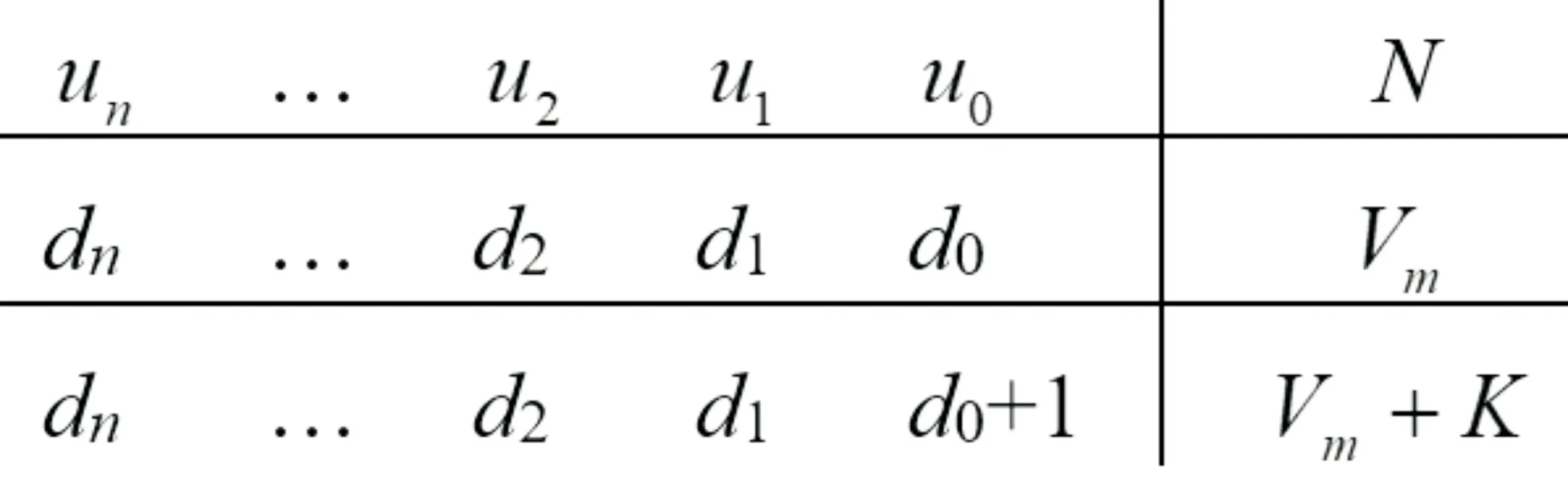


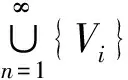



4 结论

