非理想情况下无线中继系统多域抗干扰方案
李永成,周小猛,高贞贞,3,白少壮,李康泽
(1.电子信息系统复杂电磁环境效应国家重点实验室,471003,河南洛阳;2.西安交通大学信息与通信工程学院,710049,西安;3.东南大学移动通信国家重点实验室,210096,南京)
由于无线通信具有广播特性使其易遭受干扰攻击,因此抗干扰技术的研究显得日益重要。在无线抗干扰技术的研究中,已有的研究方向主要是针对空间域、频域或者功率域。应用于卫星通信的空间域抗干扰技术[1-3]通常有空间隔离法、频率隔离法、信号处理法(扩频和跳频等)等抗干扰方案;频域的主要抗干扰技术[4-5]是扩频技术,它包括跳频技术[6]、直接序列扩频技术[7]及自适应扩频技术[8];功率域的抗干扰技术被认为是最直接有效也是使用最广的抗干扰方案,主要通过改变通信方与干扰机的发射功率来实现[9-11]。
近年来,从很多人为干扰案例可以看出通信与干扰都在向着智能化发展。博弈论可以满足通信方与干扰机进行智能化决策的需求[12-13]。例如,文献[14]提出了一种零和博弈模型,用来分析用户和干扰者之间的关系。针对通信方与干扰机之间的主从对抗特征,已有文献表明Stackelberg博弈模型非常适用于该场景。文献[6]研究了时间域的抗干扰策略,通过Stackelberg博弈模型找到通信方跳频的最优跳速,并在求解过程中考虑了观测误差造成的影响。文献[9]的作者主要研究功率域抗干扰系统,在不完全信息场景下建立Stackelberg博弈模型。文献[10]的作者梳理了各种不同情况下的无线通信抗干扰技术。文献[11]的作者主要研究了无人机通信中的抗干扰问题,考虑了观测误差和信息的不确定性。
前述工作主要针对点对点通信系统研究了基于单域的抗干扰技术。随着中继的引入,无线通信系统应用场景进一步扩展,中继可以有效地帮助用户提高通信质量。针对译码转发中继辅助抗干扰通信系统,文献[15]的作者将中继节点作为Stackelberg博弈的副领导者,建立了3层Stackelberg博弈模型。针对放大转发中继系统,文献[16]的作者提出了一种基于跳频的多域抗干扰策略,使用Stackelberg博弈来模拟通信方和干扰者之间的交互作用,但是该工作只适用于博弈双方能够获得彼此完美信息的理想情况。
基于已有研究工作基础,本文针对存在不确定信道信息和参数估计误差的非理想情况,在放大转发中继系统中提出了基于Stackelberg博弈的联合时间域和功率域的抗干扰方案。本文的博弈模型将源和中继作为领导者,干扰机作为跟随者,建立双层的Stackelberg博弈模型,然后用逆向归纳法求解通信方和干扰机的最优多域参数。仿真结果表明,本文所提多域抗干扰方案相比于已有单域方案和多域随机方案具有显著的性能优势。
1 系统模型及博弈模型建立
1.1 系统模型
考虑一个两跳的无线中继系统,系统模型如图1所示。该系统由一个源节点S、一个目的节点D、一个可信中继节点R和一个干扰节点(干扰机)J组成,中继采用放大转发协议,工作在半双工模式。由于障碍物的遮挡,源节点和目的节点之间没有直接链路。源到目的节点的传输分为两个阶段:阶段1,源节点以功率PS向中继发送信号;阶段2,中继对接收信号能量归一化并用功率PR进行信号转发。干扰机在检测到信号后会对源和中继进行干扰。用hSR、hRD、hJR、hJD来分别表示S与R、R与D、J与R以及J与D之间的信道。在D处受干扰的接收信号可以表示为[17]

图1 两跳无线中继系统模型Fig.1 System model of two-hop wireless relay
y=hRDη(hSRs+hJRsJ1+nR)+hJDsJ2+nD
(1)
式中:s表示信源S发出的信号,发射功率为PS;sJ1表示J发送到R并且功率为PJ1的零均值高斯干扰信号;sJ2表示J发送到D且功率为PJ2的零均值高斯干扰信号;nR表示R处方差为NR的零均值高斯噪声;nD表示D处方差为ND的零均值高斯噪声;η表示中继的放大转发因子,可以用下式来表示
(2)
假设源节点和中继的最大发射功率分别为PS,max和PR,max,则PS≤PS,max,PR≤PR,max。对于干扰机,假设其最大总功率为PJ,则PJ1+PJ2=PJ,功率分配系数为ρ=PJ1/PJ。
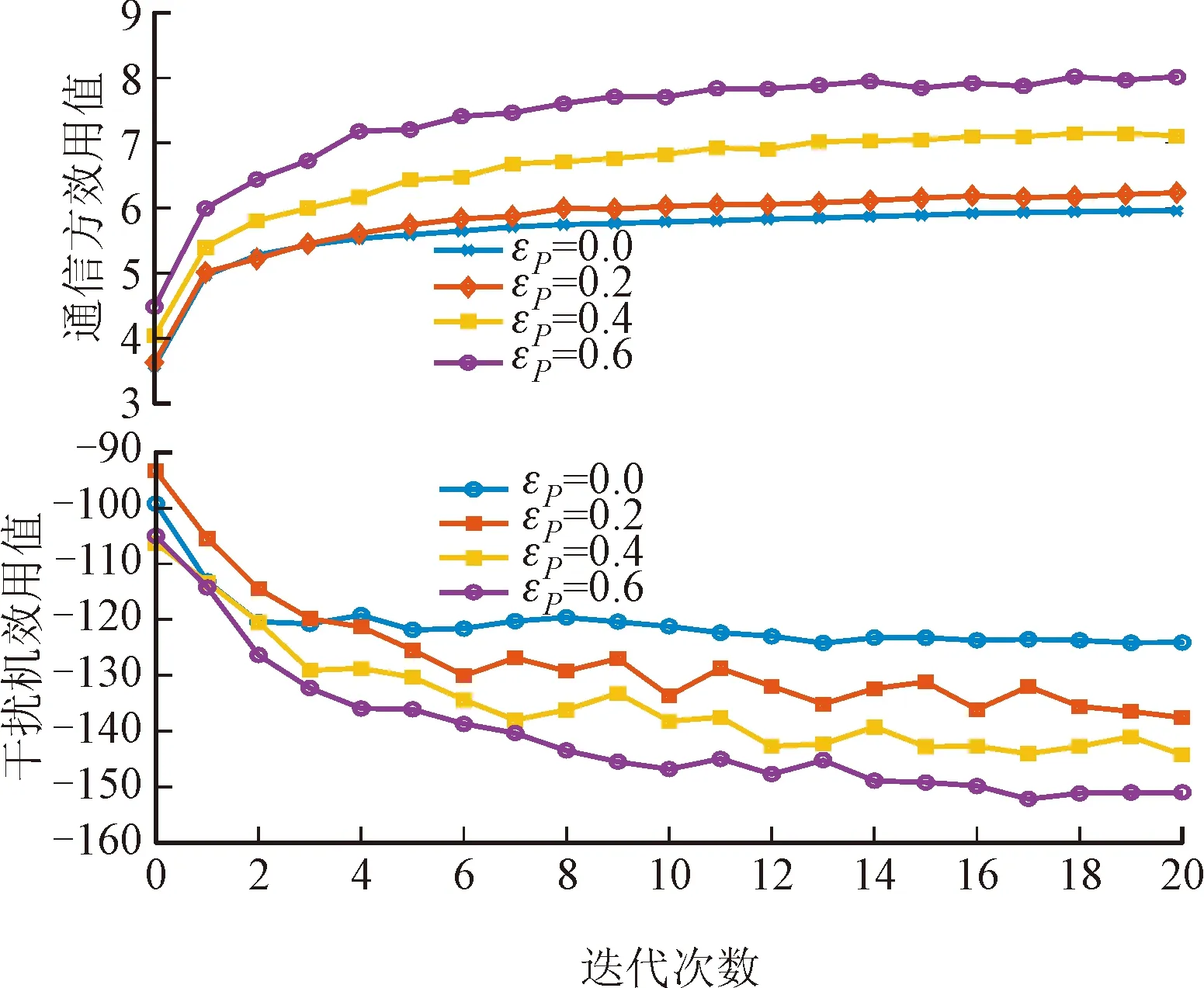
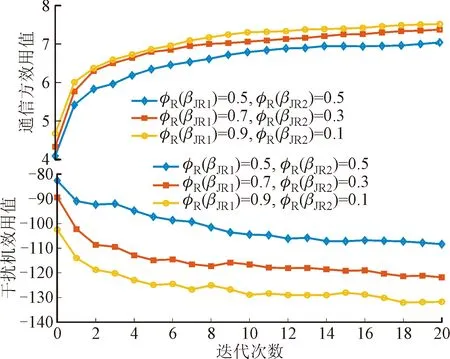
典型的跳频信号结构示意图如图2所示。干扰机采用引导式跟踪干扰的干扰策略:在每个跳频周期内,干扰机首先检测跳频信号,若检测到跳频通信信号,则立即引导干扰机进行干扰;否则,干扰机不发射干扰信号。将每个跳频周期T表示成两部分:信号检测时间TE和干扰时间TI,即T=TE+TI,其中T∈[0,Tmax],Tmax为最大跳频周期。假设T1为阶段1和阶段2的持续时间,且T=nT1,其中n为正整数。此外,将TI表示为TI=mT1,m 图2 跳频信号结构示意图Fig.2 Structure diagram of frequency hopping signal 跳频信号在M个相邻但不相交的子频带内伪随机跳变。通信方包括源和中继能够根据引导式跟踪干扰的参数,在满足最大跳频周期的范围内自适应调整跳频周期。从图2可见,干扰机检测时间越长,它能正确跟踪通信方信号的概率就越高,但是剩下用来干扰的时间就会越短。通信方能够根据干扰机的情况自适应改变跳频周期以最大化自己的利益,故干扰机的检测时间和通信方的跳频周期对通信方的性能有着重要的影响。因此,本文将时间域和功率域联合考虑,求解能最大化通信方效用函数的时间域和功率域参数。 由于信号检测概率往往与检测时间或信号发射功率有关,用pd表示跳频通信信号的检测概率,根据文献[19],pd可表示为 (3) 式中:γJ表示干扰机J处的接收信噪比。 已有工作通常假设通信方具有干扰机的完美信道状态信息,并依此来确定其最佳策略,这在实际情况下往往是不可行的。为了建模更实际的情况,本文考虑如下的非理想情况:通信方只能获得干扰信道的不确定信道信息,且干扰机和通信方对功率域及时间域参数的估计存在误差。 考虑到信道信息的不确定性,通信方没有干扰机信道增益的完美信息,但是根据文献[9],可以如假设1所示,通信方能够获取他们的概率分布。此外,如假设2所示,干扰机和通信方对对方参数的估计存在估计误差。 假设1对于通信方而言,只能获得干扰机到通信系统的不确定信道信息,假设干扰机到中继和目的节点的信道增益分别为gJR,gJD,它们分别有B和K种状态,表示为βJR,b,b=1,…,B和βJD,k,k=1,…,K。其概率分布分别为φR(βJR,b)和φD(βJD,k),则有 (4) 1.3.1 通信方效用函数 考虑到实际无线设备电池容量有限的能量限制,建立通信方的效用函数时,在衡量通信关键指标的同时也要考虑发射代价。除此之外,由于考虑了不确定信道信息和参数估计误差,我们需要对不同干扰机信道增益下的接收机的平均信干噪比依概率求和,因此将通信方的效用值定义为 CSPS-CRPR (5) (6) 由信噪比的定义得到式(6)中γD为[16] (7) 式中:gSR=κ[d0/dSR]α和dSR分别是S到R信道的增益和距离,κ是由天线特性和平均信道损耗所决定的常系数,d0是天线远场的参考距离,α是路径损耗因子;gRD=κ[d0/dRD]α和dRD分别是R到D的信道增益和距离。考虑到非理想情况,式(6)中的ΓD应写为 (8) 根据[16],通信方估计J的接收信噪比为 (9) 式中:NJ是J处的零均值高斯噪声的方差。 (10) 1.3.2 干扰机效用函数 考虑干扰机由电网供能,这对于合法通信系统来说是最坏情况。与电池供能设备相比,干扰机的发射代价可以忽略不计。因此考虑估计误差后,干扰机的效用函数表示为 (11) (12) (13) (14) 式中:Le3=[ND+(1-ρ)PJgJD];Le2=[NR+ρPJgJR]。 (15) (16) 1.3.3 基于效用函数的优化模型 根据上述效用函数,通信方和干扰机的目标是使各自的效用值最大化。根据跳频信号的检测结果,作为跟随者的干扰机从以下优化问题中确定最佳检测时间TE和功率分配系数ρ (17) 而作为领导者,信源和中继从以下优化问题中确定最佳发射功率和跳频周期 (18) 本节将采用逆向归纳法对建立的Stackelberg博弈模型进行求解。求解时,干扰机作为跟随者根据跳频信号的检测结果求解其最优检测时间和干扰功率分配因子,并推导出最优近似闭式解。通信方作为领导者使用基于遗传算法(GA)的优化方案求解其功率域和时域参数。 干扰机作为跟随者可以根据检测到的跳频信号估计通信方参数,下面将在给定通信方参数下求解最优干扰机参数。 (19) 根据文献[16],可求得闭式解为 ρ*=min(1,max(0,ρ0)) (20) 式中,ρ0所代表的多项式如下 (21) 2.1.2 最优信号检测时间 在获得最优功率分配系数后,可得到信号检测时间的最优值。根据文献[16]已经证明的结论,公式(17)可以被简化为以下等式 (22) 其中m*的表达如下 (23) (24) 式中,μ的表达式为 (25) 以信源和中继为领导着来优化PS、PR、T。采用一种基于质数分布的遗传算法(GAED)[20]来解决这一非线性双层规划问题。 2.2.2 适应度计算 对于第t代的个体,适应度函数由下式表示 (26) 式中:η表示一个充分大的正数。适应度函数后两项的存在,使得算法能够在迭代过程中让含有异常值的个体获得很低的适应度值,并在之后的迭代过程中淘汰这部分个体。 完成第t代所有个体的适应度值计算后,记录适应度最好个体为I*t=(L*t,G*t)和从t-1代遗传的所有可能个体中具有最大通信方的效用值的个体I′t=(L′t,G′t)。 (27) 式中:μ∈[0,τ],其中τ是限制因子,避免交叉过后的个体的参数在约束集之外;Qt是提供交叉方向的向量,并且基于L*t和L′t进行优化。 选择合适的Qt十分重要,因为L*t是第t代种群中适应度最好个体的通信方参数,我们希望Qt能以更高的概率接近L*t,因此本文选择了基于指数分布的选择法。假设F服从指数分布,则有 (28) (29) 2.2.5 选择 从第t代所有个体、集合O1和集合O2之中选择适应度值最高的Pn个个体作为下一代种群的一部分个体,其中Pn 本文主要仿真参数的设置参照了相关文献[6,15-16]对类似场景的仿真参数设置,设置如下:令单时隙通信周期T1为1 ms,频率切换时间T0为0.5 ms,最大跳频周期为100 ms;干扰机的发射功率为PJ=10 W;信源和中继的最大功率限制设置为PS,max=PR,max=1 W;噪声功率NJ=NR=ND=-50 dBm;可选信道数M为32。仿真采用室外场景,信源、接收机、干扰机和中继的位置坐标设置为[-4,0]、[2,0]、[0,3]及[-1,0]km;信道参数设置为κ=1,d0=0.1 km,α=3。仿真中初始种群数l为30;交叉概率pc和变异概率pm分别为0.8和0.2;信源和中继的发射功率代价因子设为CS=CR=0.8。 为了衡量不确定信道信息、功率及时间域参数估计误差对效用值的影响,我们定义了通信方和干扰机的实际效用值,即通信方和干扰机在不确定信道信息和参数估计误差的情况下进行抗干扰决策,将决策结果运用于干扰机当前真实信道及功率分配,以及通信方真实发射功率和跳频周期的情况下,计算通信方和干扰机的实际效用值,因此通信方的实际效用值可写为 (30) 图3为干扰机对参数T的估计误差对效用值的影响图,可以看到εT越大,通信方效用值越大,干扰机效用值越小。这是因为当干扰机对通信方参数存在估计误差会导致自己的参数偏离最优值,使得干扰机效用值下降,通信方效用值增大。 图3 时间域估计误差对效用值的影响Fig.3 Effect of estimation error in time domain on utility value 图4为干扰机对发射机功率参数的估计误差对效用值的影响图,令εP=εPS=εPR。可以看出,εP越大,通信方效用值越大。同样因为干扰机估计误差越大,干扰机的观察结果与实际值之间的偏差就越大,这会影响干扰机的决策并降低干扰机效用值和增加通信方效用值。 图4 功率域估计误差对效用值的影响Fig.4 Effect of estimation error in power domain on utility value 图5考察了不确定信道信息对效用值的影响,我们在不同的概率分布下进行了通信方实际效用值仿真。在图5的3种概率分布中,当φR(βJR,1)=0.5、φR(βJR,2)=0.5时,对于干扰信道状态的不确定度最大;φR(βJR,1)=0.9、φR(βJR,2)=0.1时,对信道状态的不确定度最小。由图5可得,当信道的不确定度增加时,由于通信方不能精确进行优化而导致通信方效用值下降。 图5 不确定信道信息对效用值的影响 Fig.5 Effect of incomplete channel information on utility value 假设J到R的信道增益有两个状态[βJR,1,βJR,2]=[0.2,0.3],干扰节点J到接收机D的信道增益也有两种状态[βJD,1,βJD,2]=[0.3,0.6],其分布概率为φR(βJR,1)=φR(βJR,2)=φD(βJD,1)=φD(βJD,2)=0.5。对于通信方和干扰机的估计误差,我们设置εT=εTE=εPS=εPR=0.2,ερ=0.02。 图6展示了本文所提多域博弈方案与单域博弈方案和多域随机方案的效用值对比。单域博弈方案包括单时域和单功率域,其中,在单时域方案中随机选择功率(PS,PR),通过遍历获得最优跳频周期T,最后用上文推导出的闭式解来选择最优信号检测周期TE和功率分配ρ。而单功率域方案则是相反,即盲跳频随机选择跳频周期T,遍历获得最优(PS,PR)。多域随机方案则随机选择时域和功率域参数。通过分析图6的仿真结果,可以发现多域随机方案具有最小的通信方效用值,而本文所提方案具有最大的通信方效用值。单域博弈方案中,单功率域方案能取得较高的通信方效用函数值,随着发射代价的增大,单功率域方案与本文方案的差距逐渐减小。当发射代价为CS=CR=0.7时,本文方案通信方效用值为27.43,单功率域方案通信方效用值为13.22,本文方案的通信方效用值相比于单功率域方案提高约100%,当发射代价为CS=CR=0.8时,本文方案通信方效用值为7.56,单功率域方案通信方效用值为3.36,本文方案的通信方效用值相比于单功率域方案提高约50%。与此同时,本文方案取得了最小的干扰机效用值。当发射代价为CS=CR=0.7时,本文方案的干扰机效用值约为-165,单功率域方案的干扰机效用值约为-100,本文方案的干扰机效用值相比于单功率域方案至少恶化了50%。 图6 本文方案与对比方案的效用值对比Fig.6 Comparison of utility value between the proposed scheme and the comparative schemes 本文针对存在恶意干扰机的放大转发中继系统提出了一种多域抗干扰方案。该方案使用Stackelberg博弈来建模通信方和干扰者之间的交互作用,并考虑了实际情况下对抗双方信息获取困难的问题,对不确定信道信息和功率域及时间域参数估计误差进行了建模,采用逆向归纳法对博弈双方的时域和功率域参数进行了求解。通过仿真讨论了参数估计误差和不确定信道信息对于通信方和干扰机效用值的影响,并证明了本文所提多域博弈方案相较于单域博弈方案和多域随机方案的优势。
1.2 非理想情况

1.3 Stackelberg博弈模型建立









2 基于多域的博弈抗干扰方案
2.1 跟随者干扰机的子博弈
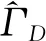

2.2 领导者通信方的子博弈






3 仿真结果分析

3.1 估计误差对效用值的影响

3.2 不确定信道信息对效用值的影响
3.3 与不同方案的对比

4 结 论

