翅片式弯头流动调整器的整流特性

邓清华,何伟,张亮,彭傲然,赵卓斌,丰镇平

(1.西安交通大学叶轮机械研究所,710049,西安;2.西安交通大学陕西省叶轮机械及动力装备工程实验室,710049,西安;3.上海核工程研究设计院有限公司,200233,上海)

均匀稳定以及不存在明显的流态畸变是能源、化工等工艺流程中旋转机械、流量测量装置对来流状态的基本要求。非均匀的来流会导致泵产生振动、气蚀、扬程降低等问题。当流量计上游流动速度剖面不对称时,至少要布置50倍管径距离的直管段来削弱流态畸变的影响[1]。然而在实际管路布置条件下,弯管、三通、孔板、扩张管等结构是非常常见的,流体流过这些结构则必然出现不对称速度分布和复杂二次流[2-3]。为了将上述流态畸变削弱到满足泵或流量计要求的范围,同时避免占用大量物理空间和增加系统成本,一般采用流动调整器装置而不是铺设几十倍乃至上百倍管径长的直管段。按照结构的不同,流动调整器分为叶片式、管束式、格栅式、孔板式、翅片式等[4-6]。

叶片式流动调整器的典型代表是Etoile式流动调整器[6],其采用八个周向分布的叶片将流动空间分为均匀的扇形部分[7],优点是易加工、结构简单、压力损失低,但整流效果一般。Laws等研究发现,较短的长度和空心设计能够进一步提高叶片式流动调整器的整流性能[8]。管束式流动调整器由布置在主管道内的19根以上的轴向平行管束构成[9],加工工艺简单,但流动阻力较大。格栅式流动调整器的典型代表是AMCA流动调整器[10],其原理与管束式流动调整器类似,但其分割密度大于管束式流动调整器,整流性能更佳,缺点是其流动损失也更大,而且装卸、检修较为烦琐[10]。孔板式流动调整器是在垂直于管道的板件上布置对称的多组不同开孔直径的整流装置[11],典型的有Laws调整器[12]、NEL调整器[13]、Zanker流动调整器[14]等。孔板式流动调整器具有加工工艺简单、整流性能强、压力损失大的特点。

翅片式流动调整器是1991年由美国Vortab公司的Smith等提出的一种内置翅片产生旋涡扰乱原始速度分布并利用二次流掺混形成均匀流场的整流装置[15-16]。根据其专利介绍,该结构能有效应用于气体、液体的整流中,可以以极低的压力损失为代价在较短的距离内实现均匀、无旋涡的速度分布[15]。目前,翅片式流动调整器按照结构主要分为直管式和弯管式两种,直管式调整器的翅片沿周向均匀布置,而弯管式则仅在弯管外侧沿流向布置,其基本原理和结构如图1所示。由图1可见,当流体流经管内翅片时,在翅片迎风面与背风面的压差作用下会产生强烈的剪切力[17],与航空领域的翼尖涡类似,这种剪切力会形成发夹涡并进一步演变为对转涡,大大促进边界层内外的质量与能量交换[18]。发卡涡结构是湍流边界层中的基础结构,由Theodorsen于1952年首次发现[19]。Gretta等则率先利用该原理将翅片作为涡生成器增强流体的掺混[20]。Elavarasan等利用平面激光诱导荧光(PLIF)技术观测了平板梯形翅片产生的发卡涡及其破裂后的对转涡结构[21]。Yang等采用粒子成像测速(PIV)技术进行了类似的研究,同样观测到了反向涡对[19]。Lin研究了翅片式涡生成器的高度、倾斜角等几何参数对其边界层分离控制的影响[22]。尽管关于翅片式涡生成器的研究比较广泛,但大多集中在高效换热领域[17],而且多与平板结构搭配,其应用于弯头内作为整流装置的相关研究鲜见公开报道。在核电站、舰船等场景内,水路管网十分复杂,泵或流量计上游短距离内极有可能布置有弯头结构,往往需要在弯头内进行整流工作。因此,研究翅片式弯管流动调整器具有十分重要的理论研究意义和工程应用价值。

图1 翅片式流动调整器整流原理示意图[15]Fig.1 Rectification mechanism of tab-type flow conditioner[15]

本文以翅片式弯头流动调整器为研究对象,采用3种梯度方向的速度分布作为进口边界条件,系统研究了该结构相对光滑弯管在不同雷诺数下的整流能力,包括压力均匀度、速度均匀度和流向角均匀度等,深入分析了其流场分布特征,揭示了其整流机理,总结了其压力损失特性。希望通过本文研究揭示翅片在弯管内的整流特性,为研制高效的弯管流动调整器提供参考。

1 数值方法

1.1 计算域设置

采用商用软件ANSYS CFX进行定常数值模拟,带翅片计算域布置参照文献[15],主要结构包括抗涡肋、二次抗涡肋、上游翅片、下游翅片等,如图2所示。其中上游翅片与抗涡肋为一体式结构,下游翅片则为离散的翅片组。计算域主要尺寸见表1,圆管内径D为154.08 mm,上游进口段长度Lu=1D,下游发展段长度Ld=10D。对照计算域为相同尺寸的光滑管。上下游翅片长度L均为0.5D,宽度W均为0.4D,收缩角α均为15°,抬升角β分别为50°、40°,其他几何参数详见文献[15]。

(a)三维图

表1 计算域主要几何参数

1.2 边界条件

基于CAP1400核电机组的管路流动参数,表2列出了本文研究的边界条件。模拟工质为25 ℃水,进口速度与6×105～1.2×106的雷诺数相匹配,出口压力为0.18 MPa。进口设置了3种均匀线性速度梯度,用于模拟最恶劣的弯管进口不均匀速度分布,如图3所示。图中,变量VR是无量纲速度,定义为当地速度与进口平均速度之比。相关算例按照梯度方向简写为PY、PZ、NZ,同时,光滑管结构和流动调整器结构分别简写为SP和FC,如SP-PY代表进口为+Y方向速度梯度的光滑管算例,而FC-NZ代表进口为-Z方向速度梯度的流动调整器算例。值得说明的是,由于+Y与-Y方向的进口线性速度分布在下游造成的流动状态是沿XZ平面对称的,为了避免冗余,本文没有开展-Y方向速度梯度的相关研究。

表2 边界条件参数Table 2 Parameters of boundary conditions

(a)SP-PY

1.3 湍流模型验证

现有文献中关于翅片式流动调整器的实验研究数据较少,本文以水为工质,对双扭管(两个连续弯管)下游布置Zanker式流动调整器的实验[23]进行湍流模型验证,其流体域如图4所示。采用定常数值模拟常用的k-ε、RNGk-ε、k-ω和SSTk-ω模型进行湍流模型验证,验证结果如图5a所示。对比工况的雷诺数为6.0×105,对比数据为无量纲轴向速度,其中Vb为充分发展段的流动速度,r为流动调整器下游3D截面处相对管道轴心的高度,以管道轴心为界,下侧为负,上侧为正。可以看出,相对于实验结果,数值模拟得到的速度分布曲线要更平滑一些;4种湍流模型的计算结果中,SSTk-ω模型的结果与实验结果最接近,最大偏差为13.27%,平均偏差2.71%。由于壁面附近速度梯度较高,呈现较强的各项异性特征,因此采用各向同性涡黏性假设的雷诺时均方法求解边界层时会存在一定的误差。SSTk-ω湍流模型得到的误差在可以接受的范围内,因此,本文采用SSTk-ω模型进行数值仿真研究。

图4 湍流模型验证计算域Fig.4 Computational domain for turbulence model validation

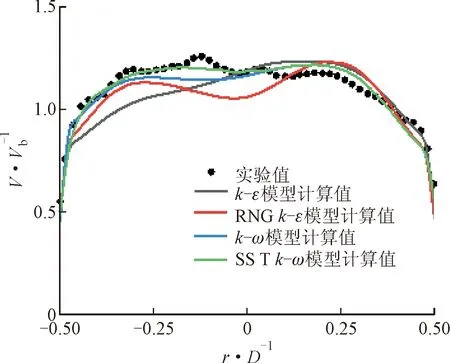
(a)速度分布预测结果与实验数据对比(Re=6.0×105)

为了检验所选湍流模型对压力损失的预测精度,对比了不同雷诺数下数值模拟所得压力损失系数与实验结果[23]的差异见图5b。定义压力损失系数

(1)

式中:ΔP为流动调整器前后压力差;ρ为流体密度。由图5b可以看出,数值模拟的压力损失系数略高于实验结果,最大偏差3.72%,平均偏差1.88%,相对误差较小,说明所用数值方法可以较准确地预测流动调整器的压力损失系数。

1.4 网格无关性验证

由于翅片式流动调整器包含多个方向的翅片,结构较为复杂,因此对计算域采用非结构化网格剖分。近壁面第一层网格厚度0.002 mm,增长率为1.2,边界层层数为30。经计算,壁面Y+为1.0以下,符合所采用的SST湍流模型要求。壁面网格和横截面网格如图6所示。本节采用5组精细度的网格进行网格无关性验证,按照壁面和主流等比例加密的原则进行加密,网格数量分别设置为200万、300万、400万、500万、600万。验证结构为FC-PY,进口雷诺数为9×106,对比数据为弯管下游5个位置处的速度均匀度,验证结果如图7所示。

(a)壁面网格

从图7可以看到,在网格数量超过400万后,弯头下游5个截面数据点的速度均匀度相对误差很小,500万与600万网格所得到的预测结果的最大相对误差为0.4%。为了平衡计算精度要求与计算资源消耗,本文所有算例均采用500万网格对应的加密设置,即最大体网格限定10 mm,翅片表面加密至1.5 mm。

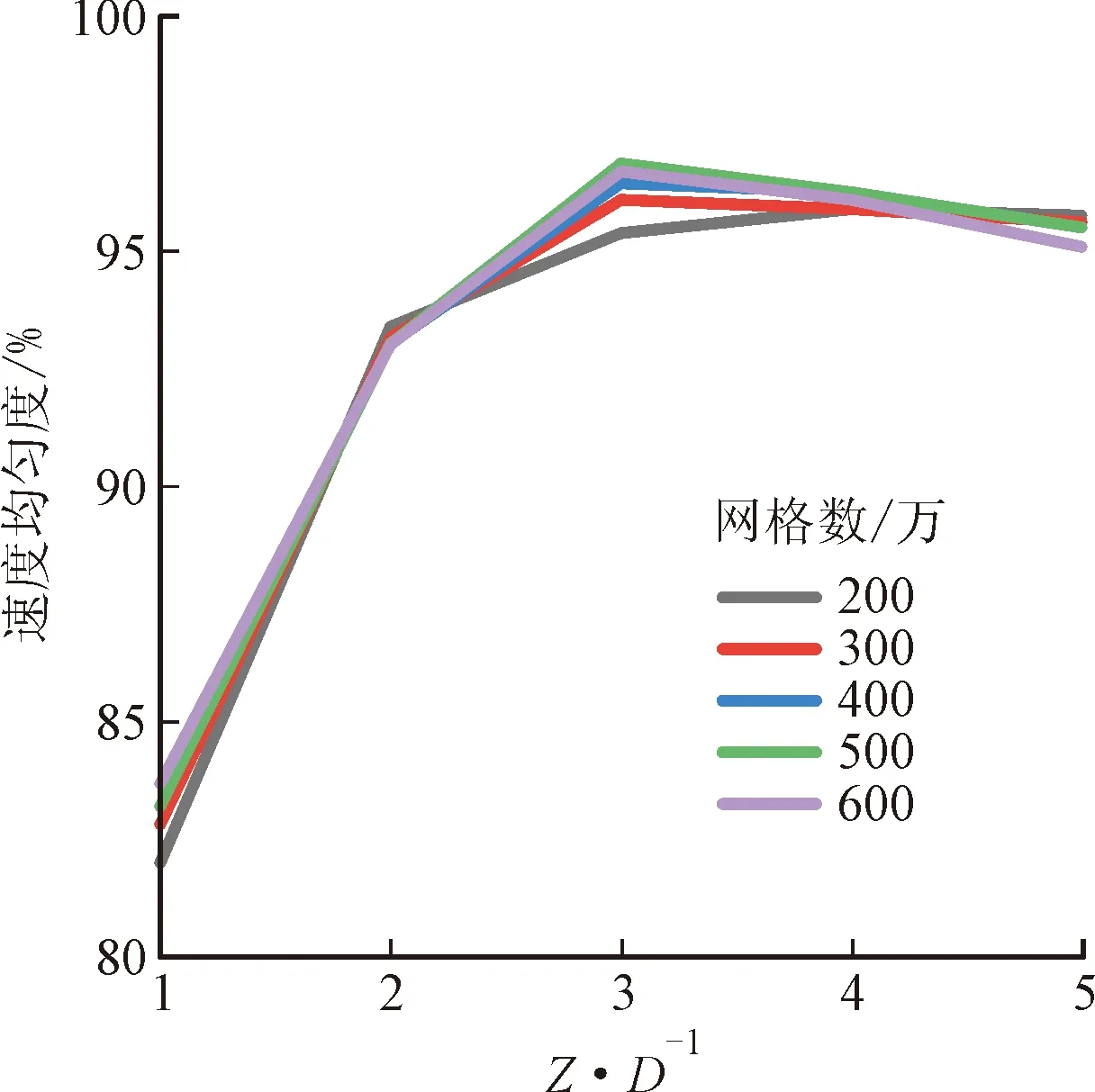
图7 网格数量对弯管下游速度均匀度的影响Fig.7 Effect of grid number on velocity uniformity

2 流场均匀度评价方法

流场均匀度评价采用3个参数,即压力均匀度、速度均匀度和流向角均匀度。数据采集方法为弯头下游1D～5D以1D距离为间隔设置截面,在截面上以点阵的方式收集当地压力、速度和流向角。数据点分布示意如图8所示,共8条辐线,每条辐线上有10个数据点,加上原点共81个采样点。

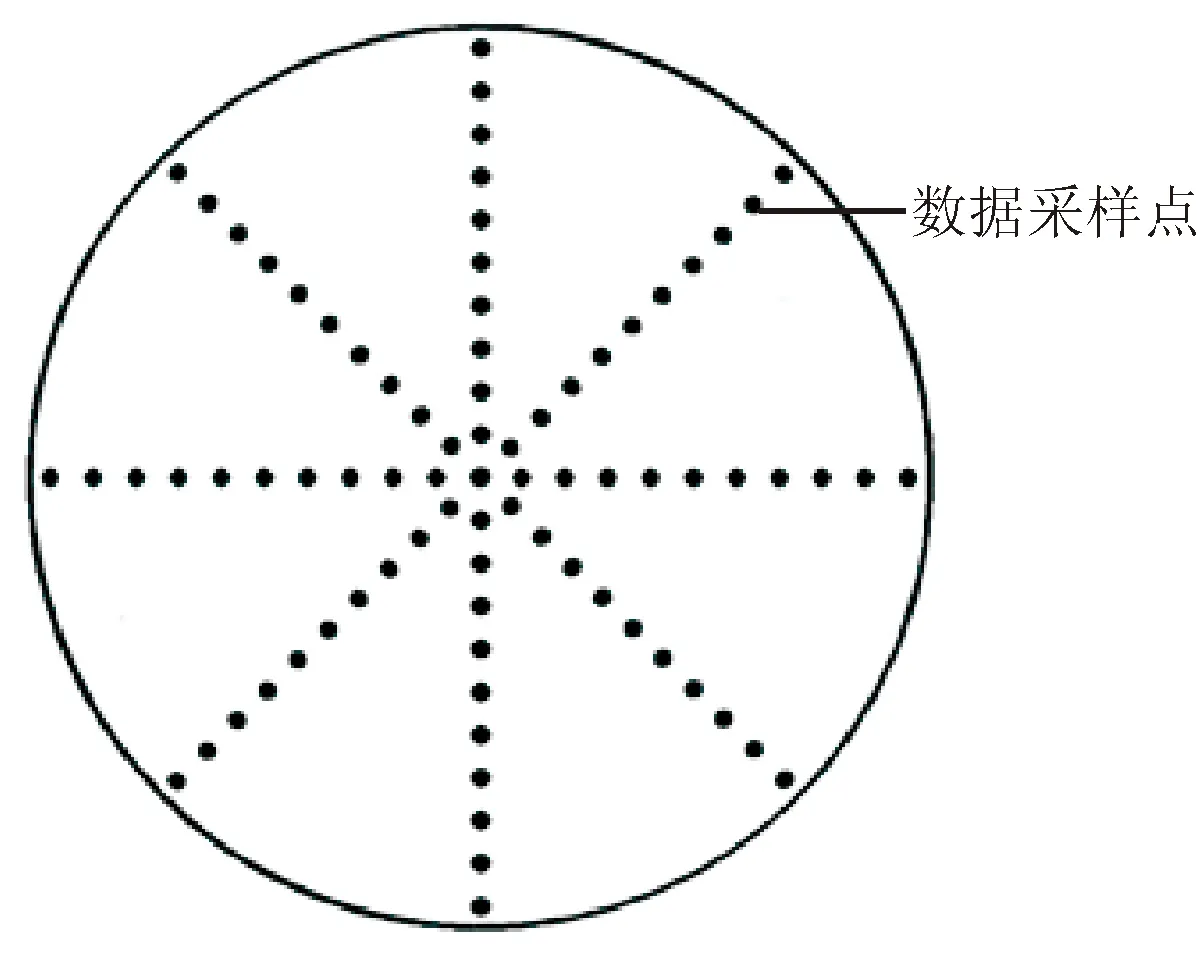
图8 截面数据点分布示意图Fig.8 Distribution of data sampling points

压力均匀度和速度均匀度的计算公式[24]为

(2)

(3)

其中Vj为第j个采样点的压力或速度,n为采样点个数。通过比较不同工况下的C值来评判截面上流场的均匀度,C值越大,流场均匀度越高。

根据GB-T 17611—1998,旋涡角θ为横截面某给定点的局部速度与管道轴线之间的夹角。考虑到无量纲处理要求分母不为0,定义旋涡角的余角为流向角θ,其计算方法为

(4)

式中:Vw代表给定点速度在管道轴线方向上的分量;V代表给定点的速度。

流向角均匀度的定义为

(5)

式中:θj为第j个采样点的流向角。Cθ越大,流场均匀度越高。

3 结果与分析

本文算例共两种几何结构,即光滑管与翅片式弯头流动调整器,进口速度共5种,用于匹配5种雷诺数(6×105、7.5×105、9×105、1.05×106和1.2×106),进口速度梯度方向共3种。计算结果显示雷诺数对于两种结构各自的流场特性、均匀度等没有明显影响,为避免结果繁杂,除了3.3节关于压力损失分析外,其他部分仅展示进口雷诺数为9×105的结果。

3.1 不同进口速度分布下的整流性能对比

压力均匀度影响管路的稳定情况,速度均匀度体现了流体的流量分布情况,流向角均匀度体现了流体流动的旋涡尺度大小。通过这3个参数可以系统地验证流动调整器在不同边界条件下的整流性能及适用范围。

图9是流动调整器对弯头下游压力均匀度的影响。可以看到,光滑管弯头下游的压力均匀度非常高,3种进口边界条件中,只有PY方向的速度分布产生了略低的压力均匀度,且在5D范围内呈现持续下降的趋势。相比之下,增加流动调整器后,压力均匀度均在研究范围内呈上升趋势,数值上与光滑管弯头产生的压力均匀度在同一区间,均保持在98%以上。可以说,在压力均匀度方面,增加翅片式弯头流动调整器没有显著的影响,但其产生的均匀度完全符合测量要求。

图9 流动调整器对压力均匀度的影响(Re=9×105) Fig.9 Effect of flow conditioner on pressure uniformity(Re=9×105)

图10是流动调整器对速度均匀度的影响。可以看到,在3种边界条件下,流动调整器均能在弯头下游3D范围内将速度均匀度提升至85%以上,在5D范围内提升至90%以上。在下游3D处,流动调整器产生的速度均匀度相对于光滑弯头在PY、PZ、NZ条件下分别提升了31%、21%、36%。其中,PY、PZ条件下的光滑弯头下游速度均匀度提升较快,而NZ条件下的速度均匀度始终在65%以下,这体现了弯头整流相对于直管整流的特殊性,即进口速度梯度方向的改变会对下游流动产生很大的影响。同时,也体现了翅片式流动调整器对于弯头进口不均匀来流的整流能力是显著而全面的。

图10 流动调整器对速度均匀度的影响(Re=9×105) Fig.10 Effect of flow conditioner on velocity uniformity(Re=9×105)

图11为流动调整器对流向角均匀度的影响。可以看出,在PZ和NZ条件下,光滑弯头下游流向角均匀度全程高于90%,而同样条件下的翅片式流动调整器反而降低了弯头下游的均匀度。在PY条件下,两种结构在弯头下游产生的流向角均匀度均在80%附近,流动调整器略微提升了均匀度。这说明,在多数情况下,翅片式流动调整器对于削弱弯头下游的旋涡强度没有明显的作用,若要在短距离内实现无旋涡流动则需在下游直管段搭配管束式整流器等其他装置。

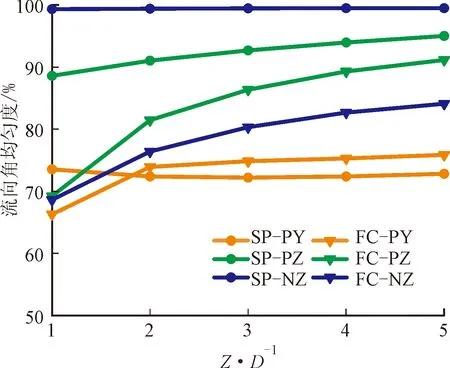
图11 流动调整器对流向角均匀度的影响(Re=9×105)Fig.11 Effect of flow conditioner on flow angle uniformity(Re=9×105)

3.2 流场特性分析

图12、图13分别展示的是PZ条件下两种弯管内Q准则等值面和下游涡量分布,其中ωz为涡量。Q是流体仿真中用于捕捉涡核位置的常用参数,其定义为

(6)

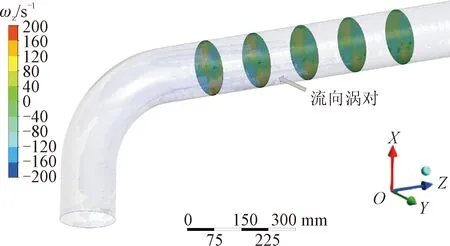
图12 光滑弯管内的Q准则等值面和下游涡量分布(SP-PZ,Re=9×105)Fig.12 Q-criterion iso-surface and vorticity distribution in smooth pipe(SP-PZ,Re=9×105)

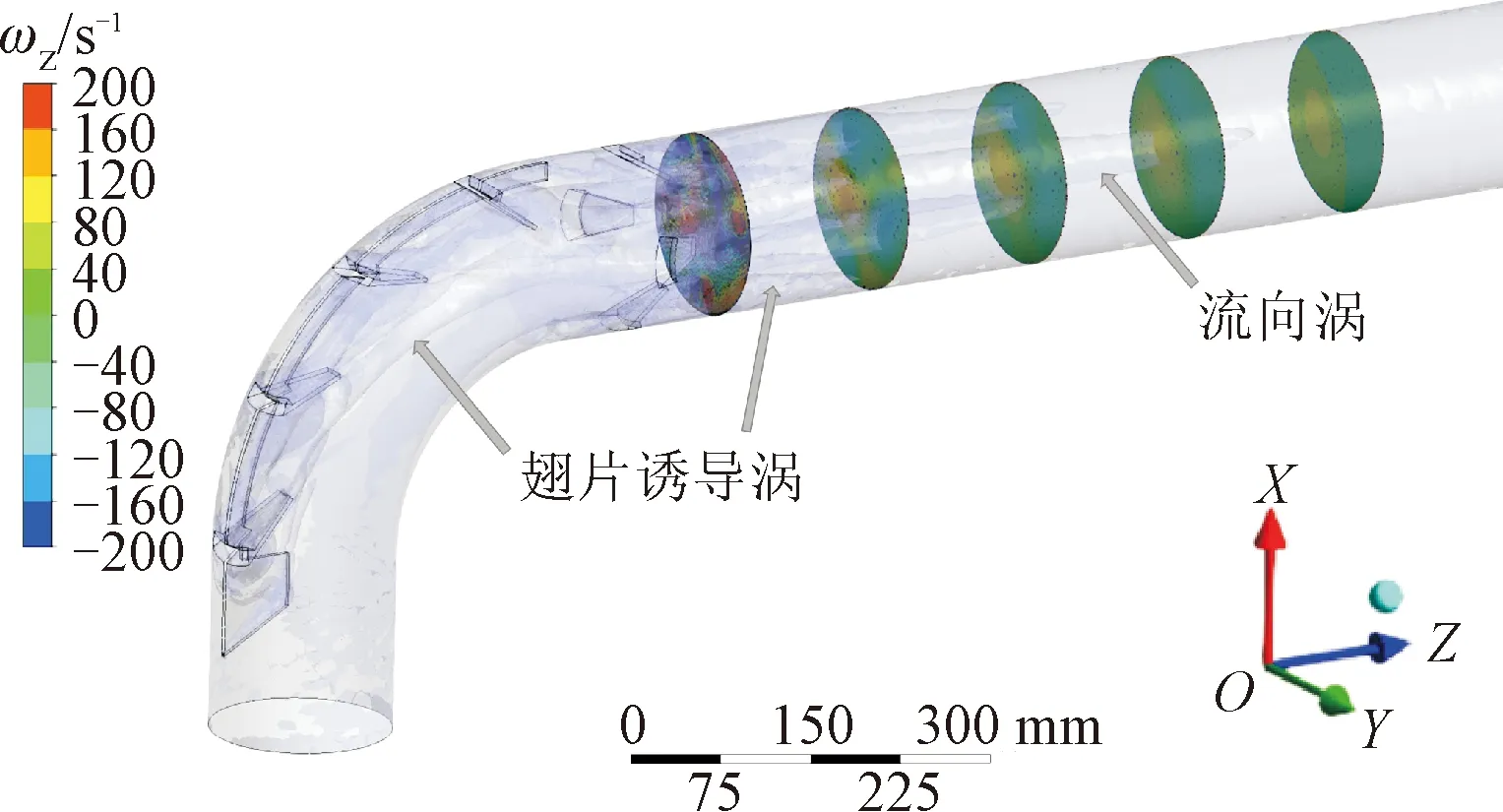
图13 翅片式流动调整器内的Q准则等值面和下游涡量分布(FC-PZ,Re=9×105)Fig.13 Q-criterion iso-surface and vorticity distribution in tab-type flow conditioner(FC-PZ,Re=9×105)

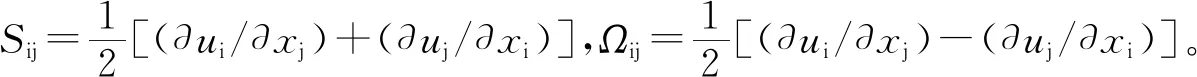
在均匀来流下,弯管下游一般会出现对转形态的“迪恩涡”。然而,在PZ条件下,弯头内侧速度高,在弯头下游诱发了两组流向涡对,体现了不均匀来流对流动结构的影响。增设翅片后,其上游翅片前后面间的压力差会在翅片边缘诱导产生指向弯头内侧的对转涡对,在弯头下游1D距离内与其下游翅片诱发的对转涡对相互掺混融合,产生新的流向涡。在这一过程中,原始线性速度分布被扰乱,在弯头下游1D后逐渐形成新的速度分布。

图14为光滑管内3种进口条件下的流线分布。在PY条件下,高速流体和低速流体在进入弯头后在压力梯度的驱使下形成大尺度的流向涡,并在弯头下游始终保持该形态,可以看到,管壁边界层的剪切和流体之间的动量交换在一定程度上削弱了这种速度差,但仍然需要较长的直管段才能完全消除。在PZ条件下,弯头内侧的高速流体和弯头外侧的低速流体同样会在压力梯度的作用下产生动量交换,并由此形成复杂的小尺度流向涡,其速度不均匀程度在这一过程中得到削弱。在NZ条件下,原始速度差产生的压力梯度可以在一定程度上抵消流经弯头时产生的径向压力梯度,因此在经过弯头后,原始速度分布得以保留,没有产生宏观尺度的流向涡。

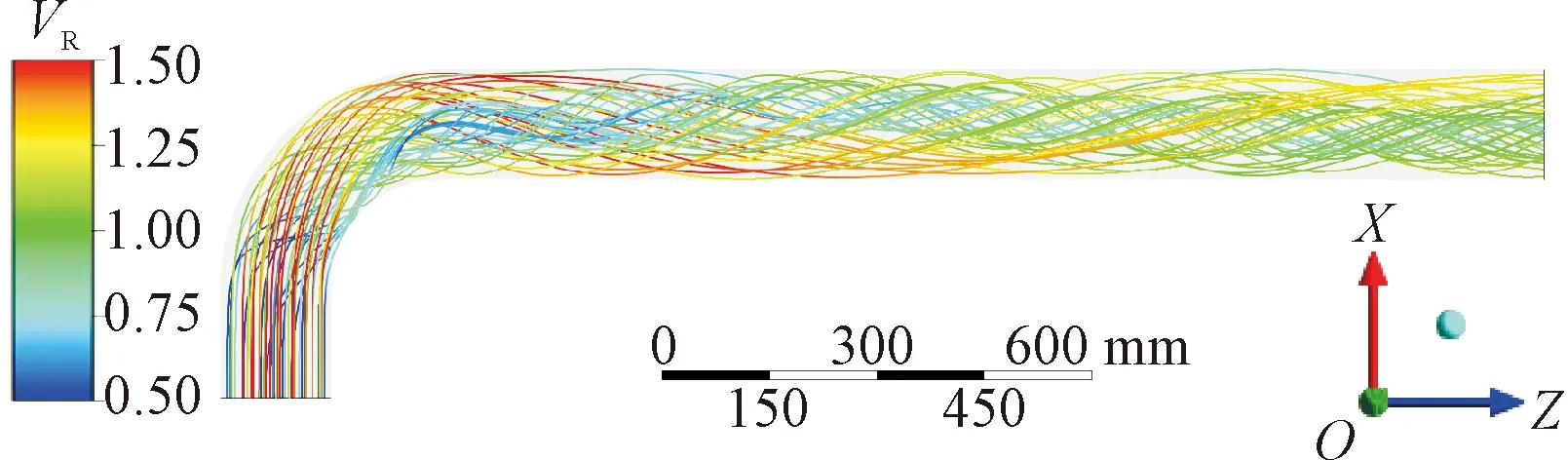
(a)SP-PY

图15是不同进口条件下翅片式流动调整器内的流线分布(Re=9×105)。在PY条件下,弯头内的单螺旋流向涡被翅片诱导涡搅拌干扰,在弯头下游1D位置前充分掺混,有效降低了速度差,但其“以涡扰涡”的原理使其无法削弱流向涡的强度。在PZ条件下,弯头外侧的低速流体在流经上游翅片时产生了指向弯头内侧的诱导涡对,但由于其动量和强度较低,无法进行高低速流体间的充分掺混,需要下游翅片诱导涡的补充才能完成动量交换,同时会附带产生低强度的流向涡。在NZ条件下,弯头外侧的高速流体在流经上游翅片时产生了高强度的诱导涡对,冲击到弯头内侧壁面,与该位置处的低速流体进行充分动量交换。在经过弯头后,依然有部分流体的动量难以被翅片有效削弱。

(a)FC-PY

图16和图17分别给出了弯头下游不同位置截面上Z方向涡量分量和无量纲速度的分布情况。涡量分布方面,对于光滑管来说,在PY条件下,弯头下游存在明显的Z方向单螺旋流向涡,在研究范围内没有削弱。在PZ条件下,弯头内外侧流体的充分掺混形成了有对称特征的两组对转涡,且维持了较远距离。在NZ条件下,原始速度分布在经过弯头后得以保留,没有剧烈的动量交换过程,因此没有产生大尺度流向涡。对翅片式流动调整器来说,在1D位置处可以看到下游翅片形成的多组诱导对转涡,然而其位置和形态受到主流速度分布的影响。在PY条件下,单螺旋流向涡的周向动量使下游翅片诱导涡对沿顺时针方向偏离了翅片位置,经过动量交换后,下游仍存在单螺旋涡。在PZ条件下,经过整流后弯头下游仅存在一组流向对转涡。在NZ条件下,上游翅片诱导涡对弯头内侧的强烈冲击使得下游翅片诱导涡对向弯头外侧方向偏离。经过掺混后,下游仍存在一对大尺度“迪恩涡”。

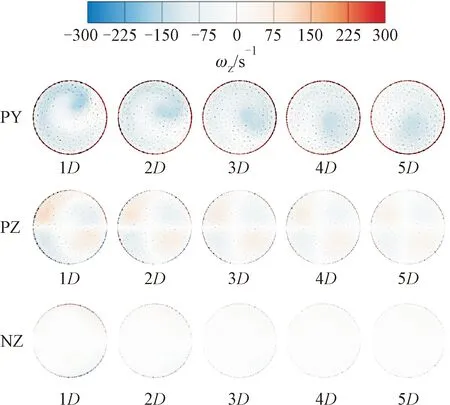
(a)光滑管

(a)光滑管

无量纲速度VR分布方面,对光滑管来说,在PY条件下,高速流体冲向管壁并沿壁面呈周向运动,以单螺旋涡包裹内部的低速涡核。在PZ条件下,弯头内侧高速流体沿壁面以对转涡的形态从两侧包裹内部低速流体,并进一步演变为两组对转涡。在NZ条件下,由于没有形成流向涡,高低速流体在弯头下游保持进口速度分布,缺乏剧烈的动量交换过程。对于弯头来说,来流速度梯度方向的影响会与弯头方向的影响产生耦合叠加,因而不均匀来流产生的不均匀度情况要比在直管更复杂多变,更难以消除。对翅片式流动调整器来说,在PY条件下,单螺旋流向涡产生的速度差在下游翅片诱导涡的有效掺混下大幅降低,弯头下游3D距离后的速度分布比较均匀。在PZ条件下,管壁附近的流体在经过整流后相对于管道中心的流体有一定的速度差,且在弯头下游3D～5D距离呈现快速降低趋势。在NZ条件下,弯头外侧的高速流体在流经上下游翅片后依然具有相当的动量,并在下游弯头外侧翅片诱导涡的裹挟下在管道中心形成横向高速带。尽管不能在5D距离内完全消除速度差,但经过整流后的速度差在各个进口条件下、各个下游位置处均明显优于光滑管。

3.3 不同进口雷诺数下的压力损失对比

流动调整器在改变流体速度分布的同时会难以避免地造成流动损失,图18为在所研究的雷诺数范围内,翅片式弯头流动调整器产生的压力损失。根据文献[25],不均匀来流的影响需要200D直管才能彻底消除。因此,图中还对比了充分发展流动在200D直管内产生的压力损失,其计算公式为

(7)

式中:l0为管内流动距离;f为摩擦系数,参照下式确定。

(8)

从图18可以看出,随着进口雷诺数的增加,各种工况的压力损失都有所提高,其中,PZ条件下的翅片式流动调整器产生的压力损失最低,其他两种进口速度分布产生的压力损失情况几乎完全相同。一方面,由于翅片在管道内的投影面积较大,其引起的压差损失要比诱导涡引起的掺混损失大很多。在PY和NZ条件下,高速流体会在弯头内冲击翅片,造成翅片正面较大的滞止压力,而在PZ条件下,冲击翅片的是低速流体,在翅片正面产生的滞止压力较低,其引起的诱导涡进一步阻止了高速流体向弯头外侧翅片流动,所以PZ条件下的压力损失明显低于其他两种条件。另一方面,尽管PY条件产生的压差阻力低于NZ条件,但其二次流结构更复杂更不均匀,因而其掺混损失要高于NZ条件,总压力损失与NZ条件接近。在研究范围内的各种工况下,翅片式弯管流动调整器产生的流动损失都远低于充分发展的流动在200D的直管内所造成的压力损失。

图18 弯头流动调整器与普通直管压损比较Fig.18 Comparison of pressure losses between elbow flow conditioner and straight pipe

表3横向对比了翅片式弯头流动调整器与前文提到的其他类型典型流动调整器的压力损失系数。需要说明的是,流动调整器的压力损失系数随雷诺数变化略有变化,但一般而言幅度不大,因此表中翅片式流动调整器的压力损失系数为各个雷诺数下的压损系数平均值。其他流动调整器的压力损失系数来自文献[5]和文献[23]。从表3可以看出,翅片式弯头流动调整器的压力损失系数随进口条件的变化有较大幅度的变化,为0.36～1.17,但基本与管束式流动调整器相当,高于简单的八叶片式流动调整器,低于大流阻的孔板式流动调整器。

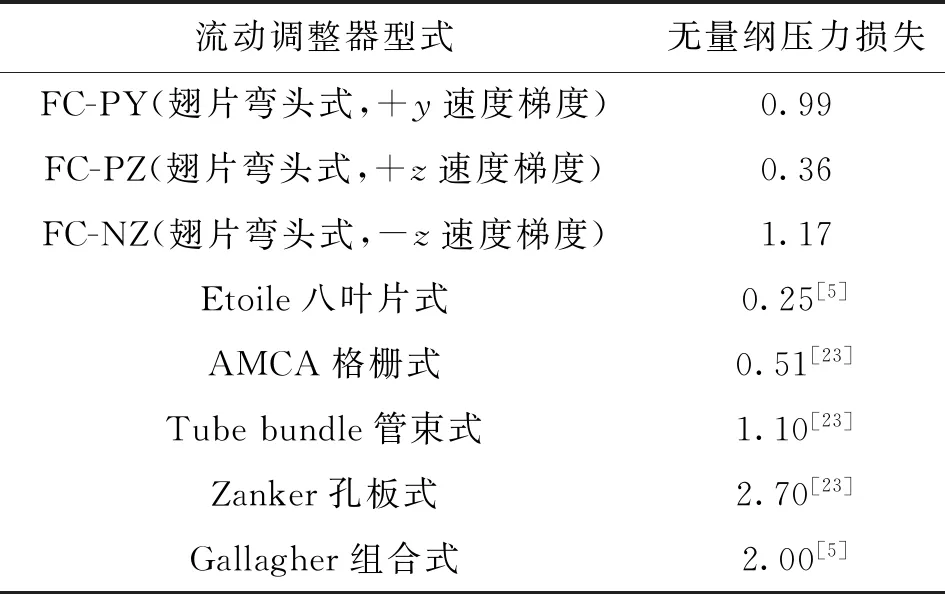
表3 各种流动调整器无量纲压力损失比较Table 3 Comparison of pressure losses among different flow conditioners

4 结 论

(1)翅片式弯头流动调整器的主要作用机理在于利用翅片前后的压差在翅片边缘产生对转的诱导涡,使部分弯头外侧的流体冲击弯头内侧,增强动量交换,扰乱来流速度分布,并利用下游翅片诱导涡加强掺混,降低流体间的速度差。

(2)翅片式弯头流动调整器对弯头下游压力均匀度影响不大,对速度均匀度有21%～36%的提高,对流向角均匀度的影响随进口速度梯度方向的变化而变化,一般呈负面效果。

(3)在泵或流量计前存在弯头的情况下,来流速度梯度方向的影响会与弯头压力梯度的影响产生耦合叠加,因而来流产生的不均匀度情况要比在直管内更复杂多变,更难以消除。

(4)翅片式弯头流动调整器适用于削弱不均匀来流对弯头下游流动结构的影响,能够在下游短距离内构建均匀的速度分布,但难以消除直管段内的流向涡。

(5)翅片式弯头流动调整器的压力损失系数随进口条件的变化在0.36～1.17间变化,基本与管束式流动调整器相当,高于简单的八叶片式流动调整器,低于大流阻的孔板式流动调整器。