超声速二元机翼随机混沌运动分析*

闫 盖,方明霞,杨英豪,沈海军

(1. 上海第二工业大学 工学部， 上海 201209； 2. 同济大学 航空航天与力学学院， 上海 200092；3. 上海飞机设计研究院， 上海 201210)

气动弹性是飞行器设计中备受关注的重要问题，主要气动弹性现象有颤振、抖振、动力响应等[1-2]。其中，动力响应是指弹性系统受到与自身系统无关的、随时间任意变化的外界干扰力作用而发生的强迫振动，外界扰动可以是谐和的、周期的、脉冲的或随机的[3]。在航空动力学领域中,随机扰动普遍存在，它主要是由飞行器飞行过程中空气热力、风力和尾涡等随机因素相互作用形成的大气湍流引起的。从强度观点来看，飞机结构可能在严重的湍流中由于超载而遭破坏，中等大小的湍流则是飞机结构疲劳损伤的主要来源[4]。因此，结合气流扰动的机翼系统动力学特性研究能更好地反映实际工况。近年来，考虑外界扰动的机翼气动弹性问题正受到越来越多学者的关注。

Poirel和Price[5-8]研究了二元机翼在湍流随机扰动作用下的颤振问题，考虑了机翼结构线性和立方非线性情况，将湍流近似为高斯随机过程，从概率密度和最大Lyapunov指数分析了二元机翼的随机动力学行为，指出了随机激励下的颤振点较确定性系统颤振点提前，且与激励的强度密切相关。文献[9]采用能量随机平均法，求解FPK(Fokker-planck-kolmogorov)方程，获得随机激励下的一元机翼分岔点，并分析了系统的随机Hopf分岔特性。文献[10]利用摄动法获得了二元机翼在非高斯色噪声作用下的Lyapunov指数，分析了二元机翼在随机激励下的稳定性。文献[11]采用随机平均法得到二元机翼在宽带噪声激励下的Lyapunov指数，探讨了随机噪声谱密度对机翼稳定性的影响。文献[12]采用随机减量法和矩阵束法识别紊流激励中的模态参数，提出了一种紊流激励下的颤振边界预测方法。可以看出，对随机激励下的机翼动力学特性研究主要集中在随机颤振预测、随机分岔特性研究中。

而对飞行器混沌运动问题的研究，目前主要针对考虑飞行器结构非线性的自治系统。如文献[13]采用伽辽金法对考虑几何非线性的长直机翼运动方程进行离散，通过数值方法分析了机翼的颤振及混沌运动特性。文献[14]研究分析飞行器操纵面的操纵刚度对混沌运动特性影响较小，而阻尼对系统的混沌特性影响较大。文献[15]采用数值模拟方法和预测程序，研究了不可压缩流中具有结构二次、三次非线性项的二元机翼系统分岔和混沌特性。可以看出，目前的研究多是从机翼非线性结构参数出发，研究系统的颤振、抖振问题，旨在提高系统的临界飞行速度、优化系统的结构参数、改善控制方法等。但从外在随机激励角度探讨二元机翼系统的复杂动力学特性较少，且采用解析方法对超声速二元机翼的随机混沌特性进行研究更为少见。为此，本文将从定性和定量角度出发，根据Kapitaniak对随机混沌的定义(即随机混沌过程必须满足两个条件：①概率密度函数具有多个最大值；②概率时差图具有康托集合结构)，提出一种半解析方法探讨随机激励下二元机翼的混沌运动特性。即通过联合使用累积量截断法、非高斯截断法获得系统的二维联合概率密度函数及系统的概率时差图，采用Kapitaniak方法分析系统在不同扰动强度下的随机混沌特性，并通过数值方法对分析结果进行验证。本文研究不仅可以分析随机激励下扰动强度、飞行器结构参数对系统混沌域的影响，还可以推广到其他随机非线性的大型复杂系统的动力学研究中，推动高维非线性系统动力学行为基础研究的发展。因此本文研究具有重要的理论和实际意义。

1 二元机翼随机非线性动力学方程

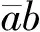
图1 二元机翼模型Fig.1 Model of a two-dimensional airfoil

采用第二类拉氏方程获得受随机扰动的二元机翼动力学方程为：

(1)

文献[16-17]研究表明，在飞行马赫数为2～5时，活塞理论比较适合机翼气动力计算。为此本文采用三阶活塞理论给出了机翼非线性气动力和气动力矩：

(2)

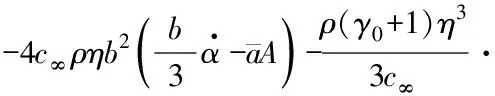
(3)

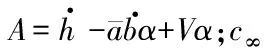
(4)

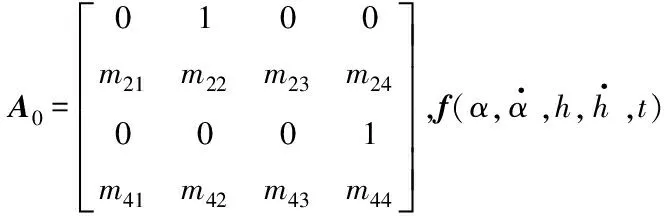
A0矩阵中各元素表达式如下：

4χαc∞ρηb2-χαbch)

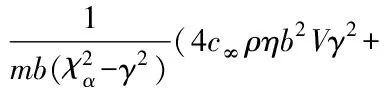
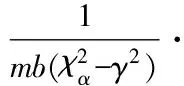
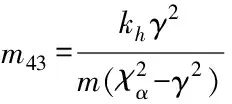
其中

S1=-Fh+σhξh(t)

S2=-kα2α3-Fα+σαξα(t)

2 采用中心流形方法对系统进行降维

由于方程(4)为4维非线性动力学方程，直接对其动力学特性进行研究比较困难，为此首先采用中心流形方法对系统进行降维。由于中心流形定理仅适用于自治系统，因此首先要对随机激励进行变换，本文采用Monte Carlo法将功率谱密度函数变换成多项余弦函数叠加的形式，并通过扩大向量将非自治系统转换为自治系统。

通过Routh-Hurwitz判据得到：Ma<3.985时，系统稳定，响应收敛到平衡点；3.9854.086时，系统发散，因此，Ma*=3.985为系统Hopf分岔点。

取μ=Ma-Ma*(Ma*=3.985)为分岔参数，给定系统参数，引入非奇异变换x=py，其中y=(y1,y2,y3,y4)T，p为相对应于系统中零平衡点的Jacobi矩阵的第1项实部、第2项实部和虚部以及第4项实部构成的方阵，代入方程后系统化成

(5)

根据中心流形定理，得到中心流形函数

(6)

o(3)表示三阶以上的高阶小量，忽略此量，可得到约化方程(7)，其中Δ1、Δ2是经过变换的随机激励。

(7)

3 二维联合概率密度函数求解

根据Kapitaniak对随机混沌特性的定义：二维联合概率密度分布具有多峰且概率时差图具有典型的康托集合结构时，系统具有随机混沌特性。为此首先对系统的二维联合概率密度函数进行分析。由于方程(7)为非线性方程，故本文联合利用累积量截断法、非高斯截断法对系统的二维联合概率密度函数进行求解。方程(7)的伊藤随机微分方程形式如下：

(8)

式中，D1、D1为随机激励强度。

由式(8)得到相应的FPK方程，求得矩方程表达式为：

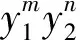
(10)

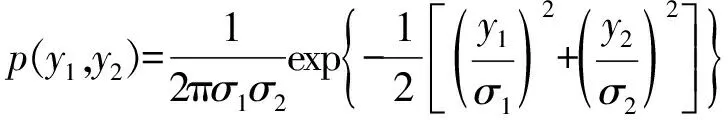
(11)

4 二元机翼随机混沌特性分析

现通过二维联合概率密度函数曲线、概率时差图对二元机翼的随机动力学特性进行研究。由于机翼俯仰自由度的振动幅值比沉浮自由度的振动幅值大，故本文主要研究俯仰角-俯仰角速度的概率密度曲线。现将系统发生颤振时的来流马赫数Ma=3.985作为分界线，以此将系统划分为颤振前区、颤振后区，并研究来流马赫数分别为Ma=3、Ma=5时系统颤振前区和颤振后区的动力学特性。

根据第3节求解二维概率密度函数的方法，获得系统颤振前区和颤振后区在随机扰动作用下的概率密度函数。随机扰动强度根据文献[17]添加，即弱随机扰动取值0.01，一般随机扰动取值0.1，强随机扰动取值0.5。图2是在颤振前区Ma=3时，在随机扰动强度分别为0.01、0.1和

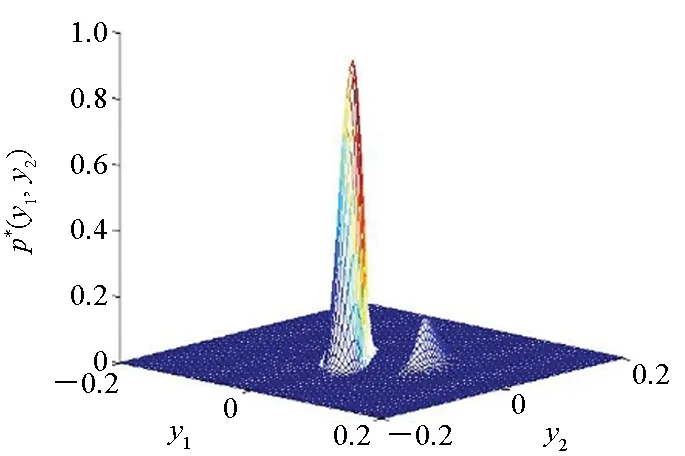
(a) D=0.01

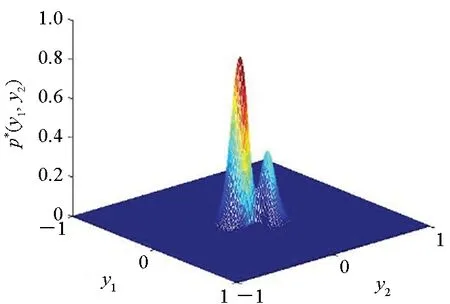
(b) D=0.1

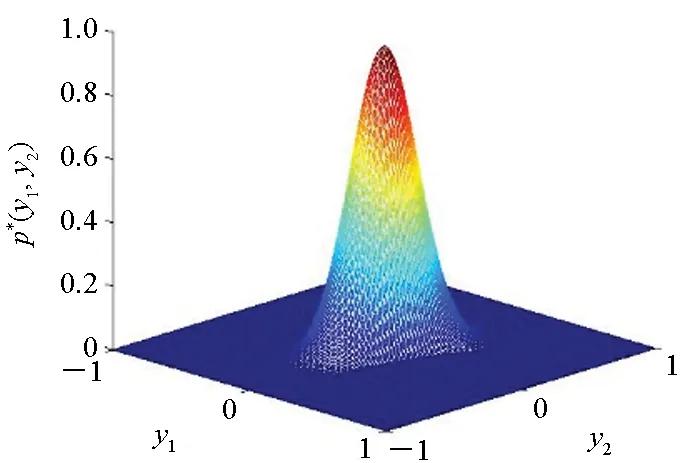
(c) D=0.5图2 不同随机扰动强度下的二维概率密度图(Ma=3)Fig.2 Two-dimensional probability density diagram with various disturbance intensities(Ma=3)

0.5时系统的二维概率密度分布图；图3是在颤振后区Ma=5时不同随机扰动强度下的二维概率密度分布图。

(a) D=0.01

(b) D=0.1

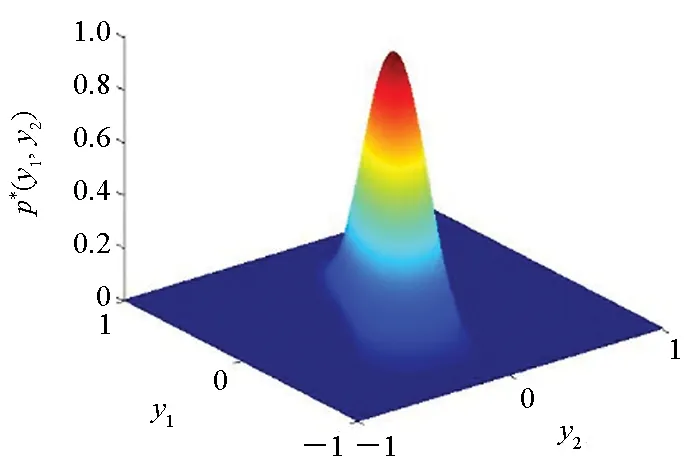
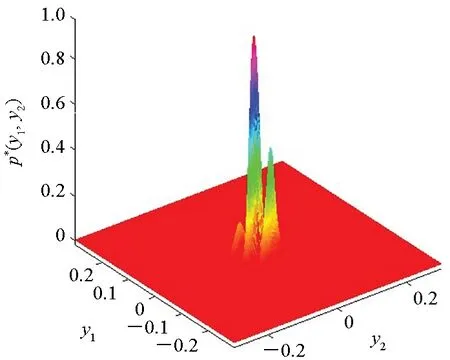
(c) D=0.5图3 不同随机扰动强度下的二维概率密度图(Ma=5)Fig.3 Two-dimensional probability density diagram with various disturbance intensities(Ma=5)

从图2、图3可以看出：二维概率密度在颤振前区时，形状在弱随机扰动下为分离双峰，一般随机扰动下为相邻双峰，强随机扰动下变为单峰；在颤振后区时，形状在弱随机扰动下为多峰，一般随机扰动下变为双峰，强随机扰动下变为单峰。并且在颤振前区和颤振后区的二维联合概率密度形状在弱随机扰动下不同，而在强随机扰动下形状相似，由此可知系统拓扑结构发生了质变，系统发生了P分岔。

根据概率密度的多峰状态，为了判断系统在弱随机扰动、一般随机扰动下是否进入了混沌运动状态，现绘制概率时差图对系统的动力学特性进行进一步分析，因为二元机翼在一定来流马赫数下，受一定强度的随机激励影响发生分岔、进入混沌运动状态时间非常短，因此绘制概率时差图的时延也较小，本文选取0.01 s。图4为颤振前区，在弱随机扰动、一般随机扰动下的概率时差图；图5为颤振后区， 在弱随机扰动、一般随机扰动下的概率时差图。

从图4、图5可以发现，在颤振前区和颤振后区，系统受弱随机扰动强度和一般随机扰动强度下，概率时差图均出现了典型的康托集合效应，即在某一位置附近出现频率明显高于其他位置。结合其二维概率密度呈现多峰形状，因此系统发生了Kapitaniak定义下的随机混沌。

(a) D=0.01

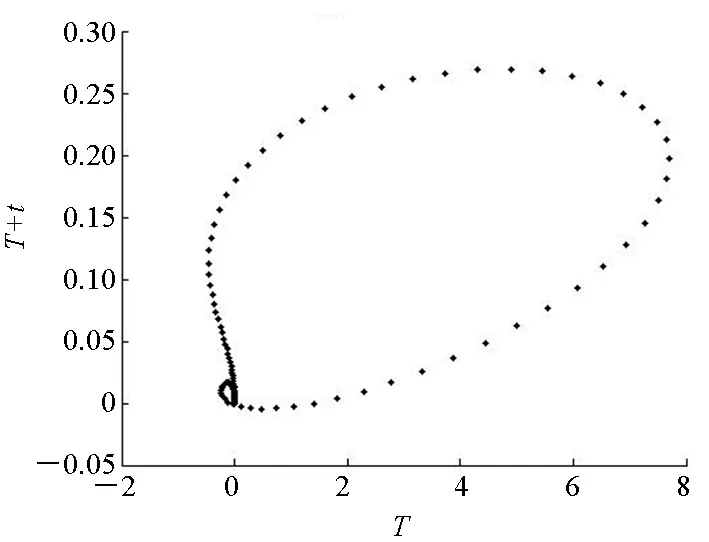
(b) D=0.1图4 不同扰动强度下颤振前区的概率时差图(Ma=3)Fig.4 Probability time difference diagrams with various disturbance intensities(Ma=3)

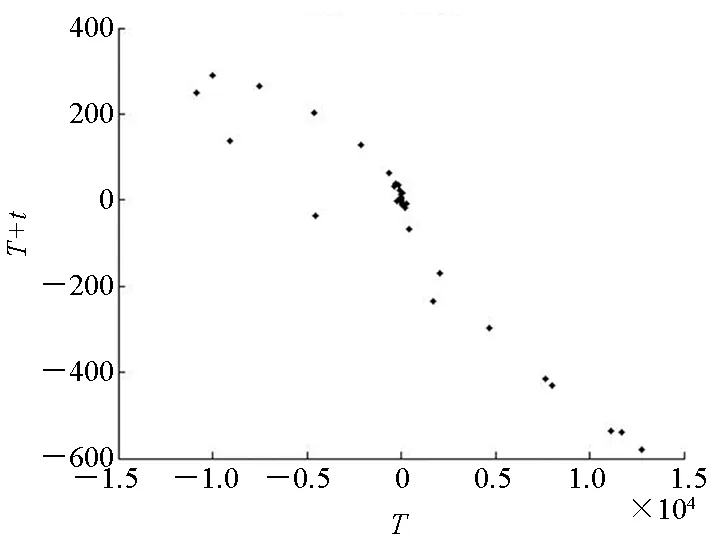
(a) D=0.01

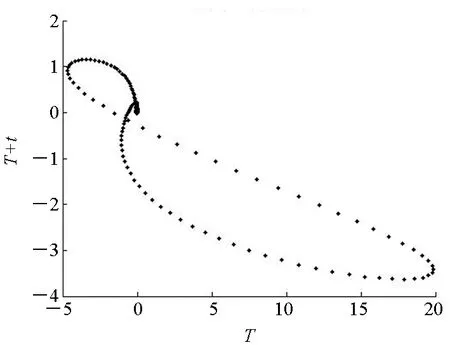
(b) D=0.1 图5 不同扰动强度下颤振后区的概率时差图(Ma=5)Fig.5 Probability time difference diagrams with various disturbance intensities(Ma=5)

由于强随机扰动下二维联合概率密度函数为单峰，根据Kapitaniak定义，此时系统不会发生Kapitaniak定义下的随机混沌。

综上可得，不管在颤振前区还是颤振后区，受外部随机激励的影响系统动态特性都会发生突变、发生分岔，甚至进入混沌运动状态。但也会在一定随机扰动强度下从混沌运动状态突变回周期运动。因此，在进行二元机翼气动弹性特性研究时，要考虑不同飞行环境状态的影响，避免系统发生复杂动力学行为。

5 数值计算验证

为了验证分析结果的有效性，现采用数值方法对分析结果进行验证。首先采用Monte Carlo模拟法对随机激励进行模拟，然后利用与前文一致的参数取值，在MATLAB平台上对状态方程(4)进行数值求解。不同工况下系统的时域响应曲线、庞加莱截面图如图6、图7所示，系统的最大Lyapunov指数随来流马赫数Ma的变化曲线，如图8所示。

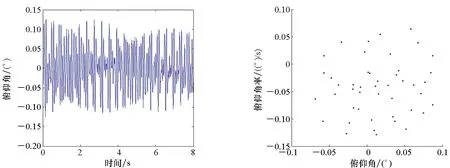
(a) 俯仰角时程曲线(D=0.01)(a) Time history curve of pitch angle(D=0.01) (b) 庞加莱截面(D=0.01)(b) Poincare section(D=0.01)

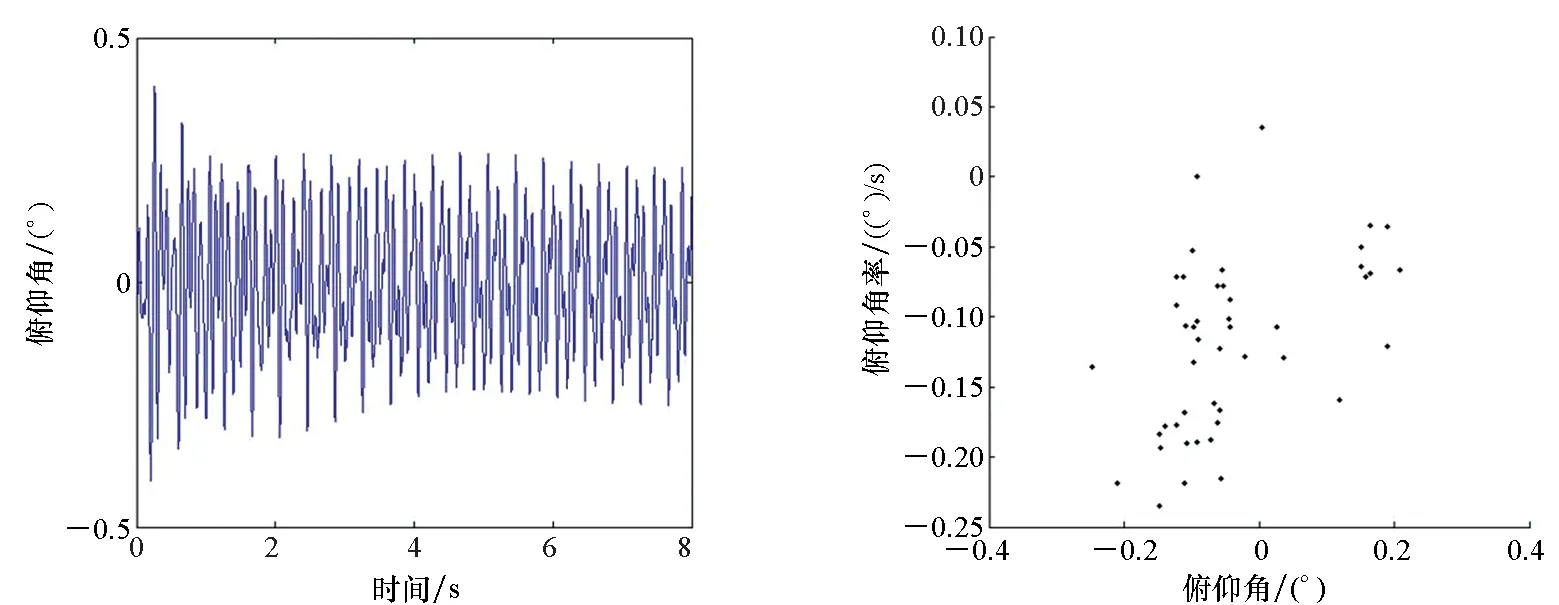
(c) 俯仰角时程曲线(D=0.1)(c) Time history curve of pitch angle(D=0.1) (d) 庞加莱截面(D=0.1)(d) Poincare section(D=0.1)图6 不同扰动强度下颤振前区的系统响应曲线及庞加莱截面(Ma=3)Fig.6 Response of the system with various disturbance intensities and Poincare section(Ma=3)

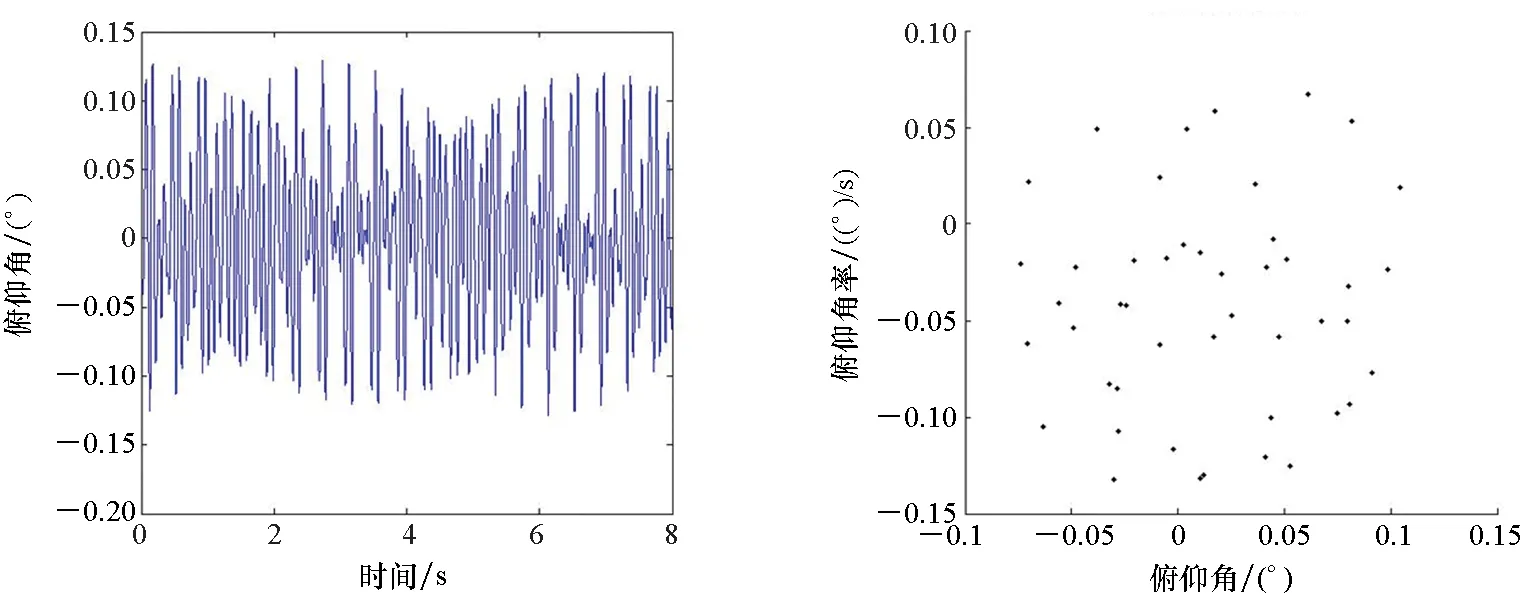
(a) 俯仰角时程曲线(D=0.01)(a) Time history curve of pitch angle(D=0.01) (b) 庞加莱截面(D=0.01)(b) Poincare section(D=0.01)

(c) 俯仰角时程曲线(D=0.1)(c) Time history curve of pitch angle(D=0.1) (d) 庞加莱截面(D=0.1)(d) Poincare section(D=0.1)图7 不同扰动强度下颤振后区的系统响应曲线及庞加莱截面(Ma=5)Fig.7 Response of the system with various disturbance intensities and Poincare section(Ma=5)

(a) D=0.01

(b) D=0.1

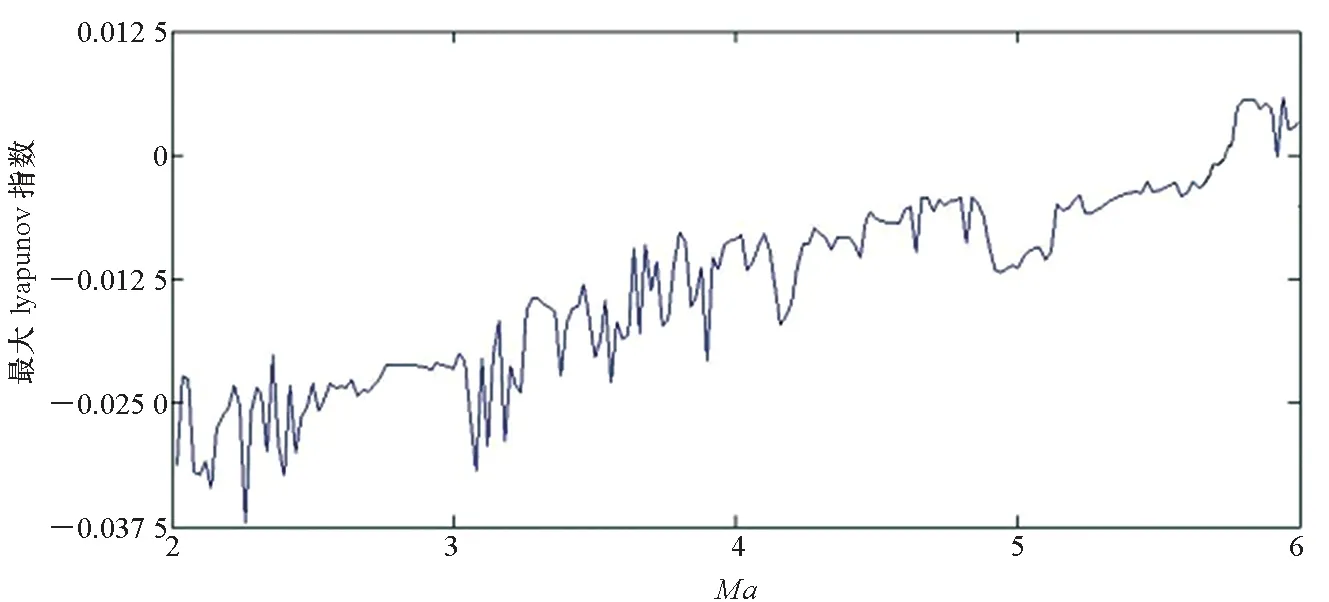
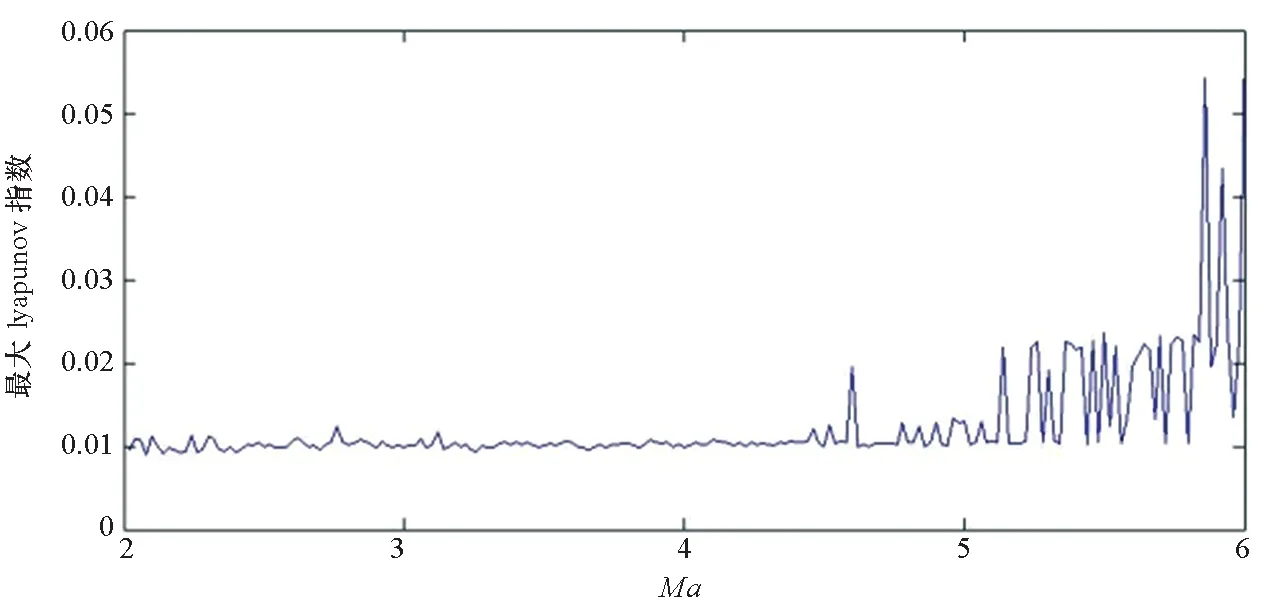
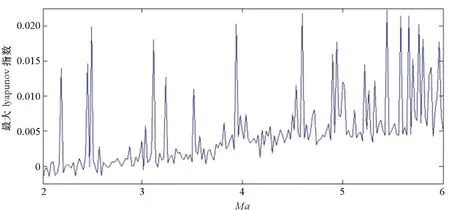
(c) D=0.5图8 最大lyapunov指数变化曲线图Fig.8 The largest lyapunov exponent changes with Ma

从图6～8可以看出，在弱随机扰动、一般随机扰动强度作用下，无论是颤振前区还是颤振后区，系统的俯仰角随时间均呈无规律变化，同时庞加莱截面由分形结构的大量散点组成，且系统在Ma=3、Ma=5时最大Lyapunov指数均为正值，说明系统进入了混沌运动状态；而在随机扰动强度为0.5时，系统在Ma=3、Ma=5时最大Lyapunov指数均为负值，说明系统未进入混沌运动状态，验证了前文中Kapitaniak定义下的随机混沌分析结果，说明了本文近似解析定性分析方法的准确性和有效性。

6 结论

本文通过累积量截断法、非高斯截断法及Edgeworth展式等获得系统的联合概率密度函数，在Kapitaniak定义下研究了二元机翼的随机混沌特性，并通过数值方法对计算结果进行验证。主要研究结果如下：

1)采用第二类拉氏方程建立二元机翼随机非线性动力学方程，并通过三阶活塞理论推导二元机翼的非线性气动力和气动力矩。通过中心流形定理对系统进行降维，将2自由度下4维非线性系统的动力学方程成功降为2维，使系统的随机非线性动力学特性研究得到简化。

2)采用累积量截断法和非高斯截断法获得系统二维联合概率密度函数，利用Kapitaniak定义判断系统的随机混沌特性。研究发现，当随机扰动强度为0.01和0.1时，系统在颤振前区和颤振后区均进入了混沌运动状态；在随机扰动强度为0.5时，系统没有进入混沌运动状态。这说明外部随机扰动对系统具有很大影响。因此，在二元机翼气动弹性特性控制时，必须充分考虑外部随机激励强度的影响，以增加系统的稳定性和安全性。

3)通过时域响应曲线、庞加莱截面图和最大Lyapunov指数等数值方法对计算结果进行验证，两种具有较好的一致性，说明本文研究具有较高的研究精度。