均匀圆阵主特征矢量分析解相干算法*

倪柳柳，陈 辉，倪萌钰，王晓戈

(空军预警学院， 湖北 武汉 430019)

波达方向(Direction-Of-Arrival, DOA)估计一直是无线电通信、电子对抗侦察、声呐以及雷达系统等诸多领域的一个重要问题，在进行DOA估计之前需要确定阵列形状，常用阵型有均匀线阵(Uniform Linear Array，ULA)、L型阵列及均匀圆阵(Uniform Circular Array，UCA)等，其中，均匀圆阵因其可提供360°的全方位无模糊定位以及各向同性性质而越来越得到重视。同时在实际波达方向估计中，由于反射或折射等引起的传输多径现象，或敌方设置的有源电磁干扰等，相干信号广泛存在，因此对于相干信号的检测与估计也是DOA估计中的重要研究方向。因此本文将研究适用于均匀圆阵的解相干算法。

目前，适用于均匀圆阵的解相干算法主要有三大类。一是虚拟阵变换，其思想就是通过阵列变换将圆阵转换为虚拟均匀线阵[1-3]或者多个相同间距的均匀圆阵[4-6]，然后再利用空间平滑等方法进行解相干处理。如模式空间平滑(Method Of Direction Estimation-Space Smoothing, MODE-SS)算法[1]，就是将均匀圆阵通过模式空间变换转换成一个同孔径等距均匀线阵，再进行空间平滑处理。模式空间托普利兹(Method Of Direction Estimation-TOEPlitz, MODE-TOEP)[2]是在模式空间变换后重构一个Toeplitz矩阵，这个矩阵的秩只和DOA信息有关，因此可以解相干。而模式空间差分(Method Of Direction Estimation-DIFFerence, MODE-DIFF)[3]算法将MODE-TOEP算法和差分算法相结合，达到同时估计非相关和相干信源的目的。模式空间中心对称(Method Of Direction Estimation-Central Symmetry, MODE-CS)[5]利用均匀圆阵的中心对称性对模式空间数据进行共轭平均，通过相关性构造Hermitian Toeplitz矩阵，实现圆阵相干信源的方位估计。这类算法的优点是解相干的信号源数较多；但其缺点为阵列的变换会带来误差，导致DOA估计精度不高。二是采用多维搜索类算法[7-11]进行估计。这类算法不需要进行解相干预处理，就可以直接进行DOA估计，如基于轮换投影的最大似然(Alternative Projection-Maximum Likelihood, AP-ML)算法[10]、加权信号子空间拟合(Weighted Signal Subspace Fitting, WSSF)算法[8,11]等。这类算法的优点就是算法的估计精度高；缺点是运算过程中要用到多维搜索，运算量巨大。三是稀疏重构类DOA算法[12-18]，这类算法利用恢复稀疏信号的思想进行算法设计。Malioutov等将DOA估计算法转变为基于L1范数的优化问题，提出了基于L1范数的奇异值分解(L1-Singular Value Decomposition, L1-SVD)算法[12]；文献[13]中的基于L1范数的矩阵协方差稀疏重构(L1-Sparse Representation of Array Covariance Vectors, L1-SRACV)算法利用了协方差矩阵的稀疏特性，并通过求解二阶锥优化问题来实现DOA估计；Yang等则提出了离格稀疏贝叶斯(Off Grid-Sparse Bayesian Inference, OG-SBI)DOA估计方法[14-15]，也就是首先设置较粗的网格，而在估计过程中通过不停迭代将真实信源附近的网格不断逼近真实角度，最终实现DOA估计。这类算法的优点是无须信源数信息，对相干信源不敏感，估计精度较高。缺点为算法都是有偏估计，其DOA估计值相对真实值的偏差取决于网格的划分，而网格划分太小的话复杂度将非常高。

近年来，一种基于均匀线阵的新的解相干DOA算法[19-20](Principal-eigenvector Utiliztion for Modal Analysis, PUMA)被提出，该算法利用均匀线阵具备的范德蒙德结构来设计DOA算法，能够较好地估计相干信源的DOA。受此启发，本文提出了一种基于虚拟均匀线阵的主特征矢量分析算法(Virtual uniform Linear array Principal Eigenvector Analysis，VLPEA)，算法在模式空间变换的基础上，分析虚拟均匀线阵主特征矢量的特性，通过求解线性预测算子最终成功估计出信源的方向。下节的分析和实验证明了本文算法估计精度高，复杂度低。

1 均匀圆阵阵列模型及预处理

本文采用均匀圆阵为阵列模型，其结构如图1所示。

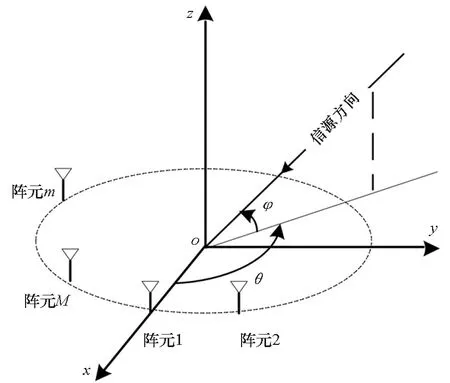
图1 均匀圆阵阵列模型Fig 1 Array model of UCA

M个各向同性的阵元均匀分布在半径为r的圆阵上，远场窄带相干信号以方位角度θ和俯仰角度φ入射到各个阵元，θ为信源和阵列中心的连线在xoy面上的投影与x轴的夹角，φ为信源和阵列中心连线与xoy平面之间的夹角，其中θ∈[0,2π]，φ∈[0,π]。

假设空间有K个波长为λ的远场窄带信号入射到UCA上，以阵列中心为参考点，第m个阵元位置为pm=(xm,ym,0)，xm=rcosψm，ym=rsinψm，ψm=2π(m-1)/M，ψm为第m个阵元和圆心连线与x轴的夹角，第k个信号坐标为γk=(cosφkcosθk,cosφksinθk,sinφk)，因此阵列模型导向矢量为

a(θk,φk)=[e-jω0τ1k，e-jω0τmk，…,e-jω0τMk]T

(1)

式中：τmk=cosφkcos(θk-ψm)r/c为第k个信号在第m个阵元相对于参考阵元的时延k∈[1,K]；ω0=2πc/λ，c为光速，λ为信号波长。因此流型矩阵为

A=[a(θ1,φ1),a(θk,φk),…,a(θK,φK)]

(2)

第t次快拍时的接收数据矢量为

x(t)=As(t)+n(t),t=1,…,N

(3)

式中，x(t)∈CM，u(t)∈CK和n(t)∈CM分别表示第t快拍数下的阵列接收数据、信源矢量和噪声矢量，N为总快拍数。

本文只讨论所有信源与xoy平面共面的情况，此时φk=0，接收数据变为

x(t)=ACs(t)+n(t)

(4)

式中，AC(θ)=[aC(θ1),aC(θ2),…,aC(θK)]，导向矢量aC(θk)=a(θk,0)。

综上可知，均匀圆阵的阵列流形矩阵不符合范德蒙德结构，大部分解相干DOA估计方法并不适用，因此考虑利用模式空间变换法将阵列流型进行变换，得到符合范德蒙德结构的阵列流型，为下一步的解相干奠定基础。构造模式空间变换矩阵为

(5)

式中：J=diag{j-QJ-Q(-β),…,jQJQ(-β)}，Jq(-β)为q阶第一类贝塞尔函数，β=2πr/λ，Q=⎣β」为均匀圆阵可以激发的最大相位模式，这里⎣·」表示向下取整；F=[w-Q,w-Q+1，…,wQ]，wq=[1,e-j2πq/M,…,e-j2πq(M-1)/M]，q=-Q,…,Q。

当取M>2h+1时，可以用构造的模式空间变换矩阵得到模式空间中虚拟均匀线阵的接收数据矢量：

(6)

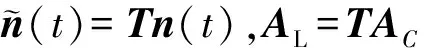
(7)

从式(7)可以看出，变换后的阵列流型具有范德蒙德结构，即等效为阵元数为D=2Q+1的虚拟均匀线阵，变换后的阵列数据协方差矩阵为

(8)

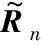
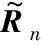
(9)

由式(9)可知，模式变换后的各通道噪声功率不一致，因此必须使用广义特征分解求解子空间。设λd(d=1,2,…,D)为矩阵束(RL,TTH)广义特征分解后得到的所有特征值,按从大到小排列，ud为对应的特征矢量，前P个大特征值对应的主特征矢量组成矩阵ULS=[u1,u2,…,uP]，假设有K1个相干信源，则P=K-K1+1，但是其张成的子空间并不是虚拟线阵的信号子空间，对其进行进一步的处理，得到修正的主特征矢量矩阵：

VS=TTHULS

=[v1,v2,…,vP]

=[TTHu1,TTHu2,…,TTHuP]

(10)

同上可得修正的噪声子空间：

Vn=[vP+1,vP+2,…,vD]

=[TTHuP+1,TTHuP+2,…,TTHuD]

(11)

2 虚拟均匀线阵主特征矢量分析算法

由文献[21]证明：

span(VS)=span(AL)

(12)

式(12)表明信号子空间VS和虚拟线阵的流行矩阵张成同一空间，而AL具有范德蒙德结构，因此考虑利用线性预测(Linear Prediction, LP)算法的原理，即vk(k=K+1,K+2,…,P)中任一元素和此元素之前K个元素线性相加为0，来求解线性系数对应的角度。

2.1 算法推导

根据LP原理，得到

(13)

式中，[vk]l为vk中第l个元素，ci为之前第i个元素对应的LP系数。因此第k个角度θk包含在如下多项式中：

(14)

式中，zk=ejθk。式(13)用矩阵形式可以表示为

Gkc=hk

(15)

式中

(16)

c=[c1,c2,…,cK]T

(17)

hk=-[[vk]K+1,[vk]K+2,…,[vk]D]T

(18)

Gc=h

(19)

式中

(20)

(21)

令εk=Gkc-hk，可以得到

(22)

显而易见，理想情况下，式(19)是经典线性系统，可以用最小二乘(Least Squares, LS)法求解c，其闭式解为

cLS=G†h

(23)

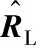
(24)

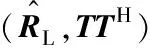
(25)

同理得

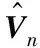
(26)

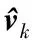
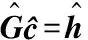
(27)

(28)

式中

(29)

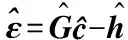
(30)

在无误差条件下

ε=vec([ε1,ε2,…,εP])=vec(B(c)VS)=0(D-K)P

(31)

式中

(32)

其中，toep(a,b)表示由向量a和b构成的Toeplitz矩阵，然后将误差考虑进去，式(31)变为

(33)

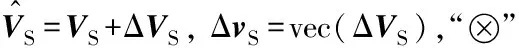
(34)

文献[19]指出主特征矢量误差之间具有如下特性：

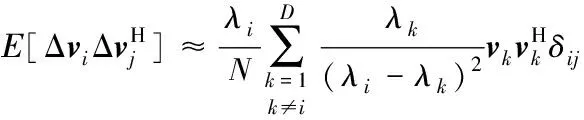
(35)

式中，δij为冲激函数。由式(35)可得

(36)

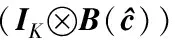
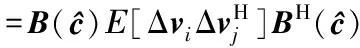
(37)

由式(34)、式(36)和式(37)得

(38)

(39)

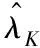
(40)

(41)

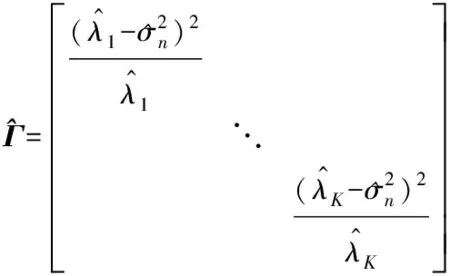
(42)

(43)

2.2 算法流程

综上所述本文提出VLPEA算法，算法步骤如下所示。

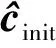
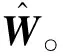
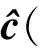
(44)

式中，“∠”为求角度符号

2.3 算法分析

MODE-TOEP算法利用协方差矩阵的某一列重构具有Toeplitz结构的矩阵，因此可以估计相干信源，然而也是因为上述重构方法，其信息利用并不充分，因此其估计精度无法达到最佳。MODE-DIFF算法使用了差分算法分别估计相干信源和独立信源，然而差分的同时也去掉了分相干信源的部分信息，因此同样无法将估计精度提升到最优。改进特征分解(Excitation Mode EigenValue Decomposition, EMEVD)算法[21]是在上述两种算法的基础之上再加上一次特征分解，同样无法解决信息利用不全的问题。而本文的VLPEA算法通过对式(16)进行WLS求解，该矩阵包含了信源的所有信息，因此本文算法精度要比EMEVD算法、MODE-TOEP算法和MODE-DIFF算法高，同时文献[19]证明了式(19)的WLS代价式在信噪比或者快拍数趋近于无穷大时可以等价于ML算法，因此VLPEA算法估计精度很高。

3 仿真与分析

为验证VLPEA算法的有效性，本节使用MATLAB进行如下仿真实验，所有实验均采用15阵元的均匀圆阵阵列结构(即M=15)，阵元半径为0.7倍的波长。在仿真实验中，将本文算法与MODE-TOEP算法、MODE-DIFF算法、MODE-CS算法，ML算法以及OG-SBI算法做比较，其中ML算法采用文献[10]中的AP-ML算法，OG-SBI算法中的终止迭代条件为ξ≤1×10-6，最大重复迭代次数为1 000，初始网格为2°。在单次实验中每个真实角度与估计角度的偏差小于0.4倍的相邻两角度间隔时，则认定为算法分辨成功，完全均方根误差(Completed Root Mean Squared Error, CRMSE)定义为成功分辨DOA信号的均方根误差(Root Mean Square Error, RMSE)，如式(45)所示。

(45)

3.1 实验1： 比较算法在信噪比变化时的性能

实验1比较了不同算法的CRMSE和分辨概率随信噪比变化的性能改变情况。假设有4个等功率信号入射到阵列上，DOA分别为θ1=10°，θ2=25°，θ3=50°，θ4=70°，前两个信号源相干，快拍数取200，信噪比(Signal to Noise Ratio, SNR)的变化范围为-5～20 dB，步长为2 dB，进行2 000次蒙特卡洛独立重复实验，实验结果如图2所示。从图2(a)可以看出，ML算法的信源CRMSE是最小的，本文提出的VLPEA算法的性能要比EMEVD算法、MODE-TOEP算法、MODE-CS算法和MODE-DIFF算法好，这与上文的分析是一致的，同时在信噪比小于15 dB时，VLPEA算法的CRMSE比OG-SBI算法小，当信噪比更大时OG-SBI算法性能则有所提升。由图2(b)可以看出，当SNR大于1时，VLEPA算法的成功概率达到100%，而OG-SBI、EMEVD算法、MODE-TOEP算法和MODE-DIFF算法的成功概率在SNR大于10时才能达到100%。

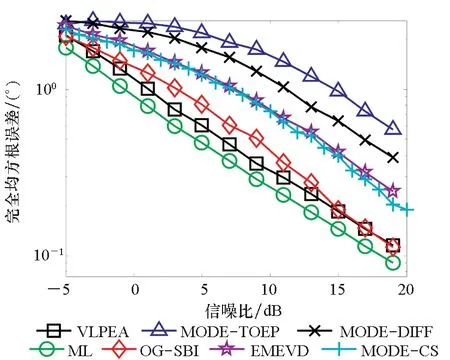
(a) 不同DOA估计算法CRMSE随信噪比SNR变化(a) CRMSE of different DOA estimationalgorithms versus SNR

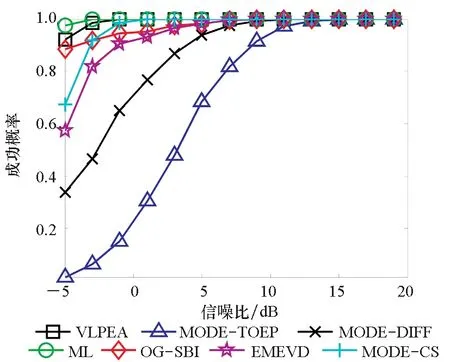
(b) 不同算法的DOA估计成功概率随信噪比SNR变化(b) Success probability of different DOA estimation algorithms versus SNR图2 不同信噪比情况下的算法性能分析Fig 2 Performance analysis of the algorithms under different SNR

3.2 实验2： 比较算法在快拍数变化时的性能

图3显示的是不同算法的CRMSE和成功概率随快拍数变化的情况，SNAP即为快拍数，此实验中SNR固定为20 dB，快拍数变化范围为20～300，步长为20次快拍数，其他参数的设定和实验1一致。可以看出，随着快拍数的增加， VLPEA算法和其他几种算法的CRMSE都呈现降低的趋势，其中依然是ML算法的CRMSE始终最小，OG-SBI算法其次，VLPEA算法的CRMSE十分接近上述两种算法，而EMEVD算法、MODE-TOEP算法、MODE-CS算法和MODE-DIFF算法的CRMSE则比上述三种算法大接近一个数量级，在图3(b)中，MODE-TOEP算法和MODE-DIFF算法同样需要较多的快拍数才能保持性能稳定。

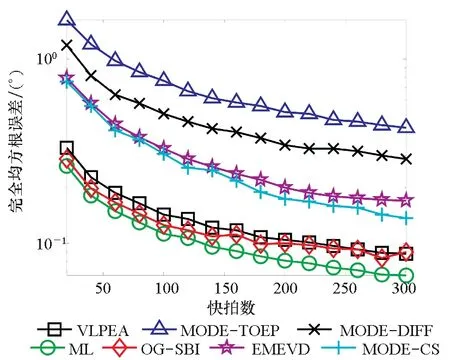
(a) 不同算法的DOA估计CRMSE随快拍数SNAP的变化(a) CRMSE of different DOA estimation algorithms versus SNAP

3.3 实验3： 比较算法在角度间隔变化时的性能

本次实验比较各个算法的分辨性能。设定信噪比为20，快拍数为200，两个相干信源入射到阵列上，第一个角度θ1固定为10°，第二个角度θ2从12°变化到30°，其他参数和前面的实验一致，结果如图4所示。图4的横坐标为两个角度的间隔变化，由图4(b)可以看出，在角度间隔大于5°时，ML算法和VLPEA算法的成功概率能到100%，而EMEVD算法、MODE-TOEP算法、MODE-CS算法和MODE-DIFF算法在信噪比大于10时成功概率才能到100%，因此图4(a)观察所有算法成功概率等于100%时的CRMSE，发现ML算法、OG-SBI算法以及VLPEA算法的CRMSE都维持在一个比较低的水平。

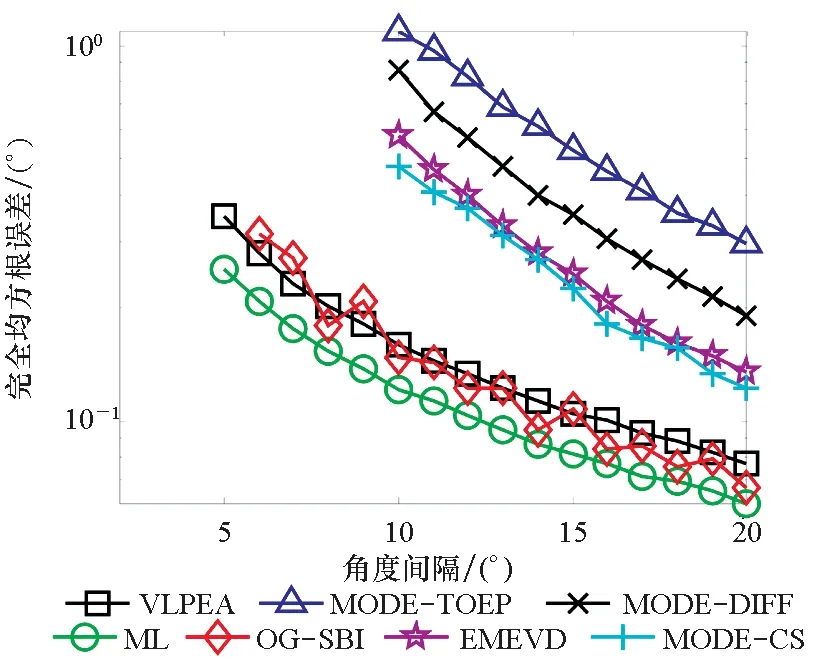
(a)不同算法的DOA估计CRMSE随角度间隔的变化(a) CRMSE of different DOA estimationalgorithms versus spacing

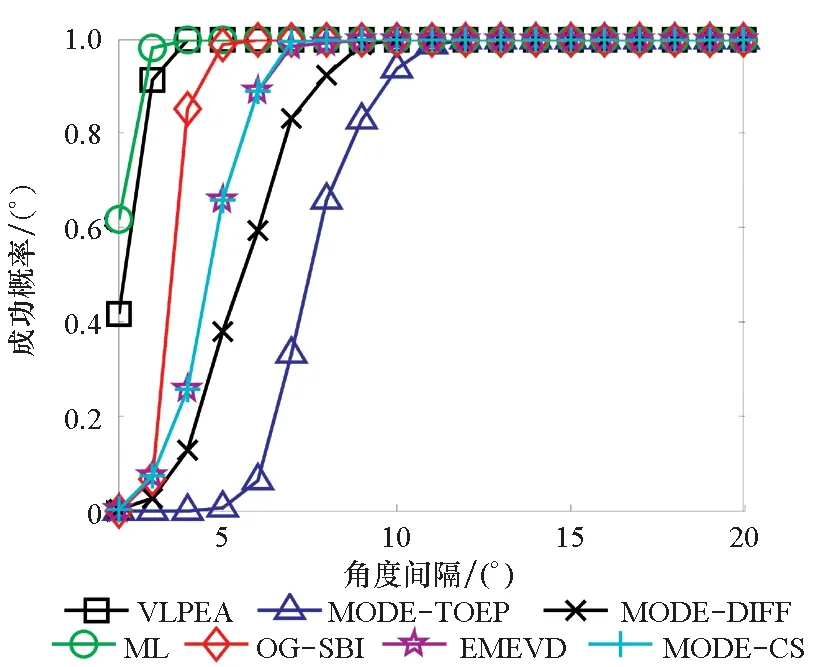
(b) 不同算法的DOA估计成功概率随角度间隔的变化(b) Success probability of different DOA estimation algorithms versus spacing图4 不同角度间隔下的算法性能分析Fig.4 Performance analysis of the algorithms under different spacing

3.4 实验4： 算法的时间复杂度分析

本次实验比较各个算法的时间复杂度。快拍数固定为200，两个入射角度分别为10°和25°，信噪比固定为20，阵元数不变，表1所示为不同算法在阵元数变化时的单次平均运行时间，可以看出OG-SBI算法的耗时相当长，这是因为为达到较高的精度，其算法中的迭代门限取得很小，导致重复次数非常高， ML算法也需要大约1 s才能完成DOA估计，而EMEVD算法、MODE-TOEP算法、MODE-DIFF算法，MODE-CS算法以及VLPEA算法都能在极短时间内分辨出信源，且VLPEA算法运算时间最短，达到了毫秒级，说明了VLPEA算法的计算量很低，与前文的分析一致。

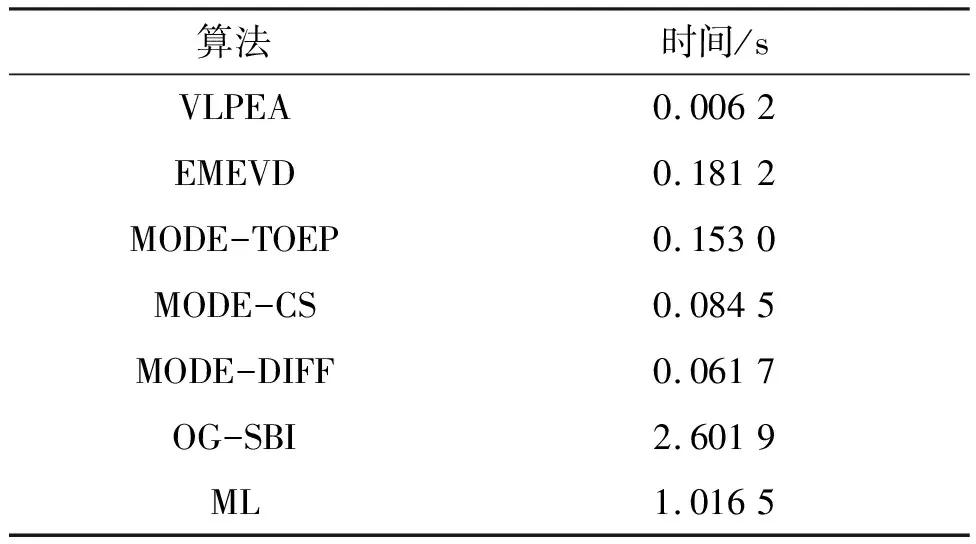
表1 不同算法单次平均运行时间比较

4 结论

本文提出了一种均匀圆阵的相干信源波达方向估计算法——VLPEA算法。该算法首先通过模式空间变换技术将均匀圆阵转换为模式空间中的虚拟均匀线阵，在此基础上对其数据协方差矩阵广义特征分解，得到新的主特征矢量矩阵；其次根据均匀线阵的范德蒙德结构，构造包含信源DOA信息的线性多项式；最后通过加权最小二乘法重复迭代得到线性预测系数成功求得相干信源的波达方向。

通过理论分析和仿真结果，可以得出VLPEA算法的估计精度明显优于MODE-TOEP和MODE-DIFF算法，且与ML算法和OG-SBI算法接近，但是复杂度远低于上述两种算法，因此VLPEA算法具有较好的估计精度、分辨力且实时估计更可靠。