精密RV减速器受力分析
项兆森 郑鹏


摘要:机器人RV减速器中摆线轮,轴承是RV减速器的重要零部件,其受力大小有较大影响。以RV-80E 减速器为研究对象,对摆线轮与摆线轮支撑轴承,进行受力分析计算,并使用UG软件进行运动仿真,验证其受力准确性。得出轴承受力与曲柄轴角度,摆线轮针齿受力变化曲线,为相关研究 RV 减速器零件的优化分析和应用提供了数据支持。
Abstract: In RV Reducer, cycloid wheel and bearing are important parts of RV Reducer, and their force has great influence. Taking rv-80e reducer as the research object, the force analysis and calculation of cycloid wheel and cycloid wheel support bearing are carried out, and the motion simulation is carried out by using UG software to verify the force accuracy. The curves of bearing force and cycloid angle, cycloid force and revolution angle are obtained, which provide data support for the optimization analysis and application of RV Reducer parts.
關键词:RV减速器;零件;受力分析
Key words: RV Reducer;parts;stress analysis
中图分类号:TH132.46 文献标识码:A 文章编号:1674-957X(2021)09-0047-03
0 引言
我国目前是世界上最大的工业生产国和消费大国,对工业机器人的需求量逐年增长,根据国际机器人联合会(IFR)发布的“2020年全球工业机器人报告”中指出。尽管2020年新冠肺炎病毒大流行对全球经济造成的严重的后果,但全球工厂中运行的工业机器人仍然达到270万台,同比增长了12%。中国的运营存量在2019年增长了21%,达到约78.3万台[1]。在此大背景下,以工业机器人技术为核心的智能制造技术是我国高端制造和智能制造产业发展的主要方向,RV传动作为一种新型传动广泛应用于工业制造装备中,尤其是工业机器人领域[2],因此对工业机器人精密减速器关键零部件制造技术进行深入研究,具有重要意义和价值[3]。
1 RV减速器介绍
RV减速器具有小型、轻量、刚度大、寿命长、传动精度高且平稳等一系列优点,在工业机器人领域被广泛应用[4]传动过程中,RV减速器通过俩级减速,输入行星齿轮副完成一级减速部分。摆线轮,针齿和行星架组成摆线针轮副完成二级减速部分,来达成较大减速比。传动简图如图1所示。
RV减速器主要由1、输入轴,2、行星轮,3、曲柄轴,4、摆线盘,5、针齿,6、输出盘等组成[5]。
2 摆线轮针齿啮合传动的受力分析
本文以RV-80E减速器为对象,其额定转速15r/min,额定扭矩为800N.m。传动比为121,其基本参数表1所示。
在实际工作中RV减速器的摆线轮多需要进行修形,这样会使传动更加平稳顺滑,传动误差更小,所以要考虑修形对摆线轮和针齿之间的啮合力的影响。因此摆线轮轮齿与针齿之间的部分齿会有初始间隙的产生,其初始间隙Δ(ψi)根据文献[6]公式如下。
式中,Ψi为第i个针齿相对于转臂的转角,a=0.008为移距修型量,b=0.004为等距修型量,k为短幅系数,k=ezp/rz,e为曲柄轴偏心距。
根据赫兹公式,俩圆柱接触变形通过式求解:
式中,F为摆线轮针齿两圆柱的接触作用力,E1、E2为其弹性模量,R1、R2为两圆柱半径,μ1、μ2为圆柱的泊松比,b 通过式确定:
摆线轮实际齿廓曲线的曲率半径为ρ,且当曲率大于半径时,摆线轮齿廓是凹的,当曲率小于半径时,摆线轮齿廓是凸的。如下式(4)-式(5)表示。
求出各个位置处的摆线轮和针齿之间的变形和针齿与针齿壳之间的变形,相加得到啮合力为接触方向上的综合变形。把所有变形量求出能得到最大变形量Wmax。在弹性变形条件下,啮合力法向上的位移计算如下式:
当δi-ΔΨi?叟0时,相应的针齿与摆线轮啮合,计算可知啮合齿数为19个,摆线轮与针齿啮合力的计算如式(6)-式(8)所示:
上式中r'c=ezc,p、t表示的是针齿与摆线轮啮合的齿号,表示从第p个齿开始啮合,到第t个齿结束啮合。从公式(2)和(8)中可以看出,若要想求得针齿的最大弹性变形量δmax就需要先得出最大啮合力Fmax,但要求解出得最大啮合力Fmax又需要先求出最大弹性变形量δmax,因此这就需运用迭代的方法。首先给定一个初始值Fmax0如式(9)并代入公式(11),当Fmax-Fmax0小于0.01Fmax时,停止迭代,得到啮合合力及每个针齿与摆线轮之间的啮合力。
方法具体流程如图2所示。
经历迭代后满足条件的最大初始力Fmax0=709.95N。由接触理论计算公式可知,计算摆线轮和针齿两个圆柱体之间接触应力的公式,如式(10)所示:
上式中,Ed是2倍的针齿弹性模量,摆线轮弹性模量的乘积与相加和的差积。称为当量弹性模量。le为摆线轮与针齿接触的有效长度;pi为当量曲率半径,,ρi为啮合点处摆线轮曲率半径。有19个针齿参与啮合,摆线轮针齿间的啮合力及应力如表2所示。
根据上述数据可知摆线轮与针齿最大啮合力发生在3号针齿处,而2号针齿啮合应力最大。导致这一现象的原因是摆线轮的齿廓形状凹凸不平与针齿接触啮合造成的。通过啮合齿各个齿啮合力可以得到针齿对摆线轮的啮合合力。
3 曲柄轴支撑轴承的受力分析
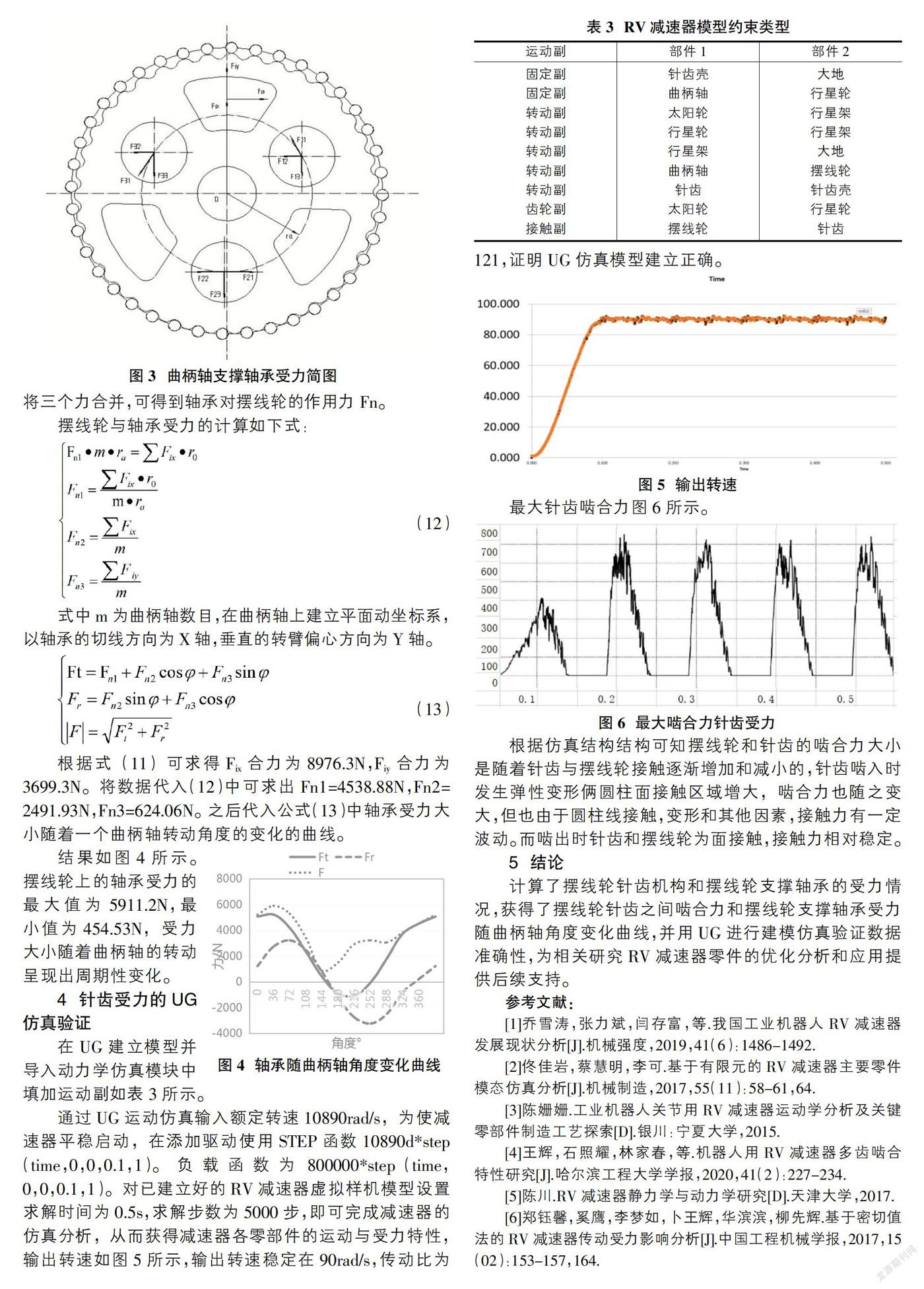
曲柄轴支撑轴承对摆线轮的合力分为Fn1、Fn2、Fn3三个部分。其中Fn1的合力对O产生力矩平衡切向作用力FiX的对O产生力矩,Fn2与Fix合力相平衡,Fn3与Fiy合力相平衡。假如负载保持恒定,Fn1的方向相对曲柄轴不变,大小不变;Fn22与Fn3的大小相对也不发生变化,方向随着曲柄轴的自转而发生改变,因此Fn1为摆线轮的轴承上保持不变的载荷,Fn2与Fn3为曲柄轴转动的旋转载荷,将三个力合并,可得到轴承对摆线轮的作用力Fn。
摆线轮与轴承受力的计算如下式:
式中m为曲柄轴数目,在曲柄轴上建立平面动坐标系,以轴承的切线方向为X轴,垂直的转臂偏心方向为Y轴。
根据式(11)可求得Fix合力为8976.3N,Fiy合力为3699.3N。将数据代入(12)中可求出Fn1=4538.88N,Fn2=2491.93N,Fn3=624.06N。之后代入公式(13)中轴承受力大小随着一个曲柄轴转动角度的变化的曲线。
结果如图4所示。摆线轮上的轴承受力的最大值为5911.2N,最小值为454.53N,受力大小随着曲柄轴的转动呈现出周期性变化。
4 针齒受力的UG仿真验证
在UG建立模型并导入动力学仿真模块中填加运动副如表3所示。
通过UG运动仿真输入额定转速10890rad/s,为使减速器平稳启动,在添加驱动使用STEP函数10890d*step(time,0,0,0.1,1)。负载函数为800000*step(time,0,0,0.1,1)。对已建立好的RV减速器虚拟样机模型设置求解时间为0.5s,求解步数为5000步,即可完成减速器的仿真分析,从而获得减速器各零部件的运动与受力特性,输出转速如图5所示,输出转速稳定在90rad/s,传动比为 121,证明UG仿真模型建立正确。
最大针齿啮合力图6所示。
根据仿真结构结构可知摆线轮和针齿的啮合力大小是随着针齿与摆线轮接触逐渐增加和减小的,针齿啮入时发生弹性变形俩圆柱面接触区域增大,啮合力也随之变大,但也由于圆柱线接触,变形和其他因素,接触力有一定波动。而啮出时针齿和摆线轮为面接触,接触力相对稳定。
5 结论
计算了摆线轮针齿机构和摆线轮支撑轴承的受力情况,获得了摆线轮针齿之间啮合力和摆线轮支撑轴承受力随曲柄轴角度变化曲线,并用UG进行建模仿真验证数据准确性,为相关研究RV减速器零件的优化分析和应用提供后续支持。
参考文献:
[1]乔雪涛,张力斌,闫存富,等.我国工业机器人RV减速器发展现状分析[J].机械强度,2019,41(6):1486-1492.
[2]佟佳岩,蔡慧明,李可.基于有限元的RV减速器主要零件模态仿真分析[J].机械制造,2017,55(11):58-61,64.
[3]陈姗姗.工业机器人关节用RV减速器运动学分析及关键零部件制造工艺探索[D].银川:宁夏大学,2015.
[4]王辉,石照耀,林家春,等.机器人用RV减速器多齿啮合特性研究[J].哈尔滨工程大学学报,2020,41(2):227-234.
[5]陈川.RV减速器静力学与动力学研究[D].天津大学,2017.
[6]郑钰馨,奚鹰,李梦如,卜王辉,华滨滨,柳先辉.基于密切值法的RV减速器传动受力影响分析[J].中国工程机械学报,2017,15(02):153-157,164.
作者简介:项兆森(1997-),男,辽宁营口人,硕士研究生,研究方向为机械工程与自动化;郑鹏(通讯作者)(1964-),男,辽宁辽阳人,博士,教授,研究方向为现代制造技术与测量、数控制造技术、机械成套设备设计与开发等。

