数据驱动下孪生贝叶斯理论非齐次泊松过程的结构损伤评估方法
朱林 陈敏 贾民平 冯月贵 庆光蔚


摘要: 以结构件裂纹扩展过程中的损伤状态评估为研究对象,提出了一种孪生贝叶斯理论非齐次泊松过程的结构损伤评估方法。首先,結合基于裂尖场能量的可靠度序化策略与非齐次泊松过程,运用贝叶斯理论对试验信息及总体过程参数的渐进关系进行组合,获得过程参数先验分布。同时,基于裂尖场能量递进因子与似然函数的概念,通过先验信息、序化策略及后验信息的组合,建立了孪生贝叶斯理论非齐次泊松过程的参数后验分布模型。最后以典型结构为例,结合声发射检测到的裂纹扩展数据对提出方法的可行性进行验证,并将预测结果与独立的试验结果进行比较。结果表明,提出方法的平均预测精度为92.1%,可以实现通过少量试验信息完成不同初始损伤状态下结构件损伤状态评估的目的。
关键词: 损伤评估; 递进因子; 非齐次泊松; 序化策略; 贝叶斯
中图分类号: TB123 文献标志码: A 文章编号: 1004-4523(2021)01-0134-07
DOI:10.16385/j.cnki.issn.1004-4523.2021.01.015
引 言
随着装备向大型化发展,其最大装载吨位也不断提高,微小的裂纹就可能造成巨大的危害。因此,裂纹结构的损伤评估已成为这一领域的研究重点[1?2]。
一般情况下,评估对象能做的试验次数较少,如何利用经验来减少试验就极为关键,这一点也推动了贝叶斯理论的应用。Torregosa等[3]根据裂纹扩展中不同输入参数对评估结果的影响,建立了动态贝叶斯模型。Beck等[4]根据结构损伤服从指数与Weibull分布的特点,建立了基于贝叶斯理论的结构损伤状态评估方法,并对其可行性与分析准确性进行了验证。Luque等[5]以结构损伤为分析对象,通过更新策略来融合先验与后验信息,完成了典型结构的寿命预测。赵申坤等[6]针对系统可靠性问题,提出了一种基于数据驱动和贝叶斯理论的剩余寿命预测方法。为了提高结构损伤评估的效率,完成同一批结构的评估是必要的。大多情况下,同一批构件间的初始状态是不同的,这给同一类结构的高效评估带来了困难。文献[3?6]基本上能够实现先验信息与后验信息的传递,但评估模型的假设都具有相同的初始状态,无法适用于评价同一批结构。
鉴于此,本文提出了孪生贝叶斯理论非齐次泊松过程的结构损伤评估方法,建立序化策略,并将试验信息及递进因子进行组合,获得非齐次泊松过程(Non?homogeneous Poisson Process,NHPP)的参数先验分布,并结合似然函数,求解参数后验分布,来评估不同裂纹初始状态下的结构损伤状态。
1 基于裂尖场能量的可靠度序化策略
然后在图5所示的应力状态分布结果中由高应力值向低应力值布置积分路径,假设距离为0处是分析结构的应力最大值点位置。拟合图5中裂尖场所对应的应力状态分布方程,并将其与距离为0处的最大应力值代入式(2)中对裂尖场能量进行求解,最后将不同初始状态下的裂尖场能量代入式(1)可得到如表4中所示的裂尖场能量递进因子。
将标准载荷1000 N、材料力学参数代入式(5)的预测模型中,对多组表面质量系数与加载方式系数的数据组合所对应的裂纹扩展长度进行求解。然后运用Weibull过程对尺寸参数与形状参数进行求解,获得如表5所示的尺度参数与形状参数的均值与标准差。
根据递进关系得到如表4所示的先验尺度参数与形状参数。同时,根据先验尺度参数与先验形状参数对先验系数进行求解。由于数据组1的先验估计过程中对构件的可靠度了解不多,故采用理论模型预测的方法对先验系数进行求解,而其他组数据的先验估计是在前一组数据后验估计的基础上获得,根据上述结果对先验分布过程进行描述即可获得如图6所示等效后的Weibull过程先验等效概率密度分布图。然后根据先验分布参数及似然函数对过程参数的后验分布进行求解,进而得到如表6所示的Weibull过程参数的后验推断。运用后验参数对后验过程分布进行描述,即可得到如图7所示的概率密度分布图。
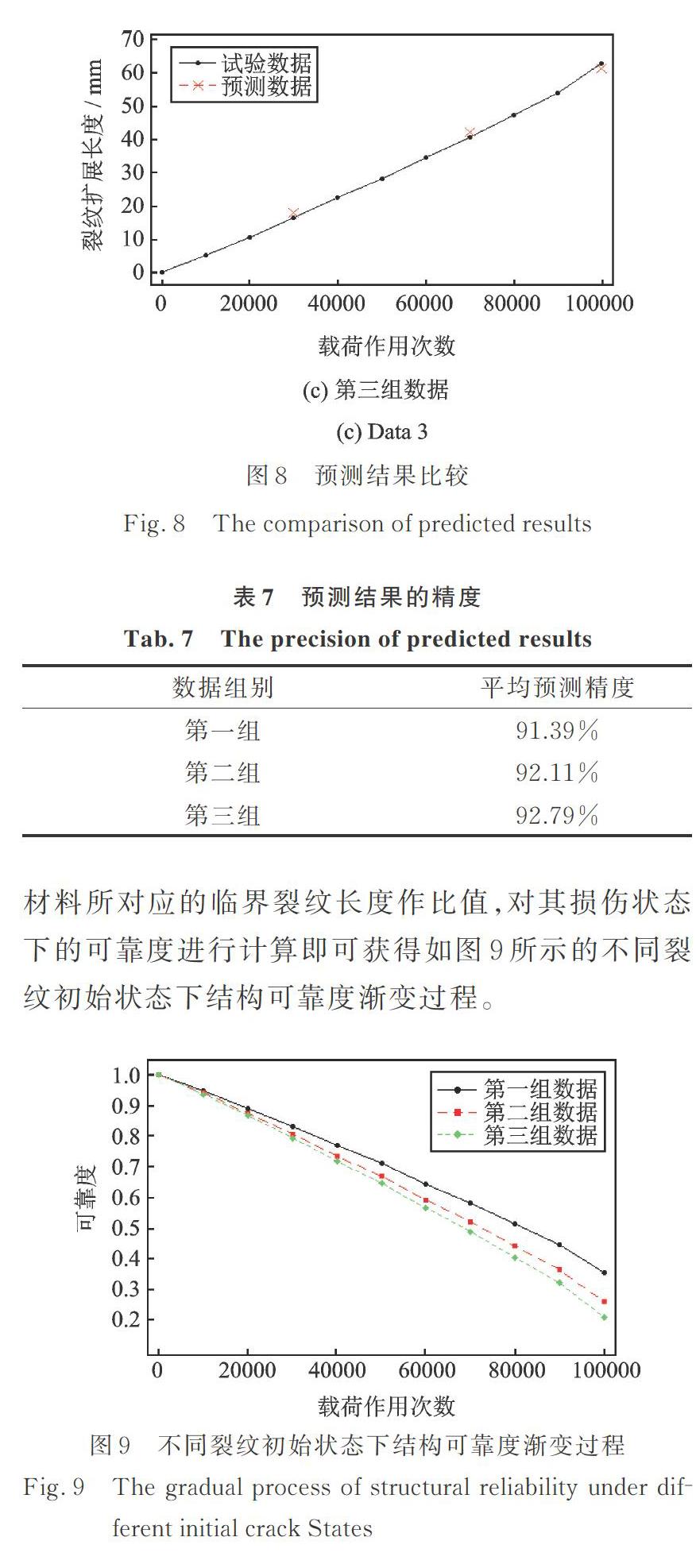
为了对孪生贝叶斯理论非齐次泊松过程的结构损伤评估方法的预测精度进行分析,分别将试验数据与后验模型的预测结果进行对比,即可获得如图8所示的结果。同时,根据测试数据与试验数据计算每个固定载荷作用次数所对应的预测精度,对每一组数据中3个固定载荷作用次数下的预测精度求平均值可以得到如表7所示的数据,统计后分析得到三组数据的平均预测精度为92.1%。
将如图8所示的预测数据中的裂纹扩展长度与材料所对应的临界裂纹长度作比值,对其损伤状态下的可靠度进行计算即可获得如图9所示的不同裂纹初始状态下结构可靠度渐变过程。
5 结 论
本文研究了一种孪生贝叶斯理论非齐次泊松过程的结构损伤评估方法,得出结论如下:
(1)基于可靠度序化策略与NHPP,获得了不同初始损伤状态下过程参数先验分布。同时,基于裂尖场能量递进因子与似然函数的概念,通过先验理论信息与试验信息复用的策略,建立了孪生贝叶斯理论NHPP的参数后验分布模型。
(2)运用孪生贝叶斯理论非齐次泊松过程的结构损伤评估方法对不同初始状态下典型结构的损伤评估进行了实例研究,研究结果表明测试数据的平均预测精度为92.1%,可以较好地实现通过少量现场试验信息完成不同初始损伤状态下构件可靠度评估的目的。
参考文献:
[1] 朱 林,賈民平,冯月贵,等. 考虑残余应力重分布情况下的裂纹扩展预测研究[J]. 机械工程学报, 2017, 53(8): 43-49.
Zhu Lin, Jia Minping, Feng Yuegui, et al. Prediction study of the crack propagation with consideration of the residual stress redistribution[J]. Journal of Mechanical Engineering, 2017, 53(8): 43-49.
[2] 朱 林,贾民平,林明智,等. 融合应力集中因子与贝叶斯理论的结构健康评估方法[J].机械工程学报, 2019, 55(24): 21-27+36.
Zhu Lin, Jia Minping, Lin Mingzhi, et al. Health assessment approach for structure by fusion of stress concentration factor and Bayesian theory[J]. Journal of Mechanical Engineering, 2019, 55(24): 21-27+36.
[3] Torregosa R F, Hu W. Probabilistic risk analysis of fracture of aircraft structures using a Bayesian approach to update the distribution of the equivalent initial flaw sizes[J]. Fatigue & Fracture of Engineering Materials & Structures, 2013, 36(11): 1092-1101.
[4] Beck J L, Au S K. Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation[J]. Journal of Engineering Mechanics, 2002, 128(4): 380-391.
[5] Luque J , Straub D . Reliability analysis and updating of deteriorating systems with dynamic Bayesian networks[J]. Structural Safety, 2016, 62: 34-46.
[6] 赵申坤,姜 潮,龙湘云.一种基于数据驱动和贝叶斯理论的机械系统剩余寿命预测方法[J].机械工程学报, 2018, 54(12): 115-124.
Zhao Shenkun, Jiang Chao, Long Xiangyun. A residual life prediction method of mechanical system based on data driven and Bayesian theory[J]. Journal of Mechanical Engineering, 2018, 54(12): 115-124.
[7] Zhu L, Jia M P. Estimation study of structure crack propagation under random load based on multiple factors correction[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2017, 39: 681-693.
[8] Peng W, Huang H Z, Li Y, et al. Life cycle reliability assessment of new products—A Bayesian model updating approach[J]. Reliability Engineering & System Safety, 2013, 112: 109-119.
[9] Miesowicz K, Staszewski W J, Korbiel T. Analysis of Barkhausen noise using wavelet-based fractal signal processing for fatigue crack detection[J]. International Journal of Fatigue, 2016, 83: 109-116.
[10] Gholizadeh S, Leman Z, Baharudin B. A review of the application of acoustic emission technique in engineering[J]. Structural Engineering and Mechanics, 2015, 54(6): 1075.
Abstract: A damage assessment approach for structure by twin Bayesian theory for non-homogeneous Poisson process is proposed, in which the damage for structure in the crack propagation is selected as the object. The prior parameter distribution for different damage situation is obtained by combine the reliability sequencing strategy based on crack tip field energy with the non-homogeneous Poisson model, and having an effective integration on the test information with the gradual relation by using Bayesian method. At the same time, the posterior distribution calculation approach based on Bayesian is achieved by using the prior information, based on the progressive factor of crack tip field energy and the likelihood function. Furthermore, the typical structure is selected as a case study. The evaluation results are compared with the test results. It can be clearly found from the results that the average accuracy of the proposed approach is 92.1%, and this approach can be used to complete the purpose of damage assessment by using a small amount of test information.
Key words: damage assessment; progressive factor; non-homogeneous Poisson; progressive strategy; Bayesian
作者簡介: 朱 林(1989?),男,讲师。电话:(0514)87978347;E-mail:zhulin157@163.com

