中学生物理成绩与其它多门学科的相关性研究


摘 要:中学阶段在人的求学一生中具有承上启下的重要作用,而物理学科具有重要的基础地位.所以有必要专门研究中学生物理学习成绩与其它多门功课之间的相关性问题.通过对中学生各个学科的成绩进行对比,采用SPSS23软件处理数据得到偏相关系数,定量得出物理与数学、化学相关程度较高,与语文关联程度很低,与英语、生物相关程度相对中等的结论.
关键词:中学生;物理成绩;相关性;偏相关系数;学习迁移
中图分类号:G633.7 文献标识码:B 文章编号:1008-4134(2021)01-0007-04
作者简介:朱俊林(1988-),男,安徽阜南人,硕士,助教,研究方向:大学物理教学及物理教育研究.
1 问题的提出
知识原本并无学科之分,随着生产力的发展和人类文明的进步,分工越发的精细.而知识的分类也越来越规范,由此诞生了学科.中学在人的求学一生中具有承上启下的重要作用,同时物理学科具有重要的基础地位.学习物理能够启发学生探索自然好奇心,同时也能为学生今后的深造打下基础.所以我们有必要专门研究影响中学生物理学习成绩的诸多因素.不可否认个体的认知差异以及生活经历对学习物理有着重要的影响,本文着重探索的是中学生物理成绩与其它诸多门功课之间的规律.
作为教师经常能听到一些说法,能学好数学的学生也能学好物理,能学好物理的学生脑瓜聪明等类似的话.这是教师的日常教育经验,属于教育认识的习俗形式.教育习俗性认识及由此产生的日常教育经验通常会有局限性,浮于表面.能不能经得起考验,必须用科学的方法来检验.
2 已有研究综述
现成的许多类似研究,大多是某两门功课之间的对比.例如,高中生数学对物理成绩影响的量化研究[1],中学阶段各学科相关系数差异分析及教学建议[2]等.大多数的研究者做相关性分析时,样本采集几乎都是割裂出要分析的两组数据做皮尔逊相关系数计算.
相关系数常用来反映变量之间的密切程度,问题是如果把其它的科目全都忽略而单独拿两门功课来研究它们之间的关系,得出的结论很可能是片面的.因为中学生要学的功课不止一门,在校期间学习时间总量是一定的,如果是单独用两个学科成绩做相关性比较的话,忽略了其它学科的影响也是不科学的.
基于以上考虑,除了把单独的两组变量列出做出一般性的散点图外,本文特别考虑到了高中理科所有的高考科目.列出六组变量运用控制变量法得出偏相关系数,因为充分考虑到了多变量影响,所以得出的结论更有说服力.
3 研究设计
3.1 研究目的及意义
本文选取某中部省份一所重点中学两千多名学生的六大学科成绩数据,旨在通过数据挖掘,量化分析高中生物理成绩与语文、数学、英语、化学、生物五大高考科目之间的相关性.
《國家中长期教育改革和发展规划纲要(2010-2020年)》指出全面提高普通高中学生综合素质,高中生要学习的文化科目中,语、数、英、物、化、生六科占据着极重要地位.通过本研究让更多的人认识不同学科之间的相关性和它们的特点,促进学生各学科的全面提高,提升高中生的综合素质.
同时也让更多的人认识学习迁移理论,服务于一线教师,把迁移理论用于学生培养,对于高中生的全面均衡发展具有重要意义.
3.2 样本选取
除去缺考人员设定三个样本:设定样本一,高一718人;样本二,高二709人;样本三,高三664人.样本选自不同的群体,不同学段,因此具有广泛的代表性.
3.3 数据处理工具
本次研究涉及一万两千多个数据处理,有六组变量而且数据之间可能存在复杂关系.因此借助SPSS Statistics23软件,利用了散点图功能和相关性分析功能.
3.4 研究方法及分析角度
首先,把不同样本的物理成绩与语文、数学、英语、化学、生物成绩单独列出来得到散点图,观察分布寻求规律.
其次,分别把样本一、样本二、样本三做偏相关性分析.偏相关性是指当两个变量同时与第三个变量相关时,将第三个变量的影响剔除.在实际情况中,相关分析往往有第三变量的影响,而使得相关系数不能真实地体现其线性相关程度.所以必须要用控制变量法,得出的结论才是更客观的.不考虑到这一点的话,难免会得出片面的结论.
最后,对相关性的量化指标做一个综合的对比得出结论.
4 研究结果与分析
4.1 物理与语文成绩的相关性分析
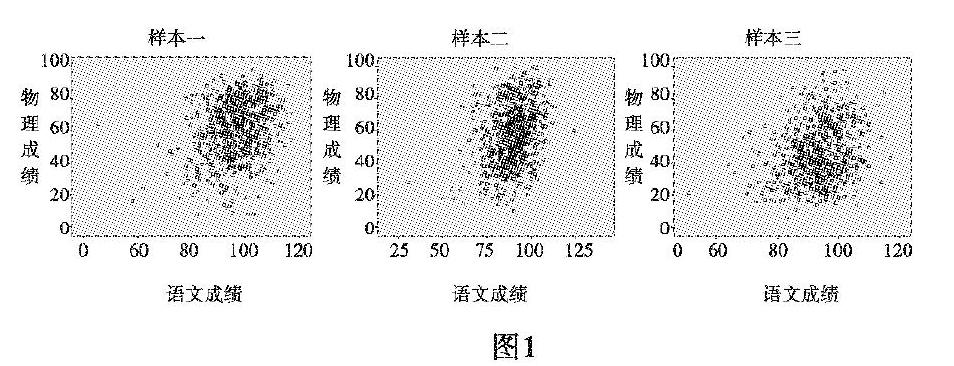
如图1分别是样本一、二、三物理成绩与语文成绩的散点分布图.即使是从高一到高三不同学段、不同群体,定性地看物理成绩与语文成绩正相关性不明显.
下面做进一步分析,对三个样本分别做偏相关性分析.由表1可见,样本一相关性0.051小于显著性(双尾)0.172,样本二0.027小于显著性(双尾)0.465,样本三相关性0.008明显处于低水平.由此得出结论:中学生的物理成绩与语文成绩相关性很小处于低水平.
4.2 物理与数学成绩的相关性分析
如图2分别是样本一、二、三物理成绩与数学成绩的散点分布图,呈现出明显的正相关性.
进一步分析由表2可见,样本一相关性0.306大于显著性(双尾)0.000,样本二0.289大于显著性(双尾)0.000,样本三相关性0.378大于显著性(双尾)0.000.由此得出结论:中学生物理成绩与数学成绩相关性明显而且处于较高水平.
4.3 物理与英语成绩的相关性分析
如图3分别是样本一、二、三物理成绩与英语成绩的散点分布图.与语文相比类似相关性不明显.
进一步分析由表3可见,样本一相关性0.170大于显著性(双尾)0.000,样本二0.098大于显著性(双尾)0.009,样本三相关性0.023小于显著性(双尾)0.555.我们发现物理与英语的相关性比较复杂,其相关性比语文高比数学小,相对处于中等水平.
4.4 物理与化学成绩的相关性分析
如图4分别是样本一、二、三物理成绩与化学成绩的散点分布图,呈现出明显的正相关性.
进一步分析由表4可见,样本一相关性0.361大于显著性(双尾)0.000,样本二0.386大于显著性(双尾)0.000,样本三相关性0.316大于显著性(双尾)0.000.由此得出结论:中学生物理成绩与化学成绩相关性明显而且处于较高水平.
4.5 物理与生物成绩的相关性分析
如图5分别是样本一、二、三物理成绩与生物成绩的散点分布图.与生物相比呈现出正相关性,相关性没有数学、化学明显却又比语文、英语明显.
进一步定量分析,由表5可见,样本一相关性0.226大于显著性(双尾)0.000,样本二0.185大于显著性(双尾)0.000,样本三相关性0.220大于显著性(双尾)0.000.由此得出结论:中学生物理成绩与生物成绩相关性处于较高水平.
4.6 结论
通过对比分析,物理与其它五门学科的相关性P物数>P物化>P物生>P物英>P物语.同时也能明显地看出物理与数学、化学的相关性处于相对较高的位置,物理与语文处于一个相对偏低的位置.
如何理解这种现象呢,从学科内容上来看,高中数学需要学生具备分析计算能力、逻辑推理能力和空间想象能力等.高中化学需要学生具备必要的计算能力和很强的逻辑推理能力.而高中物理也是需要很强的计算能力和空间想象能力,逻辑推理能力尤为重要.学习迁移是指人在一种情境中的学习影响他在其它情境中的学习.桑代克的共同要素认为,学习迁移就是相同联结的迁移,在两种学习中存在着共同的联结,一种学习上的进步转移到另一种学习上去.物理与数学、化学的正迁移效果明显.
语文、英语是语言类学科,在内容上它们和理科的物理差异性很大.但语言类学科的学习对记、用、模仿的相关能力要求很高.虽然它们与物理的相关性不那么明显,但是也存在一定的相关性.形式训练说认为,学习的迁移就是非物质的心灵功能受到发展的结果.即通过某种学习,使某种心灵功能得到训练,从而转移到其它学习上去.以这种观点来看,也能解释物理与语文、英语的某种相关性,只是在此处不占主导作用.
生物是一个文理掺半的学科,一方面对学生的逻辑推理、计算能力有一定要求,另一方面有众多需要记的概念和名词.它与物理的相关性综合了数学和语文与物理的相关性.这样就不难理解相关性P物数>P物化>P物生>P物英>P物语这样的现象了.
5 结束语
就物理与其它五门学科的相关性P物数>P物化>P物生>P物英>P物语结论和它们量化的指标而言,本文虽然是以考试分数为载体来进行研究,但也应客观地认识到,考试分数受多方面影响,仅仅依靠收集、整理、统计的一些数据还是不能够完全反映中学生的学习能力的.教育的天职是促进个体的发展,不能唯分数论.马克思主义教育学指出:既要看到教育现象的复杂性,不能用简单化的态度和方法来对待教育研究,又要坚信教育现象是有规律可循的.
本研究充分考虑到教育影响,教育影响即教育活动中教育者作用于学习者的全部信息.学生某一科的学习偏好很容易受科任教师的影响.例如,如果某个富有感染力的教师深受学生喜欢,课堂效果极好,学生平时也偏爱在这一科多花一些时间,样本数据过少和方法不当的话很容易得出偏差的结论.因此选取两千多个学生跨度不同、学段不同群体的上万个数据,应用到了控制变量法,从而有效避免了可能的偏差.例如,研究物理与语文相关性时用偏相关性显著性双尾是0.846,与不用控制变量法得到的结论有明显的不同.
一線教师如果能充分认识到不同学科的相关性以及背后的理论体系,就可以通过表层的现象分析出
背后的规律,从而用理论来指导教学实践,更好地培养学生铸造国之栋梁.
参考文献:
[1]赵阳.高中数学对物理成绩影响的量化研究[J].现代教育科学,2016(07):36-42.
[2]刘补云.中学阶段各学科相关系数差异分析及教学建议[J].考试研究,2016(05):67-73.
[3]王苑.高中理科生数学成绩与其它学科相关性分析[J].数学之友,2016(08):1-3.
(收稿日期:2020-10-27)

