基于重整化群理论的采空区群稳定性分析

李恩翀，张晨洁，赵中原

(1.会昌县融昌矿业有限公司， 江西 赣州市 342613；2.西北矿冶研究院， 甘肃 白银市 730900)

0 引言

地下金属矿山采用空场法开采时，会留下大量的空区和矿柱，矿柱是保证空区稳定不发生破坏的重要结构[1]。大量的研究表明，空区的稳定性与矿柱的稳定性紧密联系，大部分的地下矿山空区垮塌都是由于矿柱破坏引起的[2−4]。对于空区稳定性分析，国内外学者多采用数值模拟、现场调查分析、岩石力学经验公式计算等方法。杨宁等[5]采用3DMine-FLAC3D对复杂空区的稳定性进行了分析，并根据分析结果提出了相应的治理措施。宋卫东等[6]认为采空区群的稳定性分析是一个复杂的地质问题，在一定范围内具有群效应，对其分析必须掌握空区群的真实三维形态。彭欣等[7]采用ANSYS有限元模拟软件对广东大宝山矿特大采空区的稳定性进行了模拟分析，并分析了空区充填后采空区的应力状况，确保残留矿体的开采安全。重整化群起源于量子场论，卡丹诺夫和维尔森等将该理论应用与临界现象的研究，并取得巨大成功[8]。周子龙等[9]采用重整化群法对民窿空区群的级联失稳进行了分析评价。张淑坤等[10]采用重整化群理论对采用房柱法的采空区煤柱群的稳定性进行了研究，并给出了煤柱群的临界失稳概率范围。本文通过分析地下矿山空场法采矿空区群的赋存特征，建立了空区群一维重整化群分析模型，为地下矿山空区群稳定性分析及评价提供了新思路。

1 重整化群理论

1.1 一维重整化群模型

根据重整化群基本理论，首先建立采空区群稳定性演化重整化群一维分析模型。图1为建立的采空区群一维简化模型，在一维模型下，一个空区和相邻矿柱组成一个基本分析单元，两个基本分析单元组成一个一级原包。图2为一级原包中包含的两个矿柱所有的可能情况，其中（a）代表一级原包内的两个矿柱均发生破坏，（d）代表一级原包内的两个矿柱完整未发生破坏。

图1 采空区群一维重整化群模型

图2 一级原包内矿柱的所有可能情况

由图2可以得出，一级原包有4种发生可能，假定所有矿柱在开始发生破坏的概率均相当为p0，那么矿柱稳定不失稳的概率为1−p0。同时，考虑矿柱破坏必然会对周围矿柱的应力产生影响，导致其失稳概率上升，假设由于矿柱失稳破坏导致相邻矿柱发生破坏增加的概率相等且增加的概率为pab，pab计算公式为：

式中，Pa为矿柱未失稳破坏前相邻矿柱的破坏概率；Pb为矿柱失稳破坏后相邻矿柱的破坏概率。

若矿柱发生失稳破坏用u表示，不发生失稳破坏用b表示，根据概率论，一级原包共有4种发生情况，且每种情况发生失稳破坏的概率如下：

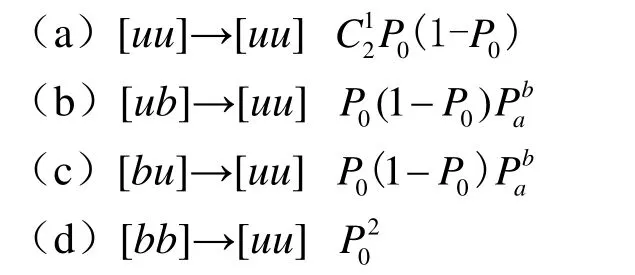
只有当一级原包内两个矿柱均发生失稳破坏，才认为一级原包发生破坏，那么，可得一级原包发生破坏失稳的概率为：

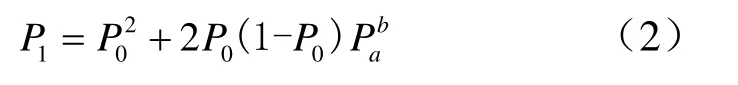
假设矿柱的失稳概率Pa服从Weibull分布规律，那么矿柱的失稳规律可表示为：

式中，σ为矿柱所承受的平均应力，MPa；σs为矿柱的极限承载强应力，MPa；m为拟合常数。

当公式（3）中的m=2时，矿柱的失稳概率p0=σ/σs，公式（3）可表示为：

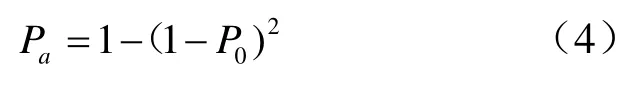
当一级原包内所有的矿柱发生失稳破坏才算一级原包破坏，矿柱破坏后会将应力传递到相邻矿柱，根据概率论，一级原包发生破坏的概率为：

根据logistic一维映射递推关系，可得到n级原包的破坏失稳概率为：

公式（6）即为一维状态下n级原包失稳概率，图3为Pn与Pn−1的映射关系曲线，从图3中可以看出，在[0, 1]的范围内，存在3个不动点，即当Pn−1=0，1，0.206时，Pn=Pn−1。

通过求解函数不动点得出空区群临界失稳概率为0.206。

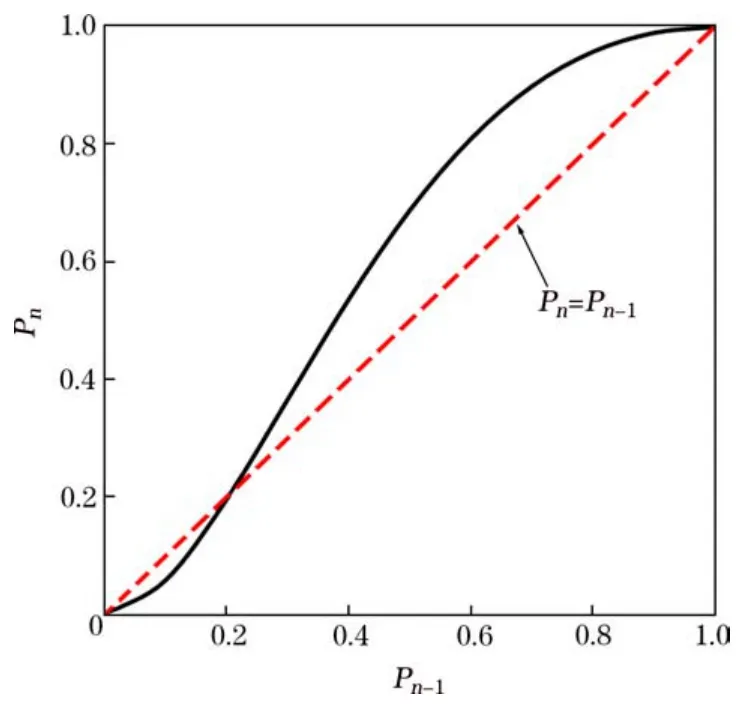
图3 Pn与Pn−1的映射关系

1.2 矿柱的失稳概率

矿柱失稳概率的计算方法比较多，本文采用矿柱横断面所受的平均应力与其极限承载强度之间的比值表示，其中矿柱横断面的平均应力计算公式如下：

矿柱的极限承载强度按式（8）计算：

矿柱的失稳概率按式（9）计算：

式中：σ为矿柱横断面所受的平均应力，MPa；σR为矿柱的极限承载强度，MPa；σc为岩石单轴抗压强度，MPa；Vc、Vm为岩石和岩体的纵波波速，m/s；ρ为岩石密度，kg/m3；H为上覆岩层的厚度，m；a、b、c、h分别为空区跨度、矿柱长度、矿柱宽度、矿柱高度。

2 工程应用

2.1 工程概况

白山泉铁矿于2006年建成投产，生产能力为110万t/a，采用分区开采方式，目前，一中段采矿已经结束，二中段已经开始回采。一中段采矿方法为分段凿岩阶段空场法，采场沿矿体走向布置，中段高度为40m，采场宽度为矿体厚度，设计间柱宽度为7.5m。一中段共分为2个采区进行回采，其中36～38线为一采区，56～60线为二采区。一采区采矿结束后形成由5个矿柱和5个空区组成的空区群，为了便于分析，命名为空区群I；二采区采矿结束后形成由9个矿柱和9个空区组成的空区群，命名为空区群II。空区群I和空区群II的赋存状态如图4和图5所示。

图4 空区群I的赋存状态

图5 空区群II的赋存状态

2.2 空区稳定性分析

根据采空区群一维重整化群模型，首先计算单个矿柱的失稳概率。通过现场实测空区I与空区II内所有空区与矿柱的形态参数，并对照一中段平面图，对各矿柱和空区的形态参数取平均值，计算得空区群I与空区群II的平均形态参数见表1，表2为空区群的岩石力学参数。

将表1中的数据带入式（8）中，计算得出空区群I和空区群II的矿柱平均应力为5.53 MPa和5.97 MPa，将表2中的数据带入式（9）中，计算得出空区群I和空区群II矿柱的极限承载强度为33.92 MPa和30.67 MPa。将计算结果带入式（10），可得空区群I和空区群II的矿柱失稳概率为0.162和0.195。根据采空区群一维重整化群模型，当空区群矿柱的失稳概率大于临界概率0.206时，空区群系统处于不稳定状态，空区群I和空区群II的矿柱失稳概率为0.162和0.195，均小于极限概率0.206，可得出空区群I与空区群II处于稳定状态，这与现场情况一致。一采区和二采区各空区均未发生垮塌事件，但从计算结果可以看出，空区群II的矿柱失稳概率为0.195，接近极限概率0.206，因此，对空区群II应加强监测，及时处理采空区。

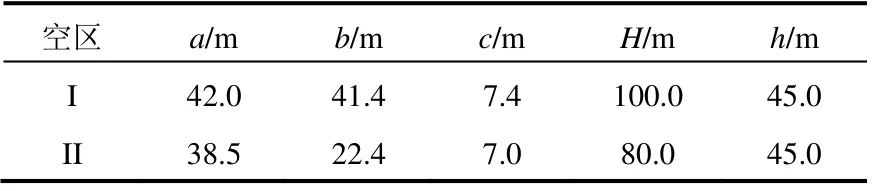
表1 空区群平均形态参数统计

表2 空区群岩石力学参数

2.3 数值模拟

为了进一步分析一中段一采区和二采区空区群的稳定性，并验证空区群一维重整化群模型的分析结果，采用ANSYS建立空区群模型，然后导入FLAC3D软件进行模拟计算，模拟采用的岩石力学参数见表3。

表3 数值模拟岩石力学参数

图6和图7为空区群I的位移分布云图和最大主应力分布云图。从图6可以看出，空区群I的位移等值线图呈拱形分布，最大竖向位移位于空区顶部区域，最大竖向位移为0.272 cm。从图7可以看出，空区顶部出现了拉应力区，最大拉应力值为0.324 MPa，小于岩石的抗拉强度，因此，空区群I较为稳定，不会发生整体失稳现象。图8和图9为空区群II的位移分布云图和剪应变增量云图，从图8可以看出，空区群II的最大位移位于矿房顶板区域，最大位移为0.381 cm。从图9可以看出，空区群II的顶板出现剪应变增量的拱形贯通区域，其剪应变增量值也相对较大，可能会发生采空区拱形冒落。

数值模拟结果与一维重整化群模型分析结果基本一致，都表明空区群II可能存在垮塌风险，应加强监测，及时处理采空区。

图6 空区群I位移分布云图（z方向）

图7 空区群I最大主应力分布云图

图8 空区群II位移分布云图（z方向）

图9 空区群II剪应变增量云图

3 结论

（1）以重整化群理论为基础建立了空区群一维分析模型，并考虑应力重分布对矿柱失稳概率的影响，根据概率论，推导了一级原包发生破坏的概率公式，并根据logistic一维映射递推关系，得到了n级原包的失稳概率函数，通过求解函数不动点，得出了空区群临界失稳概率为0.206。

（2）将建立的空区群一维重整化群模型应用于白山泉铁矿一中段2个采区的空区群稳定性分析中，分析结果表明，空区群I和空区群II的矿柱失稳概率为0.162和0.195，均小于临界失稳概率0.206，说明空区群处于稳定状态。空区群II的矿柱失稳概率0.195接近于临界失稳概率，应加强对空区群II的监测。

（3）为了验证空区群一维重整化群模型的分析结果，采用FLAC3D对空区群的稳定性进行了数值模拟分析。空区群I的位移分布和最大主应力均较小，空区群处于稳定状态。模拟结果显示空区群II的顶板出现了剪应变增量的拱形贯通区域，存在垮塌风险。数值模拟分析结果与空区群一维重整化群模型的分析结果基本一致，本文为空区稳定性分析提供了新思路。