“熟悉的陌生人”：巧作垂直妙解题

文 沈 莉

每年的中考题花样繁多，抽丝剥茧、仔细研究后，我们可以发现，有一些问题不过是“最熟悉的陌生人”，它们的基本模型是一样的，解决方式也是一样的。下面以2019年的一道中考题为例，一起来揭开这层面纱。

例1（2019·山东枣庄）在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D。如图1，点E、F分别在AB、AC上，且∠EDF=90°，求证：BE=AF。

图1

【分析】本题当然可以利用等腰直角三角形的图形特点，通过AD=BD，∠B=∠DAC，∠BDE=∠ADF，证 出△BDE≌△ADF，最终得到BE=AF。

如果对教材比较熟悉的话，我们就会想起另一种证法。苏科版数学教材八年级上册第59页第11题，是一个实验操作题：画∠AOB=90°，并画∠AOB的平分线OC。

（1）将三角尺的直角顶点落在射线OC的任意一点P上，使三角尺的两条直角边与∠AOB的两边OA、OB分别交于点E、F（如图2）。度量PE、PF的长度，那么这两条线段相等吗？

（2）将三角尺绕着点P旋转（如图3），PE与PF相等吗？

图2

图3

图4

图5

【分析】通过第一问的铺垫和角平分线的引导，很自然地想到过点P作PM⊥OA，PN⊥OB，垂足为M、N（如图4），所以∠PME=∠PNF=90°，∠MPE=∠FPN，再利用角平分线定理可得PM=PN，证得△PEM≌△PFN，即可得出结论PE=PF。

【方法归纳】在整个三角尺的旋转变化过程中，积极寻找其中的不变量：正方形PMON。利用其边PM始终与PN相等，构造出Rt△PEM和Rt△PFN，利用全等解决问题。

因此，回到2019年山东省枣庄市的中考题，我们便可以利用教材上的方法：如图5，过点D作DG⊥AB，DH⊥AC，通过证明△DGE≌△DHF，即可得出结论DE=DF，BE=AF。

此类问题都是利用了等腰直角三角形的性质，因此，我们可以将背景进行变化。

【变式1】如图6，正方形ABCD的对角线AC、BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合，将正方形A′B′C′D′绕点A′旋转，在这个过程中，OE等于OF吗？

图6

图7

【分析】我们同样只要过点O作OG⊥BC，OH⊥DC，如图7。通过证明△OGE≌△OHF，就能得到OE=OF。

【变式2】如图8，在矩形ABCD中，AB=6，BC=8，对角线AC与BD相交于点O，将三角尺的直角顶点落在O点，使三角尺的两条直角边与BC交于点E，与DC交于点F，求OE与OF的比值。

图8

图9

【变式3】如图10，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，将三角尺的直角顶点落在P点，使三角尺的两条直角边与AB交于点E，与BC交于点F，当AP=2PC时，求PE与PF的比值。

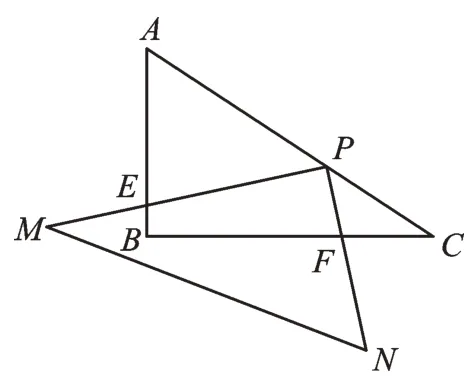
图10

【分析】可以通过一样的处理方式去添加辅助线，得到比值为