“相等”与“垂直”，紧紧两相依

文 郑小娇

正方形是特殊的平行四边形，通过它特殊的性质，我们可以发现很多有趣的结论。

【基本问题1】如图1，在正方形ABCD中，若点E、F分别在BC、CD上，且AE⊥BF，垂足为M，那么AE与BF相等吗？

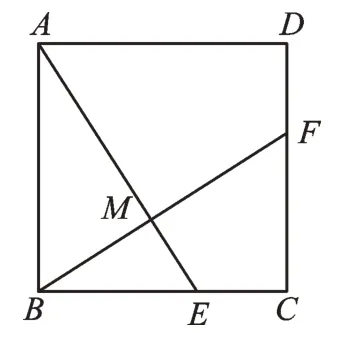
图1

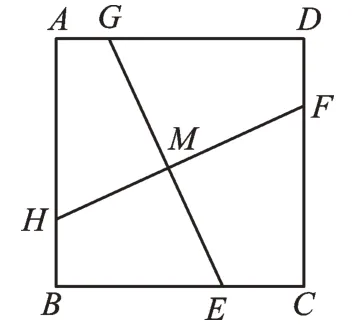
图2

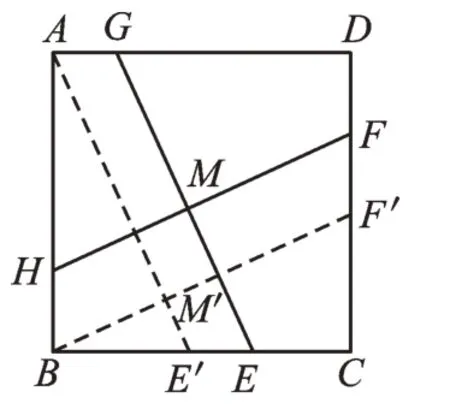
图3

【分析】由正方形ABCD，得AB=BC，∠ABC=∠C=90°，∴∠BAE+∠AEB=90°。∵AE⊥BF，∴∠FBE＋∠AEB=90°，∴∠FBE=∠BAE，∴△ABE≌△BCF，∴AE=BF。

【变式】如图2，在正方形ABCD中，若点E、F、G、H分别在BC、CD、DA、AB上，且GE⊥HF，垂足为M，那么GE与HF相等吗？

【分析】过点A作GE的平行线交BC于点E′，过点B作HF的平行线交CD于点F′，如图3，则问题转化为【基本问题1】。

【基本问题2】如图1，在正方形ABCD中，若点E、F分别在BC、CD上，且AE=BF，那么AE⊥BF吗？

【分析】由正方形ABCD，得AB=BC。又AE=BF，∠ABC=∠C=90°，∴Rt△ABE≌Rt△BCF。∴∠BAE=∠FBC，∴∠FBC+∠AEB=90°，∴AE⊥BF。

【变式】如图2，在正方形ABCD中，若点E、F、G、H分别在BC、CD、DA、AB上，且HF=GE（AG＜BE，DF＜AH），那么HF⊥GE吗？

【分析】过点A作GE的平行线交BC于点E′，过点B作HF的平行线交CD于点F′，则问题转化为【基本问题2】。

【总结】如图1，在正方形ABCD中，由AE=BF可 得AE⊥BF，由AE⊥BF可得AE=BF。由此，在解决其他问题时，就可以将“AE=BF”与“AE⊥BF”通过△ABE≌△BCF联系起来，由此为突破口，从而找到解决问题的方法。若将“AE=BF”替换成“BE=CF”，“BE=CF”与“AE⊥BF”亦可通过△ABE≌△BCF联系起来。

下面我们运用这两个基本原理解决相应的问题。

【运用1】如图4，已知正方形ABCD的边长为4，点E、F分别在BC、CD上，AE=BF，AE与BF相交于点M。

（1）若AE=5，点H为AF的中点，连接MH，则MH的长为________。

（2）当点E在BC边上运动时，CM的最小值为 。

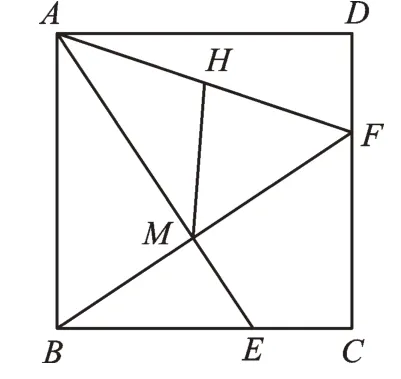
图4

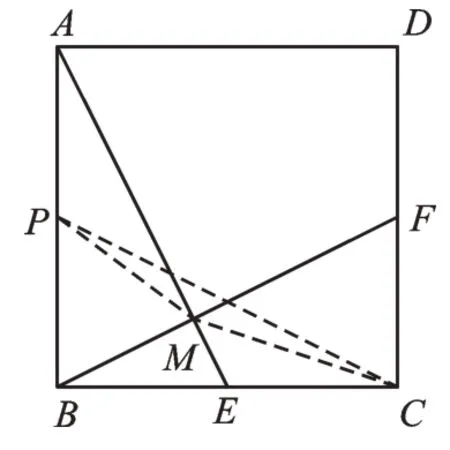
图5

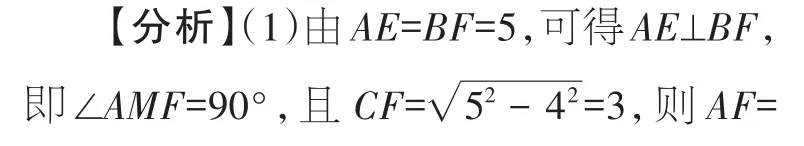
【运用2】如图6，在正方形ABCD中，若点E、F分别在BC、CD上，且AE⊥BF。

（1）四边形ECFM与△ABM的面积相等吗？说明理由。

（2）若AB=5，阴影部分的面积与正方形的面积之比为4∶5，求△ABM的周长。

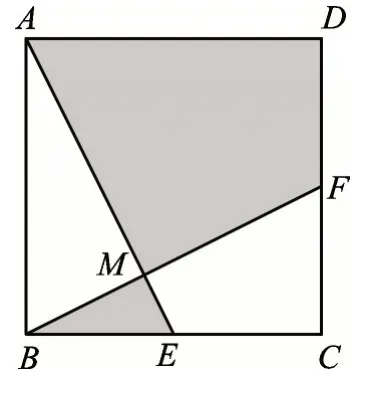
图6

【分析】（1）由【基本问题1】可得△ABE≌△BCF，则△ABE与△BCF面积相等，又∵S四边形ECFM=S△BCF-S△BME，S△ABM=S△ABES△BME，∴S四边形ECFM=S△ABM。