筒型永磁涡流阻尼特性理论建模及实验研究

汤劲松，刘 宁，杨博伦，孙明亮

（南京理工大学机械工程学院，江苏 南京 210094）

1 引言

电涡流原理广泛应用于测试[1]、制动等领域。电涡流阻尼器利用导体切割磁感线，在导体中产生电磁涡流，形成反向感应磁场并产生涡流阻尼力，阻碍原磁场与导体相对运动并消耗一部分动能。而传统液压阻尼器依靠机械摩擦耗能，需要工作流体，长期使用的阻尼器将不可避免地出现磨损和液体泄漏等现象，降低阻尼器使用寿命、增加维护成本。相比之下，电涡流阻尼器具有非接触、无摩擦，结构简单、可靠性高等优点，广泛应用于航空航天、建筑桥梁、高速列车和军事装备等减振制动领域。

文献[2-5]对板式电磁涡流阻尼器进行了试验和有限元分析，分析了导体板厚度，导磁钢板厚度等多种因素对阻尼器性能的影响规律。文献[6]对强冲击载荷下筒式永磁涡流阻尼器阻尼性能进行了研究，分析了强冲击载荷下阻尼器的阻力特性。文献[7]提出了一种新型的可用于航天器振动被动抑制的永磁涡流阻尼器，进行了三维瞬态磁场有限元分析和实验研究，验证了该结构的可行性。文献[8]研究了电涡流阻尼器在数控加工过程中的振动抑制作用。文献[9-11]研究了永磁涡流阻尼器对悬臂梁振动的抑制效果，分析了不同空气间隙下的阻尼比，并且比较了单个永磁体和两个永磁体对称分布两种不同情况下的结果。文献[12]研究了永磁体在圆柱导体筒中运动的规律，但在推导涡流阻尼系数时，为了简化计算将径向磁感应强度沿外筒径向分布近似为一常数，使得理论结果与实际情况相差较大。

筒形永磁涡流阻尼器已广泛应用于装备制动领域，但缺乏可靠实用的理论模型指导工程设计。基于电磁涡流理论，推导了永磁体在圆柱导体筒内阻尼运动理论模型，开展筒形永磁涡流阻尼实验研究，修正理论模型，并与有限元结果进行对比验证及分析。这将为深入研究工程实际中的复杂永磁涡流阻尼器的理论模型、力学性能等奠定基础。

2 筒型永磁涡流阻尼特性理论建模

2.1 圆柱形轴向充磁永磁体磁场分布

根据圆柱形永磁体磁场分布的对称性，建立空间直角坐标系，原点位于永磁体轴线中点，z 轴沿圆柱轴线，如图1 所示。

图1 圆柱形永磁体空间坐标系Fig.1 Cylindrical Permanent Magnet Coordinate System

对上式积分可得：

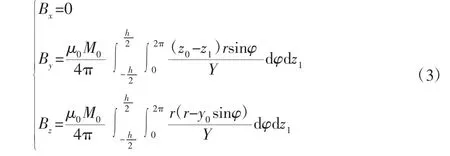
式中：Bv—径向磁感应强度；Bz—轴向磁感应强度，表达式为椭圆积分，采用数值积分方法进行计算。

2.2 永磁体在导体管中阻尼下落运动分析

永磁体在导体管中阻尼下落运动示意图，如图2 所示。

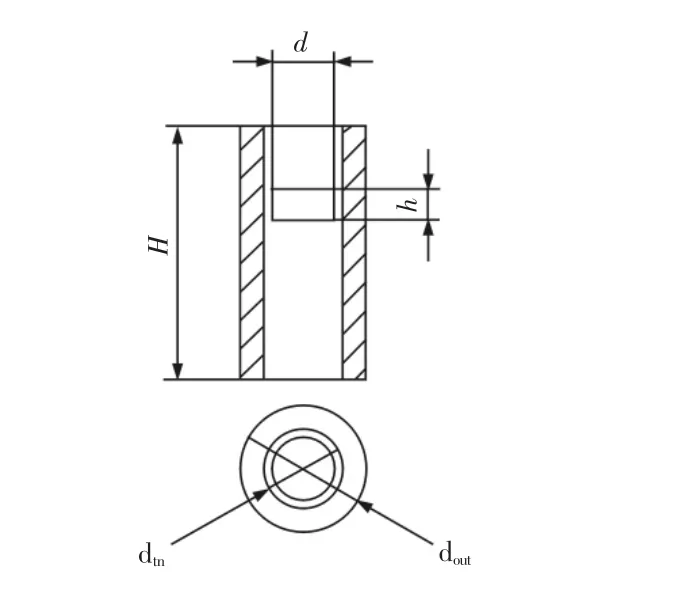
图2 永磁体在导体管中阻尼下落运动示意图Fig.2 Schematic Diagram of a Damped Falling Motion of a Permanent Magnet in a Conductor Tube

根据电磁场理论，永磁体在导体筒内运动所受的电磁力为：

式中：m—永磁体质量；g—重力加速度；Ff—运动过程中受到的阻力。

3 实验研究

3.1 速度公式修正

为了验证上述模型的正确性，设计了圆柱形永磁体在导体筒内阻尼下落实验系统，永磁体材料为NdFe35，直径D=20mm，轴向长度h=10mm，质量m=20.3g，磁化强度M=700000A/m。导体管材料为铜，内径，外径，轴向长度H=300mm，导电率σ=580000S/m。实验测量装置由ILD 1402-600SC 激光位移传感器、信号线、铜管、永磁体组成，实验器材示意图，如图3 所示。实验测量时，先通过释放工具使永磁体位于铜管内部且与铜管同轴，然后释放永磁体进行测量。

图3 实验测量装置示意图Fig.3 Schematic Diagram of Experimental Equipment

为了排除装置加工精度和永磁体释放过程对下落运动的影响，首先采用相同质量的圆柱形45#钢进行自由落体实验，测得钢块下落速度，如图4 所示。由实验结果可知，在物块下落一段时间后速度与时间基本呈线性关系，但是在下落的初始时间，由于实验装置、物块释放操作等因素，导致初始段内加速度由零逐渐增大然后才趋于恒定，存在一个初始过渡段。

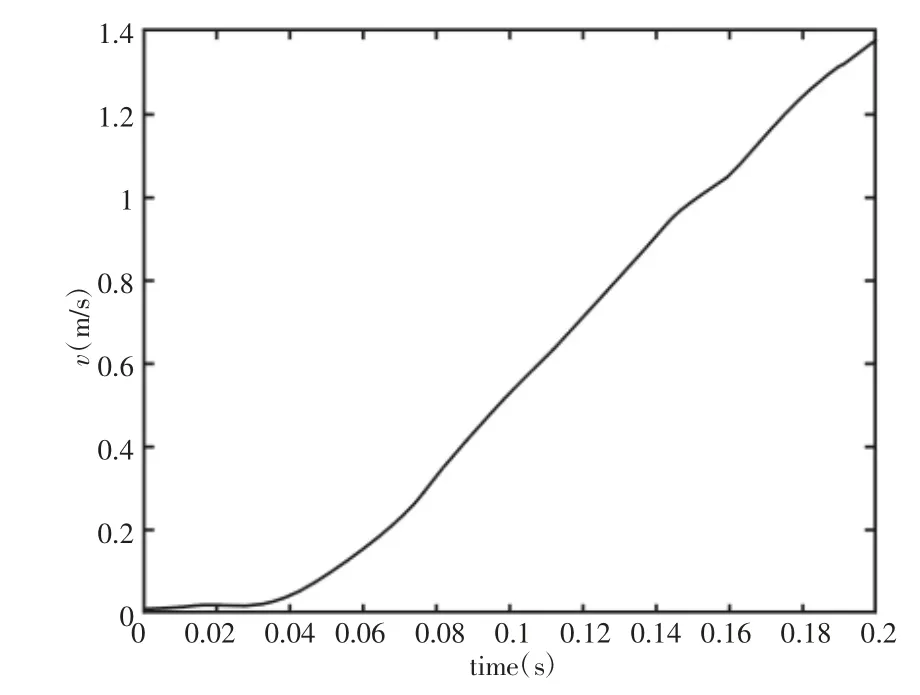
图4 物块自由下落速度随时间变化Fig.4 The Free Falling Velocity Curve of the Block

修正函数能够很好的反映出初始一段时间内速度的变化趋势。因此可用同样形式的修正函数对永磁体阻尼下落速度式（7）进行修正：

1967年，美国的CBS技术研究所发表开发电视录像商品的计划时第一次提出新媒体的概念，由此可以看出，新媒体的概念已经很早就出现了。当下，对于新媒体的概念众说纷纭，在这篇论文中将新媒体的概念定义为：新媒体概念是相对于传统媒体来说的，是随着新技术、新需求、新网络以及新信息发展起来的一种媒体形式，具体来说，就是将电视、报纸、广播以及杂志等分类为传统媒体，那么电脑以及智能手机等就可以归类为新媒体。

图5 钢块下落修正后的理论与实验曲线对比Fig.5 Theoretical After Correction and Experimental Curves of the Steel Block Free Fall

3.2 实验验证

由于永磁体质量过小，阻尼力增大到与重力平衡的时间很短。在永磁体上加恒定主动力，以延长其运动达到平衡状态的过程。实验测得永磁体位移随时间变化曲线，如图6 所示。其中，主动力4.12N，如图6（a）所示。主动力3.12N，如图6（b）所示。

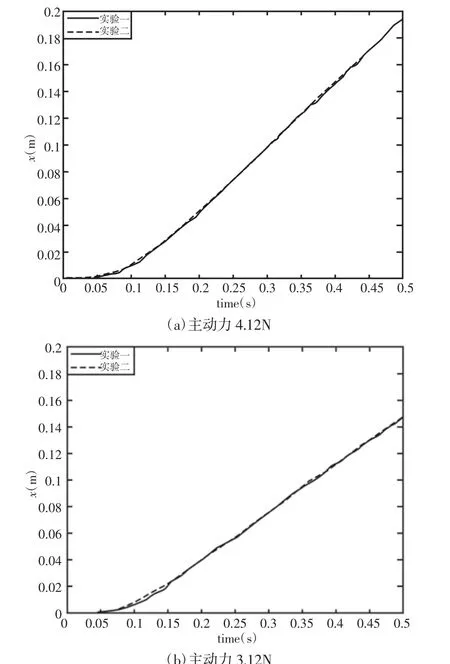
图6 实验测得位移随时间变化规律Fig.6 The Displacement is Measured with Time

永磁体运动过程中受到阻力0.8N，速度修正公式与实验测量得到的速度随时间变化曲线，如图7 所示。其中，主动力4.12N，如图7（a）所示。主动力3.12N，如图7（b）所示。

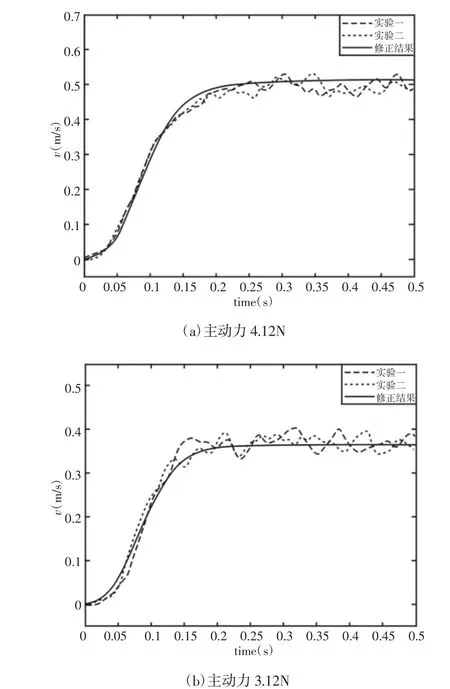
图7 永磁体阻尼下落速度修正公式与实验曲线对比Fig.7 Modified Formula and Experimental Measurement Velocity Curves for Permanent Magnet Damping Fall

当不考虑阻力和实验装置等因素影响时，永磁体阻尼下落的初始时刻速度为零，阻尼力也为零，因此初始时刻加速度大小即为重力加速度。随着速度增大，阻尼力也增大，永磁体做加速度减小的加速运动直到阻尼力大小等于重力，永磁体达到平衡状态。考虑实际情况时，由图7 中实验结果可知，同物块自由下落一样，永磁体下落也存在一个初始过渡段，但是最终永磁体达到匀速运动。主动力越大，稳定时速度越大，主动力为4.12N 时，稳定速度约为0.49m/s，主动力为3.12N 时，稳定速度约为0.34m/s。同时由图7 可知，修正后的计算结果与实验结果吻合，这验证了理论模型的正确性。

4 理论结果分析及讨论

为了便于分析，以下讨论均不考虑实验中的实际影响因素，即在理想情况下进行讨论，并用Maxwell 数值分析软件进行对比验证。

4.1 永磁体磁场分布

由阻尼系数表达式可知，阻尼系数的大小仅与阻尼装置结构及永磁体空间磁场分布有关。为了计算阻尼系数的大小、分析其影响因素，有必要先计算永磁体空间磁场分布。

平行于轴线距轴线10.5mm 处的一条线上的径向磁场分布，如图8（a）所示。永磁体与轴线重合的线上轴向磁场分布，如图8（b）所示。为了验证理论模型的正确性同时给出了Maxwell 软件有限元计算结果。两种方法计算得到的径向和轴向磁场分布吻合较好。

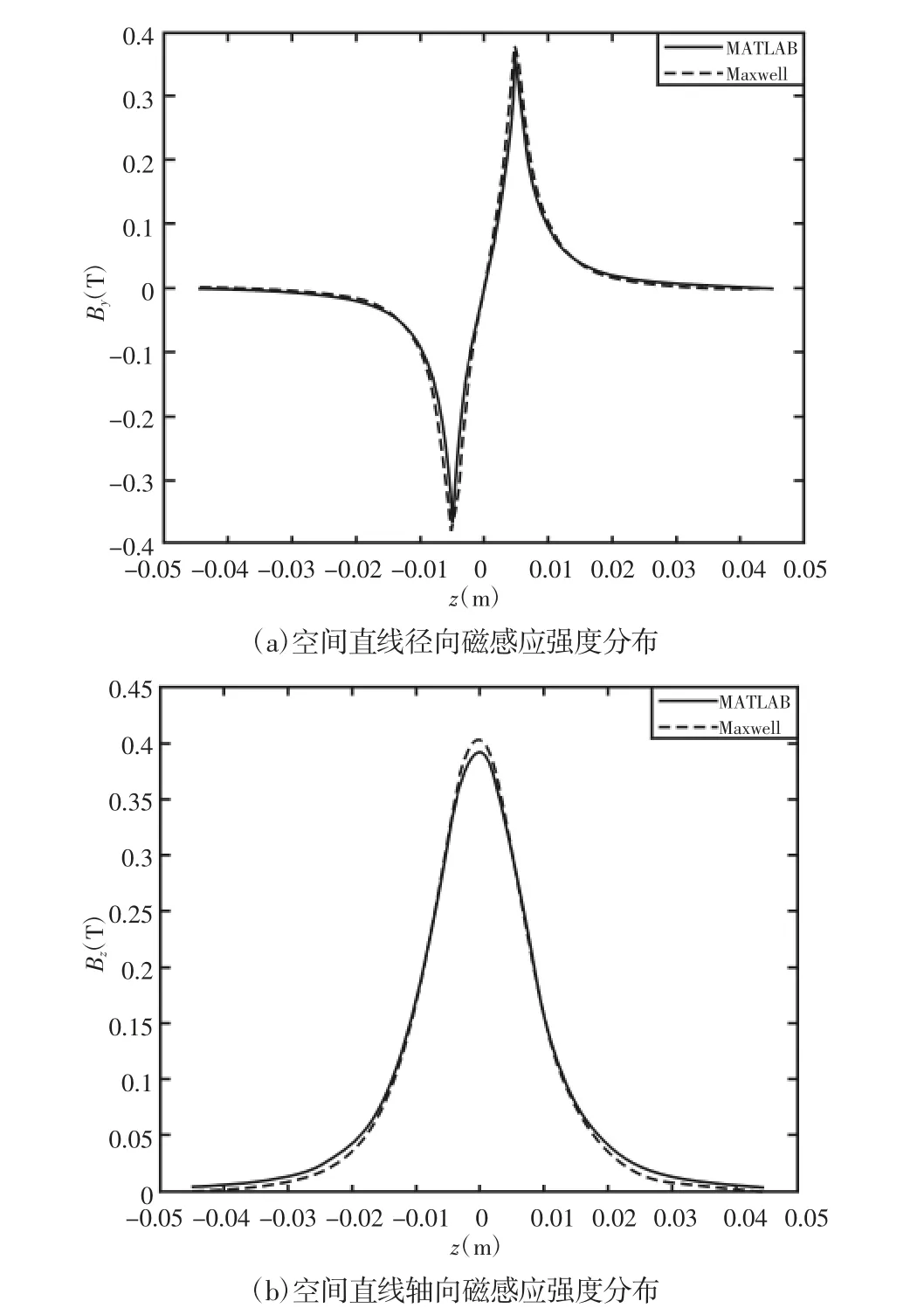
图8 磁场强度分布Fig.8 Magnetic Induction Intensity Distribution

永磁体上表面径向磁感应强度沿半径方向分布规律，如图9所示。由图可知，永磁体径向磁场沿半径方向变化较大。因此对于一般非薄壁筒，阻尼系数不能使用简化积分求解。

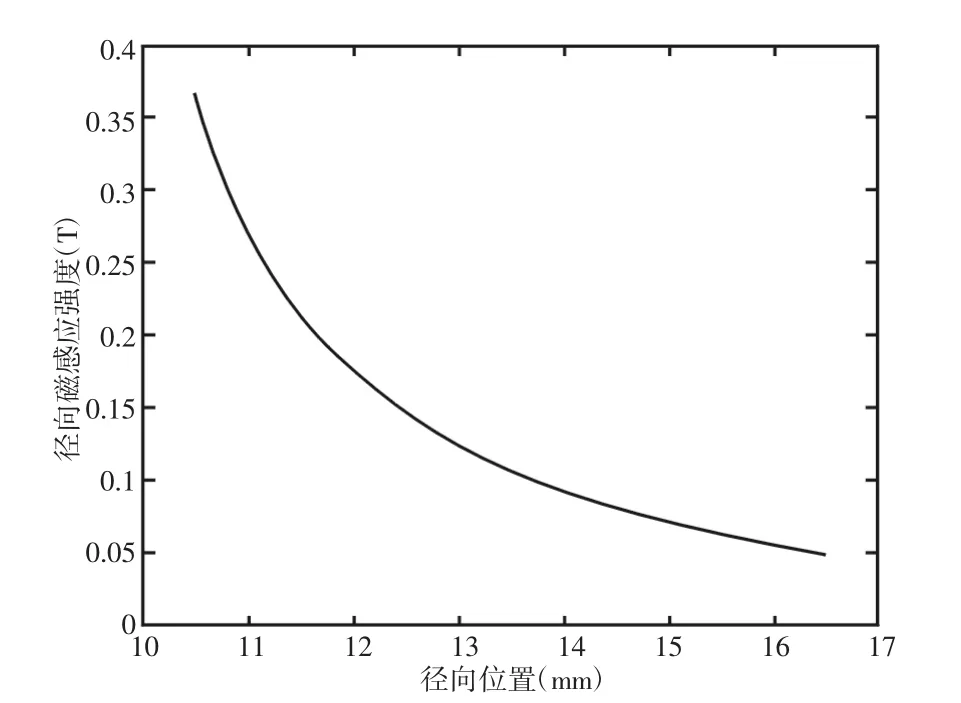
图9 永磁体磁感应强度沿半径方向变化规律Fig.9 The Magnetic Induction Intensity of Permanent Magnet Changes Along the Direction of Radius

4.2 阻尼系数及永磁体阻尼下落速度计算

由阻尼系数计算公式求得阻尼系数两重数值积分结果为6.7442N·s/m，简化积分结果为18.6372N·s/m。永磁体加配重后的质量为m=420.1g，两种积分及Maxwell 仿真求得的速度随时间变化规律，如图10 所示。由图可知两重积分理论计算和仿真分析的结果基本一致。但是由于永磁体磁感应强度随空间位置变化较大，因此简化积分求解结果误差较大。仿真分析得到的永磁体运动过程中的本构曲线，即阻尼力随速度变化的曲线，如图11 所示。由图11 可知，在永磁体的运动过程中，阻尼力与速度关系近似为线性，线性直线的斜率即为阻尼系数。由本构曲线计算得阻尼系数为6.8667N?s/m，与理论公式求解的结果基本一致。

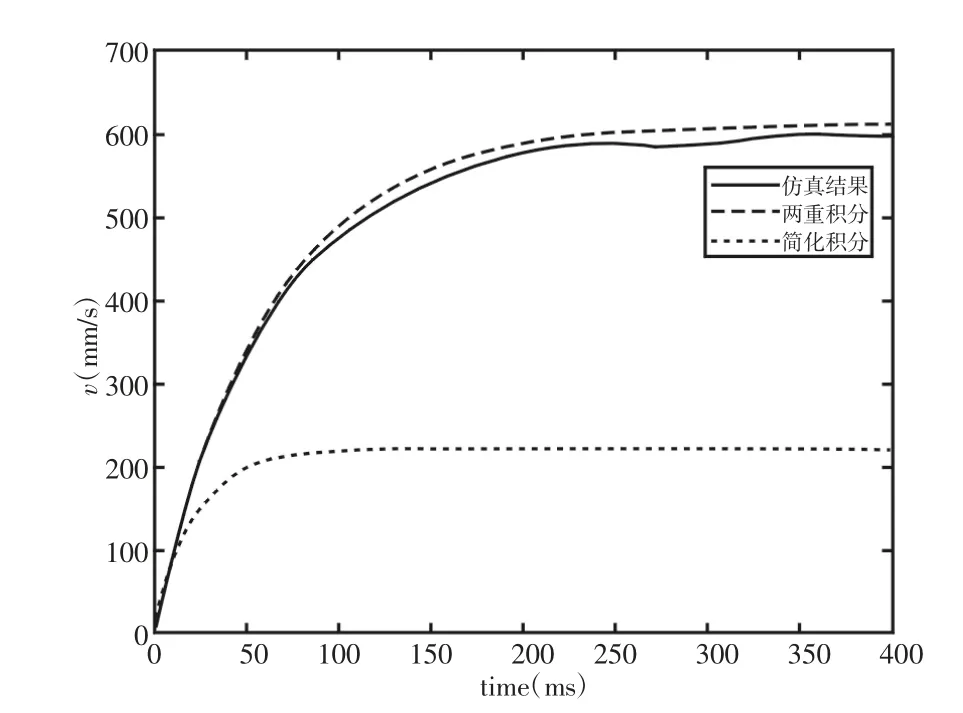
图10 速度随时间变化结果Fig.10 The Velocity Curves Over Time

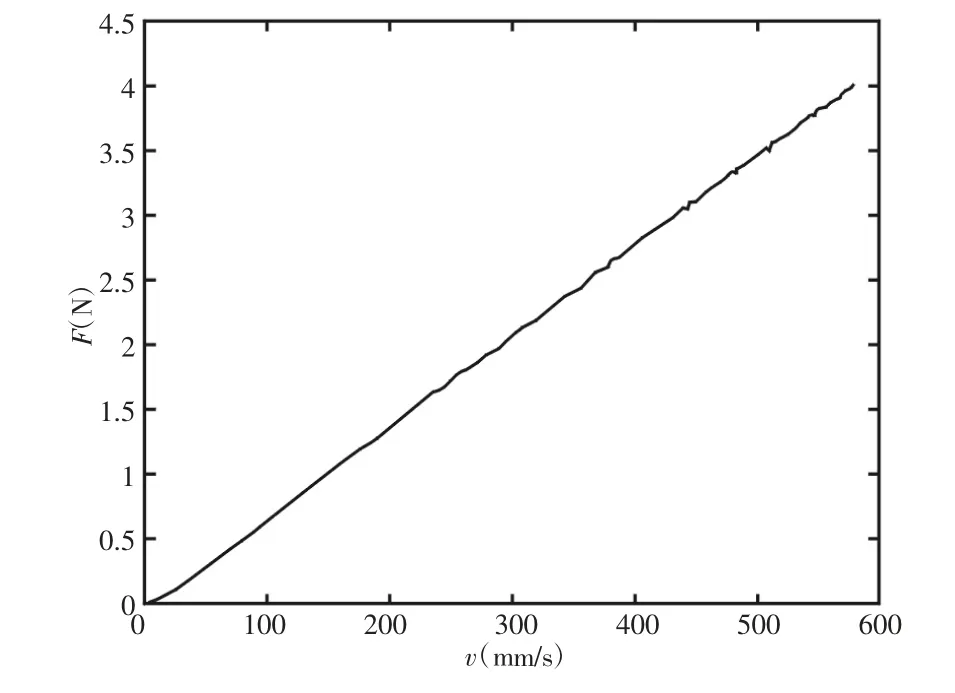
图11 永磁体运动过程本构曲线Fig.11 Constitutive Curve of Permanent Magnet Motion Process

4.3 涡流阻尼系数影响因素分析

由阻尼系数表达式可知，当永磁体在导体管中的相对位置变化时，积分区域H 也会发生相对变化。因此阻尼系数会随永磁体在导体管中的相对位置变化而变化，永磁体中间横截面相对于导体管底面的距离变化时阻尼系数的取值变化规律，如图12 所示。上图表明，当永磁体位于导体管内部距两端一定距离时，阻尼系数可视为一常数，这是永磁体磁场沿轴向分布所致。如图8（a）所示，永磁体径向磁场沿轴向迅速衰减。当永磁体距导体筒两端较近时，有一部分磁场未进入筒内，导致阻尼系数较小；当永磁体距两端一定距离时，未进入筒内的磁场较小可忽略不计。

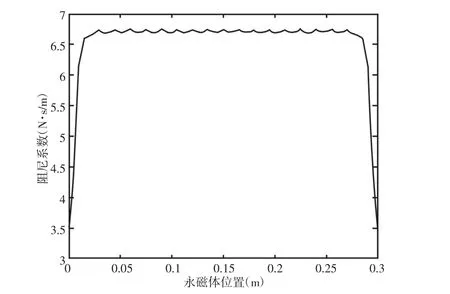
图12 阻尼系数随永磁体位置变化规律Fig.12 The Damping Coefficient Varies with the Position of Permanent Magnet

导体筒壁厚从1mm 到30mm 阻尼系数的计算值，如图13所示。由图可知，阻尼系数的大小随壁厚增大而增大，但是其增长趋势逐渐变缓。因此，可以通过增大壁厚的方式来增大阻尼系数，但是当壁厚达到一定大小后，阻尼系数随壁厚的增大趋势不明显。永磁体与导体筒不同间隙时的阻尼系数变化，如图14 所示。由图可知，阻尼系数的大小随间隙的增加迅速减小直至趋近于0。因此，理论上可以通过减小间隙的方式来增大阻尼系数。

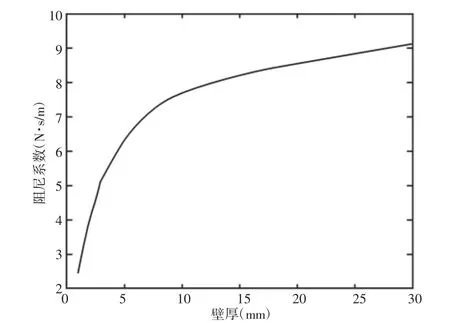
图13 不同导体筒壁厚下阻尼系数随导体筒厚度的变化规律Fig.13 The Damping Coefficient Varies with the Thickness of the Conductor Tube

图14 不同空气间隙下阻尼系数随间隙大小的变化规律Fig.14 The Damping Coefficient Varies with the Air Gap

以上均是由永磁体磁场沿径向分布所致。由图9 可知，永磁体磁场沿径向迅速衰减。当导体筒壁厚增大，参与被导体筒切割的磁感线增加，但是壁厚增大到一定程度后，磁感应强度较小，引起阻尼系数的增大不明显。当空气气隙增大时，靠近永磁体较强的一部分磁场未参与导体筒切割磁感线，因此阻尼系数迅速减小。

5 结论

对永磁体在导体筒中阻尼下落运动涡流阻尼特性进行了研究，推导了圆柱形永磁体磁场空间分布公式以及电磁涡流阻尼系数公式。结果表明：（1）在实际情况下，永磁体的运动规律与理想状态相差较大，主要在运动的初始存在一个过渡段。引入一个修正函数对永磁体阻尼下落速度理论公式进行修正，在永磁体加不同配重的情况下进行了两组实验，测得永磁体运动规律和修正后的理论公式吻合。（2）磁感应强度大小随空间位置分布变化较大，因此对于一般非薄壁筒，阻尼系数计算使用简化积分计算结果误差较大。（3）永磁体与导体筒的相对位置对阻尼系数影响较小，当永磁体在导体筒内部时，其阻尼系数可近似为一常数。导体筒的壁厚和永磁体与导体筒的间隙对电磁涡流阻尼系数均有显著的影响，这均是永磁体空间磁场分布所致。在一定范围内可以通过增大壁厚或者减小空气间隙的方式增大阻尼系数。但是超过一定的范围后，增大壁厚带来的效果不明显，而空气间隙过小将会使制造和装配困难。