机器人喷涂曲面涂层生长模型及均匀性分析

董慧芬，刘健健，高爽笑

（中国民航大学电子信息与自动化学院，天津300300）

1 引言

飞机执行飞行任务中，发动机叶片的燕尾基座受力磨损严重，需要定时进行润滑剂喷涂。喷涂效果是改善喷涂质量、提高性能的关键[1]。以航空发动机叶片燕尾基座为代表的曲面工件喷涂，主要采用传统手工喷涂方法，质量难以保证，无法满足喷涂均匀性的要求，机器人喷涂逐渐成为表面涂装的发展趋势[2]。目前对机器人喷涂的研究主要集中在喷枪运动轨迹的规划、优化等方面[3]。文献[4]提出了基于动态基准面的三角网格分块方法，为喷枪在块边界上的平稳运动提供支持，提高了边界处涂层的均匀性。文献[5]利用抛物线模型，将曲面进行分片处理，研究喷枪轨迹优化方法。文献[6]对喷枪变速喷涂的轨迹规划方法和速度优化方法进行了研究。喷枪数学模型的建立是喷涂理论中涉及的重要问题之一，准确的喷枪模型是喷涂涂层均匀性研究的基础[7]。目前应用广泛的喷涂数学模型有高斯分布模型[8]、柯西分布模型[9]、抛物线分布模型[10]和β 分布模型[11]等。喷涂厚度的均匀性是检验喷枪数学模型有效性的重要指标，同时也是优化机器人喷涂轨迹的基础。喷涂厚度的均匀性与喷涂工件宽度、喷涂初始行程、重叠宽度和终喷行程的关系非常复杂，其常用的评价目标函数包括厚度方差，归一化方差，平均绝对方差，平均相对偏差和最大偏差等。目前平面工件展开研究的较多，曲面工件喷涂均匀性的研究相对较少。对曲面喷涂的均匀性进行研究，采用与空气中喷涂涂层累积模型相似的抛物线模型，作为单点涂层生长模型，以涂层厚度平均相对偏差作为评价函数建立曲面工件喷涂数学模型，并进行仿真实验验证。

2 喷涂涂层累积抛物线模型

表征涂层厚度分布的抛物线模型和空气喷涂的实验结果比较相似，可以较为真实的反应涂层的分布情况，因此选择抛物线模型作为涂层厚度分布模型，直角坐标系下的模型表达式为：

式中：T（X）—任意一点的涂层厚度；Tmax—最大厚度；W—喷幅宽度；X—喷幅方向上以喷幅中心为原点的测量距离，-W/2≤X≤W/2。

为了便于计算，将公式进行无量纲处理，得到：

3 曲面涂层生长模型建立

对于复杂曲面，其面上的某些点具有曲率较大和复连通的特点，为了简化研究复杂曲面喷涂的复杂度，提高喷涂涂层均匀度，先研究简单的曲面（即曲率半径固定的曲面），选择抛物线模型为喷枪模型，进行曲面喷涂的均匀性研究。曲面涂层生长模型示意图，如图1 所示。

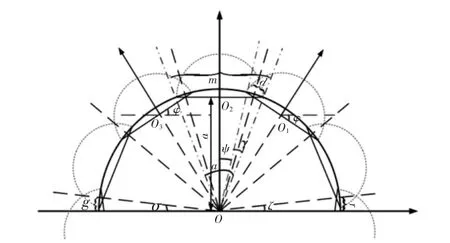
图1 曲面涂层生长模型示意图Fig.1 Curved Coating Growth Model

曲面涂层生长模型中，一条粗实线表示球形喷涂工件的横截面，另一条虚线表示喷枪模型在垂直行程方向的截面上单行程产生的喷涂厚度，每个喷涂行程以匀速且相同的重叠宽度进行喷涂，喷涂行程与横截面法线方向相同，如图1 所示。每个点的涂层厚度为各个行程喷涂累计的结果。模型中的参数解释，如表1 所示。

表1 曲面涂层生长模型参数解释Tab.1 Parameter Interpretation of Curved Coating Growth Model

在直角坐标系下，曲面工件的涂层厚度计算过于复杂，因此通过坐标变换，把每个行程的函数的坐标系转化到大圆弧的坐标系下，并在极坐标系下统一计算涂层厚度。

4 曲面喷涂均匀性评价函数建立

涂层的均匀性评价函数一般采用厚度方差、归一化方差、平均绝对方差、最大方差或者平均相对偏差表征。其中平均相对偏差相对于其他均匀性评价函数计算简单，能够直观反应整体涂层厚度的均匀程度，是实际生产最实用的涂层均匀性检验指标。因此，采用平均相对偏差表征评价指标，建立曲面喷涂涂层均匀性评价函数。

4.1 喷涂涂层平均厚度函数

平均喷涂厚度是计算平均相对偏差的基础，已知模型中工件的弧长为l，首先将模型的涂层累积函数进行分段，如图2 所示。设n（m-d）区间的涂层厚度之和为sn，n 为（l-g）/（m-d）的向负取整数值，sn可以表示为：

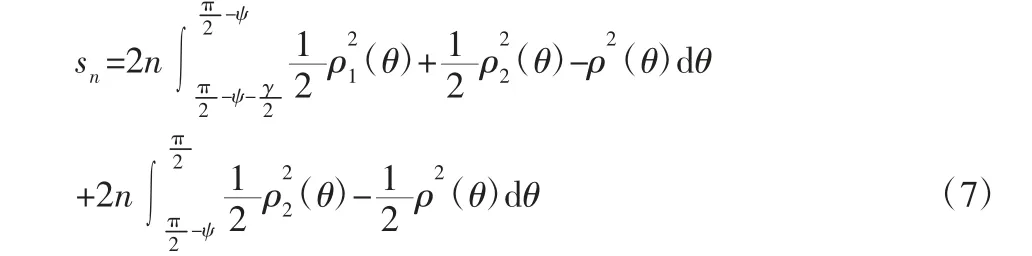
第一个重叠区域中心到工件初始端的距离设为初喷距离g，初喷距离g 对应的涂层厚度之和为sg，g与d 相关，因此sg需要分段讨论：

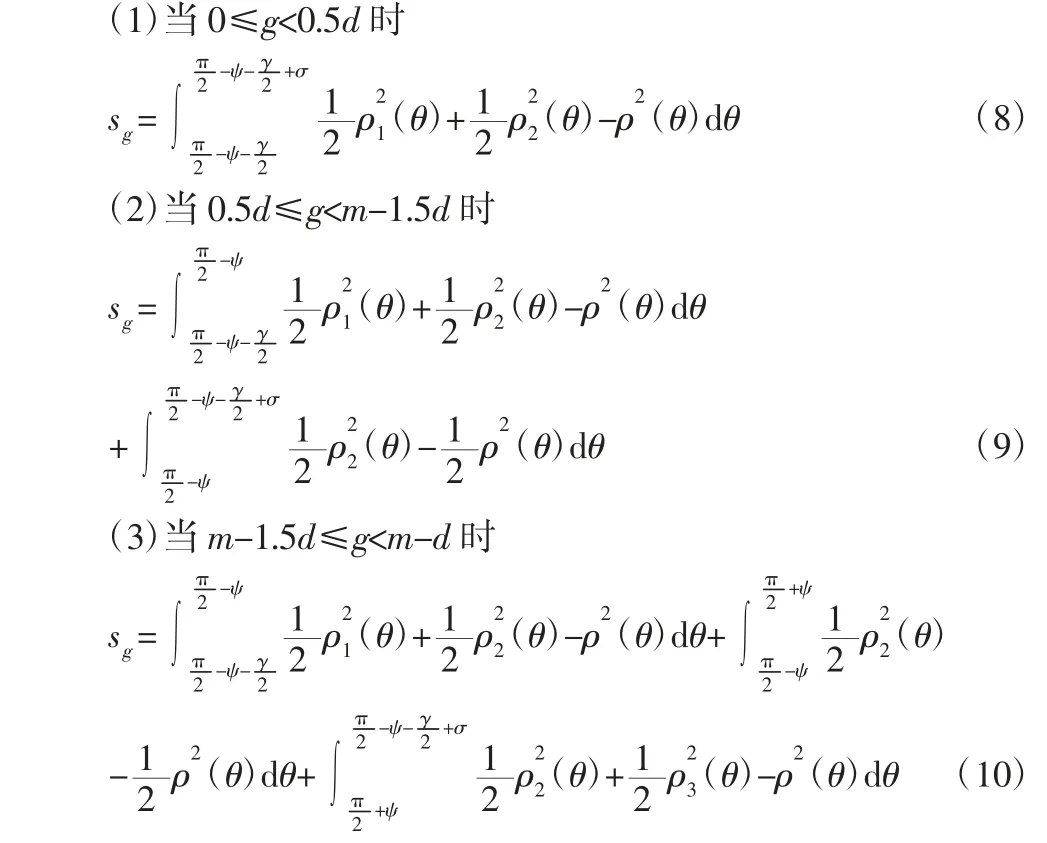
其中，σ=g/R。

最后一个重叠区域中心到工件终点端的距离为终喷距离r，r=l-g-n（m-d），终喷距离r 对应的涂层厚度之和为sr，由于r 同样与d 相关，因此sr也需要分段讨论，如下所示：

（1）当0≤r＜0.5d 时

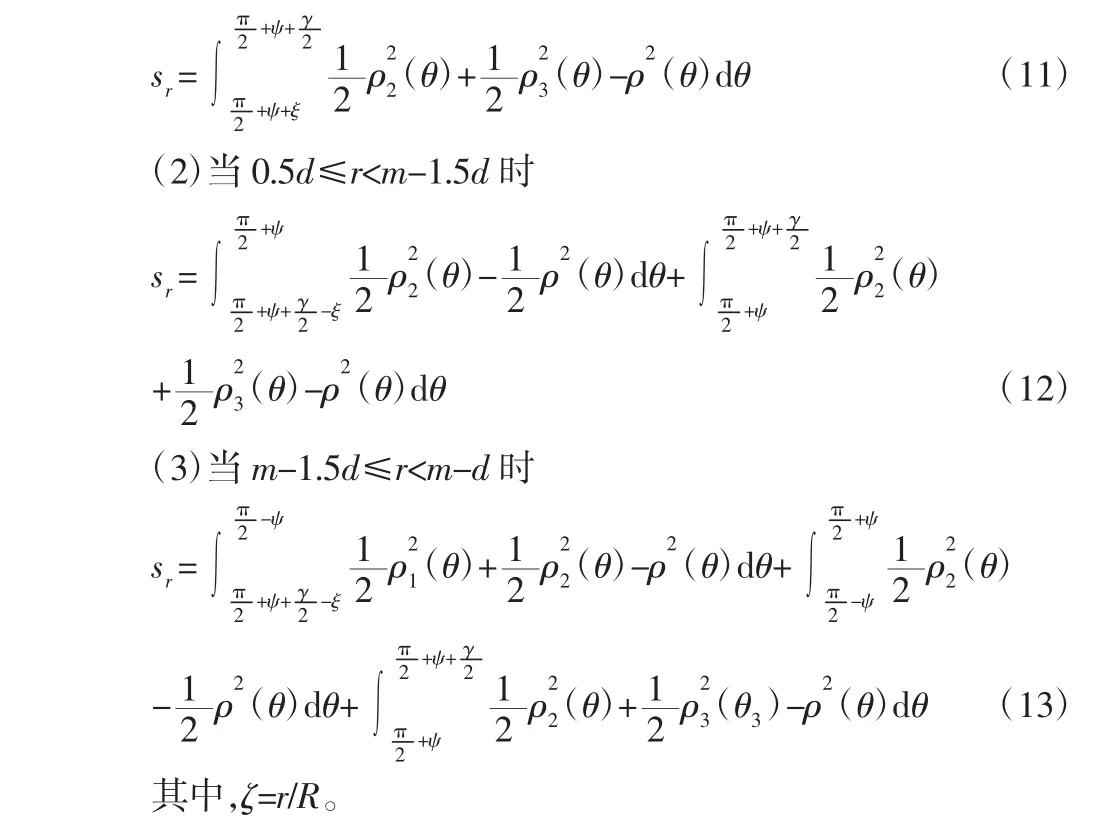
通过上述公式计算得到sn、sg和sr后，计算曲面工件涂层的平均厚度：

4.2 喷涂涂层平均相对偏差函数

与喷涂涂层平均厚度相对应，喷涂涂层平均相对偏差v 也需要分为三个部分vn、vg、vr来计算，其中，vn为n（m-d）区间对应的涂层厚度相对偏差，可用下式计算：

5 曲面涂层生长模型仿真及结果分析

由前文分析可知，涂层的平均厚度f 和平均相对偏差v 均是l、d、g 的函数，但表达式较复杂，不能直观看出它们之间的关系，因此通过MATLAB 软件分别仿真给出f 和v 同l、d、g 的关系，进而验证模型的有效性。

5.1 参数l、d、g 对f 的影响

当l=πR，R＝6 时，平均厚度f 随d，g 的变化关系，如图2 所示。

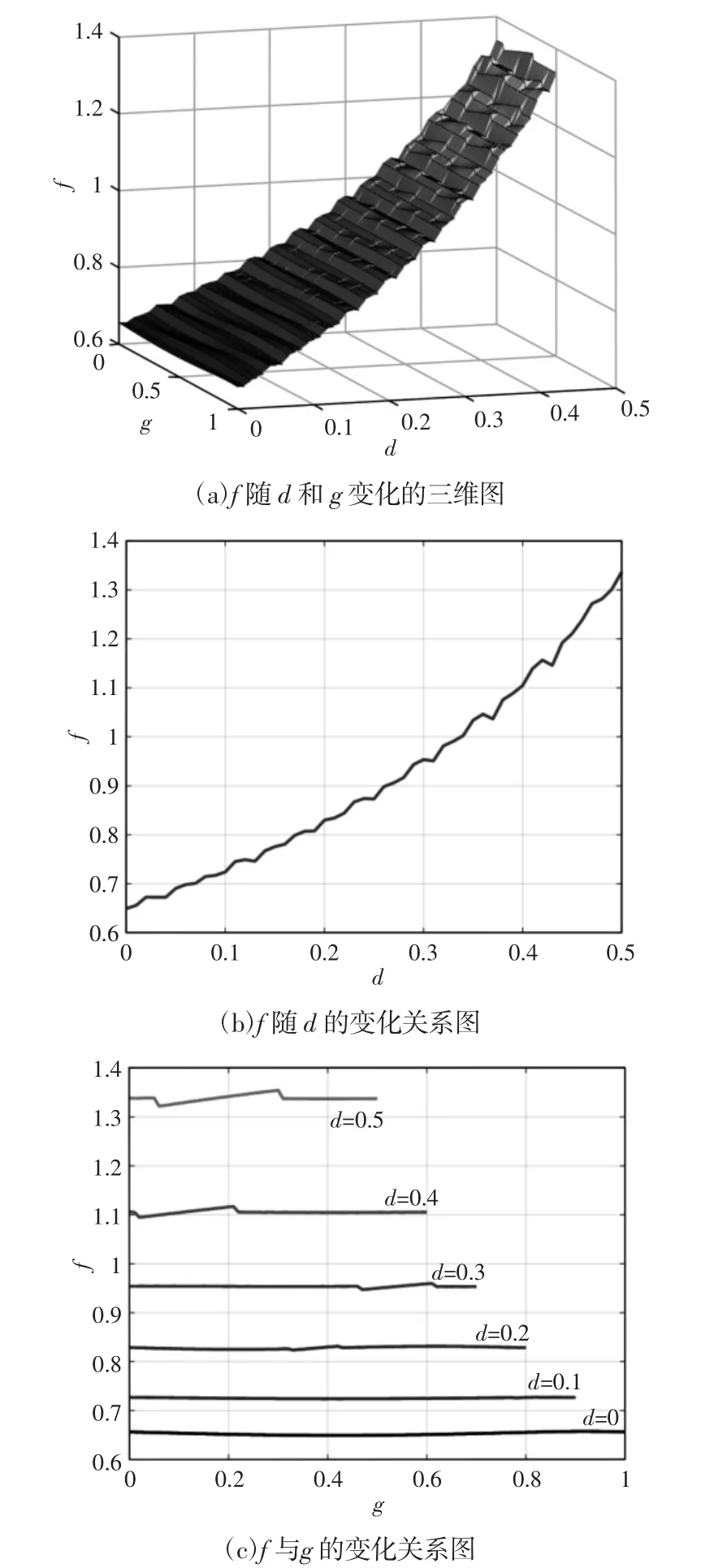
图2 f 与d 和g 的关系图（l=πR，R=6）Fig.2 Relationship Diagram of f with d and g

图2（a）为f 随d，g 变化的三维趋势图，当l 为其它值时，f 随d，g 的变化关系与图2（a）类似。图2（b）为g=0.4 时，f 随d 的变化关系图，图2（c）为d 分别取0，0.1，0.2，0.3，0.4，0.5 时，f 随g 的变化关系图。从图2（a）和图2（b）中可以看出，当l，R 为定值时，平均厚度f 随着d 的增大而变大，当d=0 时，平均厚度f 取得最小值为0.6494，当d=0.5 时，平均厚度f 取得最大值为1.3545。同时从图2（c）中可以看出，对于固定的d 值，平均厚度f 几乎不随g 的变化而变化。

通过以上分析可以得出，d 的变化对平均厚度f 的影响较大，g 和l 对平均厚度f 的影响较小，由此可得，d 是影响平均厚度f 的主要因素，g 和l 是次要因素，在进行曲面工件喷涂作业时应优先考虑主要影响因素d，可以适当忽略次要因素。

5.2 参数l、d、g 对v 的影响

当l=πR，R＝6 时，平均相对偏差v 随d，g 的变化关系，如图3 所示。

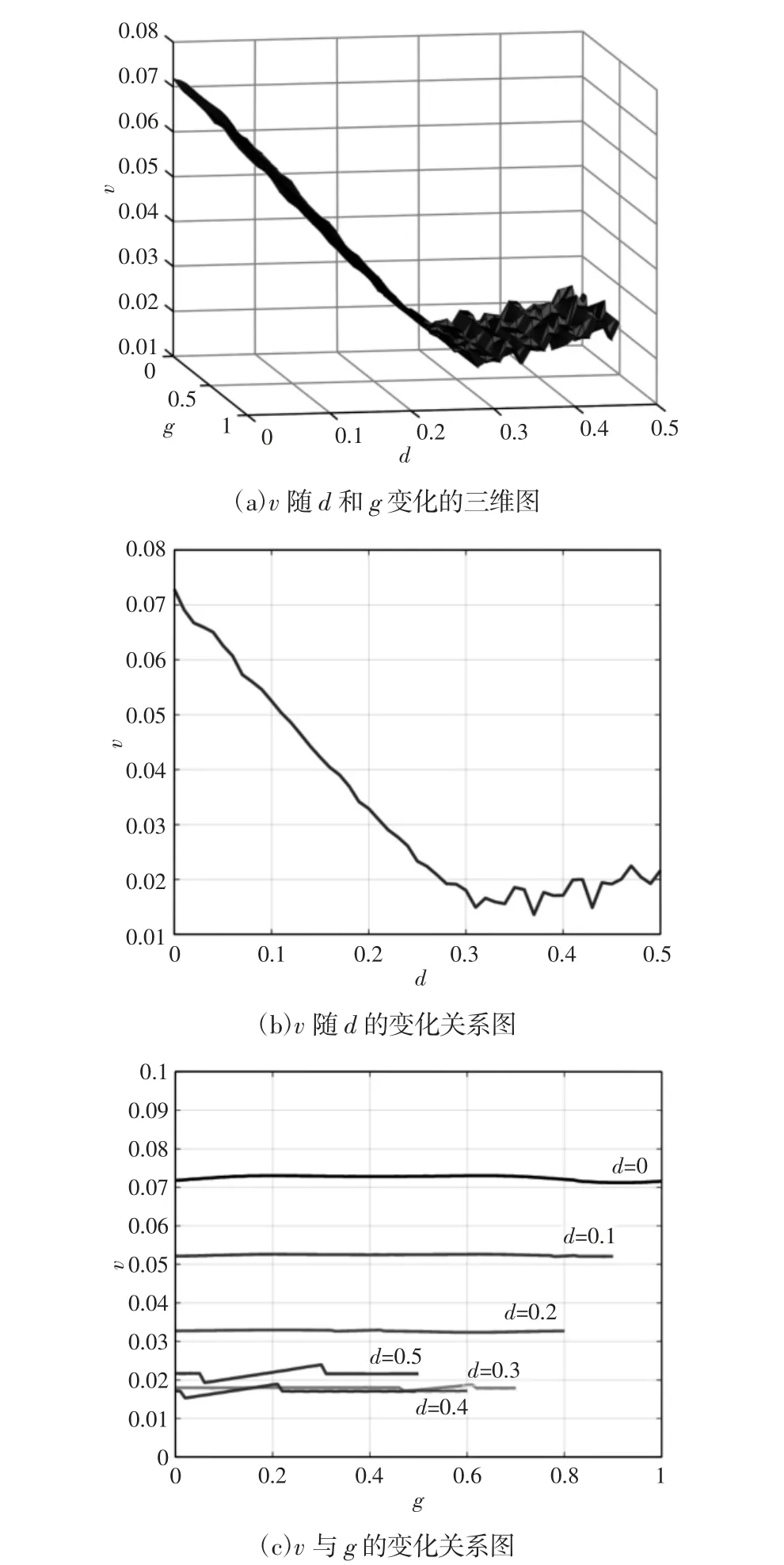
图3 v 与d 和g 的关系图（l=πR，R=6）Fig.3 Relationship Diagram of v with d and g

图3（a）为v 随d，g 变化的三维趋势图，当l 为其它值时，v随d，g 的变化关系与图3（a）类似。图3（b）为假定g=0.4 时，v 随d的变化关系图，图3（c）为d 分别取0，0.1，0.2，0.3，0.4，0.5 时，v 随g 的变化关系图。从图3（a）和图3（b）中可以看出，当l 为定值时，平均相对偏差v 随着d 的增大先逐渐减小后缓慢增大，但随着g的变化，平均相对偏差v 的值变化较小，当d=0 时，平均相对偏差v 取得最大值为0.073，当d=0.37 时，平均相对偏差v 取得最小值为0.013。同时从图3（c）中可以看出，对于固定的d 值，平均相对偏差v 几乎不随g 的变化而变化。

由以上分析可以得出，d 是影响平均相对偏差v 的主要因素，g 和l 的影响很小，因此在曲面工件喷涂轨迹规划时，需要着重考虑d 的变化对平均相对偏差v 的影响。

5.3 曲率半径R 对f 和v 的影响

分析曲率半径R 对f 和v 的影响，在d=0.2、g=0.2 的情况下，f 和v 随R 变化的关系曲线，如图4 所示。

图4 f 和v 随R 变化的关系图Fig.4 Relationship Diagram of f and v change with R

从图4 中可以看出，当d 和g 为定值时，平均厚度f 随R 的增大而逐渐增大，平均相对偏差v 随R 的增大而逐渐减小，说明工件的曲率半径也是影响喷涂均匀性的主要因素。在相同喷涂参数条件下，曲率半径越大，即工件曲面趋于平面时，平均相对偏差越小，喷涂越均匀。

6 结语

针对以航空发动机风扇叶片燕尾基座为代表的曲面喷涂问题，建立了曲面涂层生长模型，提出利用涂层厚度平均相对偏差作为评价函数进行均匀性评价；给出涂层厚度平均相对偏差和初始行程、重叠宽度、工件长度和曲率半径的关系函数，通过MATLAB 仿真出平均相对偏差和各参数之间的关系曲线；仿真结果表明，重叠宽度和工件曲率半径是影响涂层均匀性的主要因素，初始行程和工件长度的变化对涂层均匀性影响很小，在喷涂轨迹优化过程中，可以只考虑重叠宽度和工件曲率半径。所提出的曲面涂层生长模型是正确的，采用平均相对偏差表征均匀行而进行喷涂均匀性分析的方法是有效的，为喷涂轨迹优化和提高机器人喷涂的均匀性提供了理论基础。