新型多履带全向爬壁机器人结构设计

王明强，陈 锦，方海峰，范纪华

（江苏科技大学机械工程学院，江苏 镇江 212003）

1 引言

目前，将可以在船体壁面上工作的机器人，即机器人有机结合地面移动技术和壁面吸附技术，称之为爬壁机器人，其结构与控制的设计成为了当下机器人领域研究的热点之一[1]。爬壁机器人的行走方式有：履带式、足式、轮式以及轮履复合式；吸附方式主要分为真空吸附式、磁吸附式和仿生吸附式。其中，履带式相比轮式有着行走更加稳定的优势。磁吸附分为电磁吸附和永磁吸附两种，而电磁吸附相较永磁吸附而言，有着“断电即断磁”的安全隐患[2]。永磁吸附履带式机器人的主要优势有对壁面良好的适应能力，行走稳定性出众，可以广泛应用于恶劣工况下[3]。因此，国内外对此展开了大量的研究。早在上世纪70 年代，日本及欧美等国的学者便在履带式爬壁机器人的结构方面和试验方面做了大量研究。文献[4]学者也于上世纪90 年代开展了用于壁面爬行的检测机器人和高楼壁面清洗作业的爬壁机器人。

履带式爬壁机器人的转向方式是通过采用左右两条履带的差速实现的，这样不仅会使转向效率变低，达不到精确转向，学者在对履带的运动过程进行动力学分析中也会遇到难点。文献[5]论述了爬壁机器人的动力学建模、仿真和试验，但忽略了机器人转向中心会在转向时出现偏移的影响，不能准确地反映出机器人的转向规律。文献[6]建立了履带式爬壁机器人转向运动学模型，虽然模型中考虑了转向中心偏移的情况，但偏移量并未给出具体计算公式，且理论研究结果与相关文献的实验结果相差较大。此外，永磁吸附履带式机器人通过磁吸附单元来提供吸附力，这就要求了吸附力需要保证机器人的安全性和稳定性，但也不能过大，否则就降低了机器人的灵活性。船体表面上的斜率不同，这也就导致了爬壁机器人最小许用吸附力的不同，同样会对机器人的动力性能产生影响[7]。

提出一种多履带全向爬壁机器人，在进行动力特性分析中，需考虑起伏不平的船体表面，船壁的不同位置和船壁不同的倾斜角度对所需吸附力的影响，而无需考虑机器人转向时产生转向阻力矩及相关因素。通过对多履带全向爬壁机器人停留在船舶壁面上的静止状态进行力学分析，得出在不同工况下其吸附力的变化，然后对其爬壁状态进行力学分析，以确定电机的输出转矩，确定电机和减速器的型号和参数，保证安全可靠吸附能力和壁面灵活能力的基础上，改善和提高多履带柔性爬壁机器人的运动特性并为机构优化设计与运动控制提供理论研究基础。

2 多履带全向爬壁机器人结构设计

多履带全向爬壁机器人移动平台的设计目标是其能够在船体壁面上自如的行进，抛弃了传统的履带差速转向方式，避免了机器人运动过程的转弯趋势，从根本上解决了多履带柔性爬壁机器人在船体表面上的无死角移动，下图为机器人结构示意，如图1 所示。

图1 多履带爬壁机器人示意图Fig.1 The Multi-Crawler Omni-Directional Wall-Climbing Robot Schematic Diagram

采用四条履带包围模式，且履带链接都是由小径双盖滚珠轴承（简称小轮）、小轮轴紧固件、小轮轴和磁性链接体组成。机器人沿着Y 方向进行时，1，3 履带上的小轮通过自身的转动避免了1，3 履带对于2，4 履带行进的阻碍作用，而2，4 履带在行进时，安装于其上的小轮没有转动趋势，不会进行X 方向的滑移，其X方向的运动被1，3 履带上的小轮所限制，及利用了小轮限制了其自身轴向方向的运动，如图2 所示。通过这一原理设计了此方案。此种结构可以在平面上进行全方位移动，抛弃了传统的履带差速转向方式，从根本上解决了多履带全向爬壁机器人在船体表面上的无死角移动。机器人动力学模型成立条件：多履带全向爬壁机器人可以在不同斜率的船体表面上进行直线上下爬行。即要求机器人的驱动转矩和吸附力满足要求。

图2 多履带爬壁机器人结构简图Fig.2 Schematic Diagram of Multi-Crawler Omni-Directional Wall-Climbing Robot Structure

3 静态稳定性分析

磁吸附式爬壁机器人在船体壁面上行走时，不仅需要可靠的吸附能力，而且需要尽可能的提高其运动灵活性，将爬壁机器人作静态稳定性分析，分析爬壁机器人可稳定行走的最小吸附力与船体壁面倾角之间的关系，进而对爬壁机器人的结构做进一步的优化[8]。为了便于分析，如图3 所示。由于实际中的船体表面与Y 轴夹角为负的情况不多，且倾角ɑ 为负时对机器人的可靠吸附是有利的，因此在爬壁机器人的静稳性分析中对ɑ 为负时的受力情况可不做考虑，只考虑倾角ɑ 为正时的受力情况，即α∈［0，π/2］。

图3 受力分析示意图Fig.3 Force Analysis Diagram

将重力G 分解为y 轴和z 轴分量，如图3 所示。

对机器人模型进行受力分析，发现机器人静止在壁面时有以下两种情况，可以导致机器人脱离船体表面。

（1）沿壁面下滑；

（2）绕本体下边纵向翻转。

3.1 以不沿壁面下滑的静力分析

机器人静止于船体表面时，由于自身的重力作用，会有沿壁面下滑的趋势，如图3 所示。而履带接触壁面的四组履带模块提供足够大的静摩擦力，静摩擦力的大小由磁吸附单元所提供的磁吸附力决定。所以为保证机器人不沿壁面下滑，应满足条件：式中：fij—壁面和履带之间的最大静摩擦力，下标i 代表前后履带，j 代表左右履带；Nij—壁面对履带的法向支持力，下标i代表前后履带，j 代表左右履带；μs—壁面和履带之间的最大静摩擦系数；Fm—磁吸附单元提供的磁吸附力。

通过式（3）可知：吸附力的大小由机器人自重和履带与壁面间的静摩擦系数所决定，且可通过增大静摩擦系数或者减小自重来提高机器人抗下滑的能力。

3.2 以抗本体纵向翻转的静力分析

机器人本体纵向翻转的趋势是由自身重力对本体下方履带模块存在的倾覆力矩所产生的。设机器人重心距离壁面的高度为H，单组履带垂直距离为L，列出力矩平衡方程：

以上我们对沿壁面下滑和绕本体下边纵向翻转两种失稳情况进行了分析，得出了关于磁吸附力在不同倾角下以及机器人本体结构尺寸之间的关系，通过分析可知，只需机器人满足以上磁吸附力的要求，即可保证吸附稳定和可靠行走。考虑到机器人作业在户外工况下，会有一些风阻外力因素以及一些不确定影响因子，因此引入安全系数κ=1.4，则可得到爬壁机器人在不同的壁面倾斜角度下与所需磁吸附力最小许用值之间的关系为：

根据多履带爬壁机器人的初始尺寸数值：G=171N，L=600mm，l=80mm，H=60mm，代入式（6），利用数值仿真，得到磁吸附力与船体表面倾角之间的关系，如图4 所示。

图4 抗壁面下滑和抗纵向翻转的最小许用磁吸附力仿真曲线Fig.4 The Minimum Allowable Magnetic Adsorption Simulation Curve of Anti-Wall Slide and Anti-Longitudinal Flip

4 运动受力分析

将爬壁机器人在结构上看作一个可移动的整体，机器人在壁面做直线运动，故两侧履带模块速度相等。对机器人沿直线向上爬行和向下爬行进行力学分析，可以看作驱动力矩、阻力矩和重力转矩之间的关系。

4.1 机器人向上爬行运动分析

因为多履带爬壁机器人无需考虑转向问题，所以默认机器人在移动过程中与水平方向的夹角始终为。则机器人的履带驱动力矩需克服磁吸附单元提供的吸附力和履带上小轮与地面的支持力形成的阻力矩以及自身重力产生的转矩。

根据上面分析得出下式：

式中：MQ—机器人的履带驱动力矩；

Mf—履带上小轮与地面的支持力形成的阻力矩；

MG—自身重力产生的转矩

式中：b—吸附中心和几何中心的垂直距离，取10mm。

通过数值仿真分析，可得当船体表面倾角在0°时，所需电机驱动转矩最大，为15.61N·m。实际y 方向为两侧履带同步驱动，取扭矩分配系数为λ=1.5，则单侧驱动力矩为：

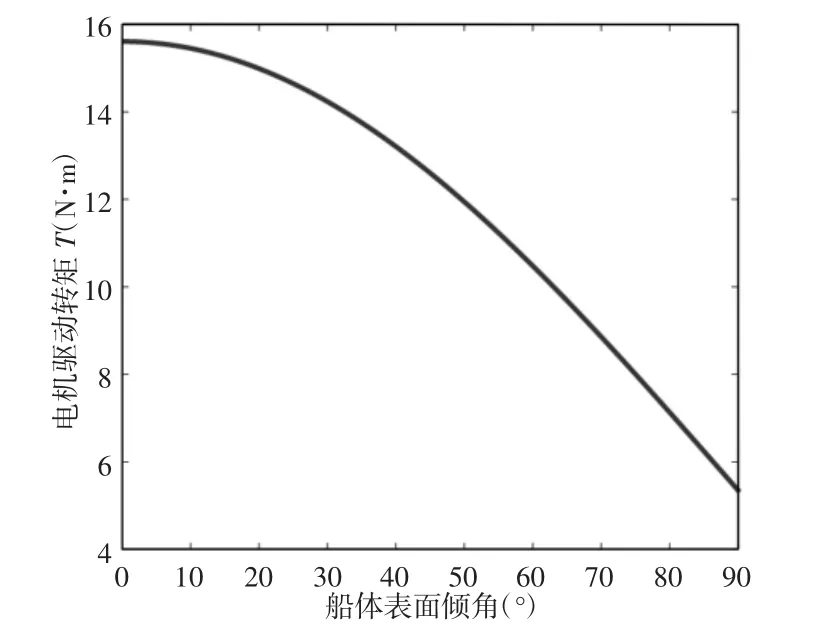
图5 机器人可靠行走最小许用电机驱动转矩仿真曲线Fig.5 Reliable Robot Walking the Small Motor Driven Torque Simulation Curve

4.2 机器人向下爬行运动分析

机器人向下爬行时，同样看作驱动力矩、阻力矩和重力转矩之间的关系，而此时吸附力与支持力形成的阻力矩成了阻止机器人纵向翻转的正向驱动，如下式所示：

可以看出，机器人在向上爬行时，电机所提供的驱动力矩更大，在进行电机和减速器选型时，则只需参考向上爬行时所得到的驱动力矩。

5 样机试验

5.1 电机和减速器的选择

步进电机和伺服电机本质上的最大区别在于开环和闭环，而爬壁机器人在运行过程中需要满足一定的位置精度要求，故在电机选型中，将机器人的动力源选择为直流伺服电机。

通过与类似生产机械所用的电机进行对比，并查阅相关手册，选定了电机和减速器的型号，如表1 所示。

表1 电机和减速器的型号及参数Tab.1 Type and Parameters of Motor and Reducer

电机经减速器传动的效率为η，则减速器的输出力矩、功率应满足：

由计算可知，所选电机及减速器满足条件。

5.2 样机搭建及验证

爬壁机器人能够可靠吸附及稳定行走是实现作业功能的前提。因此在测试前先进行机器人吸附可靠性测试，下图为倾角约26°处的吸附效果图，如图6 所示。由上述静力学分析结果可知，机器人吸附于壁面倾角26°处所需吸附力最大，结果显示机器人能够可靠吸附，并未发生滑落。

图6 样机吸附示意图Fig.6 Schematic Diagram of Sample Adsorption

结合样机试验进行验证，主要是通过爬壁机器人由初始位置行走船体表面上任意位置的过程中时，判断其是否能够可靠行走，另通过采集电机驱动器实时输出电流值，对不同倾角下的电机扭矩值进行检测。首先样机由A 点横向行走到B 点，再由B 点竖直行走到C 点，最后由C 点竖直行走到D 点，即利用简单的路径规划避免运动过程的转弯动作，如图7 所示。

图7 样机试验图Fig.7 Test Diagram

机器人横向行走由A 点至B 点，行走距离约1m，行走耗时20s，机器人竖直向下行走由B 点至C 点，行走距离约0.6m，行走耗时13s，竖直向上行走由C 点至D 点，行走距离约0.6m，行走耗时15s，在行走过程中不存在任何失稳情况，且电机所提供的实时扭矩满足机器人行走的驱动要求，能够可靠吸附并行走，所以力学模型建立与分析是可行的，如表2、图7、图8 所示。

表2 机器人行走试验结果Tab.2 The Results of the Robot Walking Test

图8 电机扭矩实时采集Fig.8 Motor Torque Real-Time Acquisition

6 结论

（1）设计了一种多履带全向磁吸附式爬壁机器人，该机器人抛弃了传统的履带差速转向方式，避免了机器人运动过程的转弯动作，从根本上实现了多履带磁吸附式爬壁机器人在船体表面上的无死角移动。（2）通过对机器人的静态稳定性分析，建立多履带爬壁机器人在两种失稳情况下的力学模型，并利用数值分析，得知当船体表面倾角为26.2°时，机器人所需吸附力最大，且许用磁吸附力要求约535.3N。对机器人做运动受力分析，确定了不同倾角下履带所需的驱动转矩，其中竖直行走时，机器人最小许用电机驱动转矩最大，为15.61N·m。（3）通过搭建样机进行试验，验证了机器人在“危险角度”上能够可靠吸附；在实际行走过程中，电机提供的实时扭矩满足其驱动要求，可以稳定行走。该分析结果为多履带爬壁机器人的设计和优化提供了基础。