提升机现场数据的载荷预测模型研究

郑 彤，杨兆建，杨 波

（1.太原理工大学机械工程学院，山西 太原 030024；2.煤矿综采装备山西省重点实验室，山西 太原 030024）

1 引言

矿井提升系统是连接煤矿井下和井上的重大固定设备之一，其动力学特性和提升能力是煤矿生产的重要影响因素[1]。随着煤矿资源的开采和科学技术提高，对提升机也提出了更高的要求。为了保证提升机运行过程的稳定性和安全性，提升机的载荷测量就显得尤为重要。目前，人工神经网络（Artificial Neural Network）在载荷识别领域表现不俗，并且广泛应用于故障诊断、数字识别、以及载荷参数识别等领域[2]。

文献[3]针对水电厂房结构的震动响应使用LM 优化的BP 神经网络进行动态识别。文献[4]采用GA 的BP 模型成功的以较高的精度识别了飞行载荷。文献[5]运用递归神经网络算法对直流电机的负载进行了分析并与之前的文献所述方法进行了对比。文献[6]使用神经网络来识别钢丝绳载荷模型。同时也有许多学者针对提升机的载荷辨识进行了研究。文献[7]建立了矿井提升系统的动力学模型，通过模态分析方法计算得出系统的动态特性参数，并讨论了不同工况下的动载响应特性。文献[8]从仿真角度分析了速度曲线下各种典型载荷的运行特性和载荷特性之间的关系。以某矿副立井JKM-2.8×6（I）A 型井塔式多绳摩擦式提升机为研究对象，应用多种神经网络模型进行训练和载荷预测，并且进行了对比。

2 神经网络结构

BP（Back Progagation）神经网络是目前应用最广泛的神经网络之一[9]。三层BP 网络的拓扑结构，如图1 所示。这种神经网络的特点是：各个神经元是无反馈连接的，且各内层神经元之间没有任何联接，只有相邻的神经元之间是联接的。

RBF（Radial Basis Function）神经网络是基于人脑神经元细胞对外界的局部性而提出的，是一种新颖而有效的前馈式神经网络，具有比较高的运算速度和非线性映射功能[10]。RBF 是一种三层前馈网络（类似图1），不同的是神经元的作用函数为radbas（高斯函数）。它的优点是学习速率很快。

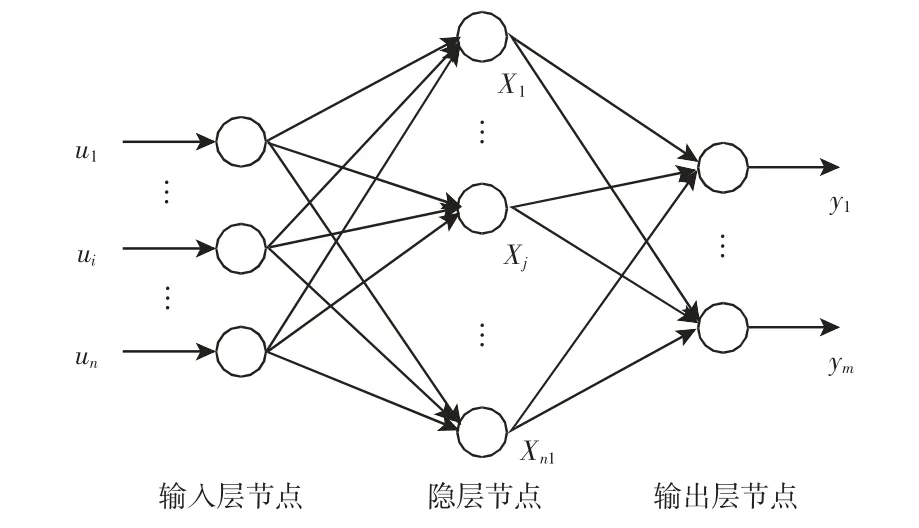
图1 BP 神经网络结构Fig.1 BP Neural Network Structure

Elman 神经网络与传统的静态前馈神经不同，它具有一个连接层[11]，有了这个连接层便可以构成局部反馈。并且由于连接层的传递函数是线性函数，多了一个延迟单元，造成连接层对于过去的状态是有记忆功能的，并与网络输入一起作为下一时刻的隐函数的输入，因此让Elman 网络是一种具有动态记忆功能的神经网络。一般是用于时间序列的预测问题。网络结构，如图2 所示。

图2 Elman神经网络结构Fig.2 Elman Neural Network Structure

3 提升机数据选取及相关性分析

3.1 提升机设备简况及动力学方程

试验对象选择的是JKM2.8×6（I）A 型多绳提升机，用于马兰矿副立井主要承担升降工作人员与井下设备、提升矸石等工作。现场设备布置，如图3 所示。

图3 JKM2.8×6（I）A 型多绳提升机Fig.3 The JKM-2.8×6（I）A Multi-Rope Friction Hoist

提升系统图，如图4 所示。由于对数据进行初步分析，提升机上提重载和下放重载对应的数据有较大差异，因此区分提升和下放进行动力学分析如下：

如图4（b）所示下放重载时两侧钢丝绳的张力差为：

式中：Fsj—提升侧钢丝绳张力；

Fxj—下放侧钢丝绳张力；

Q—载荷；

Qz—容器自重；

m、n—主绳根数、尾绳根数；

p、q—单根主绳重量、单根尾绳重量；

Δ—主、尾绳单重差，Δ=mp-nq；

Hc—钢丝绳悬垂长度，Δ=Hc+Hk+Hh；

Hk—提升容器至主轴中心高度；

Ht—提升高度；Hh—尾绳高度；

h—容器下放或提升距离；

ws、wx—上升侧和下放侧的矿井阻力，对于罐笼取0.1Q，箕斗取0.075Q；

K—矿井阻力系数，对于罐笼取1.2，箕斗取1.15。

图4 提升系统图Fig.4 Lift System Diagram

可以看出，提升与下放时的载荷有区别的，因此应该区分提升和下放数据进行分析。以提升工况为例进行分析。

3.2 现场数据获取及相关性分析

所谓现场数据，就是提升机提升时的实时数据以及载荷数据，这里的载荷主要是指两根钢丝绳的张力差，统计方法是统计每次对应提升人或者矸石的重量，每人按照70kg 约算。研究中选取了具有代表性的易量化处理的运行系统数据和电控系统的15种数据。通过SPSS19.0 软件相关性分析，采用皮尔逊相关系数计算负荷与其影响因素的相关系数。

所得载荷影响因素的原始数据，如表1 所示。

表1 原始数据Tab.1 Raw Data

4 自适应BP 神经网络构建

4.1 确定模型的输入输出向量

以上述的八种工况数据为输入变量，提升过程中载荷为输出变量。随机选取2000 条数据为训练样本，剩余的200 条数据为测试样本。

4.2 数据预处理

数据预处理是为了解决实际得到的数据的不完整或者脏数据的问题。通常采用的数据处理方法有两种，一种是数据归一化属于数据变换，另一个是PCA 数据降维，属于数据归约。

由于数据单位和量级不同，为了避免训练过程中因数据原因而造成过大的网络训练误差。需要对数据进行预处理。目前最为常用的方法是最大最小法，即将所有的数据转换到0 和1 之间，函数形式如下[12]：

式中：xmin—数据序列中的最小值；xmax—序列中的最大值。

4.3 确定网络层数和隐含层节点数

BP 神经网络包含一个或多个隐含层。已经有理论上证明，单个隐函层的网络可以通过适当的增加神经元节点的个数实现任意非线性映射。因此，采用了单隐含层前馈网BP 网络。

隐函数的选择对BP 神经网络非常重要，直接影响了训练误差和训练时间。一般采用如下经验公式估计[13]：

式中：c—隐含层节点数；m—输入层节点数取8；n—输出层节点数取1；a—1～10 之间的常数。因此取值范围为［4，13］。在确定了传递函数和训练函数的情况下，对样本集进行不同节点数的训练结果，如图5 所示。

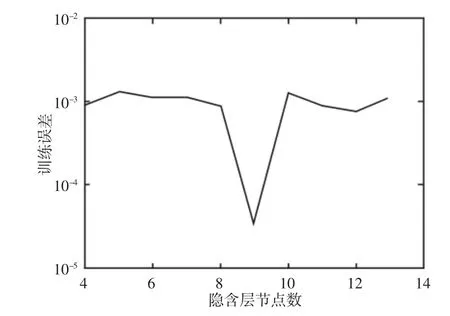
图5 节点数对训练误差的影响Fig.5 The Influence of Nodes on Training Error

可见，当隐函数节点数为9 时，训练误差最小。

4.4 选择合适的传递函数和训练方法

传递函数选择：传递函数是BP 神经网络的重要组成部分，传递函数的选择直接影响到训练的正确性和准确度。传递函数总体上分为三类：线性传递函数、非线性传递函数、阈值传递函数等。在本例中，经过误差对比选择隐含层函数为tansig 输出层函数为purelin。训练函数的选择：经过对比几种训练函数Trainlm函数训练速度快效率高，所以选择它为训练函数。

4.5 结果及分析

构建了自适应BP 神经网络，输入层为提升机运行过程中8 种数据，输出层为对应提升过程的载荷。经过多次优化计算，神经网络的结构参数为：输入层节点数，隐含层节点数，输出层节点数分别为8、9、1。设定网络的训练函数为Trainlm，学习函数为Learngdm，学习率0.07，迭代最大次数1000，目标精度0.000000001，动量因子是0.8。采用2000 条数据训练设置好的BP神经网络，网络在第15 步取得收敛，运行时间0.3s，其性能曲线，如图6 所示。

图6 BP 神经网络训练Fig.6 BP Neural Network Training

利用训练好的网络对提升机载荷进行识别。随机选取200组提升过程中的运行数据和电控数据，对载荷进行预测，预测结果，如图7 所示。绝对误差和相对误差，如表2 所示（随机选取五组展示）。

图7 BP 神经网络预测结果Fig.7 Neural Network Prediction Result

从表2 和图7 可以看出，BP 神经网络对于现场提升机载荷的预测具有非常大的优势，相对误差控制在4%以内。并且经过权重计算，如表3 所示。加速度段主电机电流平均值所占权重约为0.32，而最大启动电流、平均加速度、平均减速度所占权重最小约为0.04。表明，根据BP 神经网络建立的此载荷模型，加速度段主电机电流平均值对载荷预测的结果影响最大。

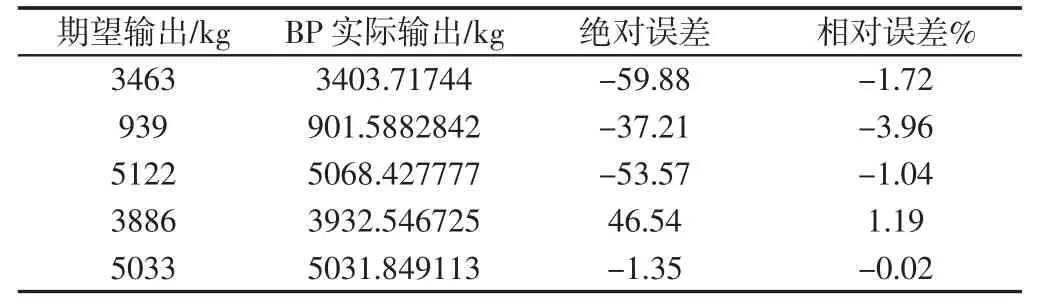
表2 绝对误差和相对误差Tab.2 Absolute Error and Relative Error

表3 输入数据的权重Tab.3 Input Data Weight

5 预测结果对比

RBF 神经网络选择中心节点为25，中心宽度1.4。Elman 神经网络选择最优隐函数节点数为16。RBF 和Elman 神经网络的训练结果分别，如图8、图9 所示。利用RBF 神经网络对提升机现场数据的训练，在第25 步取得收敛，而Elman 神经网络在第114步取得收敛，并且均方误差均＞BP 神经网络所得到的10-3。利用RBF 和Elman 神经网络的平均相对误差为5.31%和11.69%可见，与RBF 和Elman 神经网络相比，在此问题上自适应BP 神经网络更具有优势，如表4 所示。

图8 RBF 神经网络训练Fig.8 RBF Neural Network Training

图9 Elman 神经网络训练Fig.9 Elman Network Training

表4 三种神经网络误差对比Tab.4 Comparison of Three Neural Network Errors

6 结论

（1）数据源为提升机现场的大量数据，利用大数据和SPSS软件提取出影响载荷的特征数据，并建立神经网络，指出一种可以识别提升机动态载荷的方法。

（2）与其他两种神经网络相比，在处理提升机现场数据时，学习率自适应的BP 神经网络可以得到更为满意的载荷预测精度，平均相对误差为3.57%，而利用RBF 和Elman 神经网络的平均相对误差为5.31%和11.69%，由此可见，采用自适应的BP 神经网络在此问题上优于其他两种神经网络。

（3）基于现场数据的载荷分析可以为摩擦式提升机载荷监测提供参考，也可以进一步为现场的安全生产与维护提供理论参考依据，非常具有现实指导意义。