装载机铲斗强度分析方法研究

杨 宁，李 冰，徐武彬，张继尧

（广西科技大学机械工程学院，广西 柳州 545006）

1 引言

装载机作为应用广泛的土方机械之一，其作业对象通常是碎石、沙子、土壤、粮食等散体物料，装载机铲斗作为与物料直接接触的工作装置，其结构强度和优化设计对整机的工作效率和燃油消耗的影响不言而喻[1]。在全球节能减排和环境保护的大趋势下，工程机械作为排放大户，面对着巨大的压力和挑战，在国内外龙头企业的带领之下，工程机械也走上了节能减排的发展道路，更加注重产品的轻量化等优化设计设计，这就对强度分析理论提出了新的要求。

长期以来，作为引发铲斗等工作装置受力不均、容易变形、疲劳破坏的原因之一，散体物料内部运动以及散体物料与设备体之间的相互作用没有得到充分的关注和考虑，现存的强度分析仅仅是借助有限元的方法，是一种基于理论经验指导的评价方法，即拿经验公式计算得来的数据当作恒定载荷加载到工作装置相关结构中去进行计算[2－8]。这样存在以下问题：（1）虽然能够了解铲斗的整体强度，保证产品的强度在使用范围之内，但是无法满足对铲斗等工作装置结构强度的全面了解和把握，换句话说，该方法只是完成了强度校核的工作，但是并不代表着强度满足要求的同时结构也是最优的；（2）在实际作业中物料和铲斗之间是一种比较复杂的相互作用关系，铲斗物料之间的接触具有高度非线性的特点，模拟结果的可靠性有待进一步研究，那么基于经验法而来的铲斗结构优化也需要重新考虑；（3）有限元法往往局限于小变形的假设，已经不能解决受散体物料作用的铲斗应力和变形问题；（4）该计算方法无法通过实验验证其合理性，现场应用更难以展开。离散元素法的出现，正好解决了这个难题，它能基于接触模型和运动方程获取到散体物料与设备体之间的相互作用力，但是单独使用离散元软件，无法得到结构体对散体物料的响应，即无法观察结构体变形等特征，通过将散体物料对铲斗的作用力提取出来，就能够获得设备体在工作期间受到的动载荷，至于这个动载荷怎么准确加载到相应的有限元软件中观察其力学响应，是离散元－有限元耦合求解的核心问题。

为探讨新的强度分析方法，以某型号小吨位装载机的铲斗为例，从散体力学出发，基于接触模型和运动方程，获取铲斗作业阻力动载荷。其次，根据离散元仿真的可视化，确定铲斗不同时刻的受力位置，并通过有限元法将作业阻力精确施加到节点，了解铲斗工作状态下的真实的强度分布和应力情况并与实测值进行对比。该方法避免了传统强度分析中由于边界条件简化对计算结果带来的干扰，同时通过对应力分布情况进行分析，能为铲斗等土方机械工作装置的结构轻量化设计和选材提供新的参考。

2 离散单元法获取铲斗受力

2.1 颗粒接触模型

离散元素法中的接触模型可以分为线性接触和基于Mindlin 理论的非线性接触两种[9]。由于线性接触模型在实际计算中表现出不稳定的特点，经过多年发展，研究人员提出了很多新的接触模型，如线性变刚度模型、Hertz-Mindlin（no-slip）非线性接触模型等，这些模型相对于线性模型，求解更加合理、稳定。其中Hertz-Mindlin（no-slip）模型也是离散元分析软件中默认的接触模型，它具有计算效率高并且准确的优点，适用于研究常规颗粒间的相互作用，是目前研究中常用的接触模型。因此，本研究选用该模型作为离散元仿真接触模型。其力学模型是一个“弹簧—缓冲配置”。Hertz-Mindlin（no-slip）接触模型，如图1 所示。

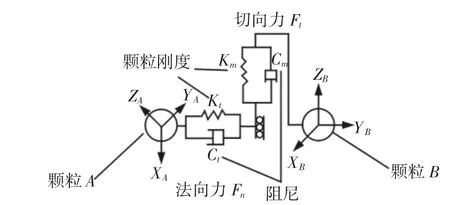
图1 Hertz-Mindlin（No Slip）接触模型Fig.1 Hertz-Mindlin（No Slip）Contact Model

式中：μr—滚动摩擦因数；Ri—质心到所接触点的距离；ωi—物体在接触点处的单位角速度矢量。

在颗粒接触模型确定之后，碎石颗粒之间的接触力便可以通过以上模型和公式计算获得。

2.2 碎石物料模型的建立

由于接触模型中接触力的计算需要对颗粒之间、颗粒与设备体之间的静摩擦系数、滚动摩擦系数、碰撞恢复系数等参数进行定义，并且参数定义越精准，仿真计算的精度越高。为此课题组自制了静摩擦系数测量装置、滚动摩擦系数测量装置、碰撞恢复系数测量装置，对实际作业对象中碎石与碎石、碎石与钢板之间的接触参数进行标定，测量数据，如表1 所示。为了使数值模拟分析中，物料模型更接近实际模型，对实际作业物料堆中碎石物料进行归类研究，选取物料堆中最常见的三种形状碎石，如图2 所示。采用逆向工程原理，使用HandySCAN700 三维激光扫描仪获取三种形状碎石的外表面轮廓，然后在EDEM 中进行填充，课题组做了相关的仿真和试验对比，模型的准确性得到了验证[10]。

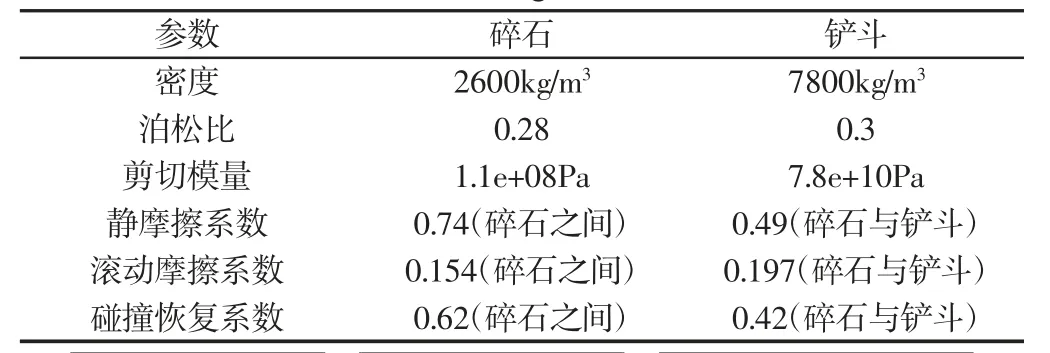
表1 碎石和铲斗的参数设置Tab.1 Parameter Setting of Rock and Bucket

图2 碎石物料形状Fig.2 Shape of Crushed Stone Material

2.3 定义铲斗运动特性

对装载机工作装置进行动力学仿真分析，通过采用滑动副和铰链副的方式对工作装置油缸建立约束，并在滑动副施加插入深度的位移函数来控制工作油缸的运动，得到铲斗的运动特性，其中，x 方向为铲斗绕动臂和斗杆转动的方向，该方向只需定义角加速度，Y 方向为铲斗前进方向，Z 方向为举升方向，如图3 所示，横坐标为铲斗工作过程运动时间，纵坐标为铲斗插入、转斗、提升后退各个阶段的速度值、角加速度值。

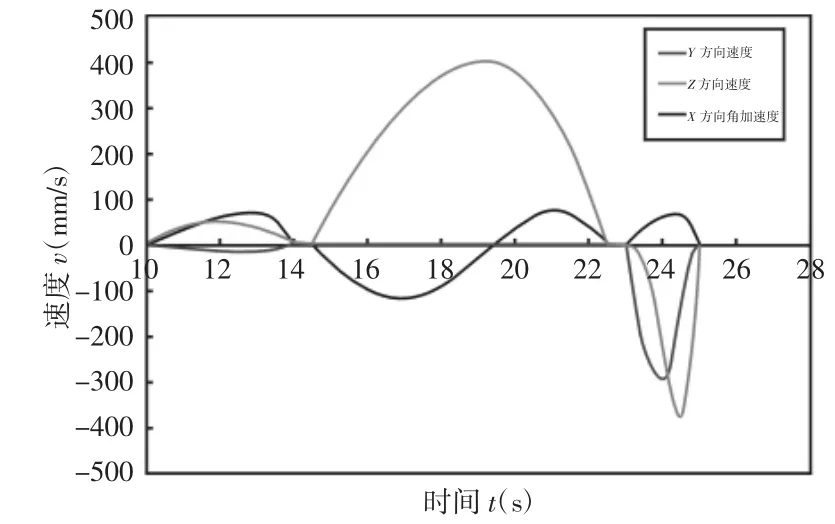
图3 铲斗速度和角速度曲线Fig.3 Velocity and Angular Velocity Curve of Bucket

2.4 离散元仿真获取铲斗作业阻力

颗粒和铲斗的仿真模型及铲斗的运动特性创建完毕之后，需要对离散元仿真中的边界条件进行设置，包括颗粒工厂、仿真时间步长、仿真区域计算网格等。一般设置颗粒工厂为动态生成，产生颗粒的总重量与实测实验中物料堆的质量基本相同；为了兼顾仿真计算精度和仿真效率，设置仿真时间步长为瑞利时间步长的20%；定义网格尺寸为（2～4）倍的颗粒半径；数据保存间隔取0.01s，开始铲斗铲装过程的离散元仿真。

铲斗作业的仿真模拟完成之后，借助离散元方法，基于对碎石之间、碎石与铲斗之间的作用关系，获取铲斗在整个铲装过程中的受力曲线，如图4 所示。输出铲斗节点力数据并采用有限元的方法对铲斗进行强度分析。

从铲斗的受力曲线图可以看出，在插入阶段，随着铲斗插入料堆的深度增加，所受到的阻力不断变大；当插入动作完成，铲斗开始转斗，可以发现此时铲斗受力出现峰值；随着转斗不断完成，斗内物料逐渐滑落，铲斗所受阻力有变小的趋势，最后稳定为斗内碎石的重量。在整个铲装过程中，铲斗所受到的载荷随时间不断变化，是一个动态过程，一定程度上证明了传统分析方法将铲斗受力视为恒定载荷缺乏合理性。

2.5 不同时刻铲斗物料作用位置变化

通过离散元素法仿真，得到了碎石物料之间以及碎石物料和铲斗之间的作用力曲线，同时，借助离散元仿真的可视化功能，可以追踪到铲斗不同时刻受力位置的变化情况，如图5 所示。随着铲斗不断向前运动，碎石物料与铲斗的接触作用位置不断发生变化，可见在整个工作过程中铲斗不同部位所受到的力的大小和方向各不相同，并随时间不断变化，是一个动态过程。不难发现，传统的结构强度计算方法将铲斗的受力位置假设为切削刃上的集中力或者均布力的方式与铲斗实际工作状态下的受力位置和分布存在明显的误差。因此，在对铲斗进行有限元分析时，需要将作用力的大小和位置变化考虑在内。

图5 不同时刻物料在铲斗内的作用位置Fig.5 The Position of the Material in the Bucket at Different Times

3 装载机铲斗结构强度分析计算

离散元仿真只能得到散体物料对铲斗的作用关系，但是无法获得铲斗受到作用力之后的力学响应，即无法观察结构体变形等特征。有限元法作为应用最广泛的数值分析方法，很多工程问题都可以借助有限元法解决。将离散元软件EDEM 和有限元软件ANSYS 进行耦合是一种传统方法无法比拟的分析方法，可以实现强强联合、扬长避短、提高计算精度和效率、扩大应用范围。为此，考虑将离散单元法和有限单元法进行耦合，对铲斗强度计算分析。耦合计算的关键是，需要使接触面上有限单元的节点与离散单元的角点重合，并保证其位移和力的连续，通过节点力和位移的相互传递和循环计算来实现离散元-有限元的耦合。

耦合计算的难点主要表现为单元类型不同：EDEM 只能识别三角形壳单元，ANSYS Workbench 单元类型比较全面，比如三角形壳单元、四面体单元等多种单元类型。为解决上述难题，要保证有限元单元类型和网格大小要与离散单元完全相同，在网格划分方面，Hypermesh 软件功能最为强大，具有导入模型快、几何清理便捷、网格质量高的优点，并且具有强大的导出功能，能导出其它通用软件可接受的文件类型，因此，借助Hypermesh 软件对铲斗模型进行网格划分，并另存为相应的格式文件分别用于离散元和有限元仿真分析。通过对铲斗材料属性和约束进行定义，并对其进行网格划分，将离散元获取的节点力载荷对应施加到铲斗有限元网格节点上，铲斗底板、侧板、刀板、斗壁、挡板均受到一定的作用力，符合实际铲装过程受力分布，说明仿真设置合理。

对铲斗在散体力作用下的力学响应进行求解计算，计算结果，如图6 所示。已知铲斗的材料为Q345，其屈服极限为345MPa。从图中可以看出，铲斗在整个装载作业过程中最大应力为117.05MPa，小于材料的屈服极限，出现在动臂与铲斗铰接的挂耳板处，应力集中区域分布在挂耳板铰孔上下方、斗后壁下方、斗后壁与加强板焊接处、挂耳板与斗耳板连接处等位置，对称性良好。铲斗变形情况可以在图中看出，最大变形量为1.9432mm，发生在铲斗底部前端，经企业调研结果可知，由于插入过程中斗刃需要不断地切削料堆以及满斗情况下转斗需要克服物料的重量等，在实际铲装作业过程中最容易发生变形和磨损的位置就是铲斗底板前端，说明仿真分析与铲斗实工况相吻合。

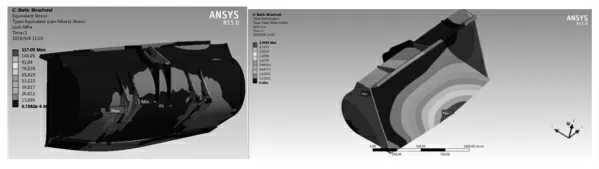
图6 铲斗应力和位移分布云图Fig.6 The Distribution of the Stress and Displacement of Bucket

4 对比验证

为了解装载机铲斗在实际作业中结构强度和应力分布情况，同时验证上述理论计算方法的准确性，对装载机铲斗进行动态应力应变测试，测点布置，如图7 所示（说明：①测试中共选取14 个测点，由图7 可知仿真中最大应力出现在斗底板正下方铲斗铰耳的下方，在实际应力测试中该处与物料发生接触，应变片极易被磨损破坏，所以在其附近选择容易操作的点进行验证；②4#应变花在测试中45°方向破损，数据异常，该点不参与验证）。测试结果，如图8 所示。应力变化趋势与上述得到的铲斗作业阻力变化趋势完全吻合。其中3#测点的实测应力值和理论计算值的对比图，如图9 所示。

图7 测点布置图Fig.7 Layout of Measuring Points

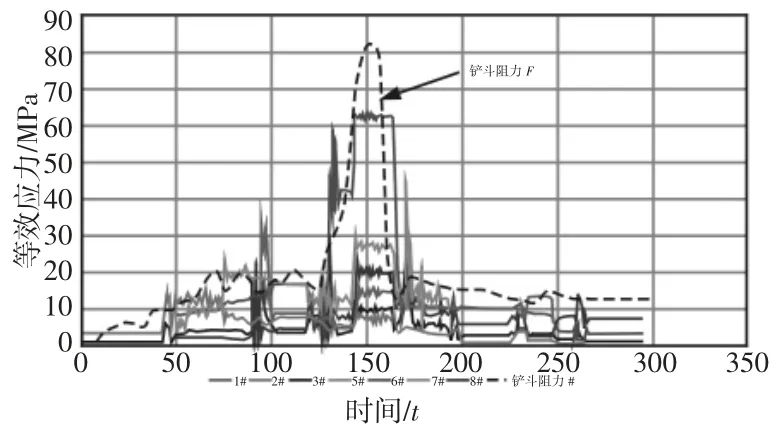
图8 测点等效应力曲线Fig.8 Equivalent Stress Curve of Measuring Points

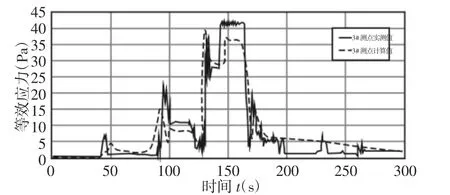
图9 3#测点等效应力曲线Fig.9 Equivalent Stress Curve of 3# Measuring Point

从测点应力对比图可以发现，理论计算值略小于实测应力值，这是因为在仿真中无法考虑到板厚不同或者焊接质量等影响应力计算的因素，虽然两者数值上略微有些偏差，但是从整体变化趋势来看，实测应力值和理论计算值的变化趋势吻合度较高，一定程度上可以验证理论计算的可靠性。另外。虽然由于客观原因，最大应力区没有测到，但是从所选的各个测点实测值和仿真中对应点的计算值比较吻合的情况来看，最大应力区的实测值应该和理论计算值相吻合，或者略大于理论计算值。为了进一步说明传统结构强度计算方法中存在安全系数取值过大，设计偏于保守的通病，下面按照传统的结构强度计算方法对铲斗进行有限元分析。取该型号的装载机额定装载量，按照静力等效原则，作用于铲斗上的最大水平载荷为49kN，最大垂直载荷为56kN，采用传统强度计算方法的六种典型工况对铲斗进行分析，如图10 所示。并将传统强度计算结果与离散元-有限元耦合计算结果进行对比，对比情况，如表2 所示。对比两种计算方法的结果可以发现，传统强度计算应力值明显偏大，并且大于实测应力值，分析其原因主要是铲斗在实际工作过程中所受的外载荷不可能同时达到装载机最大牵引力和崛起力，因此为获得准确的铲斗应力大小和分布情况，必须保证其所受外载荷的数值足够准确合理。同时，载荷的加载位置也需要结合实际情况来确定，因此传统强度计算方法中边界条件的大量假设会导致其计算结果不准确，不能够为后续铲斗优化提供准确的参考。

图10 六种典型工况Fig.10 Six Typical Working Conditions

表2 不同有限元求解方式下铲斗受力情况Tab.2 Force Conditions of Bucket under Different Finite Element Solutions

5 结论

（1）铲斗在作业过程中所受的力并非恒定不变的，而是一个随时间不断变化的动载荷，并且作业阻力不仅只是铲斗切削料堆的阻力、物料与铲斗间的摩擦力和物料自身重力，还包括散体物料之间、散体物料与设备体之间的相互作用力，因此在对铲斗进行有限元分析时需要考虑散体力的存在。

（2）借助离散元素法，得到铲斗受力，解决了传统铲斗有限元计算中载荷需要假设的难题，传统强度计算方法采用极限工况对铲斗进行校核导致设计和选材过于保守。

（3）提出的离散元-有限元耦合计算方法能为铲斗等工作装置的设计研究提供一套全新的设计理念，并且一定程度上可以代替实验验证环节。同时有利于实现产品精品化设计，尤其是在满足强度要求的前提下，可以进行轻量化、经济性等多目标优化设计。