机械臂动力学参数的多变异策略花授粉算法辨识

王 罡，郭芳泽，吴晓仁

（集美大学计算机工程学院，福建 厦门 361021）

1 引言

随着机械臂在高精制造业中的参与，机械臂控制精度要求越来越高，传统的PID 控制难以满足要求，而模型预测控制、前馈控制等先进控制方法的关键在于动力学模型能够准确反应机械臂动态特性[1]。因此，机械臂动力学参数辨识对提高控制精度、降低控制成本意义明显。

基于参数模型的机械臂动力学参数辨识方法可分为非智能方法和智能方法。非智能方法是指最小二乘法、最大似然法及其改进等，此类求解方法不具备算法智能性；智能方法是指遗传算法、人工蚁群算法、粒子群算法等，此类求解方法具备算法智能性。文献[2]设计了机械臂的持续激励轨迹，以回归矩阵条件数最小为指标，此方法提高了参数辨识的精度和速度。文献[3]设计了满足速度、加速度边界约束的改进傅立叶级数作为激励轨迹，使用最大似然法作为参数估计方法，该方法提高了参数辨识精度。文献[4]针对无人机悬停过程中动力学参数辨识问题，提出了混沌蜂群算法的求解方法，提高了参数辨识精度。文献[5]优化了机械表激励轨迹，使用混沌粒子群算法进行参数辨识，辨识精度高于基本粒子群算法。在智能算法快速发展的今天，基于智能算法的动力学参数辨识成为热点，主要集中于三个方面：（1）算法性能的开发，提高算法的求解质量，（2）激励轨迹的设计，激励出所有待辨识参数；（3）模型建立精度的提高，使模型更加符合实际。

研究了机械臂动力学参数的辨识问题，通过合理建模和改善算法性能两个手段提高辨识精度。从理论层面分析了花授粉算法后期进化能力弱、陷入局部最优的原因，将定向变异和均匀变异融入到算法中，提出了多变异策略花授粉算法，达到了提高动力学参数辨识精度的目的。

2 机械臂动力学模型

2.1 PUMA560 机械臂

PUMA560 机械臂的动力学参数已知，可以对后文的辨识结果进行精度评价，因此选择PUMA560 机械臂作为研究对象。PUMA560 机械臂系统具有6 个转动关节，前三个关节角决定腕部位置，后三个关节角决定腕部姿态[6]。PUMA560 机械臂模型，如图1 所示。

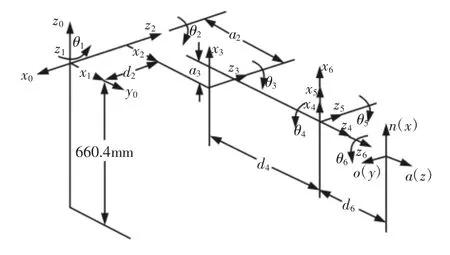
图1 PUMA560 机械臂模型Fig.1 PUMA560 Manipulator Model

图中：x0y0z0坐标系—基坐标系；坐标x1y1z1～x6y6z6—转动关节坐标系。

坐标系i 与坐标系i-1 之间的转换关系可用4 个量实现：关节角θi、连杆偏移di、连杆扭角αi-1、连杆长度ai-1，以上4 个参数中di、αi-1、ai-1由机械臂结构和尺寸确定，关节角θi为变量，表示机械臂的活动范围和活动能力。PUMA560 机械臂参数，如表1 所示。

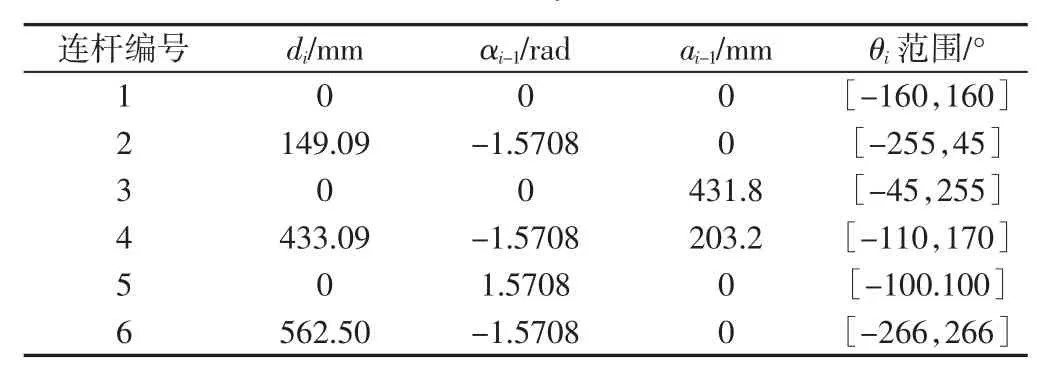
表1 PUMA560 机械臂参数Tab.1 PUMA560 Manipulator Parameters

2.2 改进的牛顿-欧拉动力学模型

对于n 连杆机械臂，使用牛顿-欧拉法得其动力学方程为：

式中：τ=（τ1，L，τn）—各关节驱动力矩；D（q）—n×n 惯性力矩；q—关节角位置；C（q，q˙）—科氏力和离心力之和；G（q）—重力项。

参考文献[7]，使用改进的牛顿-欧拉方程可以将驱动力转化为关于惯性参数的函数，为：

式中：Φ—n×10n 观测矩阵，仅与关节运动数据有关，p=（p1，p2，L pn）T—惯性参数矩阵；pi—第i 个连杆的惯性参数向量，即：

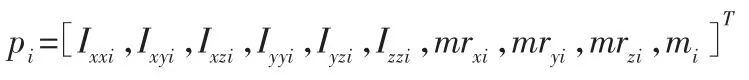
式中：Ixxi，Iyyi，Izzi—相对于连杆i 质心坐标系的三维质量惯性矩；Ixyi、Ixzi、Iyzi—相对于连杆质心坐标系的三维质量惯性积；mi—连杆i 质量；mr—一阶质量矩。

在此需要强调的是，式（2）中未考虑关节的摩擦力矩，而关节的摩擦是复杂非线性现象，难以进行精确建模。最常用的摩擦力矩为线性摩擦模型：

式中：τf—各关节的摩擦力矩矩阵；sign（）—符号函数；fe，fv—库伦摩擦系数和粘性摩擦系数。

融合式（2）与式（3），得到考虑关节摩擦的动力学模型为：

式中：Φdyn—n×12n 观测矩阵；pdyn—考虑摩擦的动力学参数向量，

即：

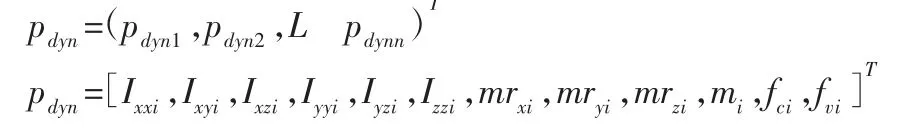
pdyn即为考虑摩擦情况下的待辨识动力学参数向量。

2.3 参数辨识优化模型

根据式（4），每给出一组动力学参数向量估计值p^dyn，则依据采集的关节角位置、关节角速度、关节角加速度可以反算出此时的驱动力矩τm。当驱动力矩实际值τ 与反算值τm间误差最小时，对应的动力学参数估计值即为最优辨识结果。

根据以上分析，设计动力学参数辨识的优化模型（目标函数）为：

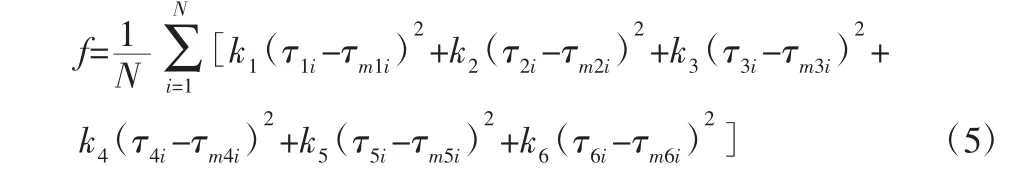
式中：N—样本数据长度；k1～k6—［0，1］间权重系数；τ1i～τ6i—6 个关节的实际驱动力矩；τm1i～τm6i—6 个关节的力矩反算值。

2.4 最优激励设计

在式（4）中，观测矩阵Φdyn一般为不满秩矩阵，这是因为有些动力学参数对动力学模型没有影响。另外，参数的可辨识性与激励轨迹密切相关，必须设计合适的轨迹激励，来激励整个机械臂系统，达到提高可辨识性与辨识精度的目的。最优激励轨迹为有限项傅里叶级数[8]，此时关节轨迹表达式为：

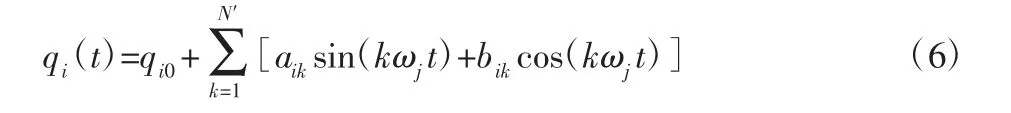
式中：qi0—关节角位置偏移量；N′—傅里叶级数谐波数量；ωj—基频；aik、bjk—正弦幅度和余弦幅度；t—时间。式（6）中的参数需要通过反复实验确定。

3 多变异策略花授粉算法

根据第2 节的分析和模型建立，将机械臂动力学参数辨识问题转化为以式（5）为目标函数的优化问题，本节提出了基于定向变异与均匀变异的改进花授粉算法对优化问题进行求解。

3.1 花授粉算法

花授粉算法是模拟花粉的自花授粉和异花授粉过程提出的[9]。自花授粉的传播范围较小，类似于寻优算法的局部搜索；异花授粉的传播范围较大，类似于寻优算法的全局搜索。花授粉算法核心思想为：设置一个转换概率p 和随机数rand∈（0，1），当rand＞p则进行全局搜索，若rand≤p 则进行局部搜索。算法核心内容包括以下4 个方面。

（1）全局搜索。全局搜索模拟Levy 飞行方式进行位置更新，方法为：

（4）算法结束条件。当所有花粉完成一次迭代时进入下一轮迭代，当迭代次数达到最大迭代次数Tmax时算法停止，输出全局最优即为花粉最优位置。

3.2 基于多变异策略的花授粉算法

3.2.1 融入随机机制的定向变异策略

使用随机机制将定向进化策略与传统局部搜索方式进行融合，设置一个随机数w，当rand＜w，则使用定向变异策略，当rand≤w，则使用传统局部搜索方法。将w 设置为黄金比例系数。

3.2.2 均匀变异策略

3.3 多变异策略花授粉算法流程

将定向变异策略和均匀变异策略融入到花授粉算法中，得到多变异策略花授粉算法流程，如图2 所示。

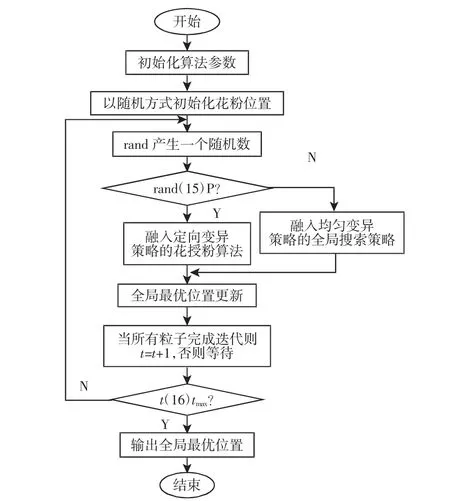
图2 多变异策略花授粉算法流程Fig.2 Flow of Multiple Mutation Strategies Flower Pollination Algorithm

4 实验验证及分析

4.1 判断指标

在实验前首先给出参数辨识的优劣评判标准。一是辨识的相对误差，由于PUMA560 机械臂的动力学参数已知，因此可以使用辨识值与真实值的相对误差进行判断。二是使用真实力矩序列与反算力矩序列的相关系数进行判断，两个序列的相关系数越接近于1，说明两个序列的相似性越高，则辨识结果越精确；两序列的相关系数越接近于0，说明两个序列相似性越差，则辨识结果精度越差。实际力矩｛τi｝与反算力矩序列｛τmi｝的相关系数为：

4.2 实验方案及数据获取

PUMA560 机械臂具有6 个转动关节，每个转动关节具有12个动力学参数，共有72 个参数待辨识。为了减小参数辨识规模，采取分批次辨识方法，首先将后3 个关节锁死，通过实验对前3个关节的动力学参数进行辨识；而后将前3 个关节锁死，使用实验对后3 个关节的动力学参数进行辨识。在此以前3 个关节的动力学参数辨识为例进行说明。

最优激励使用的傅里叶基频为ω=0.05Hz，由5 项傅里叶级数组成，3 个关节的最优激励轨迹，如图3 所示。为了减小测量误差，将总测试时间设置为60s，相当于3 个周期的激励函数，每次实验时重复跟踪最优激励，当机械臂瞬态效应消失后采集关节角数据，共采集300 组数据。

图3 最优激励轨迹Fig.3 Optimal Incentive Trajectory

关节的驱动力矩通过采集力矩电机的电流获得，通过力矩与电流的转换关系τ=KI 得到驱动力矩，其中τ 为驱动力矩，I 为电机电流，K 为比例系数。采集到的3 个关节驱动力矩，如图4 所示。

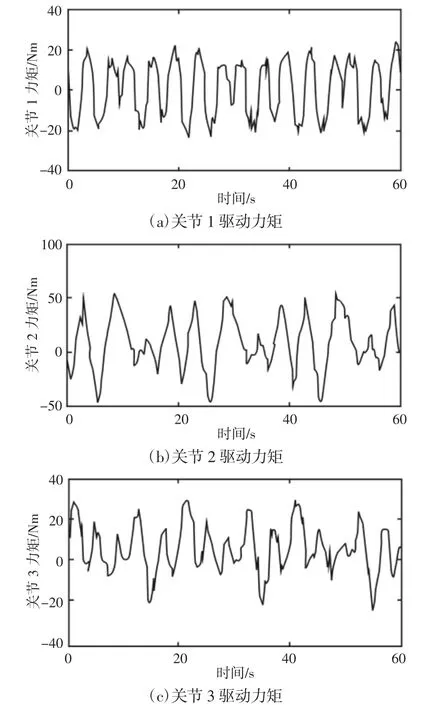
图4 关节驱动力矩Fig.4 Joint Driving Moment

4.3 实验结果及分析

使用多变异策略花授粉算法与花授粉算法同时对式（5）给出的优化问题进行求解，算法参数设置为：转换概率p=0.8，种群规模为40，花粉维度为36，最大迭代次数设置为100。为了避免随机性影响，两种算法各自独立运行20 次，选取20 次的最优解迭代过程进行展示，结果如图5 所示。从图5 可以看出，多变异策略花授粉算法迭代至30 次时搜索到全局最优解，传统花授粉算法迭代至35 次时陷入局部最优，目标函数值不再下降。从解的质量看，多变异策略花授粉算法搜索的最优解质量明显优于传统花授粉算法。这是因为算法后期传统花授粉算法的进化能力较差，陷入局部最优后没有跳出手段，加入定向变异策略和均匀变异策略后，不仅能够使花授粉算法跳出局部最优，而且在跳出后能够朝更优方向进化。为了进一步说明两种算法对动力学参数的辨识精度，选择部分动力学参数进行展示，结果如表2 所示。

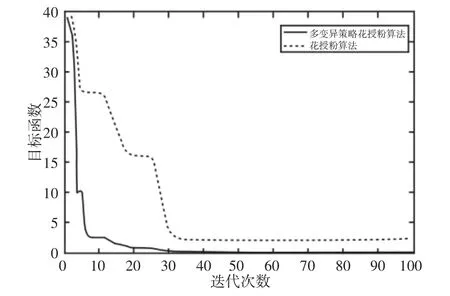
图5 最优解迭代过程Fig.5 Optimal Solution Iteration Process

从表2 中辨识结果可以看出，多变异策略花授粉算法的辨识相对误差远小于花授粉算法，有些相对误差甚至相差一个数量级。使用两种算法的最优辨识结果反算驱动力矩序列，计算驱动反算值与实际值之间的相关系数，结果如表3 所示。由表3 可知，使用多变异策略花授粉算法得到的参数最优值反算的力矩序列，与真实力矩序列的相关系数更大，说明此力矩反算序列与真实序列更相似，进一步说明改进花授粉算法搜索的动力学参数精度更高。综合表2 和表3，从辨识精度和力矩序列相关性两个角度，均说明了多变异策略花授粉算法对动力学参数的辨识结果更优。这是因为多变异策略不仅可以使算法有效跳出局部最优，而且在跳出后可以朝着最优方向进化，最终搜索到全局最优解。综合以上分析，多变异策略花授粉算法可以有效辨识出机械臂的动力学参数。

表2 部分动力学参数辨识结果Tab.2 Some Dynamic Parameters Identification Result

表3 力矩反算值与真实值相关系数Tab.3 Correlation Coefficient of Moment Identification Value and Real Value

5 结论

针对机械臂动力学参数的辨识问题，在实验的基础上，以驱动力矩实际序列与反算序列误差最小为评价标准，提出了多变异策略花授粉算法搜索参数最优值，经过验证得出了以下结论：（1）多变异策略可以使花授粉算法跳出局部最优，并在跳出后向全局最优进化；（2）多变异搜索策略辨识出的动力学参数相对误差小于传统花授粉算法。