结合频谱聚类与经验小波的轴承故障诊断方法

唐泽娴，林建辉，张 兵，杨基宏

（1.西南交通大学牵引动力国家重点实验室，四川 成都 610031；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266111）

1 引言

高速列车在交通与工业领域起到越来越重要的作用。作为传动装置中的核心部件之一，列车轴承工作环境复杂，发生故障的概率高，极大地威胁了列车的运行安全。为了保障乘客的生命安全并减少经济损失，对轴承的健康状况跟踪和故障识别是十分必要的。

振动分析具有经济、实用的优点，是故障诊断领域中最为广泛运用的方法之一。当轴承表面出现局部损伤后，轴承运行时损伤点会和与之接触的元件表面撞击，产生一系列的高频振动，即共振，并受轴承故障频率的幅值调制。为了挖掘故障信息，包络解调技术常被运用于高频共振信号的分析，而合理的共振带选取直接影响解调效果。迄今为止，许多研究学者在这方面取得丰硕的研究成果[1-3]，其中，基于频带划分的滤波方法被广泛研究和使用：小波包分解基于小波滤波器组对频带进行树状二分[4]，快速谱峭度算法通过短时傅里叶进行频带细分和局部谱峭度的计算筛选出目标频带[5]。但是，小波包分解和快速谱峭度算法的频带分解宽度是固定的，对共振带的选取缺乏自适应性。

由Gilles 提出了经验小波变换（Empirical Wavelet Transform，EWT）[6]，该算法同时具备了小波变换的快速运算特性和经验模态分解（Empirical Mode Decomposition，EMD）的自适应性。该算法利用小波滤波器组滤波的框架实现特定频带滤波。针对滤波频带边界，Gilles 提出基于频谱极值分布和尺度空间两种方法进行滤波频带划分。

极值点分布简洁易操作，但是当频谱分布较为杂乱，没有明显中心频率时，该方法的频带边界确定能力受限。尺度空间法运算量大，倾向于将频谱划分过细。除此以外，其他学者还研究了基于稀疏指引[7]和泊松相关系数[8]等理论的频带划分方法，而这些方法需要足够的先验信息才能较好地划分频带。

根据轴承引起的高频共振带在频谱上具有丛簇分布特点，将频谱中的“突出值”，即幅值较为明显的部分挖掘出来（区别于背景噪声成分），根据聚类法分割这些点，认为聚集成簇的点集处于同一共振带。

当出现复合故障时，不同的故障信息可存在于同一个频段当中，但若幅值存在差异，则可根据幅值进行阈值降噪后再进行包络解调，可以突出不同类型的故障信息。

2 算法原理

2.1 经验小波变换

经验小波变换基于选取合适的傅里叶谱支撑集建立小波滤波器组。假设频带［0，π］可以被分割成N 个连续的代表不同振动模态的区间，对于给定的信号，应能找到对应的N 值。每个区间记为：Λn=［ωn-1，ωn］，且∪¨ Λn=［0，π］。

经验小波被定义为在每个Λn上是一个带通滤波器。目前经验小波函数是通过调用Meyer 小波来实现的[1]。对所任意n＞0，n∈Z，经验尺度函数和经验小波依据角频率ω 和β（·）函数有如下定义：

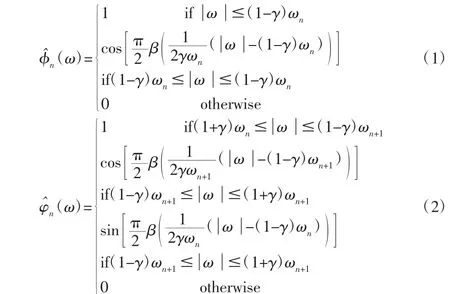
2.2 箱型法“突出值”选取

2.3 凝聚层次法聚类

采用自下而上的方法，首先将每个数据点作为单独的类，然后根据设定的规则不断地融合相近的类，直到所有对象都合并为一个聚类或满足一定条件，“突出值”的选取减少了凝聚层次聚类的运算复杂度且使各聚类分布特征更加明显。采用欧式距离来衡量数据点（集）和数据点（集）间的相似性。

（x1，y1），（x2，y2）是数据点或者数据集质心坐标。数据点（数据集）与距离最近的数据点（数据集）合成新的聚类。。 ，

2.4 平方包络及相关系数

文献[10]指出局部故障信号故障并不是真正的周期函数，但是，如果信号偏离周期信满足在一定范围内即可视为周期函数。为了使信号更接近周期信号，抑制非周期成分，对原信号进行平方包络分析，突出信号中的幅值较大成分（常出现在冲击发生处）。

相关系数可用于表征两个信号在一段时间内的相似程度，定义互相关系数计算为：

由层次聚类分析原理可知，每增加一个聚类项，原聚类中某一数据集被一分为二。计算新增数据集对应的信号包络平方互相关系数，若相邻自信号间的互相关系数大于0.2 则信号且较为相似，可归于同一共振带中。

2.5 Teager 能量算子

能量算子是一种非线性差分算子，能够缩短运算时间强化瞬态特征，但是在强噪的情况下效果并不是很好[11]，而经验小波滤波后的信号抑制了部分噪声和无关信号，提高信号的信噪比。Teager 能量算子能抑制端点效应进行时频表示，则经Teager 能量算子运算后得到瞬时能量信号φ｛x（t）｝：

式中：x˙（t）、x¨（t）—信号对时间的导数。对平方包络的求取和目标信号的解调均采用Teager 能量算子。

2.6 算法步骤

（1）获取信号频谱图，利用箱型图法识别频谱中的“突出值”。

（2）对“突出值”进行凝聚层次聚类。

（3）自顶向下，从聚类为2 开始，根据聚类确定频带边界进行滤波，求取相邻频带信号平方包络的互相关性，若出现互相关系数大于0.2，返回上层聚类结果，否则继续执行。

（4）平方包络峭度值较大分量进行自相关能量算子解调分析。

2.7 动态阈值

若存在复合故障时，不同故障的共振带可能相同而不易区分，但由于故障形式和程度的不同，共振幅值存在区别，可通过动态阈值法进行划分[12]。

动态阈值的计算公式为：

式中：l—滑动平均的窗宽。即滑动窗口，求取窗口中对应数据的平均值最为该窗口对应阈值，形成动态阈值曲线。

通过提取大于（小于）阈值的平方包络部分，将小于（大于）阈值的点置0，而后分别解调，突出不同故障类型的频率。

3 实测数据验证

为测试算法的有效性，使用高速列车轮对振动台实测数据进行分析。试验台布置，如图1 所示。由一个电机、驱动轮对、加载装置、测试轮对和轴箱组成。试验采用ZW9609A-18 SN7068 型三向应变式传感器进行检测。测取垂、横、纵三个方向的振动加速度数据，以垂向振动数据进行后续研究说明，该方向传感器灵敏度为97.6mv/g，振动信号的采样频率为10kHz。外圈及滚子故障设置示意图，对滚子、外圈单一故障及复合故障轴承在100km/h工况试验测试，通过IMC 数据采集器采集信号进行分析。其中，滚子相关参数，如表1 所示。

图1 轴承台架试验装置图Fig1 Diagram of Test Equipment for Bearing Pedestal

表1 滚子相关参数Tab.1 Parameters of Rollers

则在100km/h（转频为10.29Hz）工况下滚子和外圈故障频率分别为67.8Hz 和83.8Hz。

3.1 滚子故障

取1s 振动数据，其时域波形、频谱，如图2 所示。

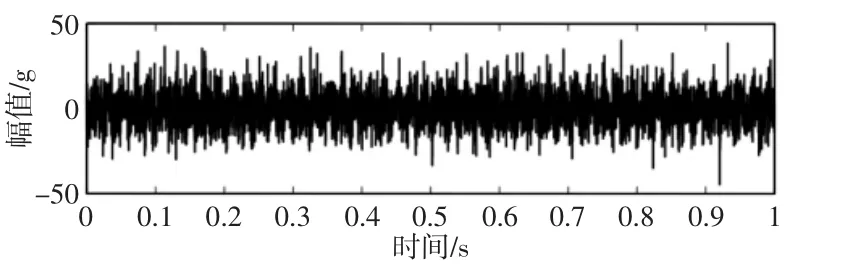
图2 振动信号时域图Fig.2 Vibration Signal in Time Domain

依照经验小波变换包中自带的频带边界确定函数（极大极小值法、尺度空间法）得到该频谱的分割结果，划分结果显示：由于共振带频谱幅值太小，极大极小值法幅值较大的低频成分分布影响，无法快速将共振频带提取出来，而过细划分低频频谱部分。尺度空间存在严重的频带划分过细问题，且算法运行时间较长。

依照1.6 算法流程，首先获取频谱中的“突出值”，利用层次聚类法聚类，得到聚类数为3、4 时的聚类结果，以聚类数为3 为例，如图3 所示。不同颜色的圆圈代表不同聚类数据集，虚线为对应的频率边界线。

图3 频带划分：频带数为4Fig.3 Frequency Band Division with Clustering Number 4

根据上述划分准则，当聚类数为3 时划分区间为：频带1［1Hz，1366Hz］，频带2［1366Hz，2833Hz］，频带3［2833Hz，5000Hz］。聚类数为4 划分区间为：频带1［1Hz，795Hz］，频带2［795Hz，1366Hz］，频带3［1360Hz，2833Hz］，频带4［2833Hz，5000Hz］。

后者对应相邻频带滤波信号的互相关数为：0.4315，0.0102，0.0981，说明频带1 与频带2 内的故障信息相似度较高，则返回聚类数为3 的频带划分结果。选取平方包络峭度值最大的频带3进行解调，其对应包络谱，如图4、图5 所示。从图中可以看出故障频率fBSF显著，其2 至5 倍频也可从包络谱中识别到，因此该算法可成功检测出滚子故障。

图4 平方包络图Fig.4 Diagram of Square Envelope

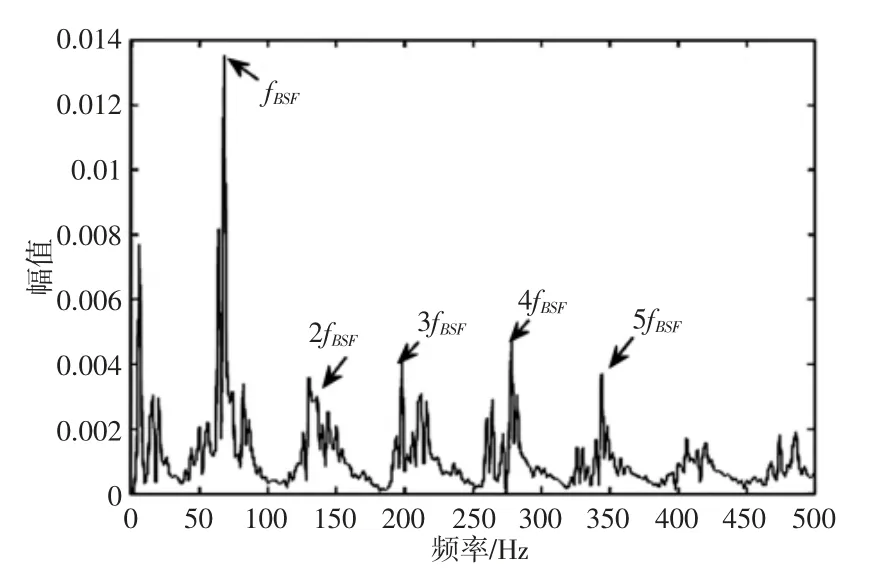
图5 平方包络解调结果Fig.5 Demodulation of Square Envelope

3.2 外圈故障

取1s 外圈故障轴承振动数据，得其时域波形、时域平方包络及频谱，如图6～图8 所示。通过1.6 所述算法，依照聚类结果进行子频带划分，聚类数为3 划分区间为：频带1［1Hz，1035.5Hz］，频带2［1035.5Hz，2373Hz］，频带3［2373Hz，5000Hz］。选取频带3滤波信号进行解调。滤波信号平方包络图，如图7 所示。平方包络解调结果，如图8 所示。

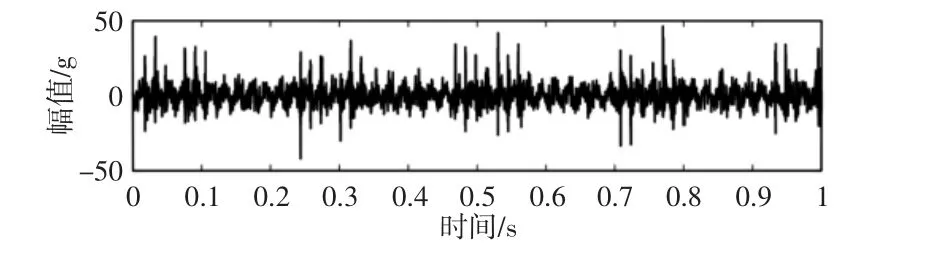
图6 振动信号时域图Fig.6 Vibration Signal in Time Domain

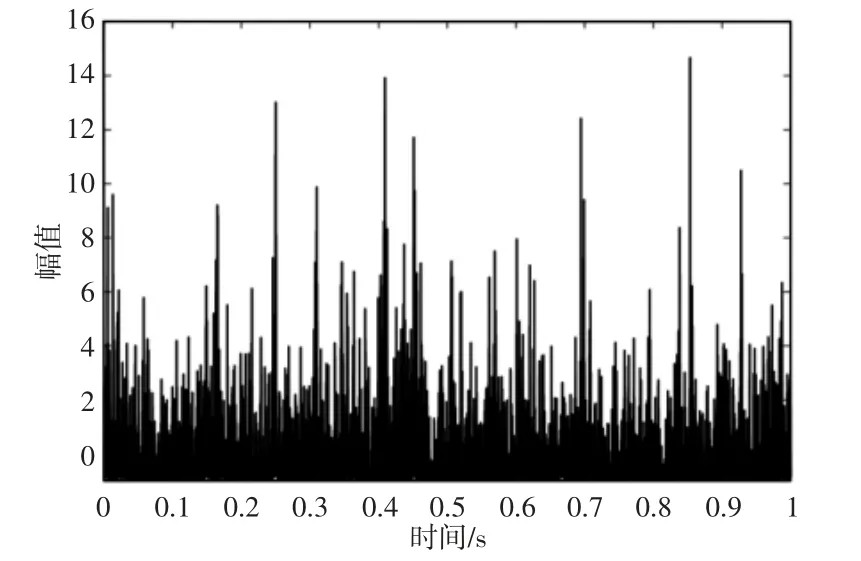
图7 平方包络图Fig.7 Diagram of Square Envelope

从图8中可以明显地发现外圈故障特征频率及其二倍频与三倍频，因此，所提方法可以有效地实现外圈故障的诊断。

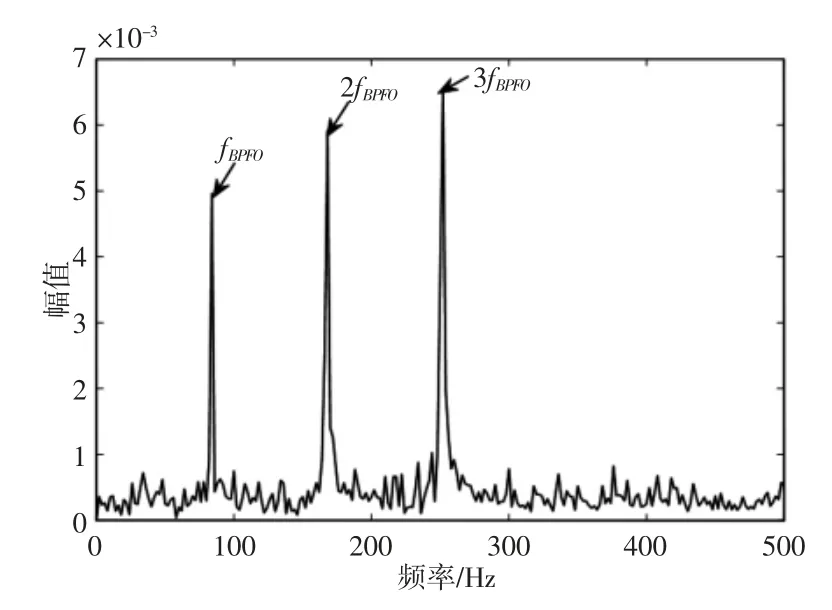
图8 平方包络解调结果Fig.8 Demodulation of Square Envelope

3.3 轴承滚子、外圈混合故障

轴承外圈和滚动体混合故障轴承振动时域图，如图9 所示。其频谱聚类结果为3，划分的频带为：频带1［1Hz，1135Hz］，频带2［1135Hz，2169Hz］，频带3［2169Hz，5000Hz］。阈值示意图，如图10 所示。选取频带2 滤波信号进行解调。当轴承包含混合故障时，不同故障引起的冲击均可在高频处引起共振，其共振区间可能发生重叠。但由于故障类型和严重程度的不同，不同故障激起的共振强度不同，由2.1 和2.2 的平方包络图可得，轴承滚子和外圈单一故障的时域分布存在明显的差异。

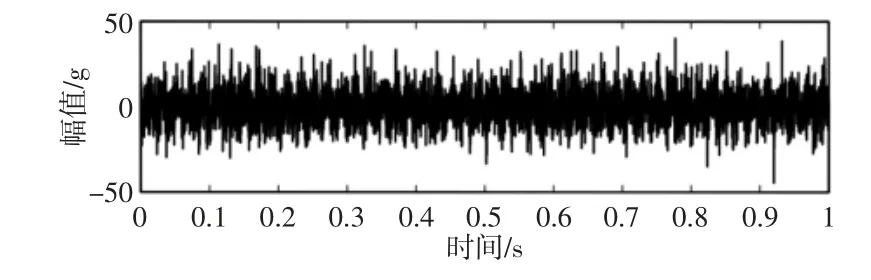
图9 振动信号频域图Fig.9 Vibration Signal in Frequent Domain

图10 阈值示意图Fig.10 Diagram of Threshold

图11 平方包络解调结果Fig.11 Demodulation of Square Envelope

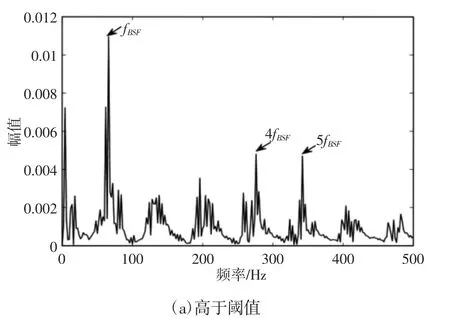
对比图11，图12 进行阈值划分的解调结果，能够识别出滚子和外圈的故障，说明前述算法在混合故障中的可行性，其中，滚子故障特征频率占主导。阈值划分后的分解结果，外圈故障的特征频率得到凸显。

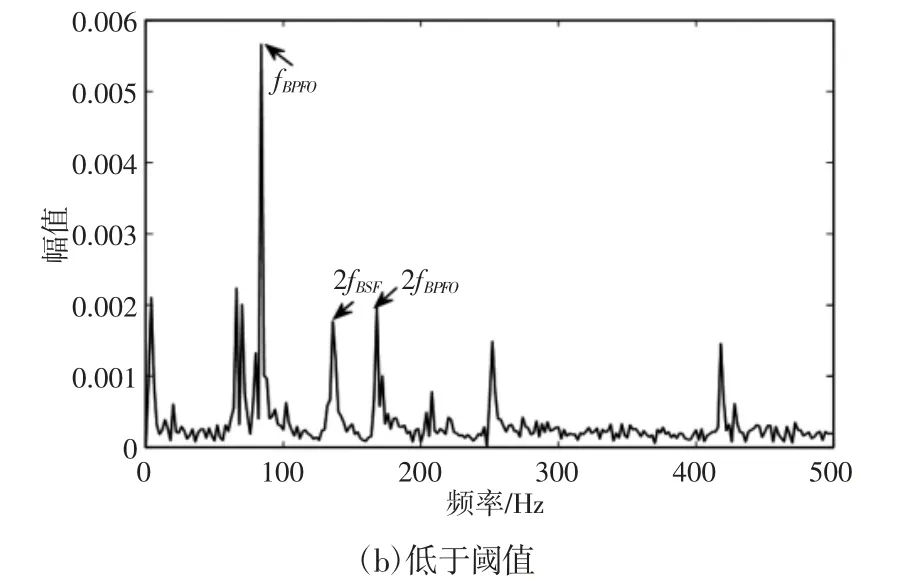
图12 动态阈值降噪后平方包络解调结果Fig.12 Demodulation of Square Envelope after Noise Reduction Using Dynamic Threshold

4 结论

通过频谱幅值显著数据点的分布特征进行频带划分，能够实现频谱的自适应共振带提取。通过对平方包络的分析，可以突出原信号中的冲击成分，平方包络的互相关系数判断能使故障信息较为一致的信号划分在同一频带当中。该方法相比于小波分解和快速峭度谱变换，充分利用了轴承故障共振的特征，具有带宽划分自适应的特点，且避免频带划分过细的现象。实测数据验证了该算法对工程数据的有效性，在轴承滚子、外圈的单一故障和复合故障试验中，均成功提取出故障频率及倍频成分。由于不同类型故障信号存在时域分布的差异，在信号的不同幅值区间，不同故障类型的能量占比有所区别，因而利用动态阈值法进行时域划分，将复合故障信号中不同的故障成分进行突出，便于识别。提出的方法具有信号自适应性，但该方法受频谱分布特征的影响显著，可以进一步优化其稳定性，并拓宽其适用范围。