微动接触中分形粗糙表面的接触应力研究

阮晓光，麻诗韵，李 玲，蔡安江

（西安建筑科技大学机电工程学院，陕西 西安 710055）

1 引言

微动广泛地发生于紧固配合的零部件之间，会引起部件的磨损和疲劳失效。影响微动的因素有很多，主要包括载荷形式、材料属性、润滑条件、环境温度以及接触面表面粗糙度[1]。这些因素主要是通过影响接触面的接触压力和剪切摩擦力分布进而引发结合面的微动损伤。

许多学者已经对各种微动接触下结合面的微动行为进行了研究，得到了很多有价值的结论[2-3]。但大多数文献所采用的模型都是光滑接触表面，忽略了表面粗糙度对微动行为的影响。部分学者实验研究了表面粗糙度对摩擦行为的影响[4-5]。文献[4]通过平面接触的扭转微动磨损装置在不同的表面粗糙度和纹理方向下检测摩擦力矩，结果表明摩擦力矩和累积耗散能量随着表面粗糙度的增加而增加。考虑结合面的表面粗糙度时，结合面接触区域离散化，采用实验的方法很难对接触区域内每一点的接触应力进行测量。随着计算机运算速度的提高，有限元仿真技术取得了长足的发展。一部分学者采用有限元方法分析表面粗糙度对摩擦行为的影响[6-7]。文献[7]提出了一种多尺度方法来研究微动磨损中的粗糙度效应。结果表明在完全滑移条件下粗糙度对微动磨损的影响较小。

建立包含粗糙表面的接触模型的关键在于如何表征粗糙表面。通常用于描述表面粗糙度的方法大都依赖于粗糙表面的统计参数，而这些统计参数受样本大小的影响，不能够准确地反映粗糙表面的全部特征。而利用分形理论模拟的分形表面具有连续性，不可分性，尺度不变性和自亲和性的特征[8-9]，克服了表面粗糙度表征对样本大小的依赖，对粗糙表面的描述更稳定、更精确。因此，一些学者利用分形表面模拟粗糙表面来研究结合面的接触特性[10-13]。文献[11]基于分形理论建立了刚性光滑平面与粗糙平面三维接触模型，获得外加载荷与结合面变形之间的函数表达式。文献[12]以分形理论为基础，推导了考虑表面微凸体相互作用影响的结合面接触刚度分形模型。

这里的目的在于研究微动接触中接触面的表面粗糙度对接触压力和剪切摩擦力分布的影响，同时讨论了材料的弹性、弹-塑性和载荷幅值对剪切摩擦力的影响。为了达到这个目的，编写Python 脚本将Matlab 中利用Weierstrass-Mandelbrot 函数（W-M函数）构造的分形曲线的轮廓坐标数据导入ABAQUS，并使用样条曲线拟合轮廓坐标，从而构建包含粗糙表面的二维柱面/平面接触模型，进行有限元仿真。

2 二维粗糙表面的表征

分形理论模拟的粗糙表面的二维（2-D）表面轮廓高度由WM 函数给出[14]。

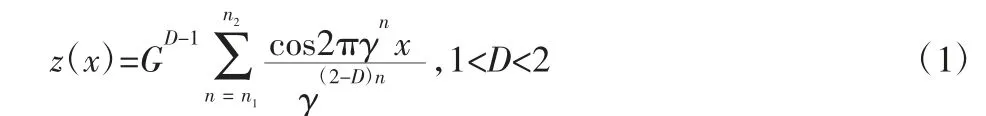
式中：z（x）—分形表面轮廓高度；x—轮廓的位置坐标；G—特征尺度系数；D—分形维数；γn—轮廓的空间频率，γ—常数，通常取γ=1.5 较适于表面轮廓特征；轮廓结构的最低频率与粗糙度样本长度关系为γn1≈1/L1；n1—W-M 函数的初始项；L1—粗糙度样本取样长度。

根据式（1）的函数，当G=0.01nm，L=1mm，γ=1.5，n1=5，n2=70时，取不同的分形维数D，在Matlab 中分别绘制二维表面轮廓，如图1 所示。图1 中的二维粗糙表面分形曲线，能够反映粗糙表面的微观形貌。图1 表明，随着分形维数D 的增大，曲线波动趋于一致，表现出自相似性，处处连续但不可导；表面轮廓的峰值和谷值变小，表面愈加光滑，粗糙度减小。根据式（1）的函数，当D=1.35，L=0.3mm，γ=1.5，n1=5，n2=70 时，分别取不同的特征尺度系数G，仿真生成二维表面形貌，如图2 所示。L 取0.3mm 是为了清晰地观察图中分形曲线轮廓特征。图2 表明，随着特征尺度系数G的不断增大，图像波动形式一致，但表面峰值和谷值逐渐增大，表面轮廓愈加粗糙，粗糙度增大。

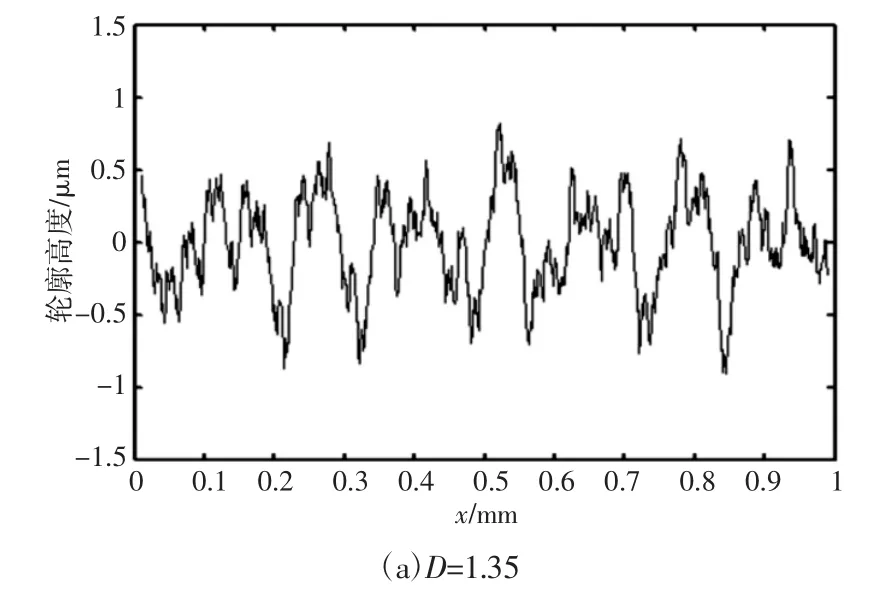
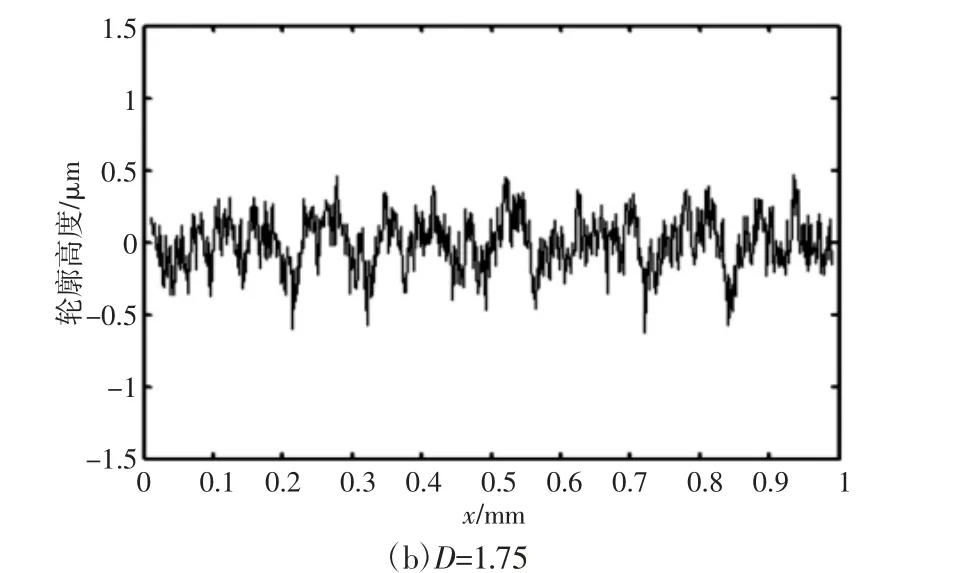
图1 不同分形维数下的分形曲线Fig.1 Fractal Curves Under Different Fractal Dimensions

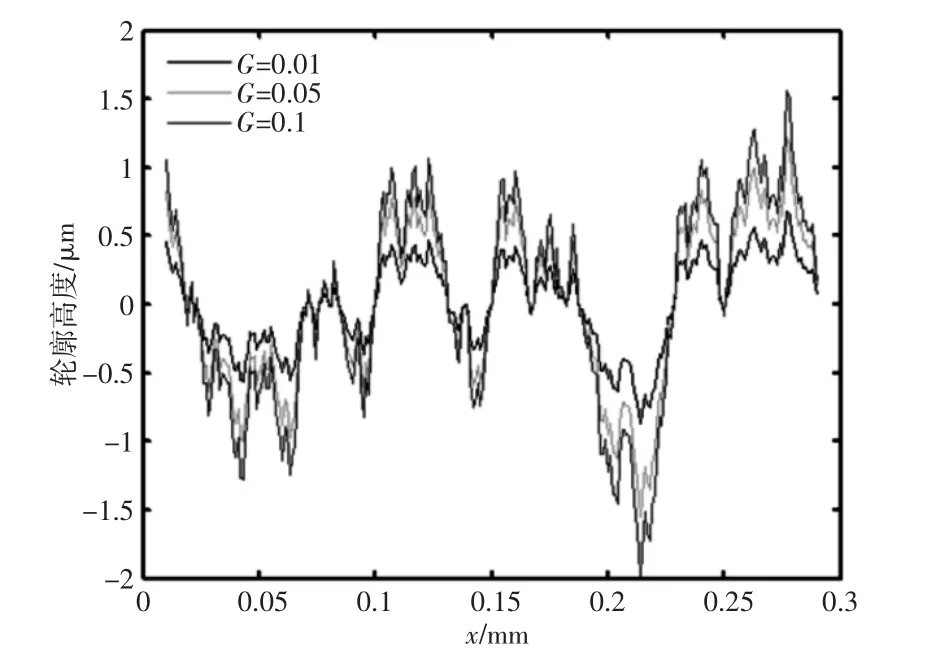
图2 不同特征尺度系数下的分形曲线Fig.2 Fractal Curves Under Different Characteristic Scale Factors

3 仿真分析

3.1 有限元模型

基于微动实验模型建立二维柱面/平面接触有限元模型，如图3 所示。在圆柱试件的顶面施加均布的法向载荷P，并通过多点约束选项（MPC）在顶面中心点施加切向位移载荷S。下试件两侧约束水平方向位移，底部约束竖直方向位移。

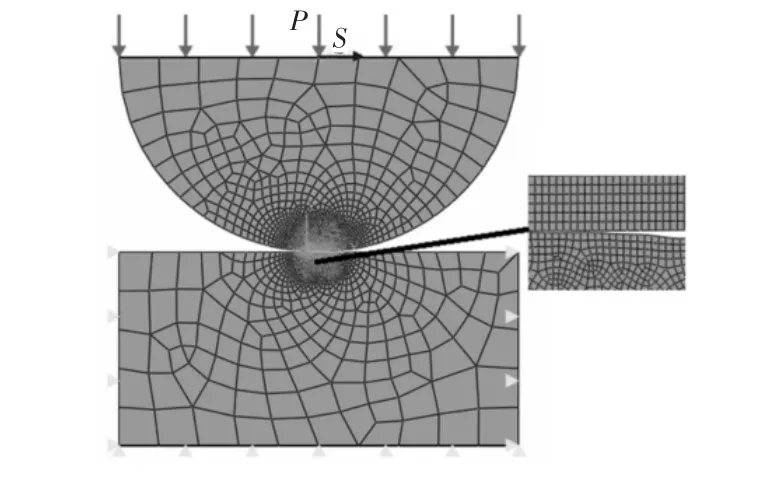
图3 有限元模型Fig.3 Finite Element Model

对有限元模型的接触面进行接触属性设置，法向定义为硬接触；切向定义为具有各向同性摩擦的库仑摩擦，摩擦系数为0.6。为了获得更加准确的接触参数，采用有限滑移算法，并将切向约束定义为拉格朗日乘数法。在有限元模型中，采用主-从面的设置定义两个接触面，主面为圆柱试件的下表面，从面为下试件的上表面。这种设置便于提取接触区域的接触变量。圆柱试件的半径为5mm，下试件的长宽分别为10mm 和5mm。为了更加深入地研究表面粗糙度对结合面接触应力的影响，分别建立了光滑表面接触模型和考虑粗糙表面的接触模型。当建立考虑粗糙表面的接触模型时，创建Python 脚本将Matlab 中利用W-M 函数构造的分形曲线的轮廓坐标数据导入ABAQUS，并使用样条曲线拟合轮廓坐标，从而在下试件顶面中心区域引入长度为0.6mm 的分形曲线来模拟粗糙表面。有限元模型的网格类型为四节点平面应变单元（CPE4），并对模型接触区域附近的网格进行细化处理。光滑接触模型网格细化后的单元尺寸为（5×5）μm，粗糙表面接触模型细化后的网格单元为（1×1）μm。一次仿真分析具体的加载历程，如图4 所示。其包括两个分析步，法向载荷P 在分析步1 施加，并在分析步2 中保持恒定施加，切向位移载荷S 在分析步2 施加，并在分析步结尾达到最大值。

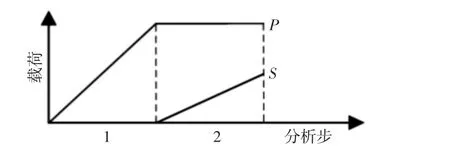
图4 加载历程Fig.4 Loading History

3.2 材料属性

为了研究不同接触材料和材料属性对粗糙表面接触模型接触应力分布的影响，考虑了steel 和Al 两种材料，并分别模拟了完全弹性和弹-塑性两种情况，上下试件采用同种材料。两种材料的力学属性，如表1 所示。两种材料的真实应力和塑性应变的关系曲线，如图5 所示。

表1 材料属性Tab.1 Material Properties

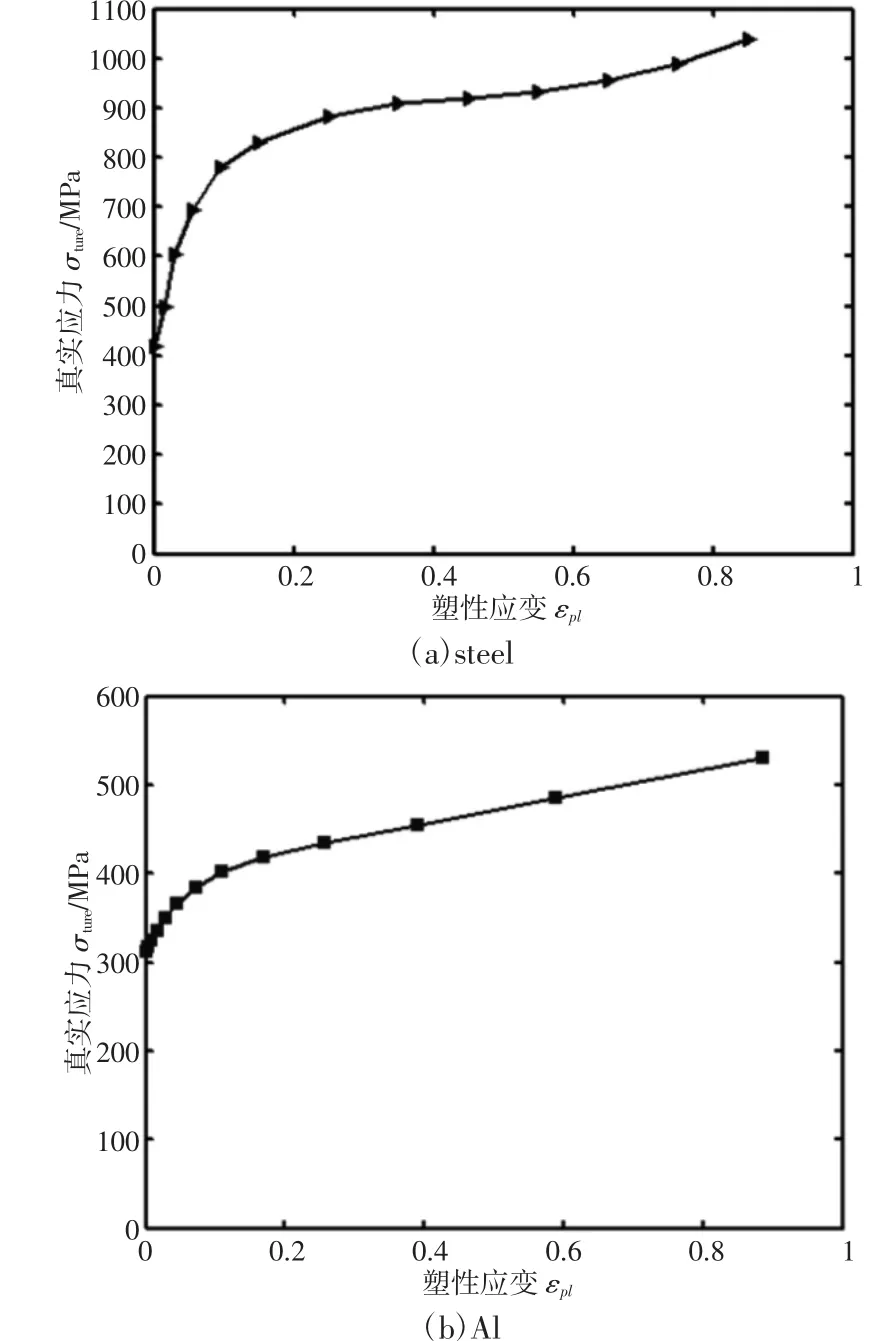
图5 真实应力和塑性应变的关系曲线Fig.5 The Relationship Curve of Between True Stress and Plastic Strain

4 结果与讨论

4.1 不同条件下的增量步数

当模型的材料属性和载荷条件不同时，求解模型所需的增量步数也会发生改变。表2 给出了各种不同条件下，求解一次仿真所需的增量步数。表中1 代表求解分析步1 所需的增量步数，2代表分析步2 所需增量步数。从表2 可以看出，考虑材料弹-塑性（E-P）时，分析步1 所需增量步数明显增大。当材料属性为完全弹性（E）时，分析步2 所需增量步数不随切向位移幅值发生改变，而考虑材料弹-塑性时，分析步2 所需增量步数随着位移载荷的增大而增大。这是因为考虑材料弹-塑性时，由于塑性变形的存在，试件发生变形的区域会增大，计算的收敛速率减小，导致增量步数增加。

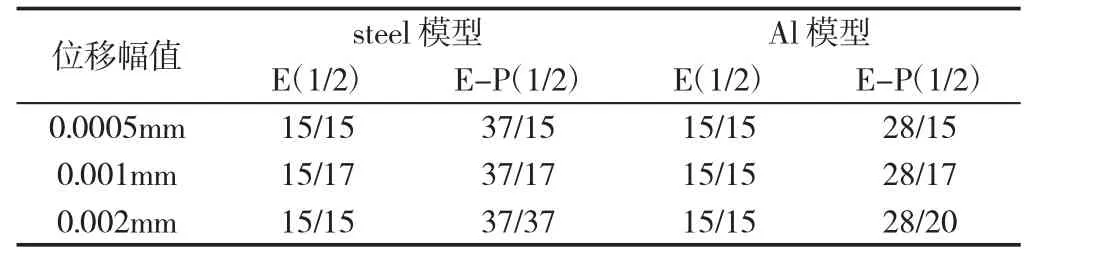
表2 不同条件下的增量步数Tab.2 Number of Incremental Steps Under Different Conditions

此外，还观察到当材料为完全弹性时，求解一次仿真两种材料所需的增量步数基本相同，而考虑材料弹-塑性时，steel 模型所需的增量步数明显多于Al 模型所需的增量步数。这是因为相同载荷条件下，steel 模型的接触压力值较大，steel 模型率先产生塑性变形，收敛速率减小，因而所需的增量步数更多。

4.2 表面粗糙度对接触压力的影响

当法向载荷相同时，分别讨论光滑接触模型和粗糙接触模型的接触压力分布。光滑接触模型，外部法向载荷为20MPa 时，模型的接触压力分布，如图6（a）所示。当下试件接触区域轮廓为D=1.35 的分形曲线，法向载荷为20MPa 时，模型的接触压力分布，如图6（b）所示。从图中可以看出当接触表面光滑时，接触区域均匀接触，当接触区域为粗糙表面时，接触发生在个别凸起的表面峰上。注意到，由于粗糙表面接触中法向载荷被个别凸起的表面峰承担，导致局部应力集中。因此，图6（b）中的最大应力值远大于图6（a）中的应力最大值。为了进一步研究表面粗糙度对接触表面接触压力分布的影响，对不同粗糙度接触表面的接触压力分布进行了研究，如图7 所示。根据图1 所述，通过改变分形维数来获得不同粗糙度的接触表面。下试件接触表面较为光滑时的接触压力分布，如图7（a）所示。下试件接触区相对粗糙时的接触压力分布，如图7（b）所示。图7（a）和图7（b）所对应接触模型的外部载荷和约束条件均相同。从图7 可以看出，粗糙表面的存在导致接触压力分布为非光滑曲线，局部应力集中程度高。当表面粗糙度较大时，结合面上接触压力的分布是离散的。这是因为当接触表面粗糙度较小时整个接触表面完全接触，但由于接触表面凹凸不平引起接触表面各个接触点的变形量各不相同，从而导致整个接触面上接触压力分布连续而不光滑以及局部应力集中。当表面粗糙度较大时，相同的法向载荷作用下，整个接触区域只有个别凸起的表面峰发生接触，从而引起接触压力分布离散化，并且局部应力集中严重，具体表现为个别接触点的应力值非常大。

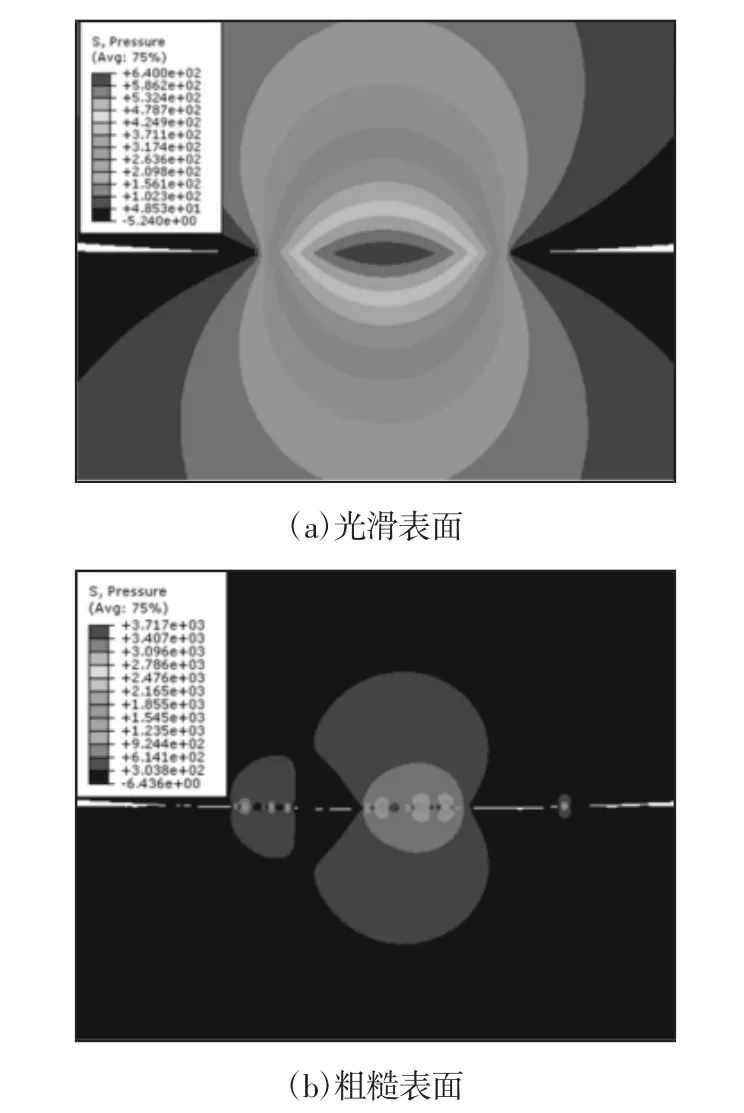
图6 接触区域的压力分布（P=20MPa）Fig.6 Pressure Distribution in Contact Area（P=20MPa）

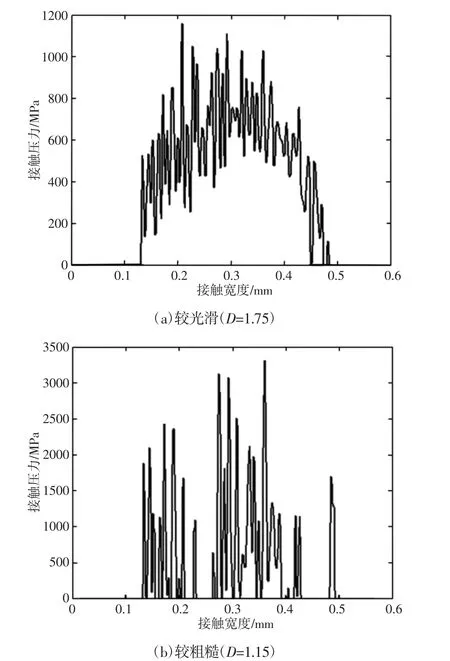
图7 不同表面粗糙度下的接触压力分布Fig.7 Contact Pressure Distribution Under Different Surface Roughness

4.3 不同条件下的剪切摩擦力分布

接触面的剪切摩擦力分布直接影响接触面的磨损形貌和微动裂纹的初始位置，同时其影响因素众多。为了尽可能全面地研究粗糙表面接触模型的剪切摩擦力分布形式，仿真分析了不同接触副材料、不同材料属性、切向载荷幅值以及法向载荷幅值对切向剪切摩擦力分布的影响规律。

当法向载荷为P=20MPa，切向位移载荷为S=1μm，接触副材料为steel 时，分别考虑完全弹性和弹-塑性时的剪切摩擦力分布，如图8 所示。接触副材料为Al 时分别考虑完全弹性和弹-塑性时的剪切摩擦力分布，如图9 所示。图中虚线和实线分别代表粗糙接触模型和光滑接触模型。从图8、图9 可以看出，当接触副材料为完全弹性时，相比于光滑接触模型，粗糙接触接触模型的接触区域边缘存在很大的应力集中，而考虑材料弹-塑性时，接触区域边缘的应力集中要小的多。这是因为考虑材料塑性时，相同法向载荷下接触区域宽度明显增加，而相应的接触压力值比材料完全弹性时小且波动幅度减小。

从图8 和图9 的对比不难发现，在相同的载荷条件下，弹性模量较小的Al 分别考虑完全弹性和弹-塑性时，接触区域的剪切摩擦力波动很小，而弹性模量较大的steel 考虑材料弹-塑性时，接触区域剪切摩擦力剧烈波动。法向载荷一定，接触副材料为Al时，剪切摩擦力随切向位移幅值的变化曲线，如图10 所示。图10表明材料为完全弹性或考虑弹-塑性时，随着切向位移幅值的增大，剪切摩擦力都逐渐增大。此外，可以看出，材料完全弹性时接触边缘的剪切摩擦力大于考虑材料弹-塑性时接触区域边缘的剪切摩擦力。

图8 steel 不同材料属性时的剪切摩擦力分布Fig.8 Shear Force Distribution Under Different Material Properties of Steel

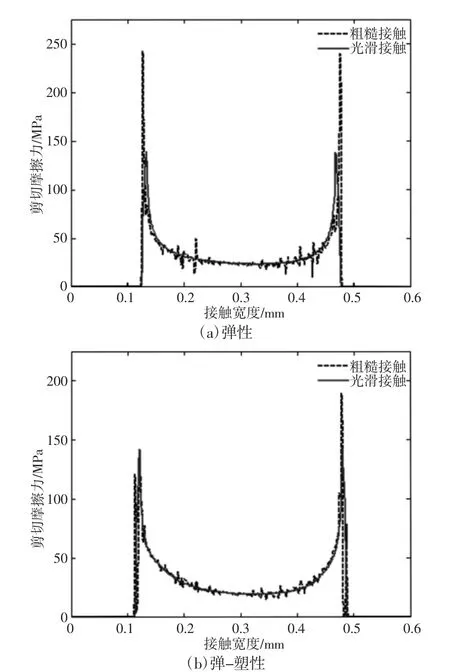
图9 Al 不同材料属性时的剪切摩擦力分布Fig.9 Shear Force Distribution Under Different Material Properties of Al

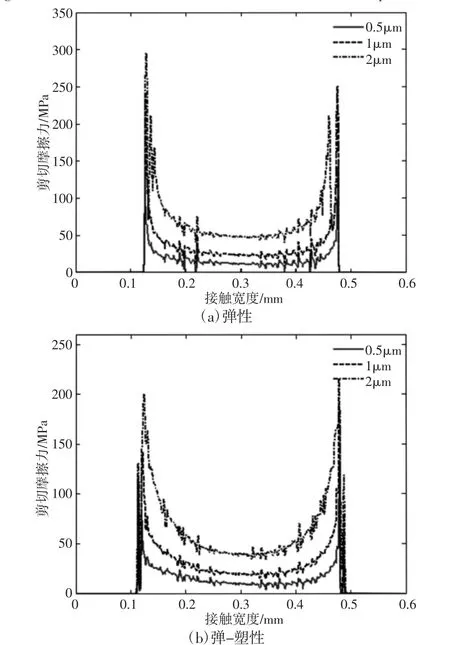
图10 不同切向位移载荷下的剪切摩擦力分布（法向载荷P=20MPa）Fig.10 Shear Force Distribution under Different Tangential Displacement Loads（Normal Load P=20MPa）

切向位移载荷一定，接触副材料为Al 时，剪切摩擦力随法向载荷幅值的变化曲线，如图11 所示。从图11 中可以看出，当材料为完全弹性或考虑弹-塑性时，随着法向载荷的增大，接触区域宽度明显增加，曲线分布形式变化不大。此外，从图11 还可以看出，相同法向载荷下，考虑材料弹-塑性形时，剪切摩擦力峰值较小，而接触区域较大。这是因为考虑材料塑性时接触压力峰值小，接触区域宽度较大，而接触压力是剪切摩擦力的决定因素之一。

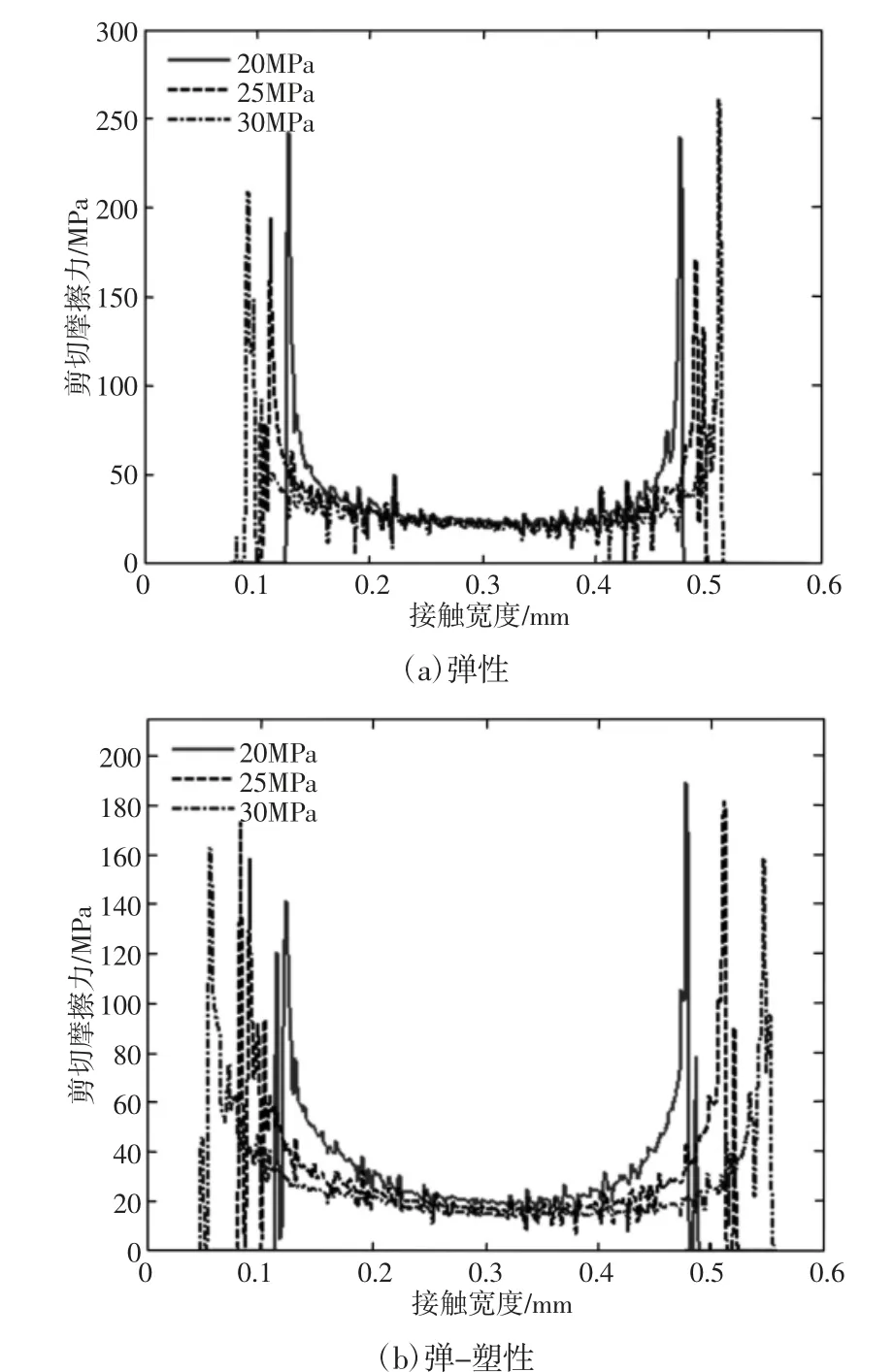
图11 不同法向载荷下的剪切摩擦力分布（位移载荷S=1μm）Fig.11 Shear Force Distribution Under Different Normal Loads（Displacement Load S=1μm）

5 结论

利用有限元方法研究了微动接触中分形粗糙表面的接触应力分布规律，可以得出以下几点：

（1）考虑材料弹-塑性时，接触模型的接触区域明显增大，仿真一次所需的增量步数也明显增大；当接触副的材料不同时，其仿真一次所需的增量步数差异明显。（2）接触模型中粗糙表面的引入，导致接触面上的接触压力分布为非光滑曲线，局部应力集中程度高；当表面粗糙度较大时，接触面上接触压力的分布会发生离散化。（3）在粗糙接触模型中，考虑材料弹-塑性时，不同接触副材料的剪切摩擦力沿粗糙表面的分布差异明显。