不同温升下受轴向载荷的球轴承内部接触热阻计算方法

张义民，王孟卓，李铁军

（沈阳化工大学装备可靠性研究所，辽宁 沈阳 110142）

1 引言

滚动轴承是旋转机械中关键的部件之一，目前在旋转机械中所面临的许多问题都是由于轴承的设计或应用不当造成的，因此，了解轴承的工作特性对于为特定的设计做出正确的选择是至关重要的[1]。深入研究滚动轴承的热特性有利于获得较为真实的轴承温度场分布情况和提高轴承的工作寿命[2-3]。轴承内部界面的不完全接触而形成的接触热阻对轴承的热流传导、温度场分布有较大的影响[4]。由于滚动轴承相对复杂的几何结构和力学特性，轴承内部接触热阻的精确解析建模存在许多难点。文献[5]建立的滚动轴承静力学模型和拟静力学模型、文献[5]先后建立的动力学模型都能够有效确定轴承在工作状态下的载荷、刚度矩阵、接触角度，这些都为轴承内部接触热阻的研究奠定了基础。国内外大量学者针对滚动轴承的接触热阻进行研究，取得了一系列进展。文献[6]提出了一种确定椭圆区域的接触热阻方法，这种方法可用于分析球形滚动体与滚道沟之间的接触热阻。文献[7]提出了一种可用于分析轴承内圈与轴、外圈与轴承座的接触热阻的方法。文献[8]应用上述两种方法对角接触球轴承的热阻网模型进行优化。针对受径向、轴向以及联合载荷分布的球轴承，文献[9]提出了一种分析其球与滚道的接触热阻的方法。文献[3]分析了不同载荷对球轴承内部接触热阻的影响。由于轴承工作过程中，有着复杂的热结构耦合关系，因此以赫兹接触理论为基础，提出了计算不同温升下球轴承内部接触热阻的计算方法。

2 角接触球轴承几何参数

2.1 轴承的结构

图1 角接触球轴承结构简图Fig.1 Structure of Angular Contact Ball Bearings

图中：Oi、Oe—内、外圈滚道沟曲率中心；di—内圈外径；de—外圈内径；dm—节圆直径，dm=（di+de）/2；rb—滚动体半径，D—滚动体直径，D=2rb。

在滚动轴承的轴向平面内，通常用密合度（Φ）来表示滚动体与滚道之间的密接程度，Φ=D/2r。滚动轴承的承载能力在很大程度上是取决于密合度的，滚动体与滚道的密合度越大，在同样负荷下的接触面积越大，应力越小，承载能力也就越高，但同时摩擦力也越大。对于各种球轴承，也经常使用滚道沟曲率半径系数f来表示滚动体与滚道的密接程度，f=r/D。在球轴承的设计中，滚道沟曲率半径系数f 是一个十分重要的参数，f 和Φ 之间满足Φ=1/2f。在没有任何外部载荷的情况下，内外滚道曲率中心之间的距离可由下式确定[10]：

2.2 轴承的温差膨胀

通常情况下，轴承在室温下安装，但它们在工作过程中由于摩擦力矩作用会产生温升，轴承在比室温高ΔT 的温度下运转[10]。由于温度的增加，材料将产生如下的线膨胀：

式中：Γ—线性膨胀系数；L—特征长度；ΔT—温度增加量。

温升导致的材料线膨胀将会使滚动轴承的几何参数发生变化。特别是滚动体直径和内、外滚道沟半径的变化，将使密合度发生变化，这将对轴承的工作特性产生明显的影响。当滚动体温度增加ΔTb时，滚动体的直径为：

式中：re0—室温时外滚道沟半径；de0—室温时的外圈内径；De—公称外径。

3 载荷分布及接触区域

3.1 负荷与变形

由赫兹接触理论，接触负荷与弹性变形之间的关系为[5]：

Q=Knδn（11）式中：Q—滚动体与内圈或外圈之间的接触负荷；Kn—滚动体与内圈或外圈之间的负荷-变形常数，与材料和几何特征有关；δ—滚动体与内圈或外圈的接触弹性变形量；n—指数，对于点接触：n=3/2，对于线接触n=10/9。对于球轴承钢球与套圈之间为点接触，钢球与某一套圈之间的载荷-变形系数Kj（j=i，e）为：

设识别框架U的n个证据为(P1,P2,…,Pn)，则证据对应的基本信任分配函数为mi(i=1,2,…,n)，其可表示为

3.2 轴向载荷下的载荷分布

角接触球轴承在轴向力Fa的作用下，所有滚动体都将产生相同的变形并承受相同的载荷。图中：Oi和Oe—初始状态下内、外圈的滚道沟曲率中心；α0—轴承的初始接触角；α—受载后的接触角，如图2 所示。

图2 轴向变形Fig.2 Deformation of Ball Bearing Subjected to Axial Load

式中：z—滚动体个数。方程是以δa为未知变量的非线性方程，可用牛顿迭代法进行求解。求解出未知量后，可带入式中求出接触区域受载情况。

3.3 接触区域

在对相互挤压的两个弹性固体的接触面形状大小、表面压力的分布以及两物体弹性趋近量进行求解时，赫兹做了一些假设。由于滚动轴承的接触情况与赫兹假设基本相符，所以赫兹理论被成功应用到滚动轴承工程学中。由赫兹接触理论，球轴承滚动体与滚道接触为点接触，接触面为椭圆，表面压力成半椭球分布，接触区域的长半轴a 和短半轴b 计算公式如下：

式中：na、nb—与接触点主曲率差F（ρ）有关的系数，求法与nδ相同。

4 球轴承内部接触热阻

所讨论的接触热阻是基于赫兹理论所确定的宏观接触区域，忽略粗糙度和波纹度的影响。轴承摩擦所产生的热量将仅仅通过轴承内部的接触区域进行传导，轴承滚动球体和内、外滚道之间的接触热阻问题可以等同于一个孤立、等温区域相对于绝缘半空间的散热和受热问题[4]。结合第一类完全椭圆积分，单个滚动球体和滚道或外滚道之间的接触热阻为[9]：

此外，把单个滚动体与内、外圈之间的热阻并联可求得滚动体与内、外圈之间总的接触热阻。对于轴承内部总的接触热阻，可由滚动球体与内、外圈之间总的接触热阻串联求得。

5 试验验证

以数控机床HTC2050i 进给驱动系统中支撑轴承型号25TAC62B（NSK）角接触球轴承为例，在室温23.0℃下，进给驱动系统预拉伸载荷500N，进给速度15m/min 进行测试，测试装置由数控机床进给驱动系统和FLUKE 热成像仪组成，测点分布及现场测试，如图3 所示。测点1 位于轴承座外表面宽度中点，测点2 位于轴伸端的端面中点，球轴承的结构参数，如表1 所示。轴承为钢制轴承，轴承材料的物理参数，如表2 所示。

图3 热成像图及测点分布Fig.3 Heat Image and Testing Points Distribution

表1 25TAC62B 的结构参数Tab.1 Structure Parameters of Ball Bearing

表2 轴承材料的物理性质参数Tab.2 Physical Properties of Bearing Materials

本试验测试机床进给速度15m/min 空载热机，每隔10 分钟采集测点温度，共计采集到60 分钟的数据。基于ANSYS 建立有限元模型辨识温度场和热阻。

轴承生成的摩擦热是一个主要的摩擦源，支撑轴承的摩擦可使用经验公式计算如下[10]：

式中：f0—与轴承类型和润滑类型相关的因子；v0—润滑油的运动粘度。

润滑油的运动粘度是温升的函数。假设内外圈滚道的发热率各占50%。并作为边界条件赋值给有限元模型，反复迭代设置滚动体与内外圈滚道的接触单元属性接触热导率系数值，直到有限元计算测点与实验测试点的温度一致，经过有限元辨识计算，获得各元件的温度分布，如图4 所示。

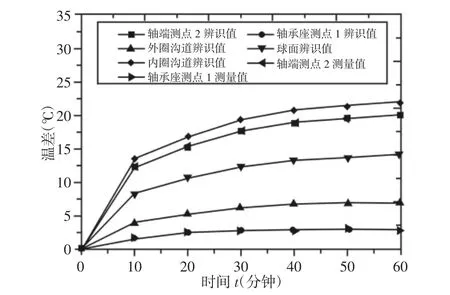
图4 主要元件温升辨识值与测量值Fig.4 Temperature Rise of Main Elements

根据实验辨识结果，由式（1）～式（2）和（5）～式（12），得出轴承接触角与温升的关系，如图5 所示。图中可见轴承接触角随温升增大而下降。

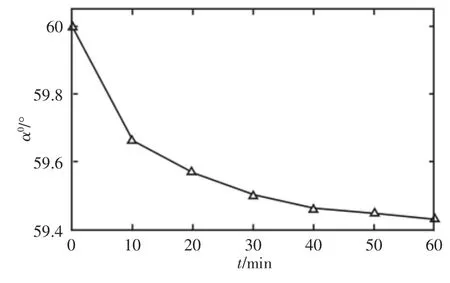
图5 温升对接触角的影响Fig.5 Effect of Temperature Rise on Contact Angle

当轴承受500N 的轴向载荷，由式（3）～式（4）和式（11）～式（22），不同温升条件下的单个滚动体所受法向载荷，如图6 所示。数据表明不同温升条件下的单个滚动体所受法向载荷，随温升增大而增大，并且解析解与辨识解吻合。

图6 温升对单个滚动体所受法向载荷的影响Fig.6 Effect of Temperature Rise on Normal Load of a Single Rolling Body

图7 温升对接触椭圆面积的影响Fig.7 Effect of Temperature Rise on the Area of Contact Ellipse

图8 温升对接触热阻的影响Fig.8 Effect of Temperature Rise on Contactthermal Resistance

在不同温升条件下，由式（23）～式（24），内、外圈接触区域的长、短半轴均变大。单个滚动体与内圈或外圈的接触椭圆面积，如图7 所示。滚动体与内圈或外圈的接触椭圆面积均随温升提高而增大，并且解析解与辨识解相近。

基于仿真数据，热阻计算公式为：

式中：ΔTs—滚动体与接触表面的温差；q—接触表面的热流率（热源功率）。

随着工作温度的升高，由式（32），轴承滚动体与内圈和外圈的接触热阻，如图8 所示。轴承滚动体与内圈和外圈的接触热阻，均随温升提高而下降，并且解析解与辨识解变化基本一致。轴承内部总接触热阻，也随温升提高而下降，如图9 所示。

图9 温升对接触总热阻的影响Fig.9 Effect of Temperature Rise on Total Thermal Resistance of Contact

6 结论

针对承受轴向力球轴承提出了轴承内部接触热阻随温升变化模型。在同一轴向载荷作用下的角接触球轴承，随着工作温度的升高，接触角减小，滚动体所受法向载荷增加，接触区域的长半轴和短半轴均变大，接触面积增大。进而导致随着工作温度的升高，轴承滚动体与内圈和外圈的接触热阻均变小，轴承内部总接触热阻也变小。