微动磨损工况下二维柱面对平面磨损形貌的数值计算与分析

唐正强，张慧杰，李 俨，张太华

（1.贵州大学机械工程学院，贵州 贵阳 550025；2.贵州大学现代制造技术教育部重点实验室，贵州 贵阳 550025；3.贵州师范大学机械与电气工程学院，贵州 贵阳 550001）

1 引言

微动是发生在两接触表面之间微、纳米量级的运动[1]。这种微小幅度的振动容易被人们忽视，却是机械零构件失效的主要原因[2]。因此，微动被认为是现代工业机械部件的癌症[3]。

众多学者对微动磨损做了大量的实验研究，研究微动工况、材料属性等因素对磨损的影响[4-8]。文献[4]研究了304 不锈钢在不同位移振幅下的微动磨损行为，结果表明304 不锈钢的磨损系数和微动损伤均随微动幅值的增大而增大。文献[5]在锆合金包壳的微动疲劳试验中研究了滑移状态下的磨损形貌、磨损体积和磨损深度等特性。文献[6]研究了热处理对316L 不锈钢表面TiO2涂层磨损的影响，结果表明热处理增强了涂层的抗磨损能力。文献[7]通过扫面电镜观察了不同接触载荷下钢丝的磨损形貌，结果表明随着接触载荷的增加，钢丝的稳定摩擦系数呈现降低趋势。文献[8]研究了偏心载荷作用下螺栓连接的松动行为，发现螺纹接触表面的微动磨损将会导致螺栓受到的轴向力下降。微动磨损对构件的影响往往在高周循环载荷之后才能体现出来，有的构件甚至要在微动工况下服役几年的时间。因此，微动磨损实验无论是从时间还是经济上都是很大的浪费，数值模拟则弥补了实验的这些缺点。

近年来，基于Archard 磨损方程的微动磨损数值模拟研究受到众多学者的关注[9-14]。文献[9]是较早应用Archard 磨损方程来模拟二维柱面与平面磨损的学者，通过对比试验研究验证了其数值模拟的可靠性。文献[10]推导了基于Archard 方程的局部磨损方程，并结合有限元法预测了材料表面磨损形貌。文献[11]利用数值模拟方法对考虑累积塑性变形的平面-平面接触问题进行了模拟研究，结果表明塑性变形量变大，最大接触应力变小。文献[12]建立了基于有限元法的二维平面-柱面微动磨损模型，并通过多层节点更新方法解决了磨损深度大于有限单元边长的问题。文献[13]基于二维柱面-平面研究了整体滑移与部分滑移对锆合金磨损速率的影响，发现磨损速率随应变载荷振幅增加而增加，磨损率在不同接触状态随法向力变化的规律不同。文献[14]利用有限元法研究了髋关节假体头颈锥度连接处的微动磨损，发现锥角的类型和大小对材料损有很大影响。

从上述研究中可知，在微动磨损实验研究进展的同时，越来越多的学者采用数值模拟的方法研究微动磨损。一方面可以节约实验所需的时间和成本，另一方面可以通过接触体磨损过程中的弹塑性变形、非对称性应力应变等变化深入探索磨损机理，提出有效抑制磨损的方法。针对微动磨损工况下接触表面磨损形貌问题，基于Archard 磨损方程推导了适应于任意微动振幅的局部磨损公式，建立了二维刚性柱面与弹性平面的微动磨损模型，研究了二维柱面半径、微动载荷与柱面弹性模量对弹性平面磨损深度、磨损宽度和磨损面积的影响。

2 微动磨损模型与数值计算方法

2.1 二维柱面-平面有限元模型

为研究在接触过程中不同参数对接触副磨损轮廓的影响，根据三维圆柱与平板接触模型，如图1（a）所示。建立二维柱面与平面的有限元接触模型，如图1（b）所示。圆柱面半径为R，长度为L，平板的厚度为t。模型通过文献[15]进行网格划分，不同的区域采用了不同的网格大小。区域Ⅰ和区域Ⅳ是柱面与平面的接触区域，使用了边长为0.5mm 的单元；远离接触的区域Ⅲ和区域Ⅵ，使用了边长为2mm 的单元；区域Ⅱ与区域Ⅴ为网格的过渡区域，使用边长为1mm 的单元。为了研究刚性柱面对弹性平面的微动磨损影响，刚性柱面按照文献[16]中“理想刚体”的定义，设置二维柱面材料的弹性模量为平面材料的1000 倍。

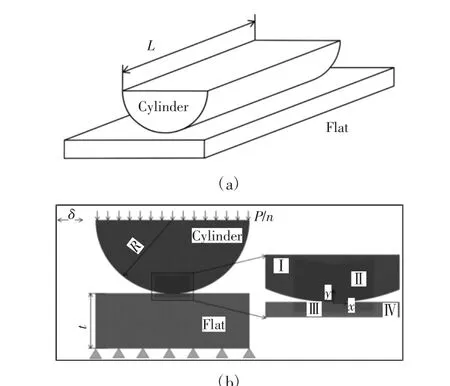
图1 微动磨损三维模型与二维有限元模型Fig.1 Three-Dimensional Model of Fretting Wear and FE Model

二维柱面与平面的接触计算采用罚函数法[17]，平面通过约束底端全部节点x 和y 方向的自由度而固定，圆柱面顶端施加载荷P/L（P 为正压力载荷，L 为圆柱的长度），同时圆柱面顶端节点上施加了平行于x 方向的往复式位移约束，如图2 所示。

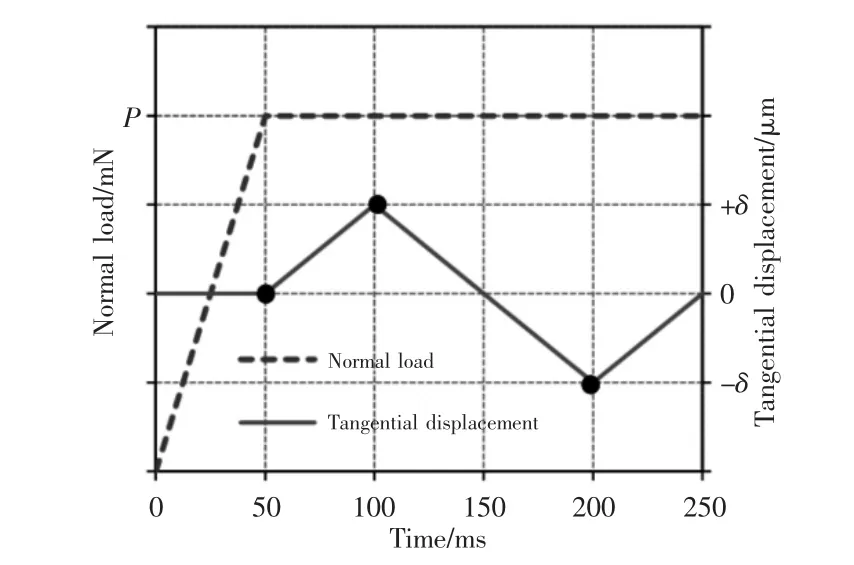
图2 正压力载荷与切向位移Fig.2 Applied Normal Load and Tangential Displacement

2.2 磨损的计算方法

为计算接触平面的磨损轮廓，基于Archard 磨损方程，文献[10]给出了式（1）来计算磨损深度：

式中：δ—设定微动振幅的幅值；n—每个微动循环子步数。微动过程中二维柱面和平面的接触示意图，如图3 所示。

图3 时间步j 到j+1 的柱面/平面的接触示意图Fig.3 Contact at the Cylinder-Flat Interface for Time Step j and j+1

每一个接触节点在不同的时间步，其接触压强不同。从图中可以看出，当时间步从j 增加到j+1 时，节点i 的接触压强从Pi，j变到Pi，j+1（其中i 为节点号，j 为时间步），则根据式（1），可得到节点i 从时间步j 到时间步j+1 的磨损深度为：

微动磨损数值模拟的具体计算流程，如图4 所示。（1）在LSDyna 有限元软件中建立二维柱面与平面的接触模型；（2）将有限元模型保存为LS-Dyna 求解器可识别的K 文件，便于后续模型的更改；（3）调用LS-Dyna 的求解器求解K 文件，计算接触压强；（4）通过MATLAB 读取结果文件，获得接触表面节点的坐标、接触压强等信息；（5）通过磨损深度计算式（6），计算在特定循环增量步内接触节点的磨损深度，获得磨损轮廓；（6）判断微动循环次数是否达到总的循环次数，若未达到，则更新二维柱面与平面的几何模型，获得更新后的K 文件，若达到预设的循环次数，则输出结果，计算结束。

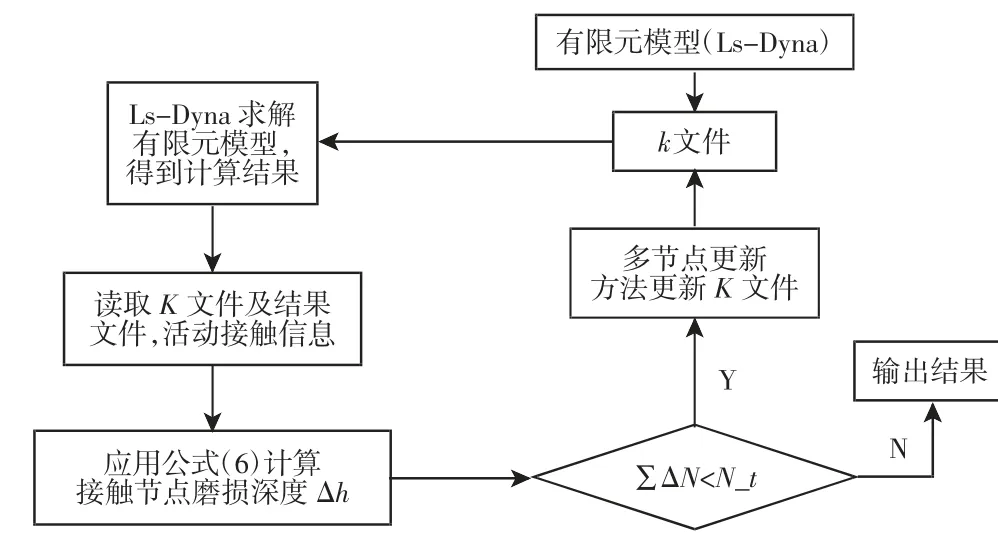
图4 微动磨损模拟流程图Fig.4 Flowchart of the Fretting Wear Procedure

3 结果讨论与分析

3.1 接触压强

为了验证这里有限元模型的正确性，比较了Hertz 接触理论与有限元模拟结果。Hertz 接触对于二维的柱面-平面的接触问题给出了接触面正压力分布的解析表达式[18]：

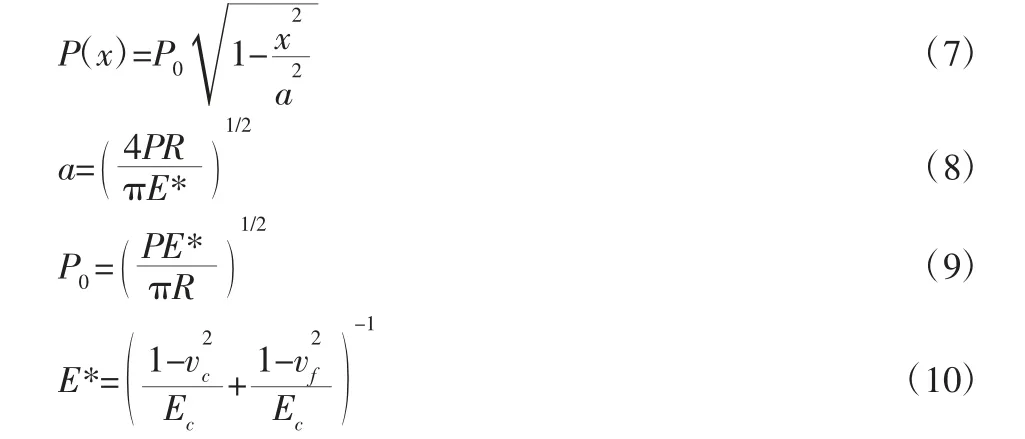
式中：p0—接触区域的最大压强；a—接触区域长度；E*—接触副材料的等效弹性模量；R—等效接触体半径；Ec、Ef—接触副材料的弹性模量；vc、vf—接触副材料的泊松比；Rc、Rf—接触副的曲率半径；“c”、“f”—柱面和平面。本模型中压力载荷设为20MPa；Ec设置为200000GPa、Ef设置为200GPa；vc、vf均为0.3。将有限元计算得到的压强与Hertz 接触理论计算得到的结果进行对比，结果如图5 所示。

图5 接触压强分布的有限元结果与Hertz 理论比较Fig.5 Comparison between Contact Pressure from FEM Analysis and Analytical Solution of Hertz

从图5 中可以看出，有限元结果和Hertz 接触理论计算结果趋于一致，但有限元结果的接触宽度值略大于Hertz 接触理论，这是由两接触面接触区域的网格单元大小引起的误差。综合考虑计算精度和磨损模型的计算时间，采取了该网格尺寸。

在不同工况下平面的压强分布，如图6 所示。从图6（a）中可以看出，随着柱面半径的增大，最大接触压强降低，接触长度增加；这是因为随着柱面半径的增大，圆柱面和平面的等效接触半径增大，导致最大接触压强降低；从图6（b）中看出接触压强也随着载荷的增大而增大；图6（c）显示了不同弹性模量下平面的接触压强变化，随着平面弹性模量的增加，由式（10）可知等效弹性模量增大，再由式（9）可知接触区域的最大压强增大。

图6 不同工况下平面的接触压强Fig.6 Effect of the Fretting Wear Conditions on Contact Pressure of the Flat

3.2 圆柱半径对磨损的影响

磨损发生在接触体表面，多数学者研究了接触副中被动磨损件结构参数对磨损轮廓的影响，而主动磨损件结构参数对磨损轮廓的研究鲜有报道。通过改变二维柱面半径研究二维柱面几何尺寸对平面磨损轮廓的影响。微动工况下（压力为20MPa，微动振幅为4μm，微动循环次数为1000 次）圆柱半径对平面磨损形貌的影响，从图中可发现，随着圆柱半径的增加，平面的磨损形貌呈现出变宽变浅的趋势，如图7（a）所示。

图7 描述了不同柱面半径下平面的磨损深度（图7（b））、磨损宽度（图7（c））以及磨损面积（图7（d））随微动循环次数的变化规律。磨损面积是指平面的磨损轮廓与原始轮廓围成的面积。从图中可以看出平面的磨损深度、磨损宽度和磨损面积随着微动循环次数的增加而增加。其次，我们发现平面磨损深度随着圆柱半径的增大而减小，磨损宽度随着圆柱半径的增大而增大。由式（11）可知，假设平面的半径Rf趋于无穷大，随着圆柱半径Rc的增大，等效接触半径R 增大，导致磨损区域接触长度a 增大。同时，在载荷不变的情况下导致接触压强减小，因此，平面的磨损深度随着Rc的增大而减小。其次，我们发现平面的磨损面积随着微动循环次数的增加而呈线性增加，另外，圆柱半径对平面的磨损面积没有影响。这是因为随着圆柱半径的增加，平面磨损深度减小而磨损宽度增加共同作用的结果。

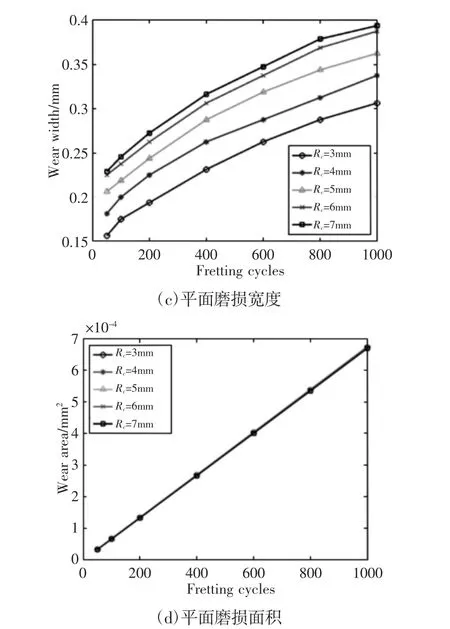
图7 柱面半径大小对平面磨损的影响Fig.7 Effect of the Cylindricalsurface Radius on Wear Performance of the Flat

3.3 载荷对磨损的影响

在1000 次微动循环次数下平面的磨损形貌，我们可以看出随着载荷的增加，平面的磨损轮廓有显著的区别，表明载荷对磨损形貌的变化有着显著影响，如图8（a）所示。

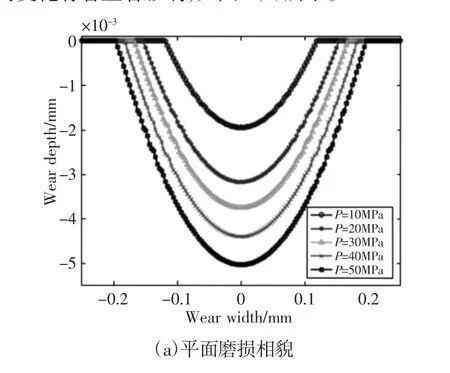
图8（b）～图8（d）描述了不同载荷作用下平面的磨损深度（图8（b））、磨损宽度（图8（c））和磨损面积（图8（d））随微动循环次数的变化规律。从图中可以看出，随着微动循环次数的增加，平面的磨损深度、磨损宽度和磨损面积均逐渐增加；同时随着载荷的增加，平面的磨损深度、磨损宽度和磨损面积也大幅增加。

图8 载荷对平面磨损的影响Fig.8 Effect of the Normal Load on Wear Performance of the Flat

3.4 弹性模量对磨损的影响

1000 次微动循环后的平面磨损轮廓，发现在不同的弹性模量下，平面的磨损轮廓改变较大，如图9（a）所示。随着弹性模量的增加，平面磨损轮廓从宽而浅变化到深而窄。

图9（b）～图9（d）显示了不同弹性模量下平面的磨损深度（图9（b））、磨损宽度（图9（c））和磨损面积（图9（d））随着微动循环次数的变化规律。随着微动循环次数的增加，平面的磨损深度、磨损宽度和磨损面积均逐渐增加；随着弹性模量的增加，平面的磨损深度增加但磨损宽度减小。从图9（d）中看出，虽然弹性模量对平面的磨损深度和磨损宽度呈现出相反的影响效果，但是随弹性模量的增加平面的磨损面积增大。此外，我们发现不同弹性模量下磨损面积与微动循环次数均呈现出线性关系。

图9 弹性模量对平面磨损的影响Fig.9 Effect of the Elastic Modulus on Wear Performance of the Flat

这里的模型基于有限元接触压强的计算和Archard 磨损公式的推导，通过迭代更新的方法计算磨损形貌。在初始接触阶段，有限元的接触压强计算结果应与Hertz 接触理论保持一致。因此，我们试想直接通过Hertz 接触理论和Archard 磨损方程来预测平面磨损面积随着微动循环次数的变化规律，与模型计算结果进行对比，如图10 所示。选取了圆柱半径Rc=5mm，载荷为20MPa，微动振幅为4μm 的工况采用两种计算方法进行磨损面积预测。从图中可以看出，在微动循环次数较低时，根据Hertz 接触理论和Archard 磨损方程预测的平面磨损面积与本论文中模型计算的结果差别不大，但随着微动循环次数的增加，Hertz 理论预测结果小于这里模型计算的结果。这是因为在模型计算过程中，随着微动循环次数的增加，弹性平面的磨损形貌实时更新，二维柱面与磨损平面的接触不再符合经典的Hertz 接触理论，加上微动振幅的作用，使得这里模型的接触半径大于Hertz 理论的接触半径，因而在磨损面积计算时这里模型计算的磨损面积值略大于Hertz 理论预测值。

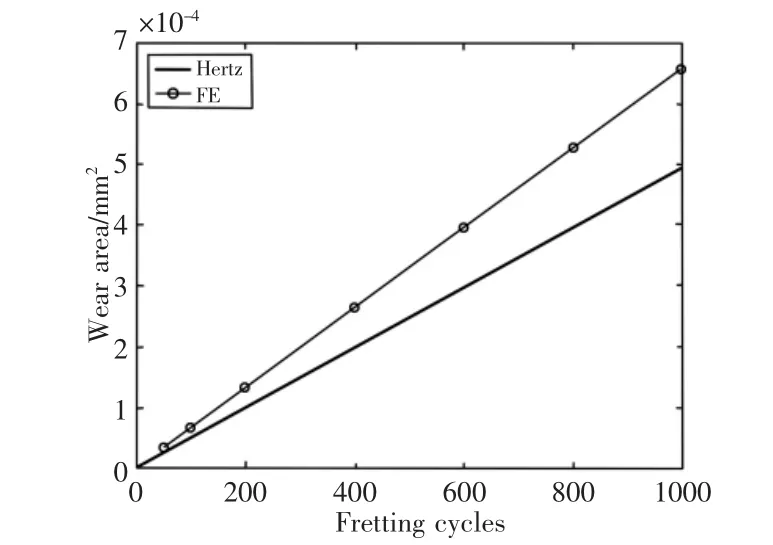
图10 磨损面积预测结果对比Fig.10 Wear Area Comparison between Hertz Theory and the Present Result

这里的模型忽略了材料的界面环境和磨粒（第三体）的参与，因此，随着微动循环次数的增加，磨损面积呈线性增加。虽然该模型的假设与真实环境中的磨损现象有差别，但能通过模型快速预测材料表面的磨损趋势，合理的选择材料参数，设计较合理的微动工况，抑制或者减缓材料的磨损，增加零部件的使用寿命。

4 结论

基于改进的Archard 磨损方程，推导了适应于不同微动振幅下的局部磨损方程，建立了二维刚性柱面-平面的数值模型。分别从平面的磨损深度、磨损宽度和磨损面积三个特征量研究了二维柱面对平面磨损形貌的影响。研究结果表明随着柱面半径的增大，平面的磨损深度降低、磨损宽度增大、磨损面积保持不变；随着载荷的增大，磨损深度、磨损宽度、磨损面积均呈现增大趋势；而随着平面弹性模量的增大，平面的磨损深度增大、磨损宽度降低，但磨损面积增大。该模型能快速预测材料表面的磨损趋势，有助于设计较合理的微动工况，抑制或者减缓材料的磨损。