基于VAR 模型的交通安全与经济损失关系研究
黄 宇,薛 锋,2
(1. 西南交通大学,交通运输与物流学院,成都 611756;2. 综合交通运输智能化国家地方联合工程实验室,成都 611756)
0 引 言
随着国家经济的快速发展,全国各地区机动车的数量也在快速增长,人们交通出行越来越便利的同时,交通事故正严重地威胁着人们的人身安全。交通事故不仅造成人的身体、心理伤害,还造成物的破坏、经济的损失,更成为危害人类生命的主要原因之一。
国内学者对于交通安全的研究多侧重于风险评估方面,如黄文成等[1]建立了一个新的道路危险品运输系统风险评价方法;李强等[2]提出了基于质量功能配置法的危险品运输风险影响因素的重要度分析方法;陈跃等[3]对前人所做的风险分级指数模型进行了改进,构建了新的危险货物道路运输风险评价指数模型;陶健[4]以陕西某危险货物运输企业和具体运输路线为研究对象,运用所建模型计算特定运输任务的事故风险,并对计算结果进行客观评价。国外学者Ntzeremes等[5]将风险评估引入公路隧道消防安全,提出了一种基于风险降低和社会经济因素的安全措施最优选择的综合框架,并讨论了其在公路隧道风险分析中的适用性;Jurewicz 等[6]应用碰撞预测风险评估模型评估道路网络未来发生严重车祸的风险,以减少严重的道路崩溃风险发生的概率。以上研究均从交通事故成因角度进行分析,以引起交通运输从业人员的警觉,极少数学者[7-8]从交通事故所造成严重经济损失的角度来分析交通安全的必要性。
鉴于此,笔者从交通安全经济效应的视角,将经济元素引入交通安全进行研究,运用向量自回归(Vectir Autoregression,VAR)模型和Granger因果关系检验等方法,定量分析交通事故发生数、伤亡人数、直接财产损失三者之间的动态关系,变量之间的格兰杰因果关系以及脉冲响应关系,以期从交通安全经济效应方面为交通管理部门建设更加安全的交通环境提供参考。
1 数值模型计算方法
向量自回归(VAR)模型作为一种非结构化的多方程模型,模型把每一个内生变量视为构建模型中的所有内生变量的滞后值函数来建构模型。将单变量自回归模型扩展为具有时间序列性质的多变量自回归模型,主要用来拟合各个变量之间的关系,模型初期用于测量股票交易的风险[9],常应用于计量经济学领域,随着模型的不断推广,可以运用在众多的领域。基于本文主要研究的是交通事故发生数(Y)与伤亡人数(X1)、直接财产损失(X2)的动态关系,因此本文利用向量自回归模型来对这三个变量之间的动态关系加以解释,VAR 模型矩阵表达式如下:
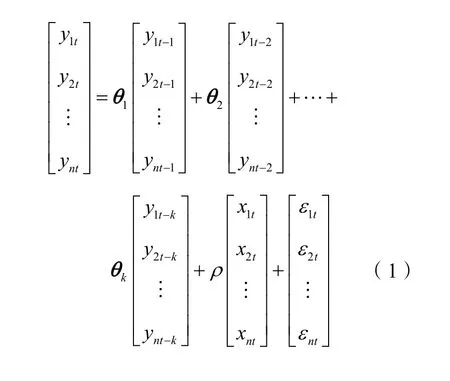
式中:θ 表示系数矩阵; yt表示内生变量向量;k 表示滞后阶数; xt表示外生变量向量;tε 表示随机干扰项。基于上述VAR 模型,将所选取交通事故发生数、伤亡人数、直接财产损失,做对数运算以消除异方差[10],再将三个内生变量带入VAR 矩阵模型可生成具体模型:


格兰杰因果关系(Granger Causality)常用于检验两个变量间的相互作用关系,是一种动态关系的检验。如果影响显著,说明该变量对另外一个变量或几个变量存在格兰杰因果关系;如果影响不显著,说明该变量对另外一个变量或几个变量不存在格兰杰因果关系检验。格兰杰因果关系检验的原假设是被检验变量不是因变量的因果关系,如果检验的概率P 值小于设定的置信水平(通常为5%),则认为被检验变量构成因变量的因果关系;反之,认为被检验变量不是因变量的因果关系[11]。在进行格兰杰因果关系检验之前,会对整理的具有时间序列性的数据进行平稳性检验,诊断其是否存在单位根。如果检验结果存在单位根,表明时间序列数据不平稳,则需要对其进行协整检验,确定其是否存在长期均衡关系。如果时间序列数据存在长期均衡状态,则可进行格兰杰因果关系检验。
2 交通事故发生数与伤亡人数、直接财产损失的关系分析
2.1 平稳性检验
在建立向量自回归(VAR)模型之前,首先要对所选取变量进行平稳性检验,这样可避免因原始时间序列数据的不稳定而造成的错误回归模型[12]。大多数学者采用 ADF(Augmented Dickey-Fuller)单位根检验方法来检验数据序列的平稳性,进而对选取的变量进行协整性检验。本文从ESP(Exome Sequencing Project)数据平台收集整理得到1990—2016 年三个变量的时间序列数据,为使检验结果更加准确,先使用ADF 单位根检验方法检验数据的平稳性,结果如表1 所示。

表1 ADF 单位根检验结果
表1 检验结果显示,交通事故发生数、伤亡人数、直接财产损失原序列数据均存在单位根,这说明数据时间序列不平稳。直接财产损失在经过一阶差分后,其ADF 值在5%水平下显著,说明数据达到平稳。交通事故发生数和伤亡人数在经过二阶差分后,两者的ADF 值也在5%水平下显著,说明数据到达平稳。现在继续进行p-p 检验,结果如表2 所示。
表2 中p-p 检验结果显示这三个变量也都在5%的显著水平下拒绝有单位根的原假设,这说明这三个时间序列数据都是平稳的,与ADF 单位根检验结果一致。
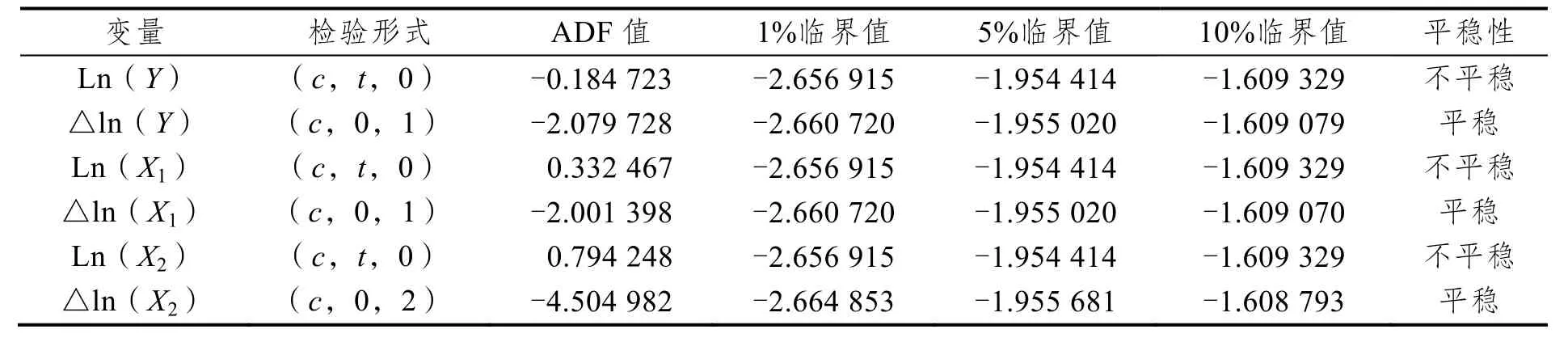
表2 数据的p-p 检验结果
2.2 VAR 模型的估计
(1)Johansen 协整检验
VAR 模型是依据数据的统计性质建立的,在建立模型之前,需要通过协整检验判断变量关系是否平稳,通过 AIC(Akaike Information Criterion)准则和SC(Schwarz Criterion)准则来确定最佳滞后阶数k,这样VAR 模型能反映出变量间相互影响的绝大部分。首先通过Johansen协整检验时间序列ln(Y)、ln(X1)、ln(X2),检验结果如表3 所示。
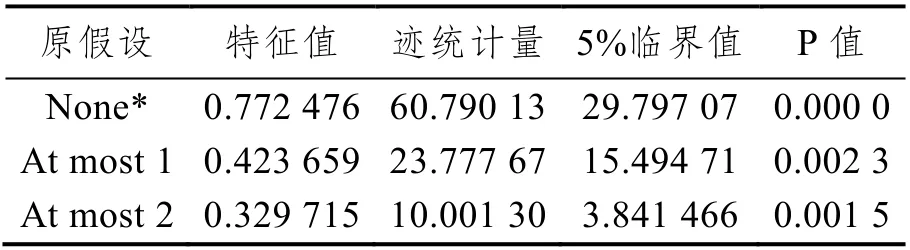
表3 变量ln(Y)、ln(X1)、ln(X2)的Johansen检验结果
由表3 检验结果可得,在5%的检验水平下,变量ln(Y)、ln(X1)、ln(X2)存在长期稳定的协整关系,也就是说交通事故发生数、伤亡人数、直接财产损失存在稳定的均衡关系。
(2)最佳滞后阶数的确定
根据最优滞后阶数应使AIC 和SC 同时取值最小的原则,当AIC 和SC 准则不一致时,应选择满足更多准则的滞后阶数。根据表4 结果,当滞后阶数为2 的时候,AIC 和SC 准则不一致,符合应选择满足更多准则滞后阶数的规则,故本模型最佳滞后阶数为2。
(3)VAR 模型的建立
在确定滞后阶数为2 后,为防止VAR 模型出现伪回归,保证VAR 模型的精确性和稳定性,利用AR 单位根检验来验证模型的稳定性,结果如图1 所示。所有的AR 特征根倒数的模都落在单位圆内,这说明VAR 模型是平稳的[13]。

图1 AR 特征根倒数的模的单位圆结果

表4 最佳滞后阶数选择
选取VAR 估计模型中的系数,构建模型估计方程如下:

2.3 Granger 因果关系检验
Ganger 因果关系检验能反映所检验变量之间的因果动态关系,根据检验结果中的P 值来判断一个变量对一个或多个变量的影响结果是否显著,也就是拒绝或者接受原假设[14]。从表5 可以看出,在5%的显著性水平下,ln(Y)与ln(X1)不存在格兰杰原因,这说明交通事故发生并不一定会出现人死亡,也不能排除交通事故不会造成人的伤亡,往往在出现严重交通事故的时候,会造成人受伤甚至出现死亡的可能;ln(Y)是ln(X2)的单向格兰杰原因,说明交通事故的发生导致人的直接财产损失进而给国家经济造成损失。一是交通事故发生后,交通工具出现损伤需要修复,特别是汽车等大型交通工具需要大量的材料修复;二是事故的清除需要大量的人力、物力,也会造成经济的损失;三是交通事故发生数越多,对财产的损失越严重。ln(X1)与ln(X2)互为格兰杰原因,交通事故造成的人员伤亡直接造成了财产的损失,包括医药费等,另外还间接地造成了人的误工费、时间成本损失等不可定量的财产损失。
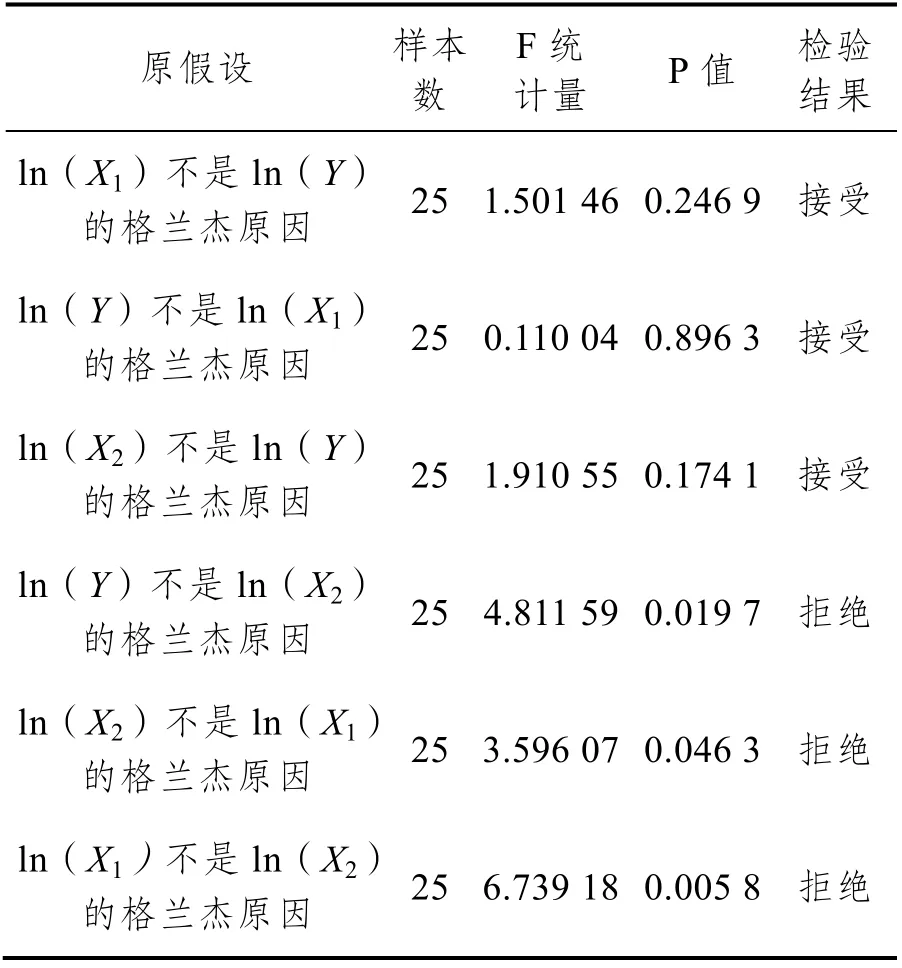
表5 格兰杰因果关系检验结果
2.4 脉冲响应分析
脉冲响应函数可用于衡量来自随机扰动项的一个标准差冲击对内生变量当前和未来取值的影响,其变动轨迹能比较直观地刻画出变量之间的动态交互作用及其效应[15]。因此,本文利用上述建立的VAR 模型,借助脉冲响应函数分析得到三个变量之间的脉冲响应图和脉冲响应值,进一步分析变量间的动态关系。对数据进行分析后,得到三个变量的脉冲响应曲线(见图2)以及脉冲响应分析结果(见表6)。
据图2 和表6 结果可以,交通事故发生数在当期对伤亡人数、直接财产损失分别为0.061 981、0.054 065,说明交通事故一发生就对伤亡人数、直接财产损失有很大的冲击;在随后的几期响应值中,数值表现为忽高忽低,但10 期总累计值为正,这说明交通事故的多次发生,会造成严重的直接财产损失和人员的伤亡。
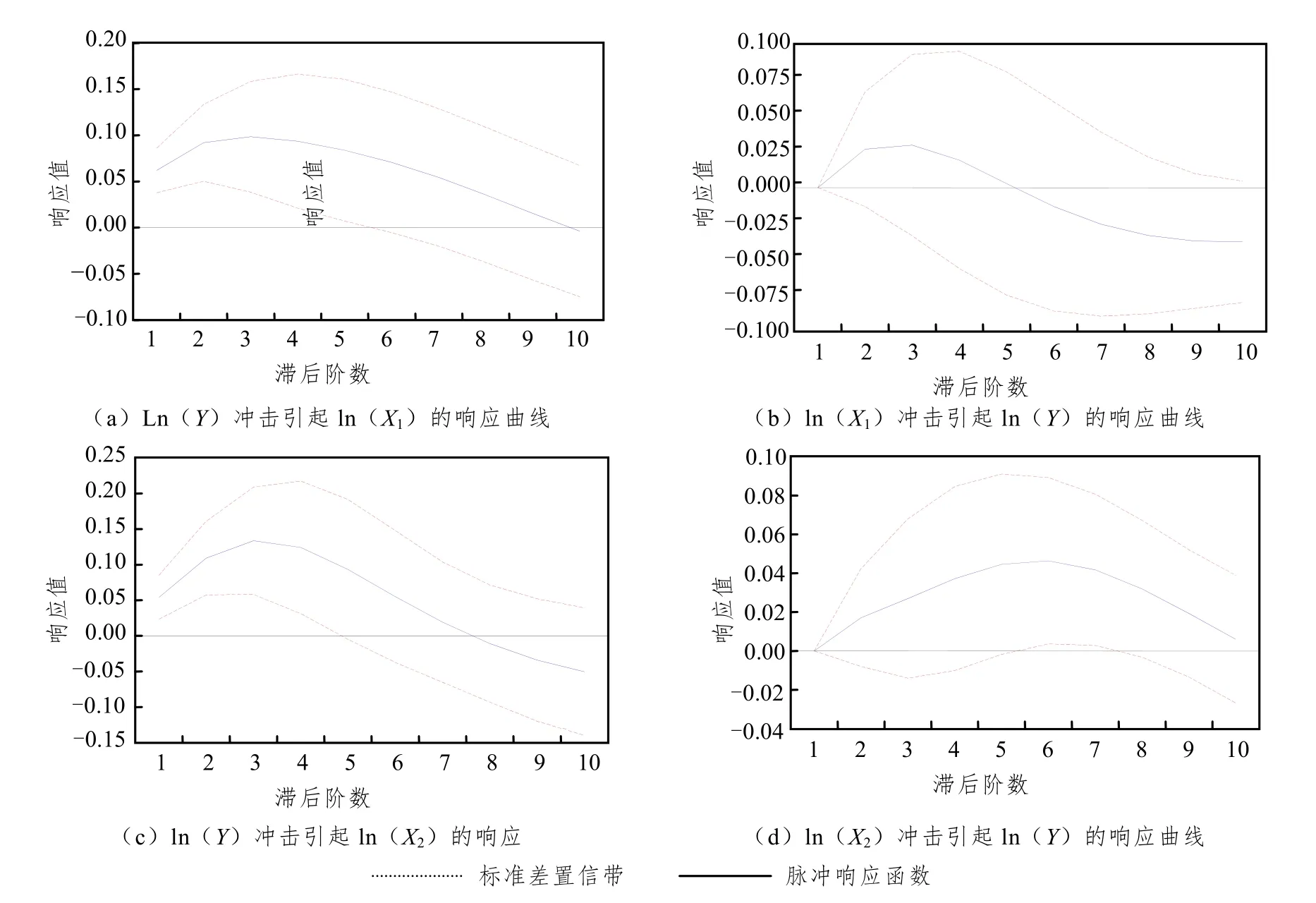
图2 脉冲响应曲线

表6 脉冲响应分析结果
3 结 论
上述定量分析结果表明,交通事故发生数对伤亡人数、直接财产损失的冲击效果正逐渐降低,这说明在现有的交通管理政策下的交通事故发生数已得到有效的控制,且交通事故发生数直接影响经济损失的严重程度。根据VAR 模型结果可得到以下3 点结论,交通管理部门可参考以下结论,从经济角度制定相应的交通管理政策:
(1)从三个变量之间的格兰杰原因分析,交通事故发生数是直接财产损失的格兰杰原因,事故伤亡人数与直接财产损失互为格兰杰原因;交通事故次数的多发在一定程度上造成人身伤害,更是造成直接财产损失的主推手。
(2)从三个变量之间的脉冲函数冲击响应分析可知,交通事故发生数对伤亡人数、直接财产损失都长期存在正向的冲击,且交通事故发生数对于直接财产损失影响更为显著,这说明交通事故是造成人员伤亡和直接财产损失的主要原因,交通事故对人及物的危害极大。
(3)从经济视角对交通安全进行分析,经济增长带动了国家机动车保有量的大幅度增加,创造一个安全的交通环境,能减少交通事故、减少人员伤亡和直接财产损失,间接促进经济的增长。
交通事故发生最为直接的影响就是造成人员伤亡和财产损失,本文基于ESP 数据平台对因交通事故发生数而造成的经济损失进行VAR 模型分析,一定程度上可以证明交通事故对经济损失的冲击力度,但未能区分不同类型的交通事故造成经济损失的大小,需进一步深化研究。
——兼论“二维码偷换案”

