解决冲突证据合成问题的改进D-S证据理论算法

宋香鹏，肖建于，吴克凤，伏明兰

(淮北师范大学 计算机科学与技术学院，安徽 淮北 235000)

证据理论由Dempster提出[1]，之后其学生Shefer在原有的基础上进一步补充扩展，并在《证据的数学理论》(A Mathematical Theory of Evidence)中将证据理论的思想推广开来，证据理论也因此被众多学者探讨研究，所以又被称为D-S证据理论[2].近些年，信息融合研究领域备受关注.是因为研究传感器信息融合可以更好地利用传感器资源，并且通过对多源信息的组合与优化，可以推导出更多的有效信息.而D-S证据理论就是在解决多源信息不确定性度量上更接近人的思维习惯，并且推理机制相对简便.被广泛应用到军事指挥[3]、信号处理[4]、状态识别[5-6]、故障诊断、采矿冶金、智能决策、情感识别等领域.

为解决冲突证据的合成问题，国内外学者提出了许多方法来解决此类问题.较早时期的Lefevre等[7]提出将全局冲突按照相应的比例重新分配的统一信度函数组合方法，但是当证据高度冲突时，风险系数无法计算.Sun等[8]提出利用平均化冲突系数对证据体的权重进行优化分配，然后根据改进的合成规则进行计算，与实际联系存在一定的不足.张欢等[9]提出结合皮尔逊相关系数来修改证据体权重和BPA中零因子的修正，但是皮尔逊相关系数在只有一个重叠项时，无法满足数学规则.其实，研究人员对改进冲突证据的组合方法大体上分为两种，一种是对原始证据源的修正，另一种是对组合规则框架修改.对原始证据源修正这种方法虽然保留了D-S证据理论的优良数学性质，但是却忽略了证据体间的相关性；对组合规则框架修改这种方法可以很好地处理证据融合，但是在实际运用中却存在着一定的局限性.

本文首先具体分析了D-S证据理论的基本性质及其无法解决的悖论问题，总结出冲突问题的产生是因为在证据合成时，无法将交集为空的焦元的信任函数处理恰当.在实际多传感系统中，考虑到各传感器得到的证据存在着相关关系.本文提出一种结合斯皮尔曼等级相关系数的证据合成方法，首先计算出证据之间的相关系数并且得到相关性矩阵，通过相关性矩阵构造修正系数来折扣基本可信度分配函数，较大程度上减少分配整体非相关证据体的权重.最后，利用改进的D-S证据理论组合规则对修正后的证据进行合成计算.

1 传统D-S证据理论及其存在的问题

1.1 D-S证据理论

识别框架：设Θ为识别框架，且识别框架Θ中各个元素互相独立，其中识别框架Θ的所有子集组成的集合称为Θ的幂集，常用2Θ表示，它的元素个数记为2|Θ|.

基本概率分布：其中基本信任分配函数m表示是从一个集合2Θ到[0,1]的映射，A表示识别框架Θ的任一子集，记作A⊆Θ，满足以下条件[10]：

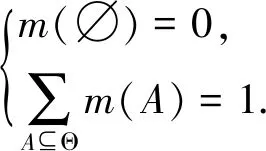
(1)

组合规则:设m1,m2,…,mn是同一个识别框架Θ下的n个基本信任分配函数，其中焦元表示为Ai(i=1,2,…,N)，则D-S的合成规则为[10]：

(2)

1.2 D-S证据理论合成规则的基本性质

在所有研究改进的D-S证据理论合成规则的前提条件下，须满足以下四个基本性质[11]：

性质1 交换律

m1⊕m2=m2⊕m1.

(3)

满足交换律的意义是当证据合成时，合成计算得到的结果并不会因为证据排列顺序变化而变化.

性质2 结合律

m1⊕m2⊕m3=(m1⊕m2)⊕m3=m1⊕(m2⊕m3).

(4)

满足结合律的意义是当多组证据合成时，可以任意组合证据的合成且每个证据的参与合成顺序不影响合成的结果.

性质3 极化性

极化性的意义是假设在m元素识别框架下n个相同证据合成后，单元素焦元总的信任分配值增加，m元素焦元的信任分配值减小，且m越大越明显.

性质4 鲁棒性

鲁棒性是指在多个证据合成时，基本信任分配函数的变化引起合成结果变化的幅度，其中这变化幅度即是鲁棒性的量化体现[12].

1.3 D-S证据理论存在的问题

因为信息具有多源和复杂的特点，所以在D-S证据理论合成时出现多种冲突证据合成的负面问题[13]，主要有分为以下四类.

1) “一票否决”问题:证据合成时，若其中某条证据与其他证据完全不一致时，则此条完全不一致的证据会完全否定合成结果，即出现一票否决的结果.

2) “证据失效”问题:即证据体在合成中不起作用.

3) “置信冲突”问题:在证据的信任函数严重矛盾时，会导致不合情理的结果出现.

4) “鲁棒性”问题:得到的合成结果会因为焦元的基本信任函数发生微小变化而产生较大的变化.

例1 完全冲突,多传感器系统收集的多个证据，得到的焦元如表1所示.

表1 完全冲突证据的BPATab.1 BPA of complete conflict evidence

完全冲突:此识别框架下，计算出冲突系数K=1,但是在D-S证据理论合成公式中分母为0，不满足数学规则，故此现象称为完全冲突，完全冲突下会造成信息的损失.

例2 0信任冲突,多传感器系统收集的多个证据，得到的焦元如表2所示.

表2 信任冲突证据的BPATab.2 BPA without trust evidence of conflict

0信任冲突:此识别框架下，计算出K=0.955，虽然m1和m3都支持A，但是m2(A)=0,完全否定了A，合成的结果为0，导致融合失败，出现一票否决的问题，传感器系统中则会因为少数传感器检测结果异常，导致整个系统无法正常运转.

例3 1信任冲突,多传感器系统收集的多个证据，得到的焦元如表3所示.

表3 1信任冲突证据的BPATab.3 BPA of absolute trust conflict evidence

1信任冲突:此识别框架下，计算出K=0.999,合成后的结果为m(B)=1，但是给出的三个证据对B的支持很小，显然违背常理，产生置信冲突问题，传感器系统中则会因为对低支持度的信息产生过多信任，导致整个传感系统准确性降低.

例4 冲突系数失效,多传感器系统收集的多个证据，得到的焦元如表4所示.

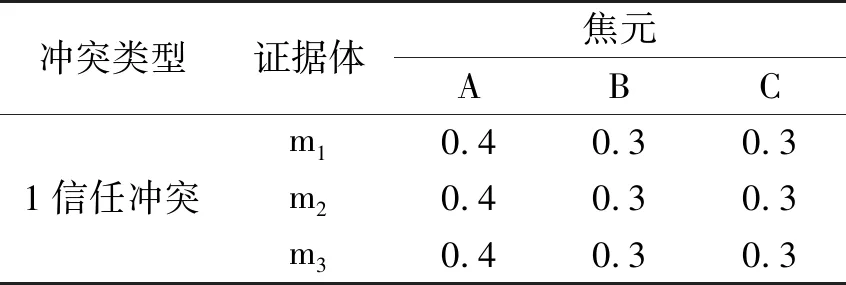
表4 冲突系数失效的BPATab.4 BPA with conflict coefficient failure

冲突系数失效:此识别框架下，计算出K=0.882，表明证据是高度冲突的，但是这是三个完全相同的证据.造成冲突系数K失效，不能很好的描述此种识别框架下的关系.

2 基于修正系数的改进算法描述

2.1 斯皮尔曼等级相关系数

斯皮尔曼等级相关系数(Spearman’s rank correlation coefficient)又称为秩相关系数，用希腊字母ρ表示.此相关系数是衡量统计变量X,Y的依赖性的非参数指标(衡量分级定序变量间的相关程度)，并且还可以通过利用单调方程来具体量化统计变量间的相关性.其中ρ的取值范围是[-1,1]，ρ的公式为：

(5)

di=xi-yi,1≤i≤n.

(6)

两个统计变量X,Y(或者是两个集合)，它们的元素个数均为n，两个统计变量取的第i个值分别用Xi、Yi表示，其中i的取值范围是1≤i≤n.对X,Y进行排序，得到两个元素排行集合x、y，其中元素xi、yi分别为Xi在X中的排行以及Yi在Y中的排行.di即为元素间的排行差.

2.2 构造修正系数方法

设m1,m2,…,mn是同一识别框架Θ下的n个基本信任分配函数，焦元分别为Ai(i=1,2,…,N).对mi按照mi(Ak)从大到小排序，其中降序序列中的每个mi(Ak)在原始序列中的位序标记为ri(Ak)；对mj按照mj(Ak)从大到小排序，其中降序序列中的每个mj(Ak)在原始序列中的位序标记为rj(Ak).若m(Ak)中有值相同的数据，则其位序值取相同数据在降序序列位序的平均值.将mi,mj看作成统计变量中的X,Y.故其秩次差为：

dk=rj(Ak)-ri(Ak).

(7)

则mi与mj的斯皮尔曼等级相关系数即为：

(8)

利用式(7)和式(8)计算出各个证据体间的斯皮尔曼等级相关性系数，然后构造证据相关性矩阵Simij，即为:

其中ρmimj为证据体mi与mj的斯皮尔曼等级相关系数(1≤i≤n,1≤j≤n).

由于斯皮尔曼等级相关系数的计算仅使用了数据的秩值，并未使用原始数据，故可将相关系数结果ρ小于等于0的赋值为0.001，以控制非正相关的证据体在识别框架中的可信度和权重占比计算，从而降低非正相关的证据体对于整体识别框架的基本概率分布的影响，同时可以克服组合规则中的置信问题.

(9)

2.3 改进冲突证据融合方法

在2.2中通过计算斯皮尔曼等级相关系数得到相关性矩阵，并且优化ρ的取值，计算得到修正系数cre.现将得到的修正系数cre对原始的基本可信度分配函数进行修正.公式如下:

mi′(Ai)=cre(mi)×mi，

(10)

mi′(Θ)=cre(mi)×mi(Θ)+(1-cre(mi)).

(11)

最后，利用D-S证据理论的组合规则进行合成，计算出融合结果.归纳总结，本文的算法步骤如下.

1)利用公式(7)和(8)计算出证据体m1,m2,…，mn间的相关系数ρmimj.

2)根据计算出的相关系数得到证据相关性矩阵：

3)将相关性矩阵中相关性值小于等于0的值赋值为0.001.

4)利用式(9)计算出归一化后的修正系数cre(mi).

5)利用式(10)和式(11)计算出修正后的基本可信分配函数mi′(Ai).

6)根据D-S证据理论合成规则计算，得到融合结果.

例5 某传感系统中的识别框架下，给出的命题P={{A},{B},{C},{D}}，相应的证据体如表5.

表5 基本算例Tab.5 Basic example

计算的详细步骤如下所示.根据式(7)和式(8)计算证据体之间的斯皮尔曼等级相关系数.首先计算m1和m2的斯皮尔曼等级相关系数如表6.

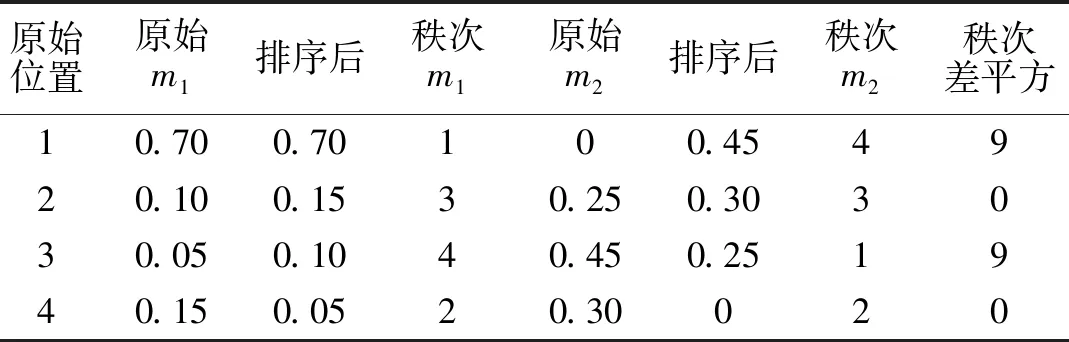
表6 证据体间的斯皮尔曼等级相关系数Tab.6 Spearman rank correlation coefficient between evidence bodies

由表6可知秩次差平方将其代入式(8)，计算出m1和m2的斯皮尔曼等级相关系数为：

依次类推，分别计算出证据体间的相关系数.得到的相关性矩阵为:

将相关性矩阵中相关性值小于等于0的值赋值为0.001,得到的新矩阵为：

计算修正向量为：

将其进行归一化处理：

由式(10)和式(11)得到修正后的基本可信度分配函数为：

P′={{A′},{B′},{C′},{D′}},

m′={0.523 0,0.188 2,0.157 1,0.131 7}.

最后利用D-S证据理论的组合规则计算出最终结果为：

P={{A},{B},{C},{D}},

m={0.971 4,0.016 9,0.007 8,0.003 9}.

3 实验分析

本章节利用传感系统中经典的算例，通过对比分析结果，表明本文提出的改进算法在解决冲突证据时符合客观实际，并且有良好的收敛性和鲁棒性.

经典算例如表7所示.不同算法对此经典算例的计算结果如表8所示.

表7 经典算例Tab.7 Classical example

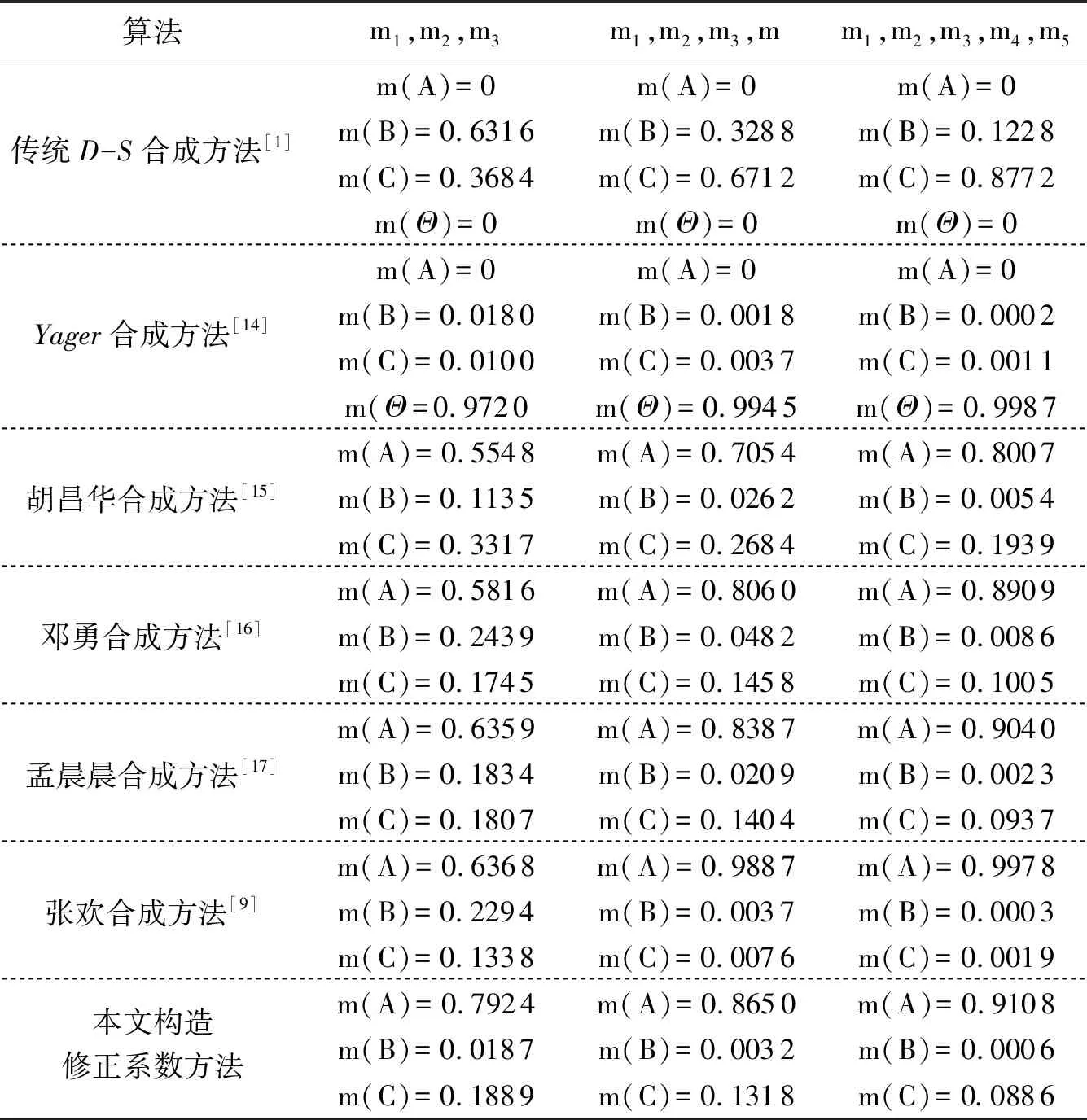
表8 不同算法对不同数量证据体的融合结果Tab.8 The fusion results of different algorithms on different numbers of evidence bodies

通过结合D-S证据理论基本性质以及实验对比分析，得到的结论如下：

传统的D-S证据理论合成方法，其缺陷就是无法合成高冲突的证据.当高冲突证据合成时，其中此条高冲突证据会完全否定合成结果，即出现“一票否决”的结果.

Yager[14]合成方法，此方法是把存在的冲突证据部分分配给识别框架全集，但是随着证据体数目增加，m(Θ)也逐渐增加，造成合成的结果不确定性增加，无法有效的辨识出目标结果.

胡昌华等[15]提出的基于修改证据的权重系数处理证据冲突，虽然收敛速度较快，但是当证据体数目逐渐增加时，该方法的目标辨识率仅达到80.07%，显然合成结果的准确性并不优良.

邓勇等[16]提出的处理冲突证据的方法，虽然结果符合常理，但是与本文算法进行比较，明显得出此方法准确性不高.

孟晨晨等[17]提出可信度和虚假度两个概念，并且引入证据间的距离公式，得到修正系数.通过折扣转换计算出合成结果，该方法能很好保护D-S证据理论优良的数学特性.但是其收敛速度并不理想，与本文提出的算法相比，本文方法的收敛性更好，收敛速度更快，并且目标辨识率提高到了91.08%，证据数目不断增加，本文的辨识率越高.

张欢等[9]提出的基于皮尔逊相关系数的改进D-S证据理论方法，在证据数目为3时，本文的目标辨识率达到了79.24%，在证据数目增加时，张欢提出的改进算法得到的效果最好，但是其忽略了皮尔逊相关系数的限制条件.皮尔逊相关系数的限制条件数据必须是连续数据，并且分布方式为高斯分布才能使用此相关系数.在例4中运用此方法是无效的，因为皮尔逊相关系数无法计算此类证据体，分母为0是其核心矛盾点.在与本文算法对比可知，本文算法适用性更广，对证据体的要求没有文献[9]中严格.

在3组对比实验中，本文提出的利用斯皮尔曼相关系数构造的修正系数算法得到m(A)的融合结果普遍高于其他学者改进的算法如图1所示；伴随着证据体数量增加，此方法表现出更高的合理命题信任度.并且在证据量较少时，本文算法有着很高的目标辨识率.

其中此实验对焦元B和C合成结果变化趋势如图2、图3所示.

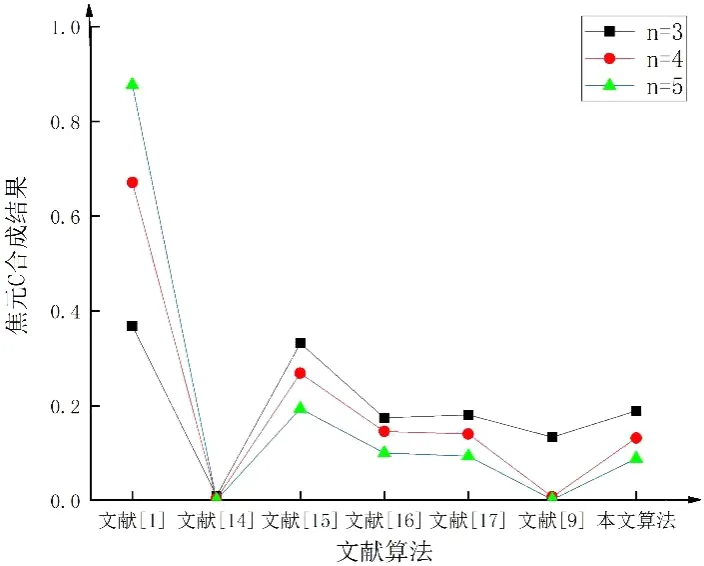
图3 不同算法对不同数量证据体下焦元C 合成结果的变化趋势Fig.3 The trend of different algorithms to the results of coke C synthesis in different numbers of evidence bodies

4 结论

本文通过利用斯皮尔曼相关系数求出证据体间的相关性矩阵，将相关性矩阵中相关性值小于等于0的值进行优化赋值，然后构造修正系数来修正证据间的冲突.最后，利用D-S证据理论组合规则对修正后的证据进行合成.通过实验对比分析，得到该算法特点如下：

引入统计学三大相关系数之一的斯皮尔曼等级相关系数来计算证据体间的相关性，有效简化了构造距离公式的过程，收敛速度更快.

通过利用相关性矩阵构造的修正系数，合理优化折扣基本可信度分配函数，同时可以克服组合规则中存在的置信问题，提高了目标辨识的准确性.

在处理高度冲突证据时，该算法在低数量的证据下，对目标辨识率很高，伴随着证据量的增加，本文算法较其他算法有一定的提高，并且在应用范围上更加广泛，能够处理不同数学分布的证据体.