微型磁纳米软体机器人的三维磁场模型及仿真

温旭琴，靳 龙，山石姣，王亚斌， 于立红，马吉明*

(1.郑州轻工业大学 计算机与通信工程学院，郑州 450002; 2.河南省民族中等专业学校 电子技术系，郑州 450008)

微型磁纳米软体机器人的尺寸足够小且表面具有疏水性和生物相容性[1]，可以无创地进入血液组织和人体器官这些特殊的密闭环境中[2]，可应用于靶向药物传输和微创手术，具有潜在的医疗应用前景[3-4].因为磁场可以穿透大多数材料并可以直接将力和力矩施加在磁性材料上，并且不会对人体组织造成损伤[5]，所以在流体环境中利用外磁场对微型机器人进行无缆驱动和控制已成为一种发展趋势[6].

Eric Diller等[7]设计了由5个独立线圈组成的一种基于黏滑运动的微型机器人驱动系统，该系统可以驱动机器人做向前的黏滑运动.另外，还有基于平面旋转磁场来驱动微型机器人运动的磁场驱动系统，Donghak Byun等[8]设计了两组方形亥姆霍兹线圈组成的磁场发生装置，Sukho Park研究小组[9]利用两组圆形亥姆霍兹线圈设计了可以生成旋转磁场的电磁驱动系统.为了使各类微型机器人能有更多自由度的运动，国内外的研究人员对磁驱动控制研究也从一维二维驱动逐渐深入到更加实用的三维磁场驱动[10].大连理工大学的李辉、张永顺[11]提出了一种由3组正交的方形亥姆霍兹线圈嵌套产生旋转磁场的磁驱动装置，该装置通过实验验证了机器人可以任意调整其姿态并且在复杂弯曲的环境内进行转弯驱动，但对于磁场方位控制的灵活性较差.

为了实现微型磁纳米软体机器人在外磁场作用下的灵活驱动控制，在运动空间产生均匀的磁场是微型磁纳米软体机器人运动控制的关键.本文通过坐标变换和磁场矢量叠加原理建立3组圆形亥姆霍兹线圈空间内产生的磁场模型，并且通过正交变换原理，以旋转磁场法向量与各轴的夹角为控制变量，推出旋转磁场的叠加公式.通过多物理场仿真软件COMSOL进行磁场模型的仿真实验，首先对由3组正交的亥姆霍兹线圈组成的外磁场驱动装置空间内磁场的均匀性进行了分析，然后对旋转磁场的方向和均匀区间范围进行了仿真研究，通过分析为驱动微型磁纳米软体机器人奠定了理论基础.

1 3组正交的亥姆霍兹线圈磁场建模

1.1 单组亥姆霍兹线圈模型

亥姆霍兹线圈是由一对彼此平行共轴圆形线圈组成的，两个线圈匝数相等，线圈内的电流大小相同，方向一致，且两线圈的间距正好等于圆形线圈的半径[12].如图1所示.

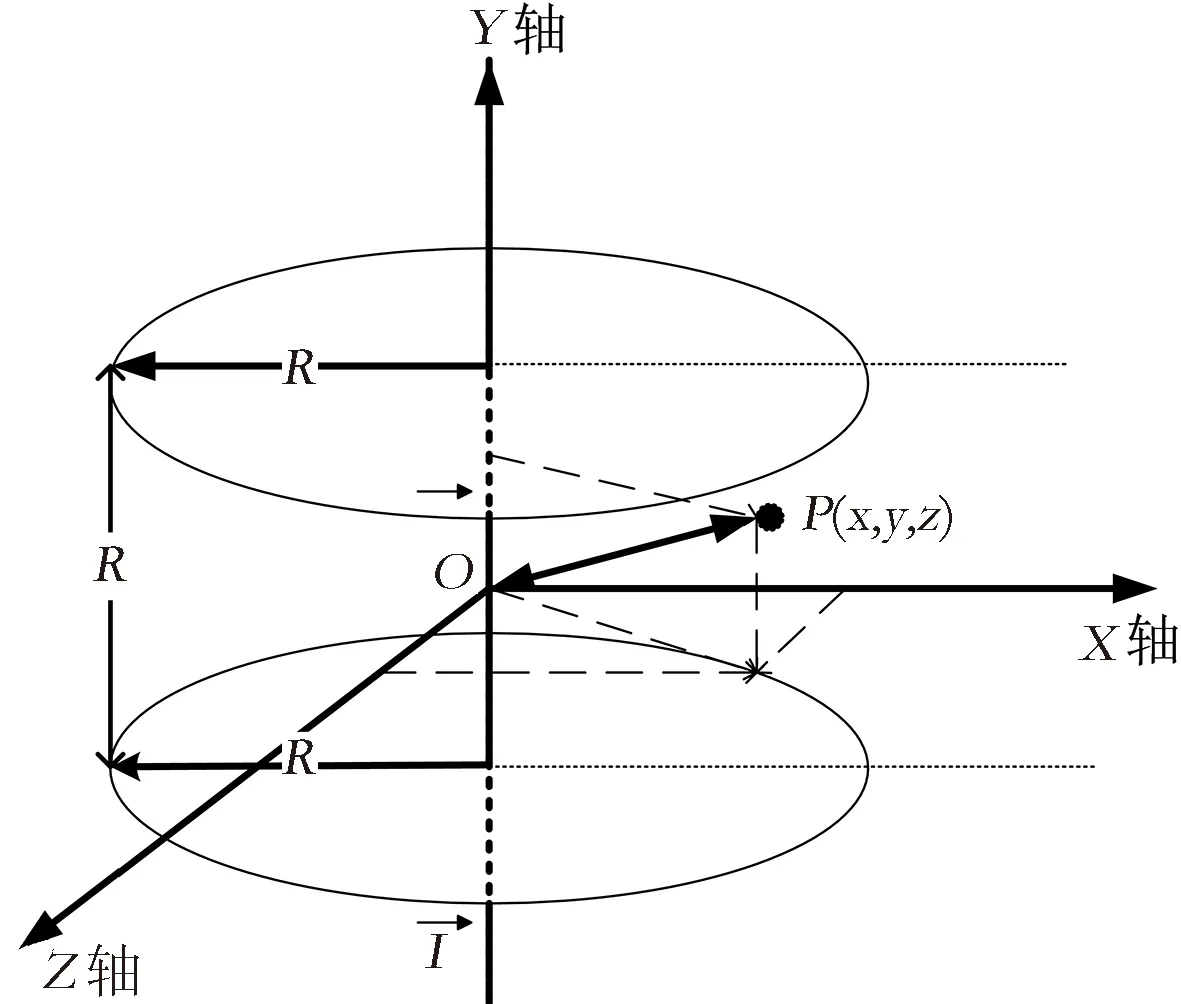
图1 y轴亥姆霍兹线圈示意图Fig.1 The forms of large-scale network survivability associations

由毕奥-萨伐尔定律[13]可知，亥姆霍兹线圈空间内的任意一点P的磁感应强度B(P)为：

(1)

其中，μ0是真空磁导率，值为4π×10-7N/A2，R为线圈半径，N为线圈匝数，I为输入线圈电流，r为点P点到中心点O处的距离，P的坐标为(x,y,z).特别地，当x=0,z=0时，r=y，代入公式(1)可以得到y轴上任一点磁感应强度表达式:

(2)

由式(2)可得，在y=0处磁感应强度最大，在y=0处对By进行泰勒展开，可以得到：

(3)

如果式(3)在y=0处的各阶倒数均为0，那么说明零点附近的磁感应强度B(y)→B(0)，可以证明在零点附近存在均匀磁场[14].因为By为偶函数，奇次项的导数为0，则对应磁感应强度的二阶导数：

(4)

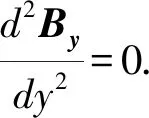
By=B0+ο(y4).

(5)

其中o(y4)代表y的4次方乃至更高幂次的小量，可以证明By在y=0的附近区域内是均匀的，可以表示为：

(6)

1.2 3组正交的亥姆霍兹线圈磁场模型

将3组亥姆霍兹线圈两两正交放置，根据磁场矢量叠加原理可以得到磁场坐标原点处的磁感应强度的矢量表达式：

(7)

磁场的模值为：

(8)

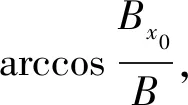
1.3 旋转磁场模型

当不同线圈组施加一定相位差的交变电流，空间磁场矢量叠加可以产生方向和大小均可调的旋转磁场，旋转磁场B(t)定义为磁场方向绕单位向量n旋转的磁场，如图2所示.旋转磁场[15]:

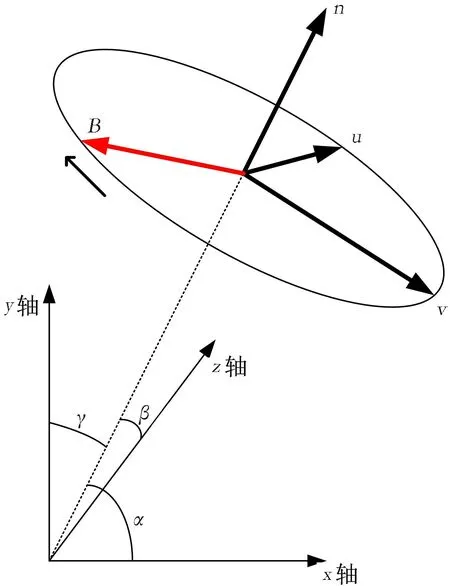
图2 旋转磁场Fig.2 Rotating magnetic field

B(t)=B[cos(2πft)u+sin(2πft)v],

(9)

u是位于旋转磁场B的平面上和向量n正交的基向量，ν表示的是旋转磁场旋转平面上垂直于n和u的基向量.本文设单位向量n的坐标为(cosα,cosβ,cosγ),其中α、β、γ分别为单位向量n与x轴、y轴、z轴的夹角.向量u和向量n正交，所以向量u的坐标可以设为(cosβ,-cosα,0).向量v和向量n、向量u两两正交，可以用向量n和向量u的外积来定义向量v，坐标为(cosαcosγ,-cosβcosγ,-cos2α-cos2β).

旋转磁场B表示为:

(10)

其中f为旋转磁场的旋转频率，t为时间，B0为圆心处旋转磁场的模.

2 3组正交的亥姆霍兹线圈磁场有限元仿真

2.1 3组正交的亥姆霍兹线圈模型的构建

采用多物理场分析软件COMSOL仿真软件对3组正交的亥姆霍兹线圈进行有限元几何模型的构建，通过求解偏微分方程组来实现对单物理场或多物理场的物理现象的仿真，COMSOL多物理场有限元仿真具有丰富的后处理交互界面，便于对仿真数据进一步分析[16].首先，新建一个三维模型，在物理场中选AC/DC中的磁场(mf)，然后添加静态研究.由公式(6)可知，当每组亥姆霍兹的线圈匝数和线圈半径的比值相等且3组线圈通入大小相等、方向相同的电流时，可以使亥姆霍兹线圈在坐标原点处产生大小相等的磁感应强度，线圈参数如表1所示.最后根据表1中理想的线圈半径和线圈匝数建立3组正交的亥姆霍兹线圈的几何模型，仿真模型如图3所示.

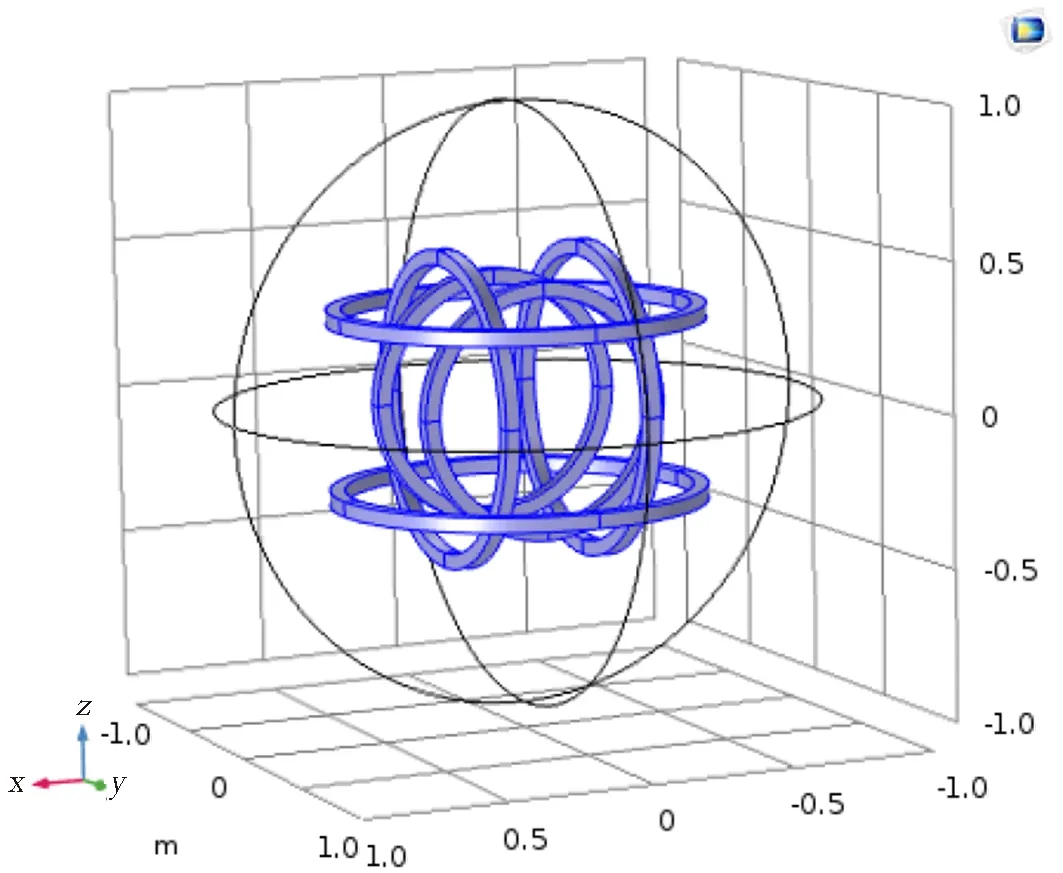
图3 3组正交的亥姆霍兹线圈仿真模型Fig.3 Three groups of orthogonal Helmholtz coil simulation models

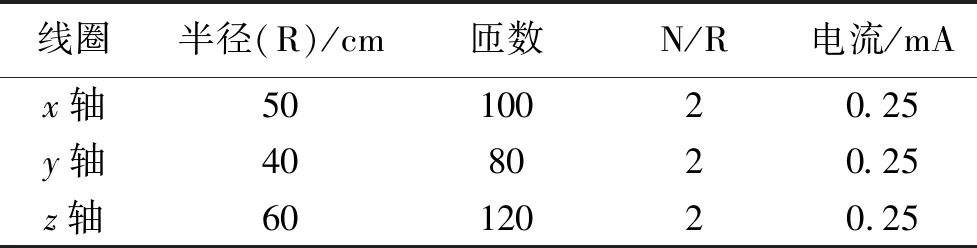
表1 3组正交的亥姆霍兹线圈参数Tab.1 Parameters of three sets of orthogonal Helmholtz coils

2.2 每组亥姆霍兹线圈磁场的均匀性分析

在模型构建完成后，分别对每组亥姆霍兹线圈磁场进行有限元仿真研究，仿真结果如图4、5、6所示.

图4代表了x轴亥姆霍兹线圈产生的磁场分布情况：(a)图是xoy平面上的磁通密度图，可以看出坐标原点处的一定区域内体箭头疏密间隔相同且方向一致；(b)图是在z轴上磁场的磁通密度模的变化情况，表明坐标原点附近的区域内磁场磁通密度模相等.上述仿真结果证明了原点附近的区域内存在均匀磁场.分别对y轴和z轴的亥姆霍兹线圈的磁场分布情况进行分析，得到了相同的结论.

(a) 0 s时的各轴相对偏差 (b) 0.25 s时的各轴相对偏差图8 0 s和0.25 s时x轴、y轴、z轴轴线上各点的磁感应强度与坐标原点处磁感应强度的相对偏差Fig.8 Relative deviation of the magnetic induction intensity of each point on X axis,Y axis and Z axis from the origin of coordinates at 0 s and 0.25 s

(a) t=0 s (b) t=0.25 s

(a) x轴亥姆霍兹线圈在x-z平面的磁通密度模 (b) x轴亥姆霍兹线圈在z轴上的磁通密度模大小变化图4 x轴亥姆霍兹线圈的磁场仿真结果分析Fig.4 Analysis of magnetic field simulation results of x-axis Helmholtz coil

(a) y轴亥姆霍兹线圈在y-z平面的磁通密度模 (b) y轴亥姆霍兹线圈在x轴上的磁通密度模大小变化图5 y轴亥姆霍兹线圈的磁场仿真结果分析Fig.5 Analysis of magnetic field simulation results of y-axis Helmholtz coil

(a) z轴亥姆霍兹线圈在z-x平面的磁通密度模 (b) z轴亥姆霍兹线圈在y轴上的磁通密度模大小变化图6 z轴亥姆霍兹线圈的磁场仿真结果分析Fig.6 Analysis of magnetic field simulation results of z-axis Helmholtz coil

2.3 旋转磁场仿真分析

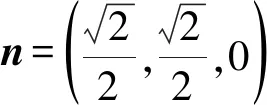
(11)

由式(6)可知，亥姆霍兹线圈所产生的磁场强度和通入线圈的电流成正比，且磁感应强度和电流的关系为:

(12)

式(11)和(12)联立，取B0=3 mT，f=1 Hz，得到通入线圈的电流表达式：

(13)

在COMSOL仿真软件中，对3组线圈分别输入式(13)的交变电流来进行组合线圈磁场的有限元仿真研究.

(c) t=0.50 s (d) t=0.75 s 图7 旋转磁场的旋转方向Fig.7 Rotation direction of rotating magnetic field

在坐标原点附近定义了一些特殊的域点探针研究旋转磁场均匀区域的范围.以x轴为例，在x轴的正半轴上定义了5个域点探针，域点探针的坐标分别为(0,0,0)、(0.05,0,0)、(0.1,0,0)、(0.15,0,0)、(0.2,0,0).当t=0s时，x坐标为0.1和0.15这两个域点探针所对应的磁通密度模变化较大，继续在x轴坐标上0.1到0.2的区间内以步长0.01定义域点探针来进一步确定磁场的均匀区域的范围.旋转磁场的磁通密度模在不同时刻会随着时间而产生变化，在对0、0.25、0.50、0.75 s这4个时间点磁场内的各个域点探针磁通密度模进行比较后，得到0 s和0.50 s、0.25 s和0.75 s时间点的各域点探针磁通密度模相等，各轴轴线上磁通密度模的值如表2所示.

表2 各轴轴线上的磁通密度模(mT)Tab.2 Magnetic flux density modulus (mT) on the axis of each shaft

2.4 实验结果分析

2.2节中在证明了每对亥姆霍兹线圈分别在x-y、y-z、z-x平面的一定区域内可以产生均匀磁场的基础上，根据环形线圈具有对称性，说明在三维空间内能够产生均匀磁场.

空间内某点的磁感应强度B(x,y,z)与坐标原点处的磁感应强度B(0,0,0)的相对偏差e为：

(14)

偏差越小代表均匀度越高.

从图8可以看出，0 s时，当|x|<0.14,|y|<0.13,|z|<0.15时，相对偏差e≤1%；0.25 s时，当|x|<0.2,|y|<0.2,|z|<0.16时，相对偏差e≤1%.对于旋转磁场来说，均匀区范围是不同时刻磁场均匀区共有的空间范围，且3组正交的亥姆霍兹线圈的旋转磁场的均匀区域由半径最小的y轴亥姆霍兹线圈决定.从图8可以看出，在任何时候，磁场在y<0.13区域均具有良好的均匀性，并且可以将组合线圈中心的24 cm×24 cm×24 cm的立方体区域视为均匀的磁场.

3 结论

通过对3组正交的亥姆霍兹线圈组成的磁驱动装置建立数学模型和有限元仿真分析，可以证明组合线圈磁场可以产生驱动机器人所需要的均匀磁场和旋转磁场.通过控制输入3组线圈的电流大小、频率、相位可以调节三维旋转磁场的磁场强度、旋转频率和旋转方向，因此可以按照微型磁纳米软体机器人的驱动需求调节旋转磁场，为接下来研究机器人的运动模式和运动轨迹提供了理论依据.本文验证了3组正交的亥姆霍兹线圈可以产生均匀磁场和旋转磁场，并求出组合线圈磁场可以驱动机器人的有效均匀区为磁场中心24 cm×24 cm×24 cm的正方体区域，但在实际应用中，还得根据机器人的驱动需求进一步优化组合线圈的尺寸和结构参数.