花生叶面积指数地面高光谱遥感估算模型研究

李军玲，李梦夏，李树岩*，田宏伟

（1.中国气象局 河南省农业气象保障与应用技术重点实验室，郑州 450003；2.河南省气象科学研究所，郑州 450003）

0 引 言

【研究意义】花生的用途非常广泛，包括油用、食用和深加工食品用等，并且发展花生产业符合供给侧结构性改革的需求。叶面积指数（LAI）与作物光合作用和蒸腾作用关系密切，是反映作物群体长势的重要指标[1-2]。掌握作物LAI 及其动态变化对于作物生长监测[3]和作物估产[4]等有重要意义。【研究进展】传统LAI 测量方法为手工测量，之后又有LAI 2200冠层分析仪进行测量，这些方法均只能获取离散点上的LAI 信息，难以获取大尺度、长时序数据，其有效性难以保障[5]。遥感监测技术具有大面积实时观测、客观性强和成本低等特点[6]，已被越来越多地应用在农业研究和生产管理中。高光谱遥感能够区分地物微弱光谱差异，在植被覆盖度、LAI、生物量、叶绿素、冠层含氮量等估算研究方面有明显优势[7-9]。刘轲等[10]研究表明，光谱分辨率较高的数据表现出更优的LAI反演精度与稳定性。很多研究利用植被指数进行LAI反演，针对高光谱遥感数据则专门提出了使用高光谱波段反射率计算的高光谱植被指数[11]，或利用波形分析技术构建的新型指数[12]。但不同的植被指数对不同因素和干扰的抵抗性有明显差异，因此对于LAI 反演需要找到最优植被指数。也有学者利用光谱特征边参量进行LAI 的估测，如红谷位置、红边位置[13]、红边峰值面积、红边振幅[14]、绿峰峰度[15]等。Herrmann等[16]利用红边特征估算小麦LAI，结果显示比NDVI估算LAI 更有效。另外还有学者认为和NDVI 相比，作物冠层的高光谱反射率及其导数等变换形式更适于LAI 反演[17-18]。以上这3 种基于植被指数、光谱特征边及光谱反射率的光谱特征参量各有优劣。陈江鲁等[19]分别利用这3 种光谱特征参量研究棉花冠层光谱对不同叶面积指数的响应，建立棉花叶面积指数光谱参数最佳估测模型。李军玲等[20]通过对高光谱数据进行不同形式的变换以及高光谱特征变量的计算，与叶面积指数进行相关分析，获得进行冬小麦不同生育期叶面积指数高光谱估测的敏感波段或指数。郭建彪等[21]对小麦LAI 和冠层光谱变化特点、估算模型及其品种间的差异等进行了系统分析，认为可以通过建立单品种模型来提高估算精度。【切入点】以往多是针对小麦、棉花进行的研究，很少有针对花生进行的LAI 估测研究。【拟解决的关键问题】为获得花生LAI最优估算模型，在原始光谱基础上进行了导数等变换，选取高光谱特征边变量和高光谱植被指数进行建模，并通过比较模型精度选择出最优估算模型；另外针对花生果实为地下果的实际情况，花生发育前期出苗期、幼苗期和后期成熟期叶面积指数并不能反映花生长势情况，因此选取花生结荚期—饱果期进行研究。

1 材料与方法

1.1 试验设计

试验于 2019 年在郑州市农业气象试验站（34°43′N，113°39′E，海拔111.3 m）进行，土壤类型为砂壤土，供试花生品种为豫花40。2019 年6 月5 日播种，株距10 cm，行距60 cm，常规管理。设置3 个不同氮素水平T1、T2、T3，施氮量分别为45、80、135 kg/hm2，每个处理设3 个重复，共9 个小区，每个小区2.7 m×4 m。在试验站内大田（0.067 hm2）选取2 个固定观测点作为对照。选取9 个小区的试验数据建立模型，选取2 个大田观测点数据对所建立的模型进行检验。

花生冠层光谱数据的测定应选择晴朗无云或少云的天气。因此，选择典型晴天分别于7 月2 日、13 日和22 日，8 月5 日、15 日和29 日，9 月6 日和20 日测定8 次光谱数据，并于同1 d 测定相应叶面积指数。

1.2 测量方法

1.2.1 花生冠层光谱测定

花生冠层光谱数据的采集使用便携式光谱仪ASD HandHeld 2（美国）进行，其波长范围325～1 075 nm，光谱采样间隔约1.5 nm。花生生长期内选择晴天，在10:00—13:00 之间测定。测点距冠层顶部垂直高度约1 m，每个小区随机选取5 个生长均匀且无病虫害的样本点进行测定，每个样本点测定5 次。

1.2.2 花生LAI 测定

使用LAI2200 冠层分析系统（美国）进行花生LAI 采集，测量日期和光谱采集日期相同，取5 个生长均匀且无病虫害的样本点测5 次求平均。

1.3 分析方法

首先使用ASD 光谱仪自带的ViewSpecPro 程序计算每个小区的光谱反射率。然后对原始光谱反射率进行倒数对数、一阶导数、二阶导数等不同形式变换，并进行高光谱特征变量的计算，在SPSS 数理统计软件中进行LAI 和光谱相关参数的相关分析。9 个小区测量数据作为训练样本建立叶面积指数与高光谱变量的拟合模型，2 处大田观测点测量数据作为验证样本，模型的模拟精度利用均方根误差（RMSE）进行评价[16-17]。

1）倒数对数、一阶导数和二阶导数的计算

整理并计算9 个小区和2 个大田观测点的花生冠层反射率数据，并计算其相应的倒数对数、一阶导数和二阶导数。

2）高光谱特征变量

选择基于高光谱面积变量、位置变量和植被指数变量3 种类型共20 个高光谱特征变量[13]（表2）。

3）模型构建及检验

以9 个小区测量数据为训练样本进行建模。首先进行高光谱特征变量[14-15]与LAI 的相关分析，选择出显著相关的光谱特征变量，利用这些变量建立LAI 单变量估算模型；再利用这些光谱特征变量进行多元逐步回归分析，建立LAI 的多元回归模型。

大田观测点数据作为验证样本，利用均方根误差（RMSE）和决定系数（R2）等统计指标评价LAI 估算模型精度。

2 结果与分析

2.1 花生生育期叶面积指数和光谱的变化特征

图1 为不同处理花生叶面积指数随时间的变化情况。由图1 可见，不同处理花生长势有较明显的差异，8 月29 日前差异明显，特别是T3 处理叶面积指数明显高于T1、T2 处理，T2 处理大部分时间都高于T1 处理，可能是T2 处理虽然比T1 处理氮素水平高，但T1、T2 处理的氮素水平仍不足以满足花生生长需要，T3 处理已经达到花生生长所需要的氮素水平。

9 月6 日之后，3 个处理叶面积指数相差不大，可能是花生生长后期叶面积指数已经不能反映出花生长势，对以后建立叶面积指数估算模型、利用模型结果反映花生长势等有一定的参考价值。图1 显示3个处理在7 月13 日和8 月5 日的叶面积指数差异最为明显，9 月6 日和20 日差异最小。

3 个处理在7 月13 日和9 月6 日花生冠层的光谱特征如图2。图2 显示叶面积指数差异明显的7 月13 日，冠层光谱反射率也存在显著差异，T1、T2 处理差异较小，但T3 处理和T1、T2 处理的差异较大；9月6日3 种处理的冠层光谱反射率也几乎没有差异。表明花生冠层光谱反射率可以揭示花生叶面积指数的差异，利用冠层光谱特征进行花生叶面积指数估算有一定的科学意义。

2.2 叶面积指数与冠层光谱的相关性分析

从图1 可以看出，9 月6 日和20 日花生成熟期叶面积指数已经不能反映花生长势，而7 月2 日和13 日由于处于花生生长早期，也难以反映花生后期长势和产量。因此选取7 月22 日，8 月5 日、15 日和29 日数据建立叶面积指数的估算模型。共9 个小区4 次观测36 组数据。导数变换可以减弱或消除背景、大气散射的影响，原始光谱的倒数对数可以有效反映地物的吸收特征[17]。故利用花生冠层高光谱反射率及其倒数对数、一阶导数和二阶导数与LAI 进行相关分析（图3）。

由图3 可见，在近红外波段范围内LAI 与原始光谱反射率正相关，在400～710 nm 的可见光范围内负相关，倒数对数光谱则相反。由图3 选择LAI 估算敏感波段，即662 nm 处倒数对数光谱、582 nm 处一阶导数光谱、753 nm 处二阶导数光谱，这些波段与LAI的相关系数均通过0.01 水平的显著性检验，且相关系数最大。

表1 花生冠层LAI 与高光谱变量间的关系Table 1 The correlation between peanut LAI and hyperspectral variables

2.3 叶面积指数与高光谱特征变量的相关性分析

计算LAI 与各高光谱变量间的相关系数（表1）。从表1 可以看出，LAI 与除蓝边位置、红边位置、绿峰反射率、SDr/SDy外的所有高光谱变量间的相关均通过0.05 水平的显著性检验。其中，LAI 与绿峰反射率和红谷反射率构成的植被指数VI1、VI2、SDy的相关系数绝对值大于0.70，除此之外LAI 与蓝边幅值、黄边位置、红边幅值、绿峰位置、红谷反射率、蓝边面积、红边面积、VI5、VI6之间的相关系数均通过0.01 水平的显著性检验。表明可以通过光谱变量来估算LAI，从而揭示花生的长势。故选取Db、λy、Dr、Rg、Rr、SDb、SDy、SDr、VI1、VI2、VI5、VI6作为模型自变量。

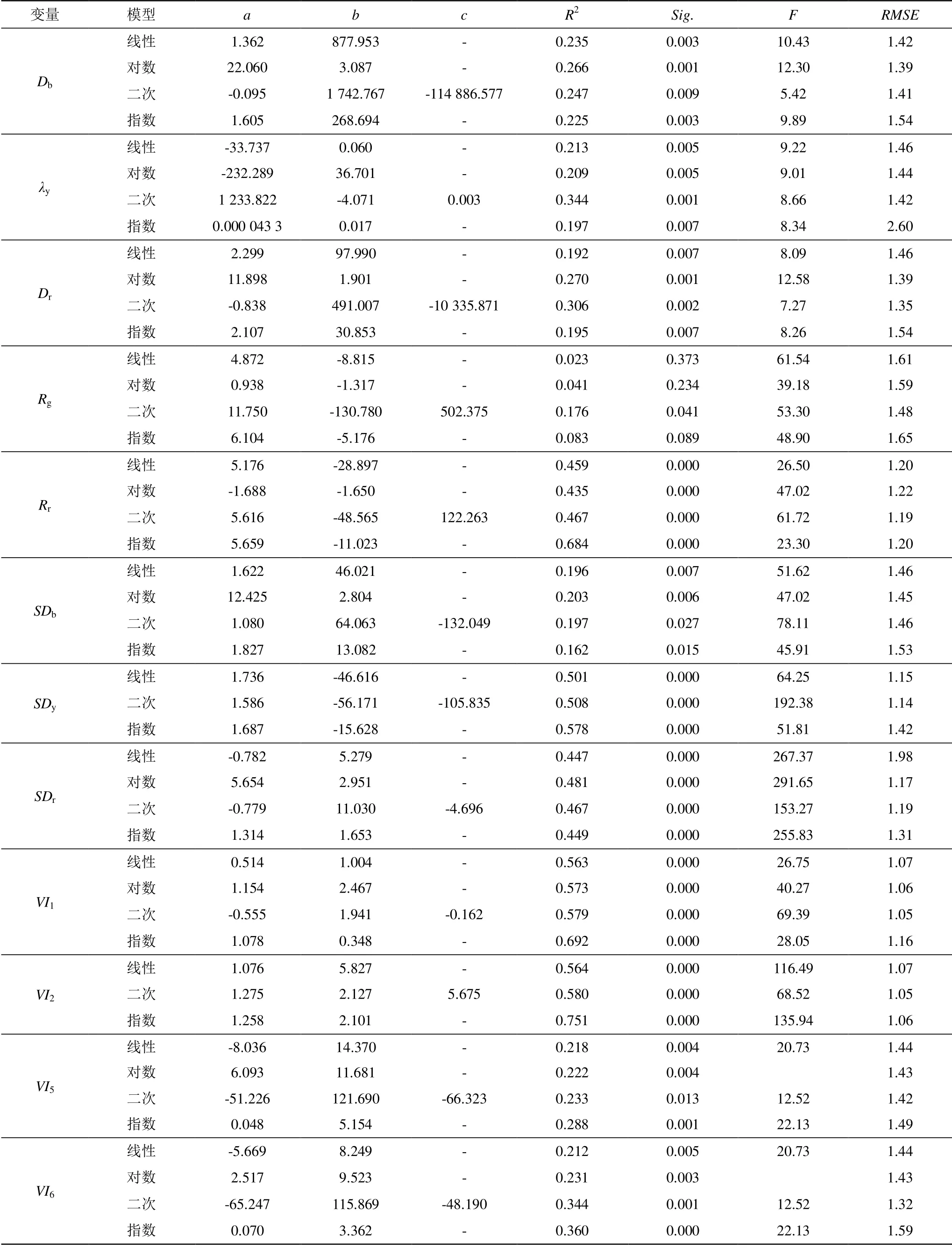
表2 花生冠层LAI 模型参数Table 2 Model parameters for LAI of peanut canopy

2.4 花生LAI 估算模型

2.4.1 单变量模型

基于2.3 节分析，选择波段662 nm 倒数对数光谱、波段582 nm 一阶导数光谱、波段753 nm 二阶导数光谱、Db、λy、Dr、Rg、Rr、SDb、SDy、SDr、VI1、VI2、VI5、VI6，建立单变量LAI 模型（表2），除Rg外方程均通过0.05 水平的显著性检验，其中Rr、SDy、SDr、VI1、VI2方程均通过0.01 水平的显著性检验，同时预测值的RMSE 相对较小。VI2的指数模型R2最大，为0.751，且RMSE 最小，为1.06。因此认为以VI2为自变量的指数模型为最优估算模型，其次为以VI1为自变量的指数模型。

因此，花生叶面积指数单变量最优模型为：

式中：y 为估算的LAI；x 为VI2。

2.4.2 LAI 估算的多元回归模型

作物叶片中不同生化物质都有其特定的光谱特征，仅用单一波段估测其物理或生化特征有其局限性，需要选择多个波段组合使用[19-20]。根据表1选择和LAI呈极显著相关的Db、λy、Dr、Rg、Rr、SDb、SDy、SDr、VI1、VI2、VI5、VI612个变量进行多元逐步回归分析，以9个小区测量数据作为训练样本构建LAI的多元回归模型，以2处大田观测点测量数据作为验证样本，利用均方根误差（RMSE）对模型进行验证。模型如下：

式中：y 为估算的LAI。该模型决定系数（R2）为0.813，大于单变量LAI 估算模型的决定系数，说明该模型拟合效果最好；均方根误差（RMSE）为0.702，小于单变量LAI 估算模型的均方根误差，说明其模拟精度优于单变量估算模型。

3 讨 论

利用高光谱遥感数据估算小麦、棉花和水稻的LAI 研究很多[18-21]，但针对花生的LAI 估算研究还不多见，在河南地区利用高光谱遥感估算花生冠层LAI的研究尚未见报道。本文设置不同氮素水平的花生试验，对花生冠层高光谱数据进行倒数对数、导数变换，并选取常见高光谱特征指数建立了花生LAI 估算模型，通过模型精度比较从中选择出最优估算模型。结果表明叶面积指数差异明显的时段，冠层光谱反射率也存在明显差异，叶面积指数差异不明显的时段，3种氮素处理的冠层光谱反射率也几乎没有差异。说明花生冠层光谱反射率可以揭示花生叶面积指数的差异，利用冠层光谱特征进行花生叶面积指数估算有一定的科学意义，有学者进行了相关研究[22-24]。基于此，对花生叶面积指数与冠层光谱及其变换形式进行了相关性分析。结果表明，花生LAI 与662 nm 处倒数对数光谱、582 nm 处一阶导数光谱、753 nm 处二阶导数光谱的相关系数均通过0.01 水平的显著性检验，且相关系数最大，吕晓等[23]研究认为花生LAI 和684 nm 处倒数对数光谱、793 nm 处一阶导数光谱的相关系数最大，和本文结果有一定差异，可能是因为试验分别在郑州和沈阳进行，水热条件差异较大导致。花生LAI 与蓝边幅值、黄边位置、红边幅值、绿峰位置、红谷反射率、黄边面积、红边面积、VI1、VI2、VI5、VI6之间的相关系数均通过0.01 水平的显著性检验，其中，LAI 与VI1、VI2及SDy的相关系数绝对值大于0.70，表明可以通过光谱变量变化来估算LAI，从而揭示花生的长势情况。利用筛选出来的敏感参数建模并验证后显示，以VI2（即绿峰反射率Rg与红谷反射率Rr的归一化指数）为自变量的指数模型最优。吕晓等[23]是利用敏感波段构建常用植被指数RVI、DVI、NDVI等进行花生LAI 的估算，张晓艳等[22]在花生结荚期-饱果期利用花生冠层反射光谱红边参数估算了花生LAI。本文考虑了更多的光谱特征参数和光谱植被指数，通过研究表明VI2相比红边参数有更高的模拟精度，也表明有从不同曲线特征进行高光谱位置、面积和植被指数变量分析的必要性，与只分析常用植被指数和单一特征参数相比，考虑得更加直接和全面[25-27]。

本文选择和花生LAI 呈极显著相关的Db、λy、Dr、Rg、Rr、SDb、SDy、SDr、VI1、VI2、VI5、VI612个变量进行了多元逐步回归分析，构建了LAI 的多元回归模型，并利用均方根误差（RMSE）对模型进行验证。多元回归模型决定系数（R2）明显大于单变量LAI 估算最优模型，均方根误差（RMSE）小于单变量LAI 估算最优模型，因此认为在光谱指数均能计算获取的基础上，应选择多元回归模型对花生LAI 进行计算。以往未见利用多元回归模型对花生LAI 进行估算的研究。李军玲等[20]证实了冬小麦分发育期建立LAI 估算模型的必要性。但对于花生而言，一是发育期更短；二是由于地下果的原因，导致发育后期叶面积指数难以反映花生长势的好坏；三是7 月中上旬花生处于生长早期，也难以反映花生后期长势和产量。因此，本文对7 月22 日—8 月29 日4 次观测数据进行建模发现，分2 个发育期和不分发育期的建模精度差别不大。因此对于花生而言，选择能够反映花生长势的观测日期比分发育期更重要。但也可能是本文用了1 年试验数据，样本有限，今后将继续进行相关试验，在对模型不断进行验证和改进的同时，进行更多时次的观测研究分发育期建模是否必要，同时对比单变量估算模型和多元回归模型的优劣。

4 结 论

1）花生LAI 估算的敏感波段为662 nm 处倒数对数光谱、582 nm 处一阶导数光谱、753 nm 处二阶导数光谱。

2）花生LAI 估算的敏感参数为Db、λy、Dr、Rg、Rr、SDb、SDy、SDr、VI1、VI2、VI5、VI612 个变量。可以通过VI2（即绿峰反射率Rg与红谷反射率Rr的归一化指数）变量来估算LAI，从而揭示花生的长势。

3）选择和花生LAI 呈极显著相关的12 个敏感参数进行多元逐步回归分析，构建花生LAI 的多元回归模型，其模拟精度优于单变量估算模型，认为多种光谱参数均可获取的情况下，优先选用多元回归模型对花生冠层LAI 进行估算。