光纤直流大电流传感器非线性机理及校准技术

李 奇，李传生，梁 波，蔡晋辉，邵海明，梅国健

(1.中国计量大学，浙江 杭州 310018；2.中国计量科学研究院，北京 100029)

1 引 言

在冶金工业，铝、铜、铅、锌、镁等产品需要通过直流电解的方法分解产生，电解电流从几kA到数百kA，大型电解铝厂的整流系统直流电流已高达300 kA以上。直流超大电流的精确测量对于过程控制、设备保护以及节能降耗都至关重要[1,2]。

目前，金属电解直流超大电流的测量普遍采用霍尔电流传感器。测量精度受杂散磁场影响，体积与重量庞大,安装运输不便,难于校准等是此类传感器应用中存在的主要问题。基于Faraday磁光效应的干涉式光纤电流传感器具有测量精度高、动态范围大、测量精度对杂散磁场的敏感度低、便携性好、安装方便等优点，是直流超大电流测量的理想方案[3～5]。ABB公司于2007年成功研制了应用于电解冶金的光纤电流传感器[6,7]，是干涉型光纤电流传感技术在直流超大电流测量领域的首次成功应用。2012年，贾明等提出了一种开合式的光纤电流传感器敏感环结构[8]，解决了不断开载流母线情况下实现传感器敏感环在线安装的技术难题。目前，国内已有多家企业都具备了光纤直流超大电流传感器的研发和生产能力。笔者在对相关企业生产的和自行研制的光纤直流大电流传感器进行校准时，发现这些传感器普遍存在较大的非线性误差。

干涉型光纤电流传感器采用数字闭环信号检测技术，被测电流产生的Faraday相移被实时的反馈补偿，系统始终被锁定在灵敏度最高的90°工作点上，理论上可以在很大动态范围内保持较高的线性度[9～13]。但是，由于光纤1/4波片存在方位角及相位延迟误差，进入传感光纤的是两束正交的椭圆偏振光，它们将进一步在光路系统中演化成两束主波和两束幅值较小的次波。由次波干涉形成的寄生干涉信号与主波形成的干涉信号共同参与闭环检测，此时传感器的输出除与被测电流有关外，还与寄生干涉信号的幅值有关，传感器的输出随被测电流呈现非线性变化。

本文首先介绍了光纤电流传感器的工作原理；然后着重分析了传感器大电流测量非线性的产生机理，并对非线性误差进行了线性插值补偿；最后，利用直流超大电流校准装置进行了实验验证。

2 工作原理

光纤电流传感器的主要工作原理是基于Faraday磁光效应以及安培环路定理，即闭合传感光纤环路中的两束正交圆偏振光在被测电流的作用下产生与穿过环路的电流成正比的相位差。工作原理示意图如图1所示。

图1 干涉型数字闭环光纤电流传感器原理示意图Fig.1 Configuration of interferometric-type digital closed-loop fiber-optic current sensor

光源发出的光经环行器由起偏器变为线偏振光，经45°光纤熔接点进入保偏光纤的快轴和慢轴，并由1/4波片变为左旋、右旋圆偏振光，在被测电流的作用下产生相位差，之后经传感光纤末端反射镜反射，沿原路返回，相位差加倍：

φs=4F=4VNI

(1)

式中：F为Faraday相移；V为传感光纤的Verdet常数(V=1.02 μrad/A@1.31 μm)；N为光纤圈数；I为被测电流。两束正交的圆偏振光经1/4波片再次变为正交的线偏振光，但偏振方向发生互换。两束线偏正光经偏振器检偏，并发生干涉，干涉光强由光电探测器变为电信号，经前置放大、A/D转换变为数字信号，进行闭环信号处理。

闭环检测系统在相位调制器上施加方波和阶梯波调制信号。方波调制交替引入±π/2的调制相位，保证系统时刻工作在最高灵敏度上；阶梯波调制实时引入与被测电流产生的Faraday相移大小相等、符号相反的反馈相移，使系统始终锁定在π/2工作点，避免余弦函数周期多值的影响，提高传感器的线性度和动态范围。

3 非线性机理及校准技术

3.1 光路模型

系统中各光学器件的琼斯矩阵模型如下：

(1) 起偏器

(2)

Lpout=Lpin为光波反向通过时起偏器的琼斯矩阵。

(2) 45°熔点

(3)

(3) 直波导相位调制器

(4)

(4) 保偏延迟光纤

(5)

式中：βx、βy分别为保偏延迟光纤慢轴、快轴的传播常数；L为延迟光纤长度。Ldout=Ldin为光波反向通过时保偏延迟光纤的琼斯矩阵。

(5) 光纤1/4波片

(6)

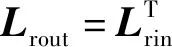
(6) 敏感环路

(7)

式中Lfout=Lfin为光波反向通过时敏感环路的琼斯矩阵。

(7) 反射镜

(8)

光路系统输出光波的琼斯矢量为：

Eout=Lpout·Lθout·Lmout·Ldout·Lrout·Lfout·Lrm·

Lfin·Lrin·Ldin·Lmin·Lθin·Lpin·Ein

(9)

式中：Ein为光源输出光波的琼斯矢量。干涉光强为：

(10)

将式(2)～(9)代入式(10)可以得到干涉光强的交流分量为：

2(1-sin22θsin2δ)cos(φm)+

(1-sin 2θsinδ)2cos(φm+4F)

(11)

式中：φm=φTM(t+τ)+φTE(t)-φTM(t)-φTE(t+τ)；α为光路损耗；P0为光源输出功率。

当系统闭环稳定时，数字闭环检测系统检测到的相位差为：

(12)

3.2 非线性误差仿真分析

由式(12)可以得出：光纤1/4波片相位延迟角度与方位角存在的角度误差是造成传感器非线性误差的原因。波片制作过程中不可避免地存在方位角误差与相位延迟角度误差，使得保偏光纤中的线偏振光被转化为椭圆偏振光，该椭圆偏振光可以分解为左旋圆偏振光与右旋圆偏振光；这就相当于在一种旋向的圆偏振光中耦合了少量另一种旋向的圆偏振光，从而产生误差，使得光纤电流传感器存在非线性的现象。

取点(I0，φs(I0))作为修正基准点，其中φs(I0)为数字闭环系统在电流为I0时检测到的相位差，则传感器的比例因子为：

(13)

此时，任意电流下传感器测量误差为：

(14)

取I0=240 kA，根据式(12)和式(14)，在不同的方位角和相位延迟误差下，对传感器测量误差与被测电流之间的关系进行仿真计算，结果如图2所示。随着光纤1/4波片相位延迟角度误差以及方位角误差增大，传感器测量误差也随之增大。

图2 光纤直流大电流传感器非线性误差仿真结果Fig.2 Nonlinear error of fiber-optic DC high current sensor caused by the imperfect retarder

对于相位延迟角度δ来说，当其误差在(90±6.40)°范围内，传感器测量误差优于±0.1%，为了控制传感器测量误差小于0.2%，光纤1/4波片相位延迟角度误差应控制在(90±9.05)°范围内；对于方位角θ来说，当其误差在(45±3.21)°范围内，传感器测量误差优于±0.1%，当其误差在(45±4.53)°范围内，传感器测量误差优于±0.2%。

在光纤1/4波片制作过程中，方位角的控制主要通过光纤熔接过程中精确调节对轴并监测消光比来实现。消光比一般可控制在0.5 dB以内，相应的误差约为±0.81°，造成的非线性误差仅为±0.006 7%，其影响可以忽略不计。但波片的相位延迟角度的误差控制则相当困难。首先，光纤1/4波片的长度通常仅为2～3 mm，当相位延迟角度精细调节时，需要调整的光纤长度仅有百分之几毫米，精确控制难度较大；其次，由于光纤制造工艺的缺陷，光纤的局部拍长并不均匀，这将导致相同长度的波片会有不同的相位延迟；另外，在光纤熔接过程中，电极放电过程也会对拍长产生影响，因此光纤1/4波片相位延迟角度的误差很难精确控制[14,15]。为了解决该问题，引入一种工程上非常有效的非线性补偿方法：分段线性插值补偿。

3.3 分段线性插值补偿方法

对传感器的误差进行实测，并以0.1%误差为间隔选取若干测试点(I1，e1)、(I2，e2)…(In，en)，分别在相邻两点做线性插值计算区间内不同电流下的测量误差，插值方程为相邻两点连线的直线方程，即：

en=k(n-1,n)·I+b(n-1,n)I∈[In-1,In]

(15)

式中k(n-1,n)、b(n-1,n)分别为直线的斜率和截距。修正后，传感器电流输出值为：

Iout=I×(1-en)

(16)

将式(15)代入式(16)，得到线性插值误差补偿算法为：

Iout=I×[1-(k(n-1，n)·I+b(n-1，n))]

(17)

该算法通过FPGA实现，式(17)中k(n-1,n)、b(n-1,n)通常为小数，需将其扩展为整数，即：

(18)

式中[*]表示取整运算，M的取值应保证k(n-1,n)、b(n-1,n)转换为整数后舍入误差尽可能小。式(18)可通过调用FPGA的乘法器IP核实现。

4 实验验证

4.1 实验装置

图3所示为光纤直流大电流传感器校准装置，采用等安匝法对传感器进行校准。大功率直流电源驱动4组串联等安匝母线，每组15匝，共计60匝，单匝通流能力可达5 000 A。电源产生2 500 A直流电流，传感光纤围绕母线绕制2圈，等效电流为300 kA。直流电流比较仪作为标准电流传感器，比例为6 000 A/10 V，准确度优于0.01%；6位半数字电压表(Keysight 34 465 A)测量标准电流传感器的输出电压。误差同步测量装置同步比较光纤电流传感器和标准电流传感器采样值的平均值，数据平均时间为200 ms，并计算测量误差。

图3 光纤直流大电流传感器校准装置Fig.3 Calibration device for fiber-optic DC high current sensor

4.2 补偿实验

分别制作3种不同长度的光纤1/4波片，依次集成于同一台光纤电流传感器样机中，并进行实验测试。在300 kA量程范围内选取14个测量点，分别测量了补偿前、后的传感器误差，结果如图4所示。

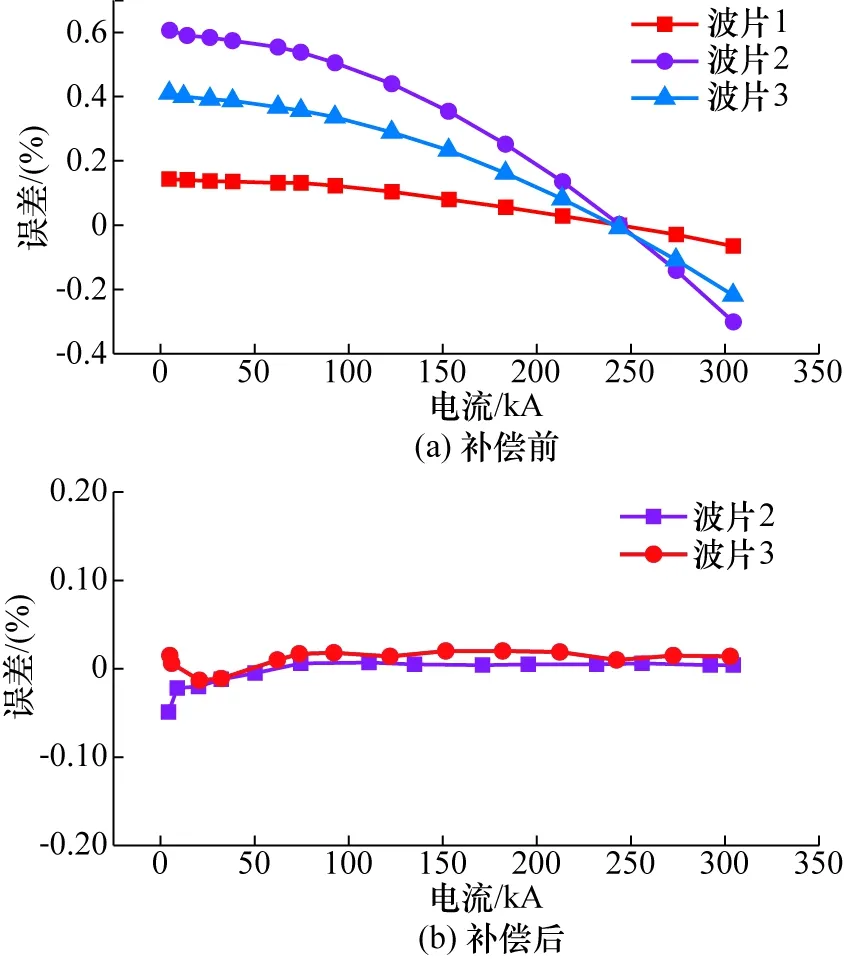
图4 不同1/4波片下光纤直流大电流传感器样机补偿前后误差曲线Fig.4 Error of fiber-optic DC high current sensor with different quarter-wave retarder

从图4可以看到：采用数字闭环测量方案的干涉型光纤电流传感器在测量直流超大电流时存在非线性误差，且随着被测电流的增大，该非线性越明显，实测结果与理论仿真趋势基本一致，说明光纤1/4波片相位延迟角度误差是导致光纤电流传感器超大电流测量非线性的主要原因之一。3组测试中，仅有1组测量误差在0.2%以内，另外2组的最大误差高达0.4%和0.6%。对测量实验中误差较大的2组传感器进行非线性误差补偿，补偿后测量误差均降至0.1%以内，证明误差补偿方法有效可行。

4.3 重复性实验

分别在5、300 kA时，对修正后的一台传感器进行10次重复性试验，假设误差符合正态分布，以误差均值作为最佳估计值，由贝塞尔公式得到误差的标准偏差σ如表1所示。

表1 传感器一重复性试验数据(安装波片2)Tab.1 Repetitive test data of sensor 1(mounting wave plate 2)

可以看出，受信噪比影响，电流较小时，传感器标准偏差较大。后期将进一步提高传感器信噪比，提高光纤直流大电流传感器测量性能。

5 结 论

围绕光纤直流大电流传感器的非线性误差机理和校准方法，开展了理论分析、仿真计算和实验验证工作，得到以下结论：

(1) 基于闭环信号检测技术的干涉型光纤电流传感器存在非线性误差，被测电流越大，非线性越明显。

(2) 光纤1/4波片的制作误差是导致光纤电流传感器非线性的主要原因之一。在现有技术工艺下，波片相位延迟误差的影响较大，为保证最大误差小于0.2%，相位延迟误差应在±9.05°以内；方位角误差的影响基本可忽略。

(3) 分段线性插值补偿方法可有效改善光纤直流大电流传感器的非线性误差。在5～300 kA范围内，补偿后传感器样机的测量误差优于±0.1%。