振动条件下的尼龙拉链厚度尺寸视觉在线测量算法

2021-06-04 07:20洪涛，程诚

计量学报 2021年4期

洪涛，程诚

(中国计量大学质量与安全工程学院，浙江杭州 310018)

1 引言

尼龙拉链作为最常用的拉链产品，其厚度尺寸是评价尼龙拉链质量好坏的重要依据之一。随着智能制造模式在拉链产业的不断推进，在线视觉测量技术正逐渐取代了传统的人工测量方法，被广泛运用于拉链制造过程的质量控制[1,2]。对于尼龙拉链在成型过程中厚度的视觉测量，由于尼龙拉链自身的弹性特性，生产设备的振动状态会导致被测拉链的自身振动[3]，引起被测拉链各部分在图像中的坐标值发生偏移，这种偏移将会影响视觉测量结果的准确性。因此，研究振动条件下的尼龙拉链厚度尺寸的视觉测量算法，保证测量结果的准确性，对拉链质量控制具有重要意义。

在工件尺寸视觉在线测量过程中，为了消除被测物体自身振动对测量结果准确性的影响，可采用对拍摄到的图像进行运动补偿的方法，找出被测物体在不同时间段的相对位移关系，并对偏移进行补偿。近年来，很多学者在振动偏移量的视觉测量方面进行了诸多研究。利用结构光测量法[4,5]对振动偏移量实现高精度测量，但需要添加辅助的结构光投射器，在应用方面具有限制性；通过数字图像相关法[6,7]进行振动偏移量测量，利用数字散斑图像，可以大范围测量物体的三维全场振动信息，但需要进行大量的匹配计算，耗时较长且对计算机系统和相机要求较高；利用光流法进行振动偏移量测量[8,9]，能够实现对目标振动偏移量的快速测量且能保持一定的测量精度，但其结果为相邻帧之间的偏移量信息，无法根据该信息还原被测物体在无振动状态下的图像信息。

本文以尼龙拉链厚度尺寸在线视觉测量系统为研究对象，从拉链振动的机理分析和振动信息测量方法研究两方面入手，结合拉链横向振动模型及光流法原理，计算出拉链在某一时刻的全局振动信息。根据此振动信息，设计对应的运动补偿算法，并提出了相应的拉链厚度尺寸在线测量算法。

2 拉链厚度尺寸在线检测及问题分析

2.1 在线视觉测量系统设计

拉链厚度尺寸在线视觉测量系统主要包括图像采集单元、信号传递与控制单元、人机交互单元等。为了杜绝或减少外部环境对检测过程的影响，图像采集装置为一个封闭式壳体，其内部结构如图1所示。

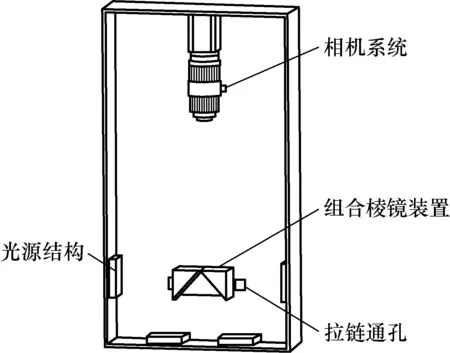
图1 图像采集装置内部结构图Fig.1 Internal structure diagram of image acquisition device

该图像采集装置主要由相机系统、组合棱镜装置、光源结构及拉链通孔4部分组成。其中，相机系统包括CCD工业相机与镜头，选用的相机型号为Basler acA1600-20gm GigE，相机的分辨率为1 626×1 236 pixel，20帧/s，像元尺寸4.4 μm；选用镜头的型号为Computar MP3514-MP2，35 mm固定焦距。组合棱镜装置由2个全反射直角棱镜组成，用于同时采集成型机中2条单边拉链的厚度图像。光源结构包括背光光源和光源连接机构，光源采用50 mm×50 mm的面状蓝色LED光源，光源通过光源连接机构固定在图像采集装置外壳的左右两侧。图像采集过程中，拉链通过拉链通孔穿过图像采集装置，其图像采集光路示意图如图2所示；采集到的拉链厚度图像如图3所示。

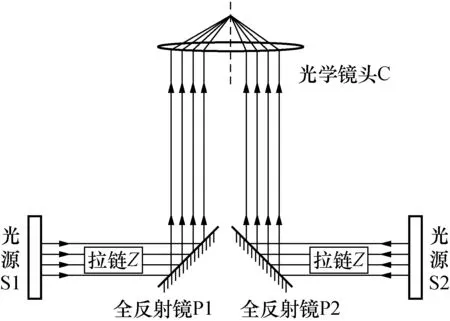
图2 光路示意图Fig.2 Schematic diagram of light path

图3 拉链厚度图像Fig.3 The collect images of nylon zipper’s thickness

2.2 在线测量过程中的振动分析

在拉链厚度尺寸在线测量过程中，被测拉链的振动主要来源于拉链成型机的电动机工作振动，经过系统的各个部件将振动传递到拉链限位装置而引起振动。由于尼龙拉链属于粘弹性材料，振动具有迟滞性，无法与限位装置保持振动一致，从而造成拉链自身的横向振动。

根据图2拉链成像光路示意图可得，拉链成像过程中，光轴变化示意图如图4所示。

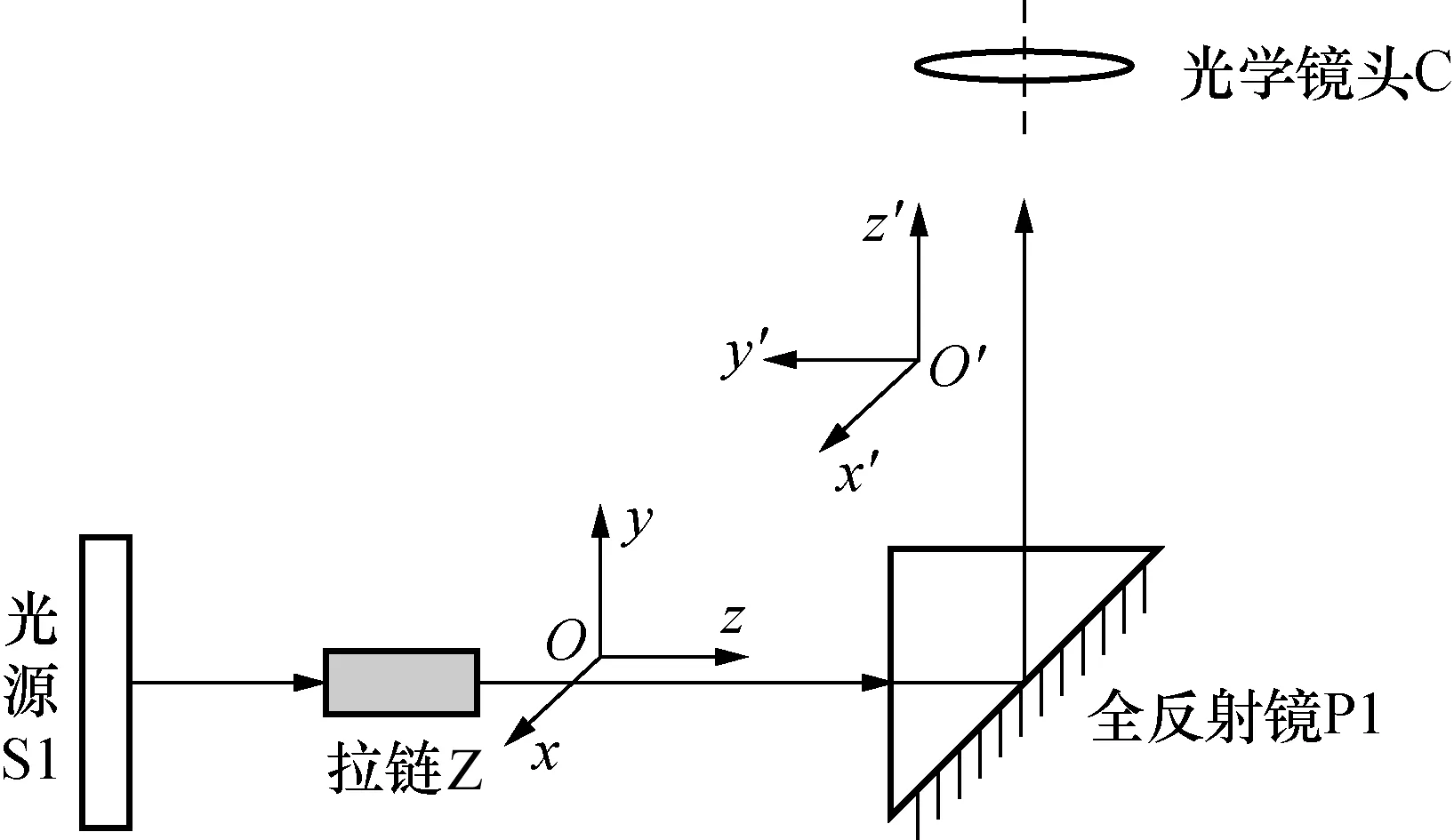
图4 光轴变化示意图Fig.4 Schematic diagram of optical axis change

图4中，三维坐标系O-xyz为输入坐标系；三维坐标系O′-x′y′z′为输出坐标系。由图4可知，在测量拉链厚度尺寸时，拉链的自身振动即拉链相对于Oy轴平移，会引起成像相对于O′y′轴的平移，即成像相对于无振动状态下的位置向左或向右的变化，表明被测拉链各部分在图像中的坐标点发生左右偏移。因此需要引入对拉链的横向振动模型的研究，通过研究结果对拉链厚度尺寸测量结果进行运动补偿，减少拉链自身振动对视觉测量结果的影响。

3 拉链全局振动信息的计算

3.1 拉链横向振动模型研究

由于拉链成型机上的升降装置的作用，拉链在经过采集装置时，会在一段时间保持运动,一段时间保持静止。而拉链实际生产速率仅为0.06 m/s，所以暂不考虑轴向运动速率对拉链轴向振动产生的影响。

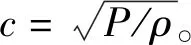
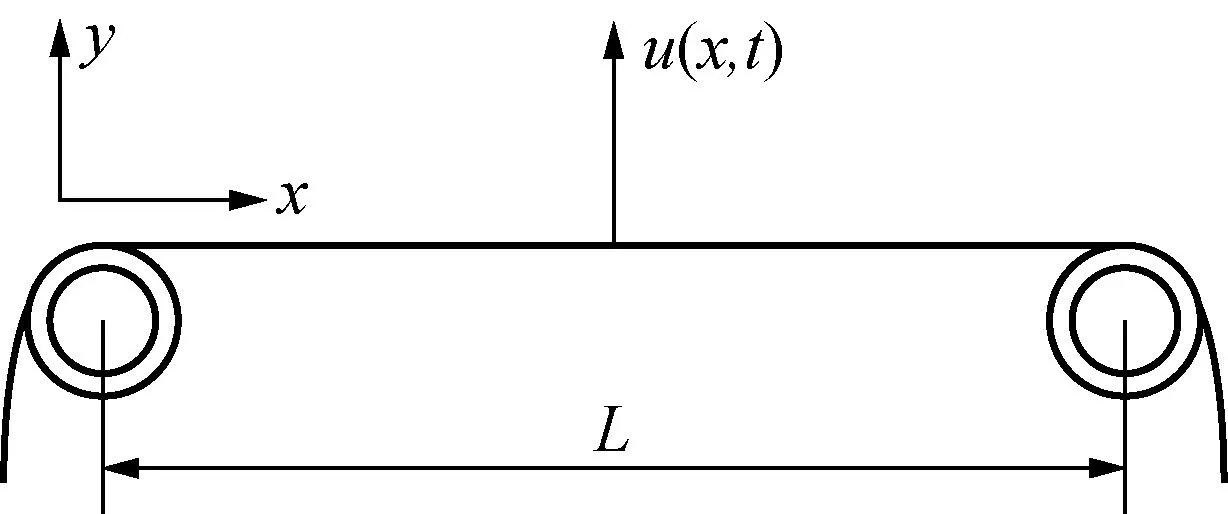
图5 拉链简化模型Fig.5 The simplified model of nylon zipper

设拉链的张力保持不变，在激励源的作用下做微小横向振动。若忽略其它外力的影响，利用Hamilton原理，参考Wickert和Mote建立轴向运动弦线横向振动运动微分方程的方法[10]，建立拉链横向振动模型的微分方程如下：

(1)

采用分离变量法[11]对式(1)求解，可以得到z轴方向上的拉链横向振动u(x,t)的级数解。

(2)

式中：n为弦的波数，m为无穷级数的项数。

根据式(2)可计算出在相邻两帧时间t1、t2之间，被测拉链在x=L/2处的横向振幅变化值Δu的表达式：

cos(ωt1) sin(ωΔt)]=Bsin(ωt1+θ)

(3)

式中：Δt为t1、t2的时间间隔；

3.2 基于光流法的拉链全局振动信息计算

LK(Lucas Kanade)光流法是一种广泛使用的光流估计差分方法，利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系，从而计算出相邻帧之间物体的运动信息[12]。

设I(x,y,t)是图像像素点(x,y)在时刻t的灰度值，根据光流法的基本假设，有：

I(x,y,t)=I(x+dx,y+dy,t+dt)

(4)

将上式右端进行泰勒展开，并化简可得光流约束方程：

Ixux+Iyuy+It=0

通过LK光流法求解光流约束方程，解得图像的光流信息如下：

(6)

通过LK光流法计算得到被测拉链相邻两帧t1、t2在中点附近区域的光流信息图，如图6所示，图6中白色箭头短线即为计算得到的光流信息。

图6 光流信息图Fig.6 The infographic of optical flow

由此可提取出相邻两帧时间t1、t2之间，被测拉链在x=L/2处的实际横向振幅变化值uym。令Δu=uym可解得：

(7)

由于拉链振动为周期性变化，所以求解出的t1在单个振动周期内的对应结果存在两种可能情况。因而将t1代入式(2)所求得的t1时刻被测拉链的横向振动幅值，即被测拉链的全局振动信息也存在对应的两种结果，分别为式(9)和式(10)。

(9)

(10)

因此通过设定判定准则，选择出t1时刻被测拉链的实际全局振动信息，具体的操作步骤将在第4.3节中的运动补偿算法中进行详细描述。

4 拉链厚度尺寸在线测量算法设计

4.1 测量算法总体流程设计

基于图像运动补偿的拉链厚度尺寸在线测量算法流程图如图7所示。图7中，左侧虚线框内为特征提取算法的具体步骤；右侧虚线框内为运动补偿算法的具体步骤。

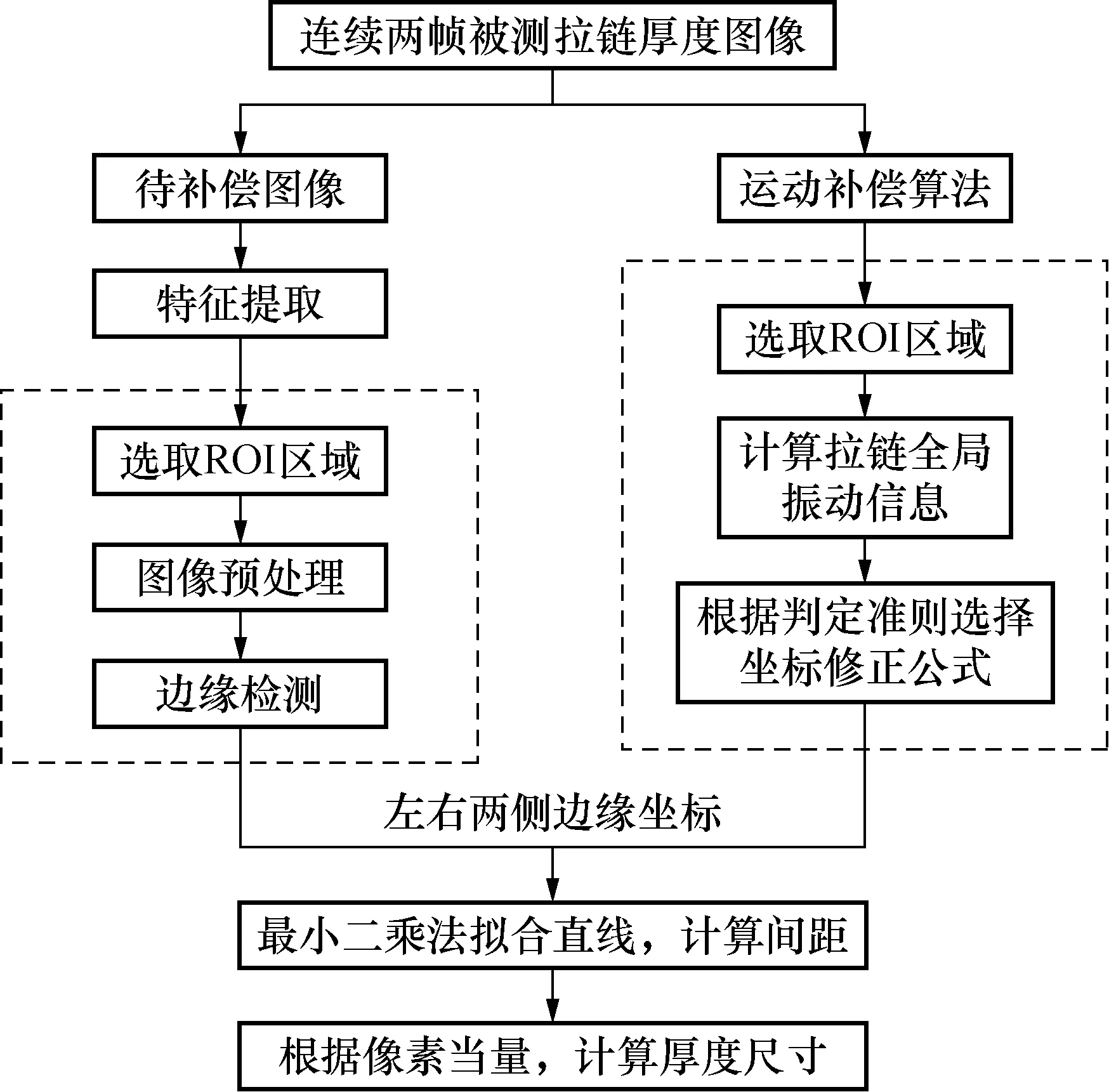
图7 拉链厚度尺寸在线测量算法流程图Fig.7 Flow chart of online measurement algorithm for zipper’s thickness dimension

首先输入连续两帧被测拉链的厚度尺寸测量图像；然后，选取t1时刻的图像作为待补偿图像，利用特征提取[13]算法，提取出图像中被测拉链左右两侧的边缘点坐标；与此同时，利用运动补偿算法，计算坐标修正公式，接着对提取出的边缘点坐标进行修正；然后通过最小二乘法[14]将修正后的边缘点坐标拟合成直线，并计算这两条拟合直线的间距；最后根据标准件计算出的像素当量[15]，将间距转换为拉链厚度的实际尺寸。

4.2 特征提取

4.2.1 选取ROI区域

感兴趣区域(region of interest，ROI)是从被处理的图像中以多种方式提取出所需要处理的区域。通过分析拉链的成像特征可知，采集到的图像中存在左右2条单边拉链，因此需选取2个ROI区域，将2条单边拉链的检测区域分别提取出来，以保证后续图像处理时获得足够的信息。选定的ROI如图8所示。

图8 拉链ROI选定图像Fig.8 The ROI selected image of nylon zipper

4.2.2 图像预处理

为将拉链待测目标区域图像从背景中提取出来，需对图像进行图像预处理，包括图像滤波、阈值分割等操作。本文使用中值滤波、类间方差法进行图像预处理，将拉链待测目标区域图像提取出来，图像预处理结果如图9所示。

图9 图像预处理结果Fig.9 Image preprocessing result

4.2.3 边缘检测

本文利用投影法结合扫描法提取边缘点位置，算法流程图如图10所示。

图10 边缘检测算法流程图Fig.10 Flow chart of edge detection algorithm

(1) 以拉链单厚的二值图像的上端作为起点，选定一个初始子ROI区域，水平宽度保持不变，竖直方向上长度变为拉链两齿头标准间距为Δd，保证子ROI区域内仅有一个拉链齿头；

(2) 在此子ROI区域内，首先通过垂直投影法，计算得到一个(1×l)的一维数组；

(11)

(3) 从数组左侧开始，依次读取数组中的数值并进行判定：当第α-1个数值为0，而第α个数值发生变化，不为0时，此时α的值为对应被测拉链厚度的左侧边缘y轴向坐标yl；

(4) 接着从数组右侧开始依次读取数值判定：当第l-α个数值为0，而第l-α+1个数值发生变化时，认定此时l-α+1的值为对应被测拉链厚度的右侧边缘y轴向坐标yr；

(5) 然后分别依次读取yl,yr列中每行对应像素点的像素值，当像素值等于1时，记下该点行号，即为x轴坐标向xl,xr，由此得到坐标(xl,yl)，(xr,yr)；

(6) 根据得到的坐标值，以(xl+xr)/2为起点，在间隔Δd距离处，选取一个长度为齿头标准尺寸dc，水平宽度与原ROI宽度相同大小的ROI区域；

(7) 重复(2)至(6)直至无法选取一个完整的子ROI区域，循环结束，并将所获得的坐标转换成原图像上的对应坐标。

由此将ROI区域划分为多个仅包含单个链头的子ROI区域，并确定左右两侧的边缘点坐标。

4.3 运动补偿算法

根据第3.2节可知，t1时刻被测拉链会求解出两个不同的拉链全局振动信息，与实际状态不符。因此本文提出一个判定准则，用于选择被测拉链实际振动信息所对应振动幅值表达式。结合判定准则提出运动补偿算法。具体步骤如下：

(1) 首先通过选取ROI区域，设定左右两条单边拉链的检测范围，并读取对应的中点坐标(xmid,ymid)；

(2) 将采集到的相邻两帧图像的时间设为t1和t2，利用上文所述的基于光流法的拉链横向振幅计算算法，可拉链中点处的横向振幅变化值，计算出t1时刻拉链的横向振动幅值的表达式u1(x,t1)和u2(x,t1)；

(3) 接着根据边缘检测算法，计算出拉链中点处对应子ROI区域(仅包含单个链头)内的左右两侧边缘点坐标(xl,yl),(xr,yr)；

(6) 根据步骤(5)所得的修正公式对各个子ROI区域左右两侧的边缘点坐标进行运动补偿，确定最终的边缘点坐标。

4.4 最小二乘法拟合直线

本文利用整体最小二乘法[14,15]拟合关于拉链厚度的左右两侧边缘直线。整体最小二乘法其实质为边缘点到拟合直线的正交距离的平方和最小。

由于需要保证拟合出的2条直线是平行线，本文对全局最小二乘法进行了改进。设2条拟合直线Ll和Lr的方程为式(12)，根据拟合准则式(13)，求出2条拟合直线。

Ll：yl=axl+bl
Lr：yr=axr+br

(12)

(13)

式中：k为边缘点个数；xli、yli、xri、yri为直线Ll、Lr的第i个边缘点的横坐标和纵坐标；a为直线斜率；bl、br为直线Ll和Lr的截距。

然后根据式(14)求出两直线的间距即拉链厚度尺寸dl-r。

(14)

4.5 拉链厚度尺寸计算

最小二乘拟合所得的拉链厚度尺寸大小都是以像素为单位的，所以需要用标准拉链进行标定[16]，根据实际值长度单位(mm)与像素单位(pixel)之间的像素当量K，将拉链像素尺寸dl-r转换为实际尺寸da。

da=K×dl-r

(15)

5 实验结果与分析

本文系统软件环境基于LabVIEW 8.5和MS SQL Sever 2000，结合NI Vision的图像处理函数库进行算法验证。实验材料为N7反装型尼龙拉链，该拉链的厚度成型尺寸标准为(2.22±0.01)mm。相关实验参数设置为：K=0.022 94，m=20，Δt=0.05 s。利用加速度传感器获取滑轮的振动信号分析可得激励源参数：A=0.49 pixel，ω=85.408 rad/s。

首先，将尼龙拉链厚度尺寸在线视觉测量系统安装在正常工作的成型机上，实验样本按实际生产速度运动，使用本文设计的测量算法测量样品10次；然后使用无运动补偿的视觉测量方法对这10个位置进行测量，每个位置重复测量3次，测量结果取平均值，对比2种方法的测量结果以测量结果的不确定度U作为评价指标。其测量结果如表1所示。

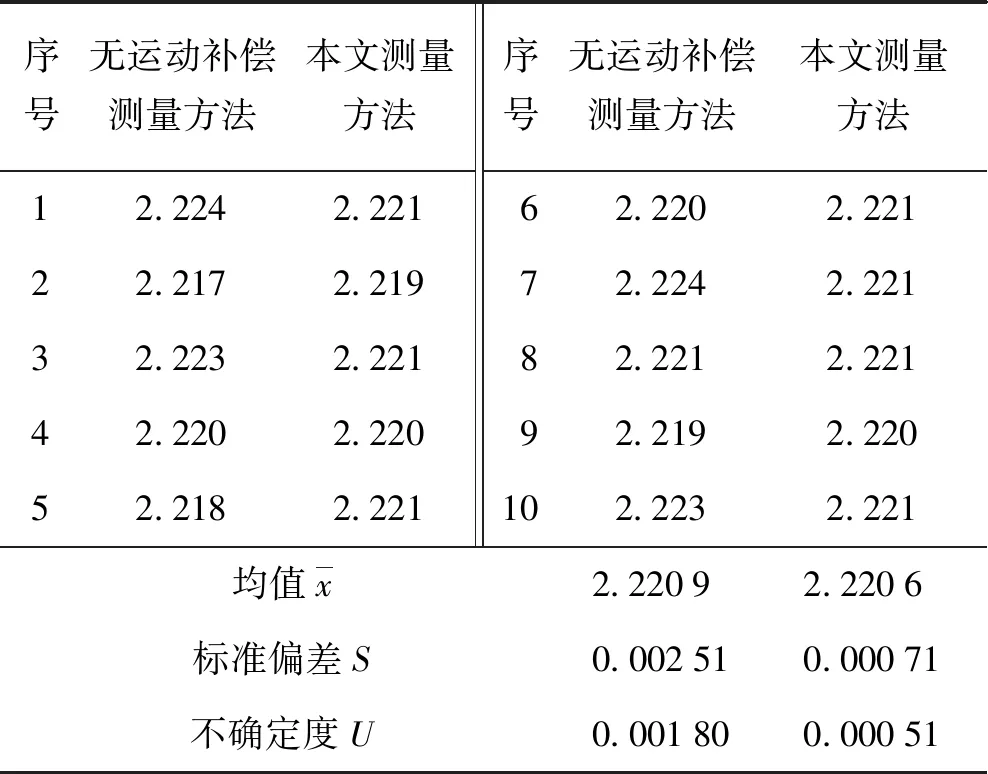
表1 测量结果对比Tab.1 Comparison of measurements mm

(16)

(17)

式中：N为测量次数;xj为测量值;tp为扩展倍数，与测量次数与置信率有关,本文中选取置信率为95%，则tp为2.26。

根据拉链检测技术要求，厚度尺寸测量结果的不确定度要求应满足U≤0.001 mm。

由表1可知，使用无运动补偿的视觉测量方法所测得拉链厚度尺寸结果的测量不确定度U为0.001 80 mm，无法满足技术要求。而本文所提出的测量方法测量结果的不确定度U仅为0.000 51 mm，从而满足拉链实际检测技术要求。

6 结论

针对在拉链厚度尺寸在线视觉测量过程中，由于尼龙拉链其自身的弹性特性，受到生产设备的振动状态影响会产生的自身振动，从而对视觉测量系统的准确性造成影响的问题，本文提出了一种振动条件下的尼龙拉链厚度尺寸的在线测量算法，添加了对振动偏移量进行修正的运动补偿算法，降低了拉链自身振动对测量结果的影响。实验结果表明：本文测量方法，测量结果的不确定度为0.0005 1 mm，实现了尼龙拉链厚度尺寸的高精度在线视觉测量，具有较好的工业应用价值。