迭代混合实验收敛速度与收敛精度的数值模拟
王 涛,郑 欢,王 贞,许国山
(1.黑龙江科技大学 建筑工程学院, 哈尔滨 150022; 2.武汉理工大学 土木与建筑学院, 武汉 430070; 3.哈尔滨工业大学 土木工程学院, 哈尔滨 150090)
0 引 言
针对土木工程结构开展抗震实验研究是获取结构抗震性能的主要手段。当前主要的抗震实验研究方法有拟静力实验[1]、拟动力实验[2]、模拟地震振动台实验[3]和实时混合实验[4-5]。其中实时混合实验方法兼具较高的实验精度与经济性,受到众多学者的关注。该方法将整体结构划分为物理子结构和数值子结构,分别进行物理加载与数值模拟,建立高速数据交互通道实现二者间的实时数据交互。但是由于实时混合实验要求实时,时滞便成了影响实验精度的主要问题,目前针对实时混合实验的研究工作集中在时滞与补偿上[6-7]。2016年,郭进等[8-9]提出了基于全局迭代的混合实验方法,该方法改变了传统实时混合实验方法的数据交互方式,将数据交互时间步长由积分步转变成了全时程,并通过离线迭代不断逼近真实结构响应,避开了时滞问题。当前针对迭代混合实验对不同结构适用性与物理子结构数值模型精度对迭代收敛性的影响,尚需要开展进一步研究。
笔者以安装有黏滞阻尼器的单层框架为研究对象,将框架内的黏滞阻尼器作为物理子结构,其余部分作为数值子结构,分别进行了不同结构阻尼比与物理子结构数值模型精度下的迭代混合实验数值模拟,比较了不同工况的迭代收敛速度和收敛精度,探究了结构阻尼比和初始物理子结构数值模型精度与收敛性对迭代混合实验收敛速度和收敛精度的影响规律。
1 实验方法及流程
迭代混合实验方法源于实时混合实验方法,实时混合实验方法运动方程为
MNaN,i+CNvN,i+KNdN,i+FE,i=Fi,
(1)
式中:MN、CN、KN——数值子结构的质量矩阵、阻尼矩阵、刚度矩阵;
aN、vN、dN——数值子结构的加速度向量、速度向量、位移向量;
FE——物理子结构反力向量;
F——结构的外荷载向量;
i——积分步数。
引入迭代思想,在方程(1)中增加迭代轮次这一变量。在迭代过程中,首先对整体结构进行全时程数值计算,得到物理子结构全时程加载命令,再对物理子结构进行全时程加载,加载结束后采集当前轮次的全时程试件反力,并将该反力带入运动方程,进行下一迭代轮次的运动方程求解,迭代混合实验方法运动方程为
式中,j——迭代轮次。
该方法的原理如图1所示。

图1 迭代混合实验方法流程Fig. 1 Direct of iterative hybrid test method
迭代混合实验方法的具体流程如下:
(1)模型建立。将整体结构划分为物理子结构和数值子结构,建立物理子结构数值模型。
(2)迭代启动。迭代首轮利用物理子结构数值模型,进行整体结构的纯数值计算,得到整体结构全时程力-位移响应。
(3)反力采集。将上一步得到的物理子结构位移响应在作动器上进行加载,得到真实的物理子结构全时程反力响应。
(4)多轮迭代。将上一步采集的物理子结构反力带入运动方程当中,代替物理子结构,进行下一轮整体结构全时程数值计算。
(5)收敛判断。将计算得到的物理子结构全时程位移与参考解进行比较,若收敛则实验成功结束,若不收敛则进行最大轮次判断。
(6)轮次判断。由于迭代不可能无限制进行下去,因此需要在实验前预先设定一个最大迭代轮次,进行迭代轮次判断。若当前轮次小于最大迭代轮次,则返回第(4)步,否则实验失败结束。
由图1可知,该方法的物理子结构与数值子结构相互独立,在迭代过程中一个完整时程仅进行一次数据交互,这样对于数值子结构部分而言,不再需要与物理子结构实时通信,逐步积分过程变成了纯数值计算,对于物理子结构而言,加载过程变成了给定加载制度的加载方式,这在避开时滞问题的同时,解决了逐步积分算法稳定性的问题,具有其独特的优势。
但是该方法由于其迭代的特点,在对于不同类型的结构会表现出不同的收敛特征,同时由于迭代首轮需要假定物理子结构数值模型,不同的模型精度对迭代收敛性的影响规律是需要研究的问题。
2 单层框架迭代混合实验数值模拟
2.1 工程概况
为了研究结构阻尼比与物理子结构数值模型精度对迭代收敛速度与收敛稳定性的影响,开展整体结构为安装有黏滞阻尼器的单层框架的迭代混合实验数值模拟,单层框架迭代混合实验原理如图2所示。由图2可知,将黏滞阻尼器作为物理子结构,剩余部分作为数值子结构。在迭代首轮,分别建立物理子结构数值模型和数值子结构有限元模型,进行全时程数值计算,得到单层框架全时程响应。在迭代次轮,利用上一迭代轮次加载得到的物理子结构全时程反力代替物理子结构本身,参与运动方程求解,计算出物理子结构全时程位移命令,再将命令传输给作动器进行加载,依次循环直至实验结束。本文中上述实验过程通过Matlab编程模拟,定义框架质量mN=3.6×105kg,框架刚度KN=1.24×105kg,框架阻尼比作为模拟研究的变量,分别取值为0.5%、1.0%、1.5%、2.0%、2.5%。
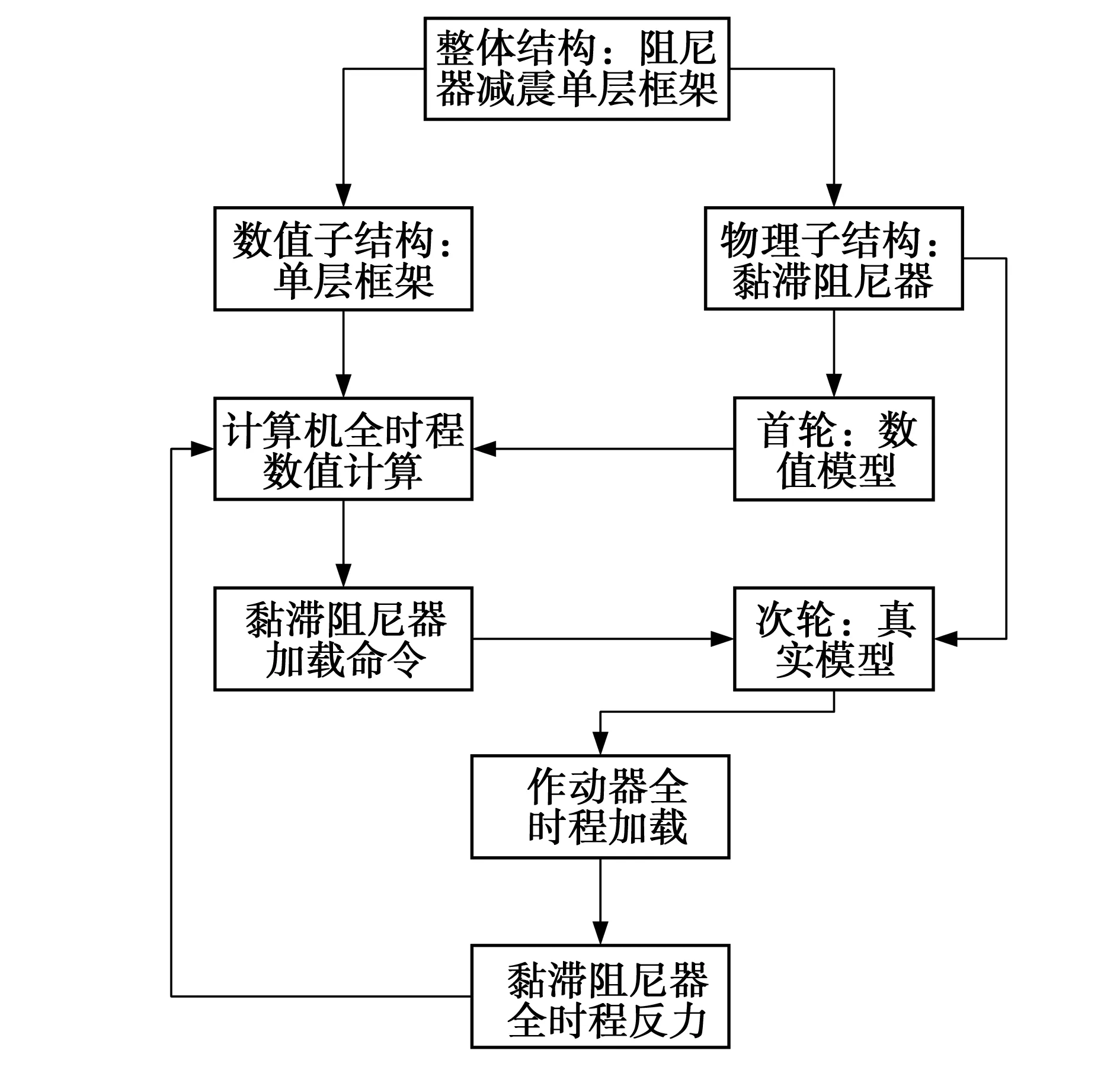
图2 单层框架迭代混合实验原理Fig. 2 Principle of iterative hybrid test of single layer frame
物理子结构为黏滞阻尼器,其力学模型为
FE=cEsgn(vE)|vE|α1,
(2)
vE——物理子结构速度向量;
α1——黏滞阻尼器速度指数。
在迭代混合实验首轮,需要假定物理子结构数值模型。为了研究不同模型精度对迭代收敛性的影响,分别假定模型精度为0、20%、40%、60%、80%,需要说明的是,模型精度为0即无阻尼器,仅仅针对数值子结构的框架开展迭代混合实验模拟。地震波选择EL centro波如图3所示,激励时长20 s,积分步长0.01 s,积分步数2 000步。
由于黏滞阻尼器恢复力计算要以当前步速度为输入,因此积分算法选用文献[10]中的方法,该方法为显式两步的数值积分方法,可以将位移、速度、加速度显式表达,且不需要用到结构的参数,具体积分格式如下:
aN,i=(Fi-CNvN,i-KNdN,i-FE,i)/mN,
dN,i+1=dN,i+vN,iΔt+(1/2+ψ)·aN,iΔt2-ψaN,i-1Δt2,
vN,i+1=vN,i+(1+φ)aN,iΔt-φaN,i-1Δt,
式中,φ、ψ——翟方法引入的参数。

图3 EL centro地震波Fig. 3 EL centro ground motion record
在逐步积分第一步,定义dN,1=vN,1=0、φ=ψ=0;在后续积分过程中,定义φ=ψ=0.5,此时其最大稳定步长与中心差分法相同。
2.2 工况设计
拟开展的模拟工况如表1所示。工况1~5为不同阻尼比下的迭代混合实验模拟,工况6~10为不同物理子结构数值模型精度的迭代混合实验模拟。
疼痛可以直接影响到病人的生活质量,疼痛发作时,机体会出现一系列地病理和生理反应,同时会让患者主观出现不悦的感受,在心理上给患者造成了巨大的困扰,而这些因素又恰恰决定着化疗、放疗及相关的一些治疗能否继续进行。[3]疼痛是一些晚期癌症病人常见的临床表现,尤其是持久、强烈、无法忍受的疼痛,这些会经常引起一系列症状,如食欲发聩、睡眠不佳、焦虑、烦躁、忧郁、甚至消极抗拒治疗等等,从而使得病情恶化。因而改善患者的疼痛状况,缓解情绪反应至关重要。我们需要加强对患者疼痛方面的教育,使晚期癌症患者度过舒服、平静的终末期。

表1 模拟工况
为量化迭代收敛速度,定义收敛步数指标如式(3)所示,其物理意义为当前迭代轮次与参考解在第i积分步前的位移差值小于限定值,即认为当前迭代轮次收敛步数为i。该指标能够直接体现当前迭代轮次的迭代收敛积分步数,能直观反应收敛速度。其中收敛步数限定位移s根据实际情况定义,通常认为当该值小于参考解位移幅值的2%,即为合理取值范围。
(3)
式中:ε——收敛步数;
d0——参考解位移, m;
s——收敛步数限定位移, m。
为量化迭代过程中的收敛精度,定义绝对误差如式(4)所示,即当前迭代轮次内每一积分步与参考解差值的最大值,该指标能够反映当前迭代轮次内计算的位移时程与参考时程局部误差大小,以体现迭代收敛精度。
(4)
式中,σ1——绝对误差, m。
2.3 实验结果分析
不同阻尼比下迭代收敛位移时程响应如图4所示。可见随着阻尼比的增大,位移响应的幅值逐渐降低,这表明阻尼比越大,结构消能减震的能力越强,位移响应越小。不同阻尼比时迭代收敛速度如图5所示。

图4 不同阻尼比下阻尼器的位移响应 Fig. 4 Damper displacement response of different damping ratio
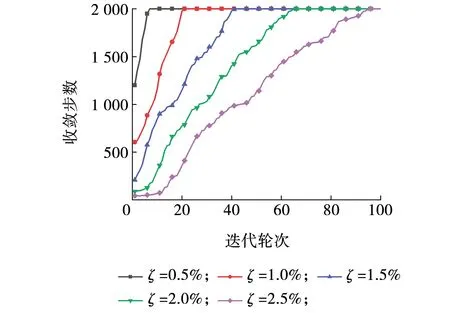
图5 不同阻尼比迭代收敛速度 Fig. 5 Iterative convergence rate of different damping ratio
由图5可知,结构阻尼比越小,相同迭代轮次下的收敛步数就越大。当阻尼比分别为0.5%、1.0%、1.5%、2.0%、2.5%时,完全收敛分别需要迭代7轮、21轮、42轮、65轮、96轮。通常开展迭代混合实验不超过20轮,由此可以认为,对于本次模拟选用的结构质量、刚度下,结构阻尼比ζ≤1.0%才能较好地利用迭代混合实验进行抗震分析。通常大型复杂结构的阻尼比往往较小,这将为开展迭代混合实验的收敛性提供保证,可见迭代混合实验对大型复杂结构较为适用。不同阻尼比的迭代误差如图6所示,当结构阻尼比为0.5%时,迭代100轮的绝对误差最大值为1.37 mm;当结构阻尼比为1.0%时,绝对误差最大值为51.22 mm;当结构阻尼比为1.5%时,绝对误差最大值为145.44 mm;当结构阻尼比为2.0%时,绝对误差最大值为267.62 mm;当结构阻尼比为2.5%时,最大绝对误差为397.78 mm,可见随着结构阻尼比的增加,物理子结构位移响应的绝对误差不断增加,迭代收敛精度下降。
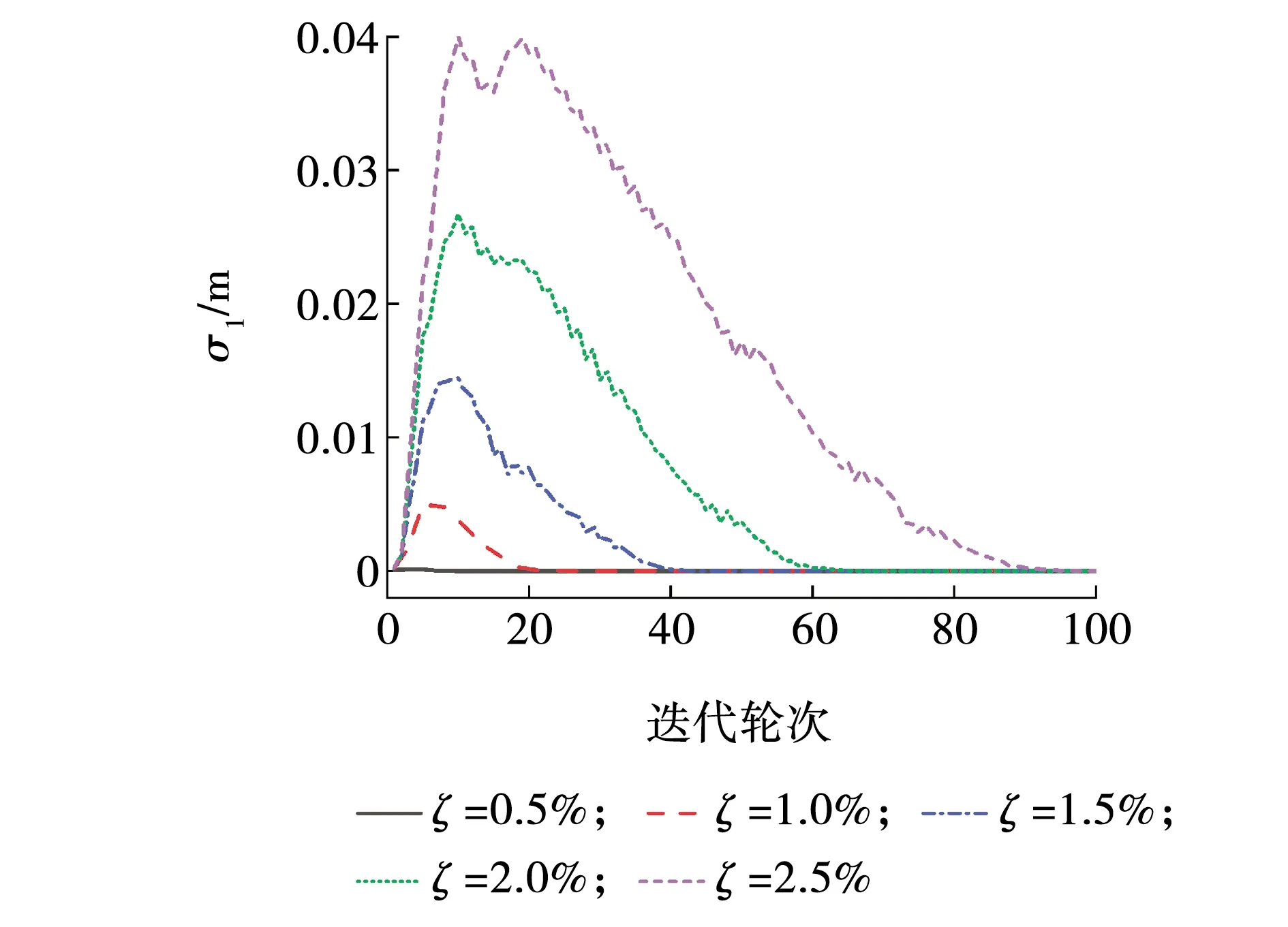
图6 不同阻尼比迭代误差Fig. 6 Iterative error of different damping ratio
不同黏滞阻尼器初始模型精度下迭代收敛速度如图7所示。由图7可知,物理子结构数值模型精度分别为0、20%、40%、60%、80%时,完全收敛分别需要迭代24轮、23轮、23轮、22轮、22轮,可见随着物理子结构数值模型精度的提高,迭代收敛速度无明显变化,模型精度从0提到至80%,完全收敛的轮次减少两轮。由此可以认为,物理子结构初始数值模型精度对迭代收敛速度影响不明显,即迭代混合实验对物理子结构数值模型精度鲁棒性较强。
不同阻尼器模型精度的迭代误差如图8所示。
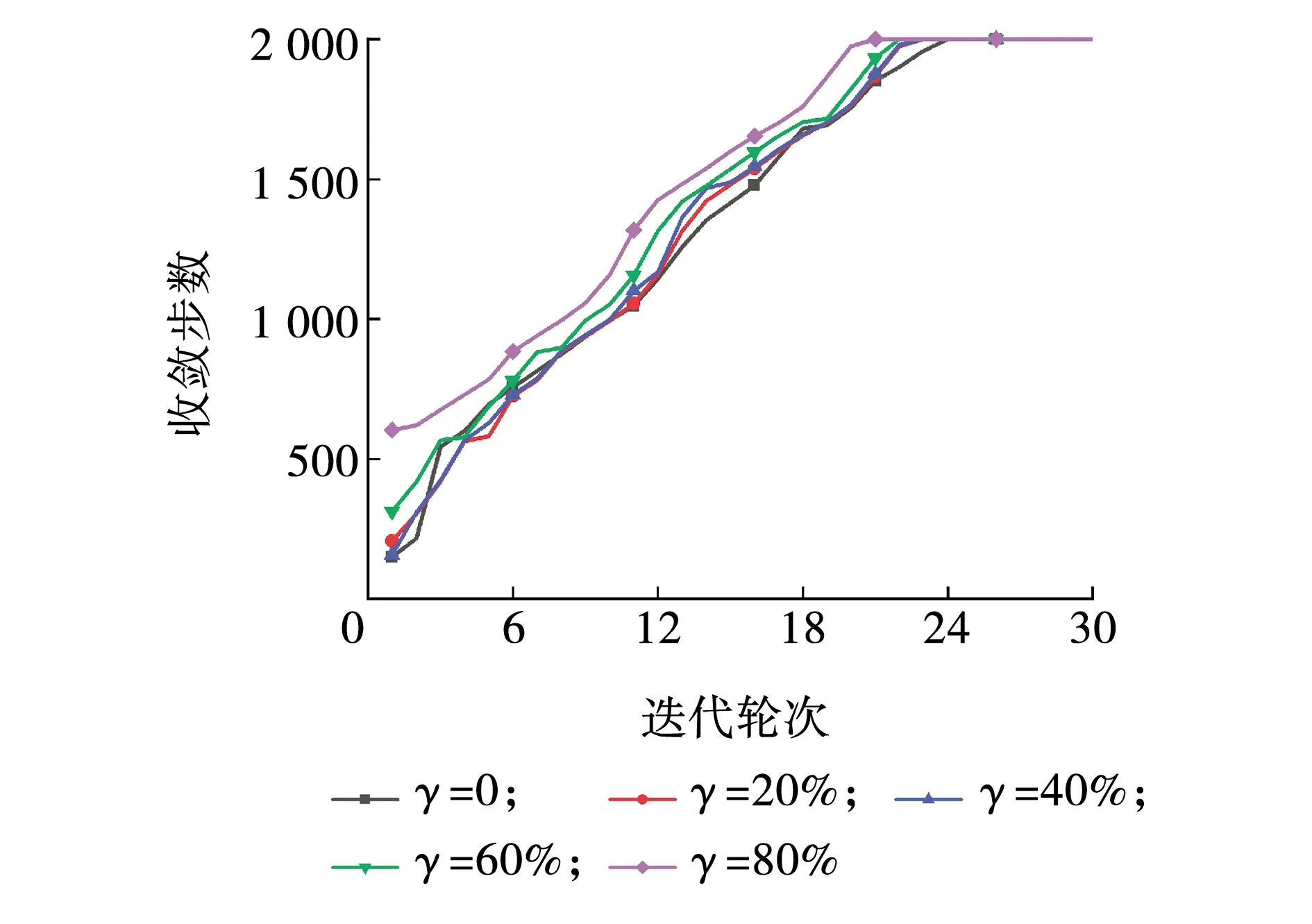
图7 不同阻尼器模型精度迭代收敛速度Fig. 7 Iterative convergence rate of different damper models accuracy

图8 不同阻尼器模型精度迭代误差Fig. 8 Iterative error of different damper models accuracy
由图8可知,当模型精度分别为0、20%、40%、60%、80%时,绝对误差最大值分别为127.94、102.98、92.75、76.45、51.22 mm,表明随着模型精度的提高,迭代误差降低,迭代收敛精度提高。
3 结 论
(1)结构阻尼比越小,迭代收敛速度与收敛精度越高。针对本文模拟对象,当阻尼比分别为0.5%、1.0%、1.5%、2.0%、2.5%时,完全收敛分别需要迭代7轮、21轮、42轮、65轮、96轮,可见当阻尼比小于等于1.0%时,迭代混合实验收敛速度较快,满足迭代混合实验收敛速度要求。
(2)物理子结构数值模型精度越高,迭代收敛精度越高,迭代收敛速度无明显变化。当模型精度分别为0、20%、40%、60%、80%时,完全收敛分别需要迭代24轮、23轮、23轮、22轮、22轮,可见迭代混合实验对物理子结构数值模型精度鲁棒性较强。

