一种利用剩余容量的电动汽车充电站无功补偿控制策略

刘 思，沈 广，胡金迪，叶承晋

（1.国网浙江省电力有限公司营销服务中心，杭州 310007；2.浙江电力交易中心有限公司，杭州 310007；3.浙江大学 电气工程学院，杭州 310027）

0 引言

随着电动汽车保有量逐年增长以及“新基建”的推动，电动汽车充电站的规模将进一步扩大。如何进一步利用充电站的可调节容量成为当下研究的热点。多数研究从规划层面着手，使充电站分布尽可能吸引车辆充电[1-2]。文献[3]采用两层求解策略，以总投资成本、运行成本和失负荷成本最小为目标，实现满足传统负荷与电动汽车充电负荷需求的配电网规划；文献[4]结合路径选择模型与交通满意度评价模型，建立了总成本最小、网损最小、交通满意度最高的充电站与分布式电容的选址定容模型；文献[5]根据交通流量、出行特性以及站网成本，对充电站的选址定容进行优化规划。但针对已有充电站，需要从控制层面考虑提升容量利用率。

另一方面，对于现有充电站可以通过有序充电的方式提升充电效益[6-8]。文献[9-10]分别考虑了负荷的影响因素与时空特性分布，建立充电负荷预测模型，为引导有序充电提供预测基础；文献[11]考虑用户充电推移时间，引导有序充电，从而降低负荷峰谷差；文献[12]提出了一种基于新电价机制激励用户调整充电时间的有序充电策略，提高充电设施利用率，减小充电排队对公路交通的影响；文献[13]提出了V2G 模式下的电动汽车有序充放电控制模型，从而减少充电费用、减小负荷方差。但目前关于利用率提升的研究多集中于有功功率控制，而具备整流逆变功能的充电桩同时具有无功响应的能力，针对聚合充电站剩余无功响应潜力的电压控制策略还缺乏深入研究。

本文从利用充电站无功补偿潜力的角度实现充电桩剩余容量的有效利用，提高充电站的利用率。首先建立充电站内调控充电桩有功功率、无功功率的控制模型，并采用MPC（模型预测控制）进行求解。然后在配电网内各充电站之间共享各自的功率、电压信息，实现台区内的协调控制；最后，通过算例验证本文提出的无功补偿控制策略能有效利用充电站的剩余容量，提升配电网充电站节点电压质量。

1 充电站有功、无功交互原理

1.1 充电桩无功补偿原理

充电站内的充电设施为非车载充电机，其交直流转换装置为三相六脉桥式结构[14]。该结构下，对功率期间的关断可调整交直流变换器输出电压的波形，从而控制功率传输。因此，充电桩可实现有功功率、无功功率的双向互动，发挥与柔性无功补偿装置同样的优化配电网运行的作用。充电桩功率传输范围由充电桩容量约束，其有功、无功运行约束如式（1）所示[15]：

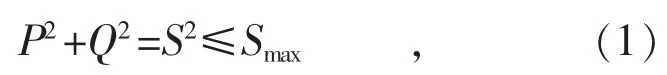
式中：P 为充电桩的有功功率，定义向电动汽车充电为正方向；Q 为充电桩的无功功率，定义充电桩吸收感性无功为正方向；S 为视在功率；Smax为充电桩额定容量。

1.2 站内充电桩聚合响应原理

通过控制充电站内多个充电桩实现聚合响应，汇聚单个充电桩的无功响应容量，从而有效优化电网电压质量。充电站内多桩聚合示意图如图1 所示。

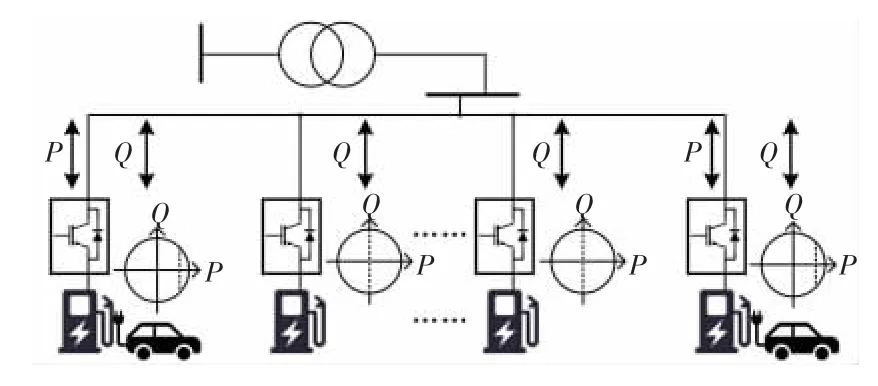
图1 充电站内多个充电桩聚合示意图

图1 中坐标系内虚线为对应充电桩的无功补偿潜力，若无电池充电，可接入电容来实现无功传输。由于单个充电桩的容量较小，需要聚集多个充电桩的无功来实现大容量、长持续时间的资源集群，从而提升充电站的无功补偿效果。

2 充电站调控框架

2.1 充电站调控总体框架

如图2 所示，以充电站j 为例，充电站j 接收来自配电网台区内其余充电站的功率以及电压数据，同时测量自身所在节点的电压。然后以下属充电桩的有功、无功功率为控制变量，进行MPC 计算，确定其有功、无功输出。充电桩接收到设定值后调整自身运行状态，调控其有功、无功输出，最终在满足电动汽车充电需求的同时，实现最优无功响应。

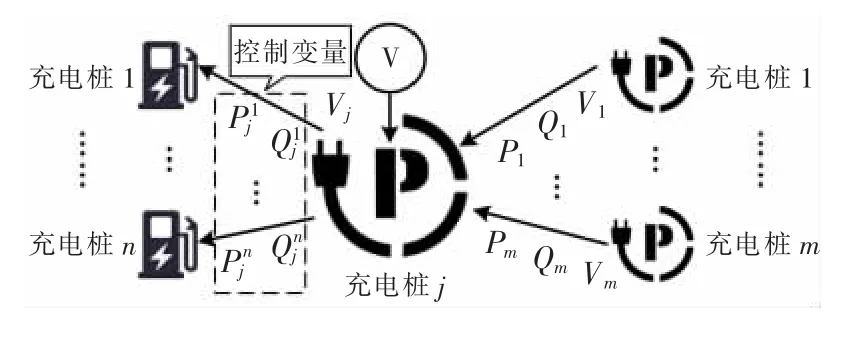
图2 充电站控制框架示意图

2.2 充电站MPC 模型建立

MPC 计算流程如下：首先设定固定时间周期并确定控制周期数与预测周期数，每当新的周期开始，求解预测模型，计算设定预测周期内的最优功率解，并传递至下属充电桩；然后，当下一周期开始时，重复模型求解以及设定值传递的流程，从而修正较长预测周期带来的偏差，形成滚动优化的机制[16]。

2.2.1 无功补偿目标函数

各充电站根据接收到的数据，调整站内充电桩的功率，达到配电网台区内充电站连接节点整体电压偏差最小的目的。其目标函数如式（2）所示：

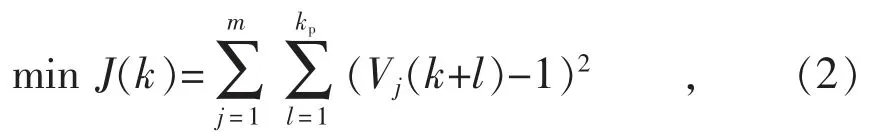
式中：k 为目前所在的周期；m 为配电网台区内充电站数量；kp为设定的预测周期数；Vj（k+l）为充电站j 在第k+l 周期的电压预测值。

2.2.2 充电站电压状态方程

通过灵敏度矩阵来预测充电站电压，灵敏度矩阵由对应配电网的雅各比矩阵求逆得到。模型中状态变量为各充电站电压，控制变量为站内各充电桩的有功、无功。以充电站j 为例，其状态方程如式（3）—（8）所示：

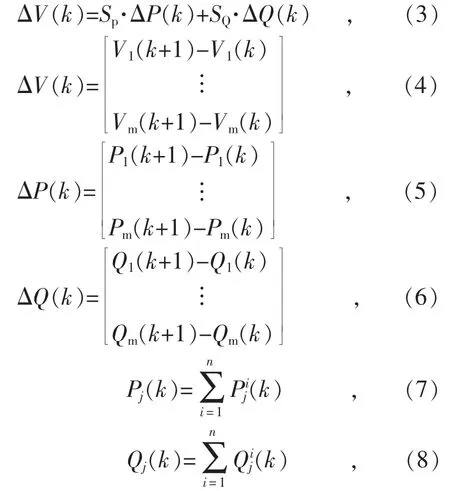
式中：ΔV（k）为各充电站节点电压在第k 周期内的增量向量；ΔP（k），ΔQ（k）分别为各充电站有功功率、无功功率在第k 周期内的增量向量；Pj（k），Qj（k）分别为充电站j 内各充电桩有功、无功之和，其余充电站的有功、无功为通信获得的数据；分别为充电站j 内充电桩的有功功率、无功功率，为MPC 模型中的控制变量；SP，SQ分别为节点电压关于有功、无功增量的灵敏度矩阵。

2.2.3 无功补偿约束条件

充电站的有功、无功设定值受到所属各充电桩的充电状况以及容量的约束，具体约束条件如式（9）、式（10）所示：

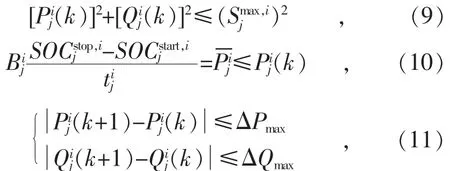
式（9）为充电桩容量约束，确保充电桩在额定范围内运行。式（10）为充电功率约束，保证充电桩能满足设定的充电需求。若充电站存在未接入车辆充电的充电桩，则令其对应的有功功率0。式（11）为充电功率变化率约束，防止功率突变影响用户充电体验与损坏充电桩。

3 充电站数据共享机制

充电站数据共享机制如图3 所示。充电站首先接收来自其他充电站的功率、电压预测数据，并在控制周期初始时刻测量自身所在节点的电压，随后进行MPC 计算。计算结束后，充电站需要将有功、无功设定值传递至对应的下属充电桩，同时将该站的功率、电压预测数据共享至其他充电站。

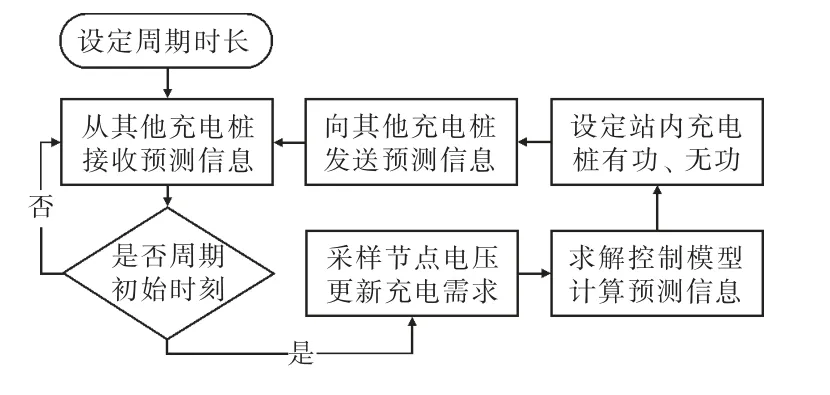
图3 数据共享流程

充电站与下属充电桩发送的数据内容为当前周期各充电桩需要输出的有功、无功值，站内各充电桩接收到信息后调整各自交直流变换器的运行状态，使其功率输出达到设定值。某充电站与其他充电站共享的数据为其自身所处节点在未来设定预测周期内的功率以及电压的预测数据，以此作为输入参数进行MPC 求解，实现各充电站之间的协调控制。

4 算例分析

4.1 仿真参数设置

本文采用IEEE 33 节点算例对所提无功补偿控制策略进行仿真[17]，其电网拓扑如图4 所示。在图中充电圆圈标注的节点接入充电站，电网基准功率设为100 MVA，基准电压为12.66 kV，设置节点1 为平衡节点。

图4 IEEE 33 节点电网拓扑

充电站的参数设置如下：每个充电站各有30个充电桩，每个充电桩的额定容量为10 kVA，假定每个充电桩接入电动汽车的充电需求概率分布如表1 所示。若按概率分布生成的充电需求大于设定的功率最大值，则增大充电时间直到等于功率最大值。

表1 电动汽车充电需求概率分布

4.2 无功补偿效果

根据充电站参数生成充电负荷，仅充电的场景下电压分布如图5 中虚线所示。此时电压质量较差，多数节点电压超过5%的范围。在此场景下，各充电站开始调整所属充电桩的有功、无功输出，对电网进行无功补偿，相关控制参数如下：每次控制的时间周期设定为1 s，控制预测的周期数均为5；每周期内有功功率、无功功率变化的最大值分别为1 kW，1 kvar。充电桩无功补偿后，各个充电站的有功、无功功率分别如图6、图7 所示。在充电桩无功补偿支撑下的电网电压分布如图5 中实线所示，可见，在无功补偿后电压质量得到明显改善。

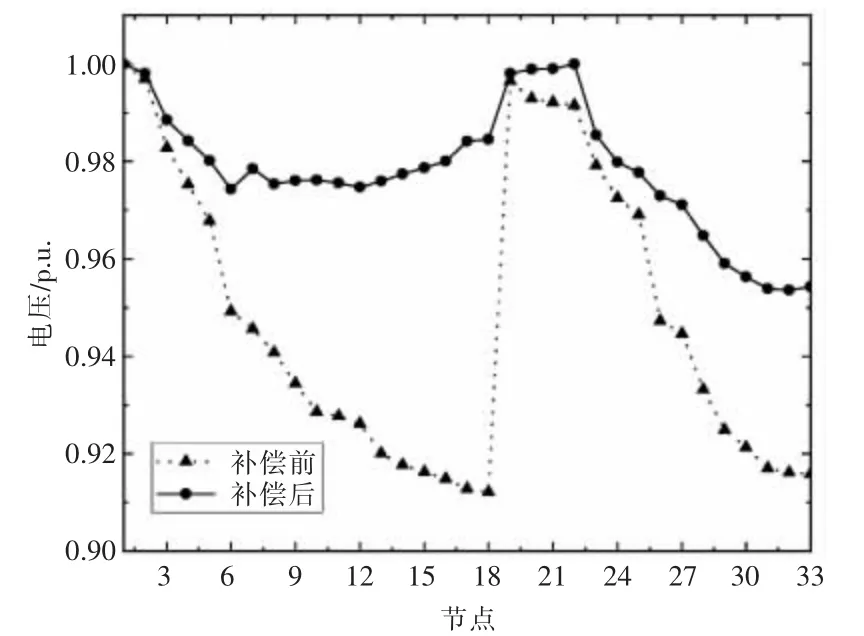
图5 无功补偿前后电压分布对比

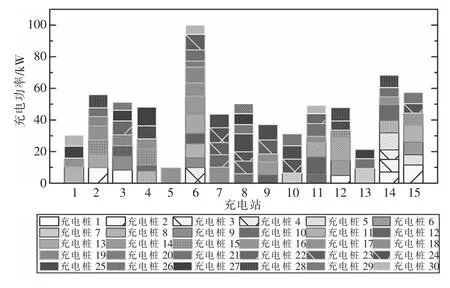
图6 充电站内各充电桩有功功率

图7 充电站内各充电桩无功功率

为量化比较无功补偿前后电压质量的改善效果，定义电压质量指标如下：

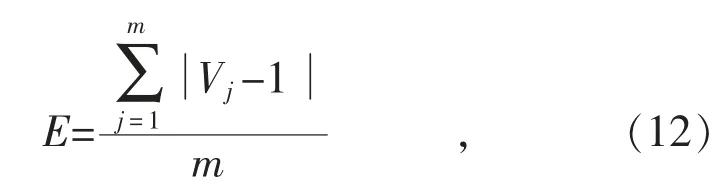
式中：E 为电压质量指标；Vj为充电桩j 的电压；m 为充电桩数量。

无功补偿前后电压质量指标分别为0.052 和0.216，调压后电压质量提升了58.5%，仿真结果表明本文提出的无功补偿控制策略能有效改善电压分布，提升电压质量。

4.3 容量利用情况

在配电网中各充电站的无功补偿输出稳定后，各充电站的有功、无功输出情况与容量利用情况如表2 所示。可以看出，若不参与无功补偿，多数充电站的有功功率不到100 kW，充电站的容量利用率较低。参与无功补偿使充电站的限制容量得到利用，在为配电网提供无功补偿、提升电压质量的同时，提高了充电站的容量利用率，从而有效缓解了充电设施利用率低的问题。

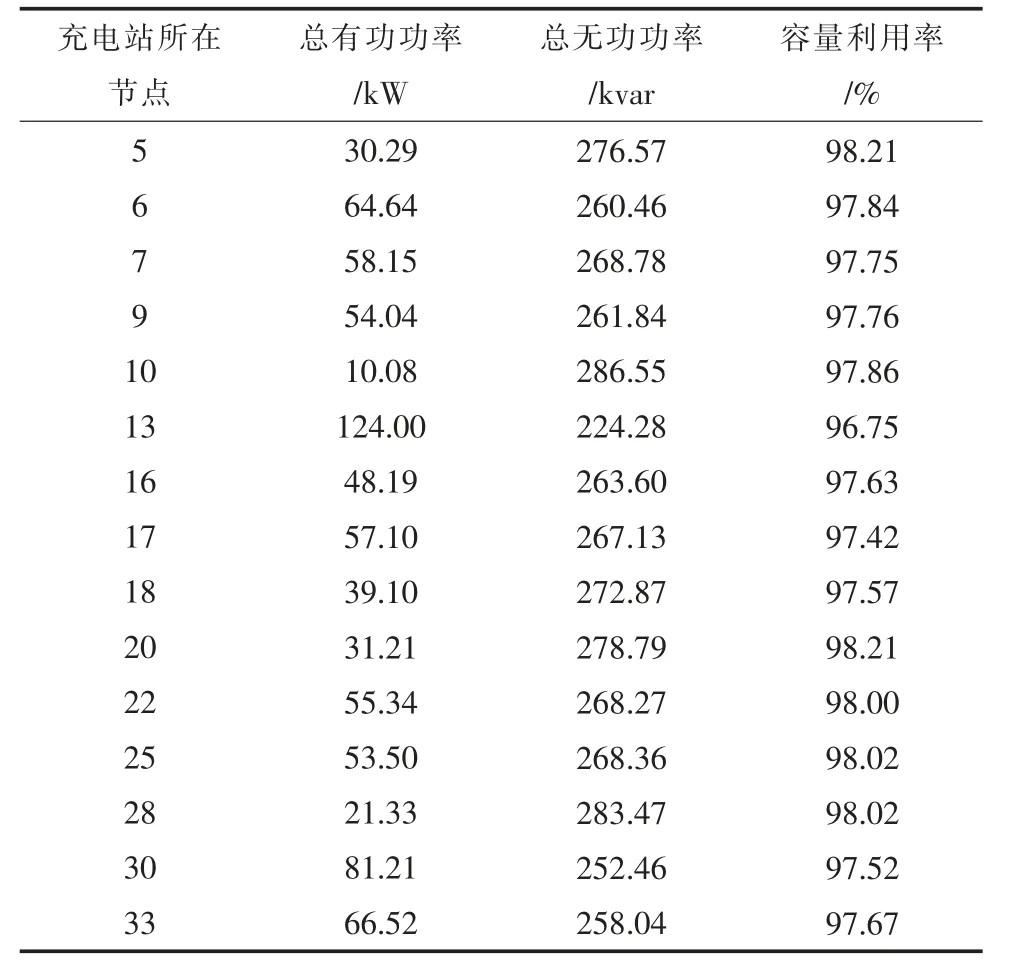
表2 各充电站有功、无功、容量利用情况

4.4 电压预测分析

为验证本文所提充电站电压预测模型的准确性，本节以配电网中末端节点18 为例分析节点电压的预测准确度。位于节点18 的充电站关于所处节点的电压预测值如图6 所示，电压预测值与电压实际值基本一致，且在15 s 左右电压值逐渐稳定。可见，本文提出的无功补偿模型预测控制策略能准确预测节点电压的变化，实现精准补偿。此外，电压波形呈阶梯上升趋势，这是因为防止功率突变的约束条件导致补偿功率逐次递增，避免功率剧烈变化，从而保障用户的充电体验与充电桩的工作寿命。

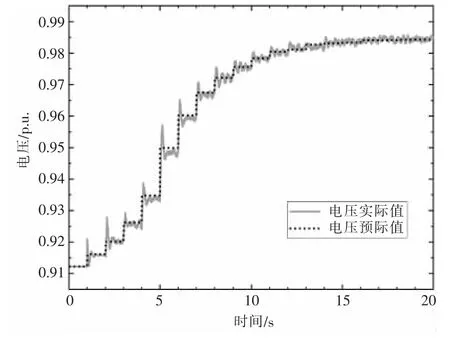
图8 节点18 电压预测曲线

5 结语

本文利用三相六脉桥拓扑下充电桩具有V2G四象限功率传输性能的特点，建立了配电网内充电站及其下属充电桩的控制策略，并共享各充电站的功率以及电压预测数据。本文提出的控制策略有效利用了充电站内各充电桩的剩余容量，同时可改善配电网的电压质量，并通过各充电站之间的协调配合实现了充电站所在节点电压质量整体最优的无功补偿。

接下来将进一步研究充电设施利用率提升问题，优化控制策略，并结合物联网思想进一步完善共享机制。