CT26型断路器操动机构动力学仿真及拐臂疲劳寿命分析

王增彬，张 拓，姚聪伟，孙 帅，王立军

（1.广东电网有限责任公司电力科学研究，广州 510080；2.广东省电力装备可靠性企业重点实验室，广州 510080；3.西安交通大学电力设备电气绝缘国家重点实验室，西安 710049）

0 引言

高压开关是电网中的关键设备之一，起着控制和保护电路的双重作用，是电力系统安全可靠运行的重要保障。在电力系统发生的事故中，由开关设备引起的故障占很大比例[1]，严重影响电力系统安全可靠运行。第三届CIGRE 断路器可靠性报告指出，断路器故障原因占比最高的是操作机构机械故障[2-4]，因此对断路器机械特性进行研究十分必要。断路器在长期运行过程中，部分受力大的部件可能会出现疲劳损伤，GB 1984—2014[5]对此作出相关规定，因此需要对断路器机构的关键部件进行疲劳寿命分析。

随着数值仿真技术广泛应用于现代工业生产过程中，制造物理样机之前会建立虚拟样机进行仿真模拟，可以提前了解其性能，提出指导性意见[6-9]。国内外已有诸多学者对断路器的电弧性质进行了研究[10-11]，对断路器操动机构建立仿真模型，并计算其机械特性[12-15]。高压断路器操动机构属于机械装置，在其长期运行过程中还应考虑疲劳损伤。国内对于疲劳损伤问题的研究起步较晚，但仍取得许多研究成果[16-18]。文献[19]利用多体动力学软件Adams 建立真空断路器操动机构的虚拟样机，并对断路器的分合闸过程进行了仿真；文献[20]利用机械系统多体动力学分析软件Motion 与液压系统仿真软件AMEsim 建立联合仿真模型，对420 kV 高压液压操动式断路器机构进行了仿真分析；文献[21]基于ANSYS Workbench以及nCode DesignLife 软件对断路器缓冲器缸体进行有限元疲劳寿命分析，为缓冲器及弹簧操动机构其他零部件的疲劳分析提供了一种新的分析路径和方法。

本文基于Adams 和AMEsim 软件建立仿真模型，对252 kV 高压断路器CT26-252 型弹簧操动机构分合闸过程的运动情况进行仿真计算，同时对机构运动过程中受力较大的零件进行疲劳寿命计算。

1 断路器结构与计算原理

1.1 断路器机构结构简介

252 kV 高压断路器CT26-252 型操动机构为弹簧储能式机构，其整体模型如图1 所示。

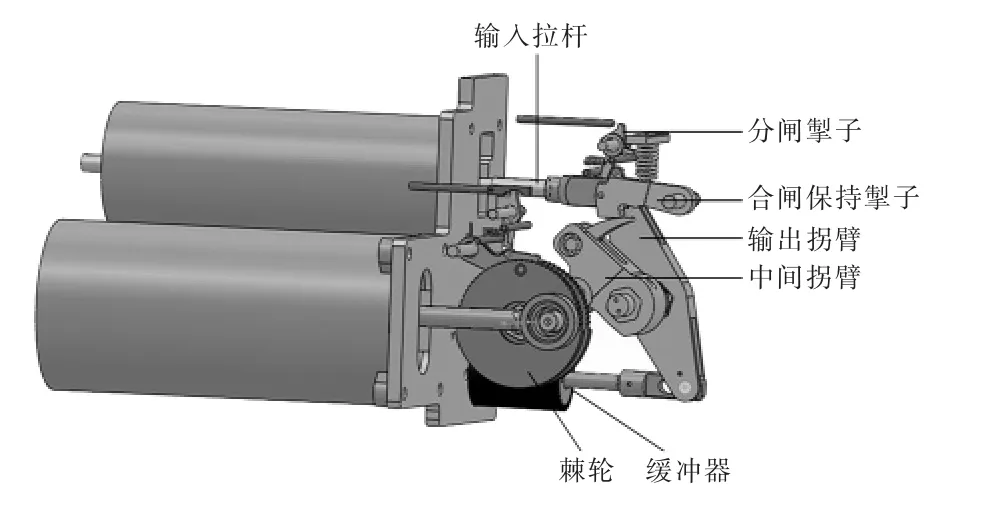
图1 断路器操动机构三维模型

断路器处于分闸状态，且合闸弹簧已储能时，机构状态如图1 所示。合闸过程中，合闸线圈动作，释放分闸保持掣子，合闸弹簧带动储能轴旋转，凸轮撞击拐臂滚子，主轴旋转，带动断路器动触头运动，同时为分闸弹簧储能，直到合闸保持挚子扣接，完成合闸过程；分闸阶段，分闸线圈动作，释放合闸保持挚子，在分闸弹簧的作用下主轴旋转，完成分闸过程。

由于分、合闸触头动作速度较高，会对机构及灭弧室零部件造成冲击，因此通常采用添加缓冲装置的方式来吸收运动部位的分合闸剩余动能，防止冲击力过大造成断路器零部件损伤。CT26-252 型操动机构采用油缓冲器进行缓冲。油缓冲器是一个液压系统，剖视图如图2 所示。

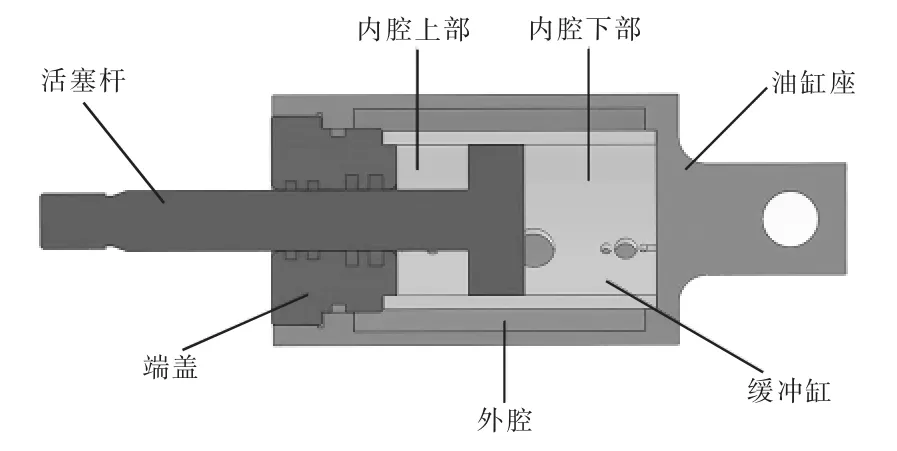
图2 油缓冲器剖视图

1.2 断路器操动机构仿真原理

采用动力学仿真设计是复杂机械系统优化设计的主要手段之一，能够真实地模拟机构零部件运动过程，对多种参数方案进行量化分析，减少样机制造的试错次数，缩短产品研制周期与成本。由于油缓冲器属于简单液压系统，Admas 为机械系统仿真分析软件，不能对油缓冲器部分进行仿真，因此本文联合采用Adams 与液压仿真软件AMEsim，对断路器分合闸过程的机构运动情况进行仿真。仿真流程如图3 所示。

图3 操动机构仿真流程

在SolidWorks 中建立断路器操动机构的模型，并将该模型导入Adams 中进行相应设置，同时在AMEsim 中建立油缓冲器模型，通过仿真软件的数据接口完成联合仿真。

为了分析机构关键部件的应力应变情况，研究部件受力形变对机构运动的影响，需要建立刚柔性混合动力学模型，对断路器机构运动进行更加精确的模拟。基于Adams 的刚柔混合动力学模型仿真分析流程如图4 所示。

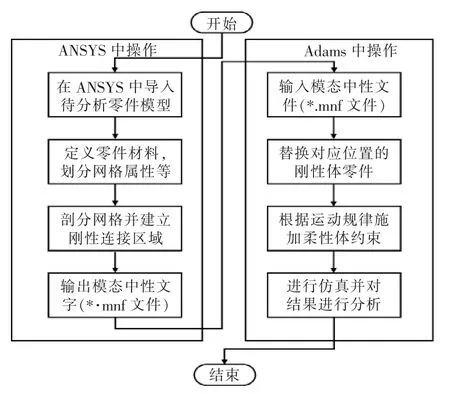
图4 基于Adams 刚柔混合动力学模型仿真流程

通过刚柔混合动力学模型仿真不仅可以得到柔性体部件在机构运动过程中的应力应变情况，还可以得到在该过程中柔性体部件的载荷谱，为疲劳寿命分析提供基础数据。

1.3 疲劳寿命仿真原理

若构件在循环恒幅应力S 的作用下，承受N次循环载荷产生疲劳损坏，则其在承受n 次循环时的损伤量化值D 如式（1）所示：

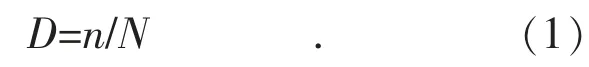
假设构件在应力水平Si作用下，承受ni次循环时的损坏为Di=ni/Ni。若构件承受的一次载荷历程包括k 个应力水平Si（i=1，2，3，…，k）的作用，每一个应力水平Si包括ni次循环，则可以定义一次载荷历程下的总损伤如式（2）所示：

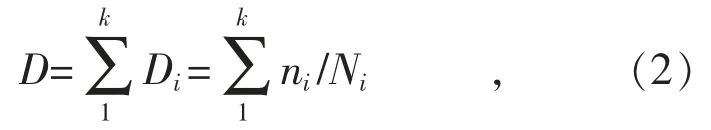
式中：ni为Si作用下的循环次数，由载荷谱确定；Ni为Si作用下的疲劳寿命，由S-N 曲线确定。

构件产生疲劳破坏的判断依据为D=1。

依据上述方法，使用ANSYS workbench 对构件进行受力分析，获取构件应力分布，从Adams中导出构件的载荷谱。将应力分布与载荷谱导入nCode 进行求解分析，得到疲劳寿命计算结果。

2 仿真过程及结果分析

2.1 断路器操动机构仿真

2.1.1 多刚体动力学模型仿真结果

采用Adams 与AMEsim 联合仿真的方法，将断路器操动机构的各个零件简化为刚体模型，将缓冲器部分按照液压系统计算。其中，分闸弹簧弹性系数为156 N/mm，预紧力为10 750 N；2 个合闸弹簧并联，弹性系数分别为120 N/mm 和85 N/mm，预紧力分别为28 560 N 和19 290 N。断路器机构的分合闸示意图如图5 所示。

图5 断路器机构示意图

仿真时为了减少不必要的计算耗时，在合闸完成且停止弹跳后约40 ms 便让其开始分闸动作。计算得到输出拐臂在分合闸过程中的机械行程曲线如图6 所示。

图6 分合闸过程中拐臂输出位移

为验证仿真结果的准确性，利用机械特性测试仪实际测量同型号机构的分合闸行程曲线。断路器分闸过程中的实验结果与仿真结果对比如图7 所示，可以看出，分闸行程曲线的实验结果与仿真结果基本吻合，验证了仿真模型的准确性。

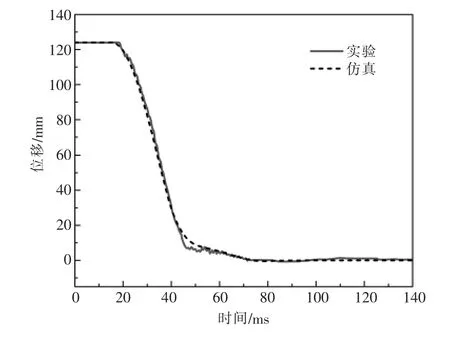
图7 拐臂行程实验结果与多刚体动力学模型仿真结果对比

2.1.2 刚柔混合动力学模型仿真结果

在断路器分合闸过程中，操动机构中的输出拐臂将承受很大的力，可能在动作过程中产生形变，从而影响机构运动。因此考虑将机构中的输出拐臂替换为柔性体进行计算，用柔性体代替输出拐臂后的模型如图8 所示。将仿真得到的输出拐臂行程与实验值进行对比，结果如图9 所示。

图8 刚柔混合动力学模型示意图

由图9 可以看出，刚柔混合动力学模型仿真结果与实验结果基本一致，且分闸过程中的速度都在42 ms 处发生突变。原因是断路器操动机构在运动到约42 ms 时，油缓冲器中连接内腔下部与外腔的油孔全部关闭，油缓冲器对机构的反作用力瞬间增大，导致分闸速度下降。

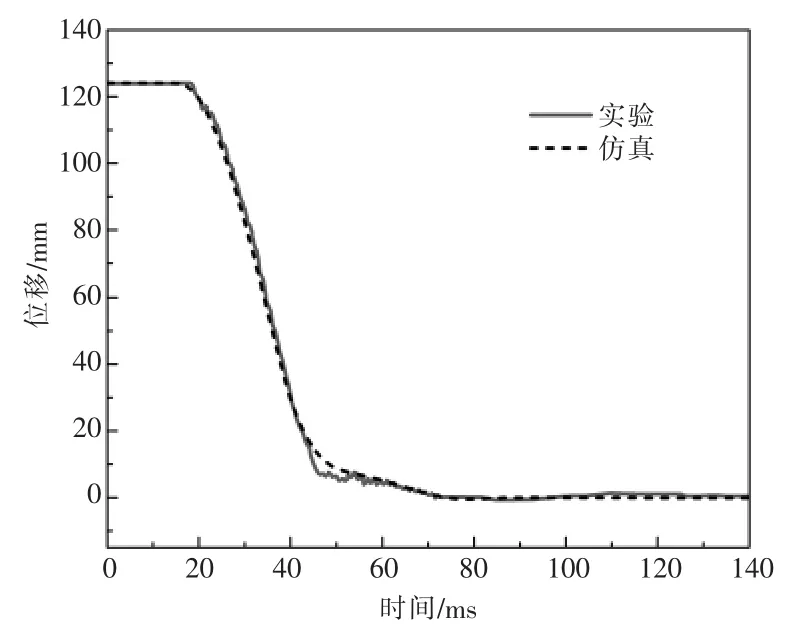
图9 拐臂行程实验结果与刚柔混合模式仿真结果对比

多刚体模型和刚柔混合动力学模型的输出拐臂位移对比如图10 所示。可以看出，多刚体动力学模型与刚柔混合动力学模型的仿真结果基本一致，将拐臂替换为柔性体后对机构整体运动模拟影响小。

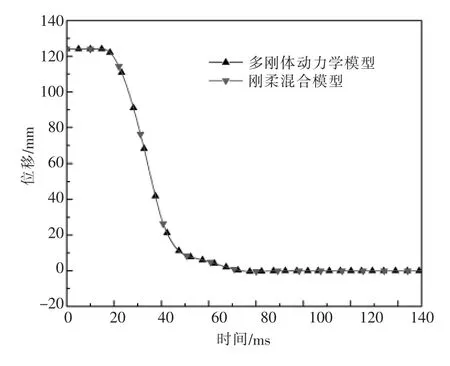
图10 2 种仿真模型的结果对比图

断路器运动过程中输出拐臂应变最大的10个点的应变情况如表1 所示，输出拐臂最大应变为0.002 25。可见，由于输出拐臂在断路器机构运动过程中应变量小，所以刚柔混合动力学模型与多刚体动力学模型的仿真结果基本一致。

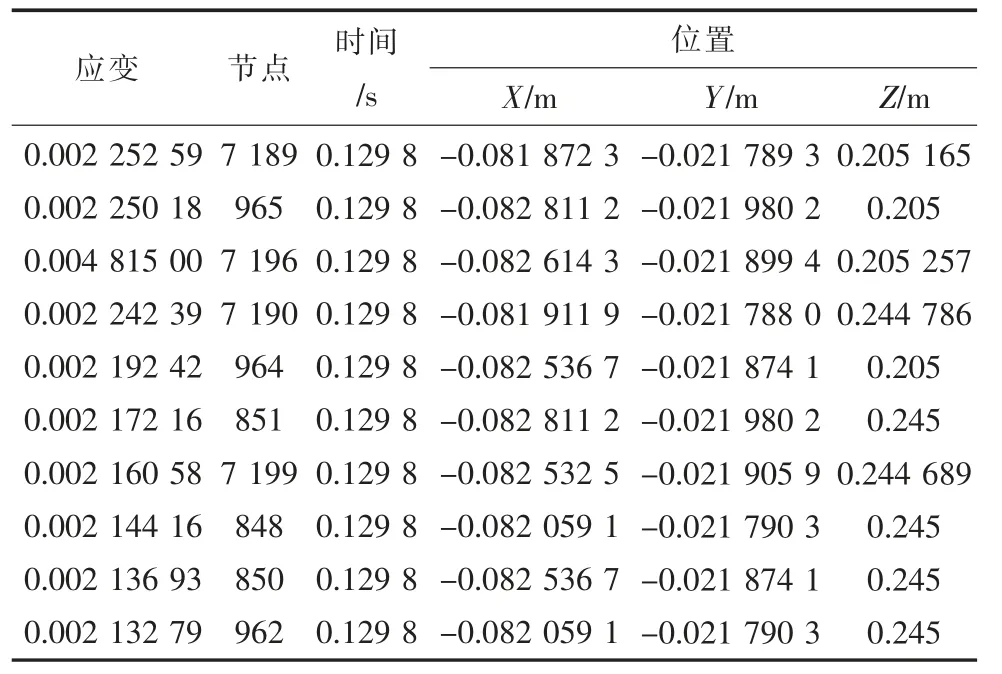
表1 断路器分合闸过程中拐臂应变最大节点信息

通过刚柔混合动力学模型可获得断路器操动机构动作过程中的输出拐臂载荷谱。分合闸过程中，输出拐臂的载荷谱如图11 所示。由图可见，在分合闸过程中拐臂上下孔载荷存在差异：合闸过程中，拐臂上孔存在较大载荷，而下孔载荷较小；分闸过程中，拐臂上下孔载荷变化趋势相似，但下口承受载荷较大。这是因为拐臂下孔与油缓冲器相连，所以在合闸过程中载荷较小。

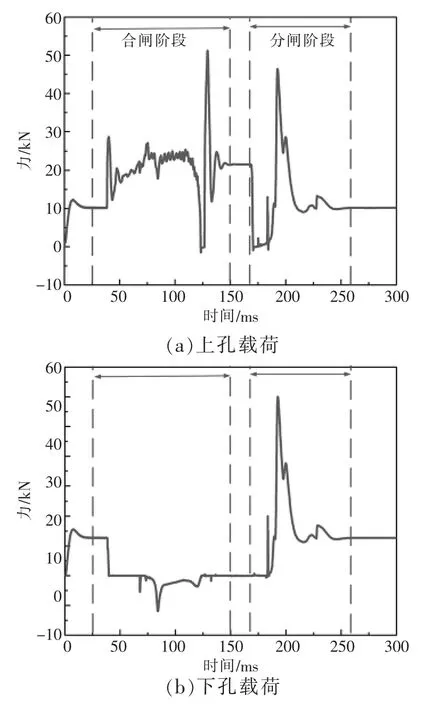
图11 拐臂的载荷谱

2.2 疲劳寿命计算

2.2.1 有限元分析结果

利用nCode 软件对拐臂进行疲劳分析时，需要读入有限元分析结果，所以首先需要利用ANSYS Workbench 对拐臂进行有限元分析。断路器分、合闸过程中，拐臂受力情况差别较大，可将其分解为两种工况，每种工况下的受力值由载荷谱决定。第一种工况下设置拐臂中孔为固定约束，上孔受力为51.2 kN；第二种工况下设置拐臂中孔为固定约束，下孔受力为59.99 kN。两种工况下拐臂受力设置如图12 所示。

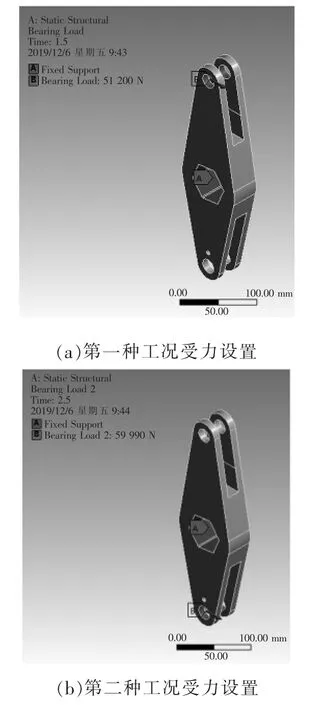
图12 拐臂受力设置情况

由图13 得知，两种工况下的最大应力应变分别在上孔和下孔附近，最大应力分别为563.47 MPa 和656.86 MPa，最大应变分别为0.002 8 和0.003 3。

图13 两种位置下应力和应变分析结果

2.2.2 疲劳寿命仿真结果

利用nCode 软件对拐臂进行疲劳寿命分析。拐臂材料为40Cr，材料的抗拉强度为750 MPa，将有限元分析结果以及载荷谱导入nCode 软件，得到拐臂疲劳寿命云图如图14 所示。可见，拐臂的上下孔处疲劳寿命最短，说明在该位置处更容易产生裂纹，最短寿命位于拐臂下孔，为60 430次，可满足国标中对断路器能够进行10 000 次操作的要求[5]。

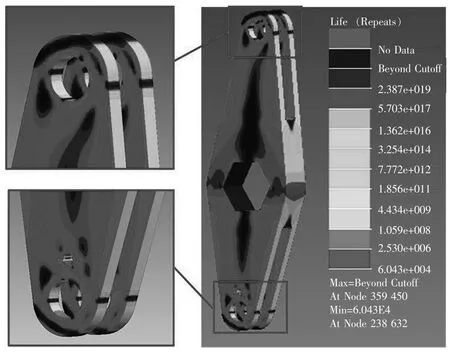
图14 拐臂疲劳寿命云图

3 结论

本文基于多体系统动力学理论和液压缓冲理论，采用Adams 软件和AMESim 软件联合仿真的方法，建立了带油缓冲器的高压断路器弹簧操动机构动力学仿真模型，对断路器分合闸过程中操动机构的动作情况进行仿真，并与实验结果进行对比；同时采用疲劳寿命分析软件对关键部件的疲劳寿命进行仿真，得到以下结论：

（1）利用Adams 与AMESim 建立联合仿真模型，对断路器分合闸过程进行仿真，得到的输出拐臂行程曲线与实验值基本一致，验证了联合仿真模型的正确性，为含缓冲器的断路器机构仿真提供了新的分析方法。

（2）对比多刚体动力学模型仿真结果与刚柔混合动力学模型仿真结果可知，由于拐臂在断路器操动机构运动过程中应变量较小，机构整体运动受拐臂应变的影响较小。

（3）在断路器机构合闸过程中，拐臂上通孔受力大于下通孔，且两者的载荷谱差异大；在分闸过程中，拐臂上通孔受力小于下通孔，两者的载荷谱变化规律相似。

（4）对拐臂进行疲劳寿命计算后发现，拐臂疲劳寿命可达到60 000 次以上，拐臂疲劳寿命最短位置处于拐臂下通孔位置。