工艺调度对乙炔加氢反应器优化运行策略的影响分析

谢府命，许锋，罗雄麟

（1中国石油大学（北京）自动化系，北京102249；2海南大学信息与通信工程学院，海南海口570228）

引 言

乙炔加氢反应器是乙烯工业中的重要装置[1-5]，它的主要作用是通过乙炔的加氢反应将高浓度乙烯流中的少量乙炔转化为乙烯，避免造成后续的乙烯聚合反应的催化剂中毒。由于反应需要钯金属催化剂有选择地使少量乙炔发生催化加氢反应，才能保证出口乙炔含量满足工艺需求，因此催化剂活性成为了关系到装置运行及经济效益的重要指标。反应器内催化剂则会受到温度及反应副产物影响，活性缓慢降低，当活性降低到一定程度，选择性无法满足工艺需求时，反应器停止运行，进行催化剂再生。

反应器中催化剂的反应活性和选择性可以通过反应器内温度和入口的加氢量进行调节，因此具有很大的操作优化空间。操作优化的首要前提就是建立精确的乙炔加氢反应器模型。乙炔加氢反应器模型分为拟均相模型[6-8]和非均相模型[9-10]，拟均相模型较为简单，易于实现，非均相模型则精确度较高，但计算复杂，实现难度大。反应器内催化剂的失活模型是乙炔加氢反应器模型的重要组成部分，当前的研究中，基于催化剂失活动力学，不同程度上考虑了反应器的温度，低聚物的累积效应对催化剂活性的影响，建立了精确的催化剂失活模型[11]。并且，针对催化剂活性在长周期运行内的不可测变化，设计了高效的活性在线估计器，实现长周期运行的活性准确估计[12]。

当前，在乙炔加氢反应器建模中充分考虑了慢时变特性的影响，根据催化剂活性的变化规律建立了相应的数学模型，并通过经济效益、能耗等生产指标构建乙炔加氢反应器的优化模型，求解并得到乙炔加氢反应器的全周期的操作优化[11-14]。通过动态分析可以发现过程的操控性能对设计裕量的要求[15-18]，为保证操作和控制的要求，必须留出一定的裕量，保证系统的正常运行。控制性能要求越高，所需设计裕量越大，设计裕量大小与控制系统设计有关。设计裕量可分为工艺裕量与控制裕量[19]。在实际过程中，尤其是乙炔加氢反应器一个再生周期可能持续几个月，期间会受到各种因素的影响，其中可预测的影响如催化剂活性，在设计阶段，按这类因素的最大影响计算出一部分设计裕量，称之为工艺裕量；不可预测的影响因素有很多，这类随机性影响一般可通过控制系统的操作弥补，在设计阶段，按控制器的需要留出部分设计裕量，称之为控制裕量。工艺裕量在未达到设计时所预想的“最坏”情况时，设计裕量并未完全释放，除去消耗的控制裕量和释放的工艺裕量，存在部分剩余裕量，将会为过程操作优化提供一定空间。

为了能充分利用这部分剩余裕量，必须考虑集成控制与操作优化的一体化方法。目前，这类方法较为著名的是“back-off”方法，能够估计不确定状况对系统造成的影响，适用于稳态优化模型[20-23]和较为复杂的非线性动态优化模型[24-28]。类似的方法还能进一步集成设计、控制和调度[29]，也能获得很好的控制优化效果。Xie等[30]以乙炔加氢反应器作为研究对象，构建了集成优化和控制的慢时变系统优化框架，并提出了一种能充分利用剩余裕量的动态优化方法（裕量缓释操作优化方法）。裕量缓释操作优化简单而言，就是在已有的全周期动态优化的基础上，通过裕量估计的方法，实现全周期的剩余裕量估计，并最大限度利用这部分剩余裕量，来提升系统的优化控制性能。

在全周期操作优化过程中，若将这部分剩余裕量提前释放，必然导致运行周期的缩短。而工艺人员在设定运行周期时，要求到运行周期结束时化工装置性能恰好能达到过程约束边界，即慢时变参数达到“最坏”情况，设计裕量恰好释放完毕。这部分剩余裕量的最优释放特性，必然与慢时变参数的变化规律相关，释放机制也只可能与运行周期的设定有关。

考虑在实际工业生产中，常出现由于生产调度的原因临时变更操作优化方案的情况。若系统在按照操作优化方案运行一定时间后，需要在剩余运行周期内临时改变操作方案，在这类情形下剩余裕量的最优释放特性及全周期优化结果将与之前文献讨论的原始全周期操作优化产生一定的差异。本文基于二维非均相乙炔加氢反应器模型，研究了这类在运行周期中临时改变操作优化方案的全周期动态优化问题。改变操作优化方案的方式包括：变更运行周期、追求经济效益最大化和变更优化目标、追求运行周期最大化。通过对这两种改变操作优化方案的分析，探讨改变操作方案对裕量释放特性、运行周期和经济效益的影响。

1 问题的提出

现有的文献对于乙炔加氢反应器全周期操作优化的研究，都是基于一定的运行周期内操作优化策略不变这一前提。但是，在实际工业生产过程中，乙炔加氢反应器不一定能在整个运行周期中保持同一优化的操作策略，有时因调度需求需要在运行过程中临时更改反应器运行周期或优化目标等，这会使得裕量缓释操作优化中最优的裕量释放特性发生变化，从而导致最终优化结果的变化。讨论这类临时改变优化策略的意义在于解决长周期运行的系统中因临时调整策略对剩余运行周期和经济效益等的预估问题，以及全周期内多个不同优化策略的分段裕量缓释操作优化问题。

一般地，对于慢时变系统的裕量缓释操作优化问题，最优的剩余裕量释放特性只与设定的运行周期相关，设定较短的运行周期，则剩余裕量释放较快，能获得较大的平均每日经济效益；反之，则释放较慢，能获得较大的全周期整体经济效益；在达到最大运行周期时，系统性能恰好能够达到约束边界。临时改变操作策略的裕量缓释操作优化显然也应该遵循这一规律。

举例如下，如图1所示，由于工业调度的具体需求，在运行过程的某一时间点（图1中为D点）需要临时改变运行周期，裕量的最优释放特性也应该发生相应的改变，如图1中的虚线部分，即曲线a和曲线c分别为临时减小和增大再生周期所获得的经济效益曲线和可用剩余裕量的变化曲线。曲线b则是按原定优化操作方案运行而不做临时改变所获得的经济效益曲线和可用剩余裕量的变化曲线。运行周期变得更短，则将剩余裕量较快释放完毕（即图中曲线a的可用剩余裕量更快地消耗殆尽）；反之，运行周期变得更长，剩余裕量则较为缓慢释放（即图中曲线c的可用剩余裕量更缓慢地降低），以保证装置的工艺性能。这一类临时更改运行周期的实际问题给全周期动态优化问题增添了新的挑战，实际的最优裕量释放规律是否符合图1中所推断的裕量释放规律，几种裕量释放策略在不考虑工业调度的硬性要求的情况下，哪种能获得更高的总体经济效益。如果在运行周期的更改点（即图1中D点）采用不同的优化策略，即以最大再生周期为优化目标，优化结果如何，所能获得的最大运行周期是否与优化策略更改点有关。

对于这一系列的问题将会建立乙炔加氢全周期的裕量缓释操作优化模型，同时将考虑两种改变操作方案的方式，包括变更运行周期、追求经济效益最大化和变更优化目标、追求运行周期最大化。通过对这两种改变操作方案的分析，对问题进行逐个解答。

图1 改变设定的运行周期问题表述Fig.1 Problem illustrated of the optimal margin consumption characteristic

2 工艺调度对优化策略的影响分析

2.1 全周期优化框架

乙炔加氢反应器模型是本文研究的基础，本文沿用了之前的反应器动态模型，即考虑低聚物累积影响的催化剂失活模型的二维非均相乙炔加氢反应器模型[11]。该模型研究了催化剂失活机理，并结合乙炔加氢反应器的二维非均相模型[10]，使得模型能够更加准确地反映乙炔加氢反应器长周期运行时，系统受催化剂失活影响的动态特性，能够充分满足乙炔加氢反应器全周期优化问题的模型精度需求。

本文考虑裕量缓释操作优化在运行周期中某一时间点发生优化策略改变的特殊情形，首先要构建乙炔加氢裕量缓释操作优化模型作为研究的实现框架。裕量缓释操作优化[30]是一种能通过估计全周期的剩余裕量，在整个运行周期内将这部分裕量缓慢释放，从而能获得更多的优化和控制的操作空间，达到提升优化和控制性能的目的。在之前的工作中，已经在乙炔加氢反应器中实现了裕量缓释操作优化方法，其全周期获得的整体经济效益要远大于传统的保留所有设计裕量进行优化的全周期动态优化[30]。并且，还通过建立一般裕量缓释的动态优化模型，通过推导证明其能够适用于一般的慢时变系统。因此，本文的优化策略变更均在文献[30]的工作基础上进行。

另外，由于慢时变系统中存在的时间尺度不同的问题（即慢时变参数变化过于缓慢，而控制系统响应较快，无法在同一时间尺度下进行控制和优化），之前的工作中还建立了慢时变系统的全周期控制优化框架[30]，即构建快-慢时变系统并分别进行控制优化。本文的研究需要对全周期优化策略进行临时的更改，但是实际上也可以视为一个初值不同的裕量缓释操作优化问题，因此相应的控制优化框架与之前的裕量缓释操作优化类似，图2为临时改变优化策略后的控制优化框架图，Γc为临时改变优化策略的时间点，Γf′为临时改变后的反应器运行周期（Γf是改变前的运行周期）。系统的剩余裕量也需要根据Γc的活性θc和系统的状态变量xc进行重新估计。图中的具体的裕量估计模型和优化模型（模型1～7）将会在2.2、2.3节中详细叙述。

基于该控制优化框架，临时改变运行周期的动态优化必须要重新估计在改变运行周期后这一段时域内的剩余裕量，才能实现裕量缓释操作优化。因此，首先要建立工艺裕量、控制裕量和最优设计量的估计模型。

2.2 变更运行周期

在裕量缓释操作优化框架中，工艺裕量、控制裕量和剩余裕量的估计事实上可以通过求解优化模型实现，因此首先构造目标函数，动态优化的目标为一定再生周期内的最大整体经济效益，用反应物与产物，即乙炔、乙烯和氢气的经济效益来量化。Ea、Eb和Ec分别为第Γ日乙炔、乙烯和氢气的经济效益函数，具体为

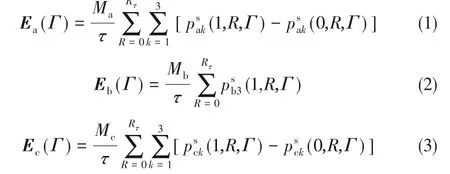
式中，p为反应器中的气体分压；下角标a、b、c分别代表乙炔、乙烯和氢气；下角标k为反应器床层的序号，k=1,2,3；上角标s代表非均相模型的催化剂相；R为反应器径向长度；Rτ为反应器器壁部分的离散区段。由式(1)～式(3)可以得到临时改变运行周期后这一段时域内的整体经济效益表达式为

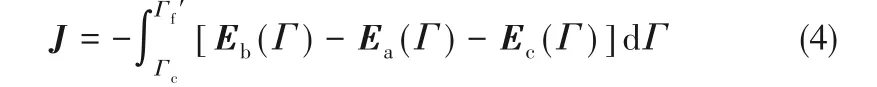
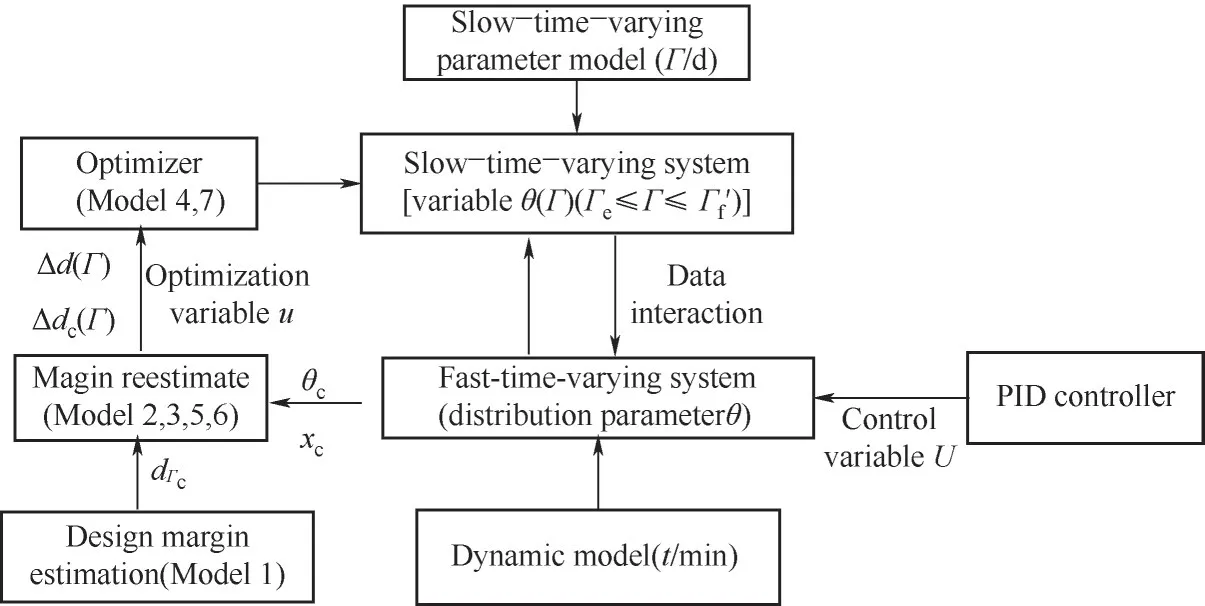
图2 临时改变优化策略后的优化框架Fig.2 Optimization frame after temporary change of optimization strategy

接下来，为了估计这段时域上的剩余裕量，首先应该求解整个运行周期的最优设计变量d0，最优设计变量实际上在改变运行周期之前的裕量缓释操作优化中就应该通过估计得出，即Model 1，再通过求解优化模型，估计相应的工艺裕量和控制裕量。

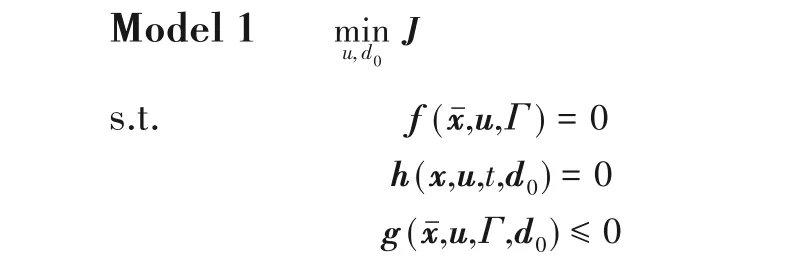
式中，f(·)、h(·)和g(·)分别为慢时变系统中的失活模型、快时变系统中的反应器动态模型和优化的不等式约束。这里用dΓc表示在Γc处系统的最优设计裕量与工艺裕量之和。

通过求解这一段时域内的优化模型，就能获得系统运行到第Γ天时相应的工艺裕量估计Δd(Γ)，其中Γ∈[Γc,Γf′]。

为了便于表示控制裕量的估计，用hs表示快时变系统中不含控制系统的稳态方程；用xˉ表示慢时变系统中的状态变量。接下来，考虑快时变系统中的控制作用，将控制器纳入优化模型中，得到控制裕量Δdc(Γ)。

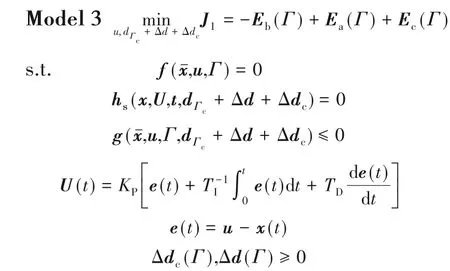
构造一个描述临时改变运行周期后，一段时域内操作点与约束边界之间距离的函数，即裕量消耗函数。基于Model 1的目标函数J，引入裕量消耗函数，得到考虑裕量消耗的动态优化模型——Model 4。

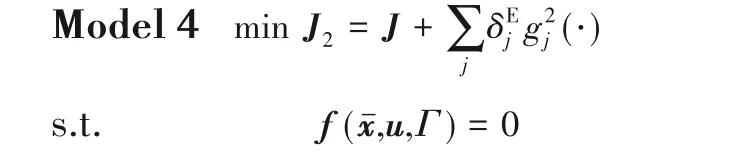
基于裕量缓释操作优化模型，以180 d作为乙炔加氢反应器的计划再生周期，求解得到固定运行周期180 d的最优工艺裕量消耗轨迹，如图3中的虚线所示。由于生产线调度等需求，有时需要临时改变再生周期，这里以点Γc=120 d作为临时改变点，原先的裕量缓释操作优化（即再生周期为180 d）的总裕量应保持不变。考虑固定剩余天数，将Γf′=150、160、170、190 d作为改变后的最大再生周期，实现这一段时域内的裕量缓释操作优化，其最优工艺裕量消耗轨迹如图3所示（总裕量一定，能反映相应的最优裕量释放轨迹），150、160、170 d的最优裕量释放速率较快，而190 d的最优裕量释放较为缓慢，改变运行周期的裕量缓释操作优化均能够在最大运行周期内恰好达到系统所允许的最大工艺裕量（占总裕量的70%左右），实现最优的经济效益。

图3 临时改变运行周期优化的最优裕量消耗Fig.3 Optimal process margin consumption for temporary change of operation cycle

由于反应器的再生周期是临时改变，系统的总裕量一定，因此Γf′＜180 d时，即小于运行前设定的运行周期时，剩余的裕量应该保持较快释放，以实现短期内更高的经济效益，Γf′＞180 d时，即大于运行前设定的运行周期时，剩余的裕量应保持更缓慢的速率进行释放，以保证在较长的运行周期内系统能够正常运行而不超出工艺约束。这一特性也完全符合前文对临时改变运行周期裕量缓释操作优化的最优裕量释放轨迹猜想。

接下来，考虑复杂化工过程的动态优化方法，采用CVP（控制向量参数化方法）[31-37]，即将连续的慢时变全周期优化变量转化为若干个参数变量进行求解，通过该方法给出求解Model 4所得到的全周期的经济效益曲线（包含不改变运行周期前的曲线）如图4。由于这部分裕量要在较短的周期内快速释放，150、160 d为最大运行周期时经济效益曲线还能保持一个较大的增长，直至出口乙炔含量超出过程约束，反应停止；170 d为最大运行周期时经济效益曲线和不改变运行周期的动态优化轨迹较为接近；相对应，为了实现更长的运行周期，190 d为最大运行周期时经济效益曲线下降较快。如表1所示，最大运行周期为Γf′=150、160、170、190 d的全周期总经济效益和年化经济效益，从全周期总经济效益来看，不改变运行周期（即最大运行周期为180 d）所获得的经济效益要高于临时改变运行周期的总经济效益，并且，临时改变的运行周期与原定周期差距越小，总经济效益的损失也越小。但是，从年化的经济效益（除去催化再生费用）来看，不改变运行周期的裕量缓释操作优化所获得的年化经济效益要低于临时改变的最大运行周期为Γf′=150、160、170 d的年化经济效益，并且大致以Γf′=160 d为年化经济效益的最优策略。

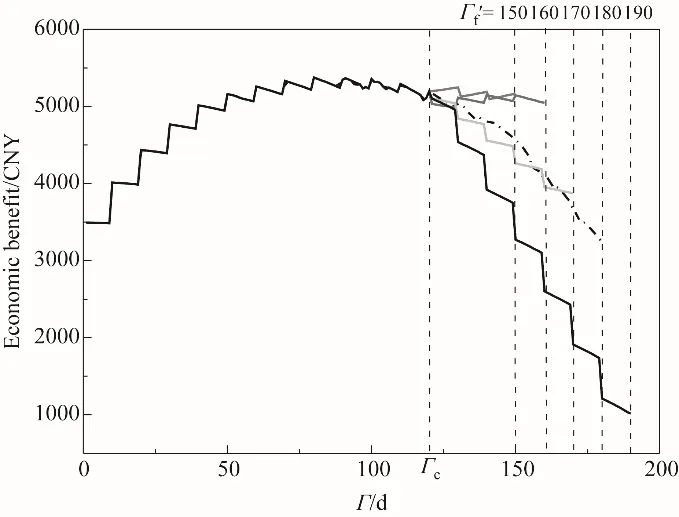
图4 临时改变运行周期优化的最优经济效益曲线Fig.4 Optimal economic benefit curve for temporary change of operation cycle

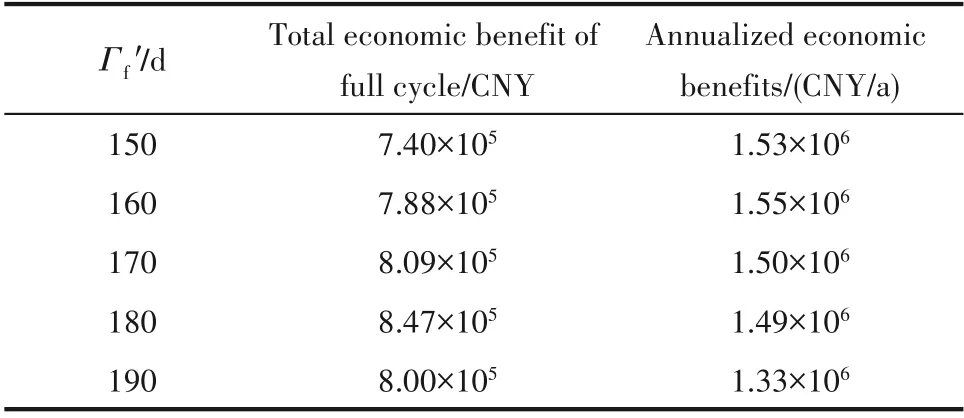
表1 临时改变运行周期的优化结果Table 1 Optimization result for temporary change of optimization strategy

实际上，根据动态优化的最优性原理，原定的裕量缓释操作优化必定是要优于临时改变运行周期的裕量缓释操作优化结果，这实际上在优化结果中也有体现。但是，年化经济效益相当于是以平均每日经济效益为衡算标准，这就造成了临时改变周期的优化，其裕量快速释放，所获得的年化经济效益可能要高于原定的裕量缓释优化。

2.3 变更优化目标

在乙炔加氢反应器按固定运行周期的裕量缓释操作优化运行一定时间后，常需要考虑系统能够维持运行的最大剩余天数的问题，这实际上相当于一个目标函数为最大再生周期的裕量缓释操作优化问题。并且，由于长时间运行过程中反应器内催化剂的失活效应，再生周期不可能无限延长。

接下来，考虑在Γc处改变优化策略的情形，具体为将原先的目标函数为经济效益，改为目标函数为最大再生周期的动态优化问题。这里仍将Γf′作为改变优化策略后反应器的最大运行周期，临时改变优化策略动态优化的目标函数为

以式(5)为目标函数，就可以构造目标函数为最大运行周期的动态优化模型。但是，由于目标函数是一个全周期变量，也是在进行裕量估计之前必须获得的关键量，因此无法按照前文估计目标函数为经济效益裕量的方法进行估计。这里采用一种折中的方法，即将最小活性下降量作为裕量估计模型的目标函数，裕量缓释操作优化模型仍然采用运行周期作为目标函数。

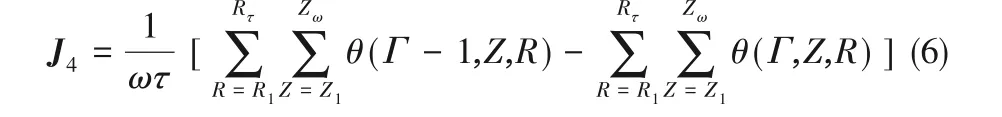
裕量估计的目标函数如式(6)所示，整个反应器作为分布参数系统，Z、R分别表示反应器轴向和径向变量，分别有

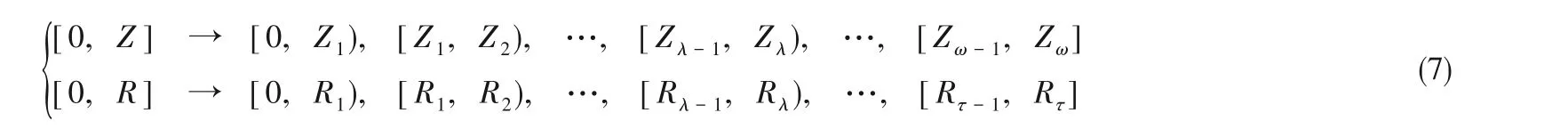
因此，可以通过优化模型Model 5和Model 6，来重新估计临时改变优化策略后，系统所需的最优工艺裕量和控制裕量，方法与前文类似。

接下来，可以构造目标函数为最大运行周期的裕量缓释操作优化模型为

接下来，考虑固定运行周期为180 d，目标函数为经济效益的裕量缓释操作优化过程中，分别以点Γc=90、120、150 d作为临时优化策略变更点，在之后的优化策略中改为目标函数是运行周期的裕量缓释操作优化。求解Model 7，即可以得到临时改变优化策略所获得的经济效益。如图5所示，改变优化策略后，工作点有一个大幅度的改变，导致经济效益下降，均在170 d后处于经济效益的亏损状态，但是所获得的最大运行周期均能达到180 d以上，大于目标函数为经济效益裕量缓释操作优化的运行周期。优化策略变更点为Γc=90 d时，能利用的剩余裕量较为充足，因此优化所能达到的最大运行周期为212.01 d；优化策略变更点为Γc=120 d时，所维持的最大运行周期要略低，为205.32 d；优化策略变更点为Γc=150 d时，能利用的剩余裕量较少，因此可优化操作空间也较小，所维持的最大运行周期仅为201.15 d。图5中的虚线为目标函数是运行周期的全周期裕量缓释操作优化，也可以理解为Γc=0 d的情形，能维持的最大运行周期为218.36 d，要大于其他临时改变优化策略所能维持的最大运行周期。实际上，能维持的最大运行周期与能利用的剩余裕量的多少有关，总体来说，相对于目标函数为最大运行周期的裕量缓释操作优化，目标函数为经济效益的裕量缓释操作优化对剩余裕量的消耗要快一些，因此就呈现出优化策略变更点越小，所能获得最大运行周期越大这一规律。

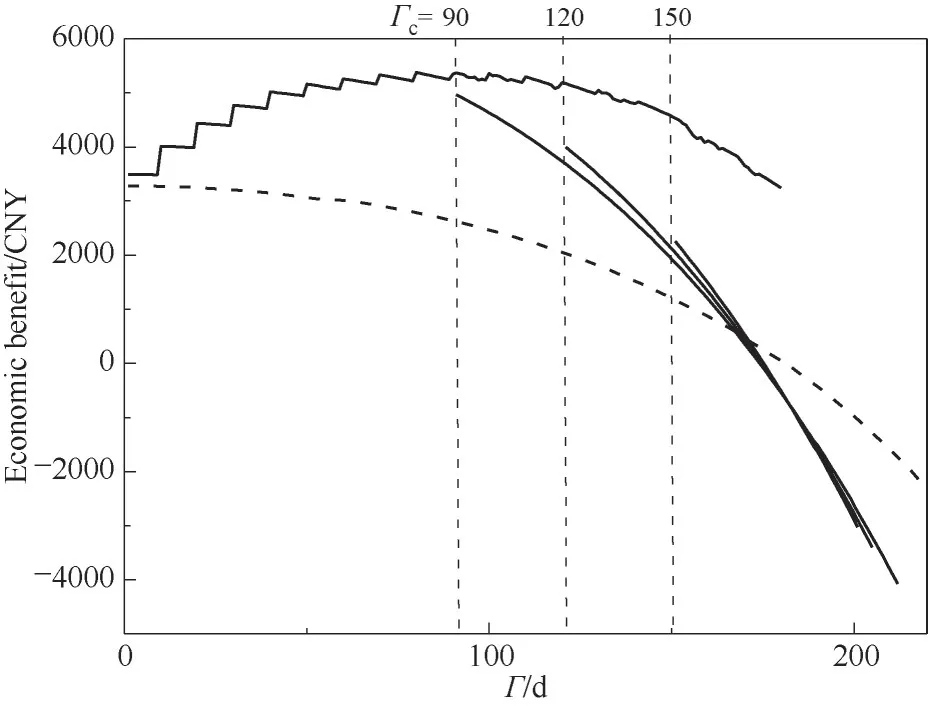
图5 临时改变优化策略优化的经济效益曲线Fig.5 Economic benefit curve for temporary change of optimization strategy

相反，优化策略变更点越靠前，所能获得的全周期总经济效益越低，优化策略变更点为Γc=90 d时，全周期总经济效益为5.93×105元；优化策略变更点为Γc=120 d时，全周期总经济效益为6.53×105元；优化策略变更点为Γc=150 d时，全周期总经济效益为7.22×105元；目标函数为运行周期的全周期裕量缓释操作优化，即Γc=0 d的情形，全周期总经济效益仅为3.77×105元。

3结 论

本文研究了裕量缓释操作优化在乙炔加氢反应器中，优化策略需要在运行期间临时发生变更的情况（包括变更运行周期和变更优化目标），通过构建优化控制框架，建立相应的优化模型，求解得到不同优化策略更改条件下裕量释放规律和经济效益曲线。

对于临时变更运行周期的裕量缓释操作优化而言，更改的运行周期越大，则最优裕量释放越缓慢；反之，则释放越快。在全周期总经济效益上的表现为不改变运行周期的原始操作优化方案大于临时变更运行周期的操作优化方案。但是，由于临时变更运行周期能使剩余裕量在短期内迅速释放，从而获得更高的年化经济效益。

对于临时变更优化目标（经济效益更改为最大运行周期）的裕量缓释操作优化而言，优化策略更改的时间点越接近运行起始点，则能够维持越长的反应器运行周期，但相应获得的全周期总经济效益就越少。

因此，从全周期的总体经济效益或运行周期的角度看，临时的工艺调度对乙炔加氢反应器的全周期优化运行总体上是不利的。