己二酸二甲酯加氢反应热力学分析及动力学研究

杨幸川，位根磊，徐丽，刘国际

（郑州大学化工学院，河南郑州450001）

引 言

1,6-己二醇（C6H14O2，HDOL）是一种重要的化工原料，可应用于生产聚氨酯胶黏剂、聚氨酯弹性体以及环保型涂料、黏合剂等多个领域[1-2]。HDOL具有两个端链羟基和较长的碳链，与乙二醇相比，以HDOL为原料制备的聚酯具有更为优异的柔韧性和抗腐蚀性[3]，因此，以HDOL为原料制造的新型高性能材料越来越受到用户青睐。近年来，全球HDOL市场规模不断增大，据预测，HDOL的市场规模将由2019年的9.02亿美元增长至2025年的14.01亿美元，年复合增长率为8%[4]。随着我国经济快速发展，国内对HDOL的需求量也逐年上升，HDOL对外依存度常年居高[1]，因此，需要加快国内HDOL工业化生产进程，开发具有自主知识产权的HDOL生产工艺，降低国内企业生产成本，提高抗风险能力。

采用己二酸或者己二酸酯，特别是己二酸二甲酯（DMA）加氢制备HDOL的生产工艺，因产物选择性高、反应流程简单、三废较少等特点而受到广泛关注[5-8]，是具有较好应用前景和较强竞争力的HDOL生产途径。反应热力学分析和动力学研究是研究化学反应过程的重要环节[9-10]。通过热力学分析可以知道反应发生的可能性、反应进行的程度以及外界条件对反应平衡的影响[11-13]。动力学研究是从动态角度研究反应条件对反应速率的影响，实现热力学的反应可能性[14-17]，对反应过程开发、反应器设计有着重要作用。而目前关于DMA加氢制备HDOL的热力学数据和动力学研究鲜有报道。基于此，本文采用基团贡献法[18-19]，对DMA加氢体系进行热力学数据估算，探讨了反应温度、压力等对Gibbs自由能变和反应平衡常数的影响；采用固定床反应器对DMA加氢本征动力学进行研究，获得了幂函数型动力学方程参数，以期为HDOL的生产优化和工业化设计提供参考。

1 反应体系热力学计算

1.1 各组分热力学数据估算

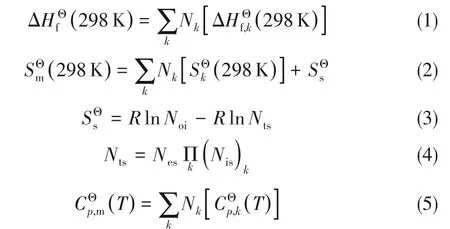
式中，Nts为总对称数，DMA和HDOL的总对称数分别为18和2；Noi为光学异构体数，对于本研究体系，各物质的光学异构体数均为1。计算所得摩尔标准生成焓、标准熵和比定压热容多项式回归结果列于表3。

DMA和HDOL的临界温度、临界压力和临界摩尔体积采用Joback法估算[24]，偏心因子采用Constantinou-Gani基团贡献法[20]进行估算。计算式如式（6）～式（11）所示：

表2 热力学基团贡献值：比定压热容（Benson法）Table 2 Thermodynamic data of group contribution of each component：heat capacity at constant pressure（Benson method）

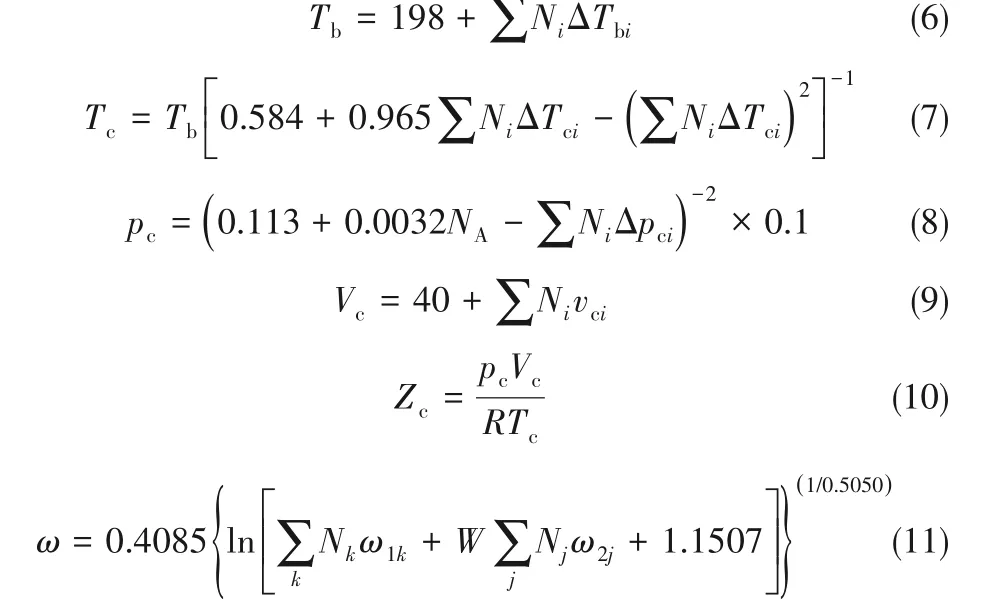
临界性质估算值和文献查得的甲醇与H2临界性质列于表4中。估算得到的DMA和HDOL的沸点与文献值[25]相对偏差分别为0.58%和0.86%，说明估算得到的结果是可靠的。

采用适用于高温高压条件下的Soave-Redlish-Kwang（RKS）状态方程计算混合物中各物质的逸度系数[26]，计算式如下：

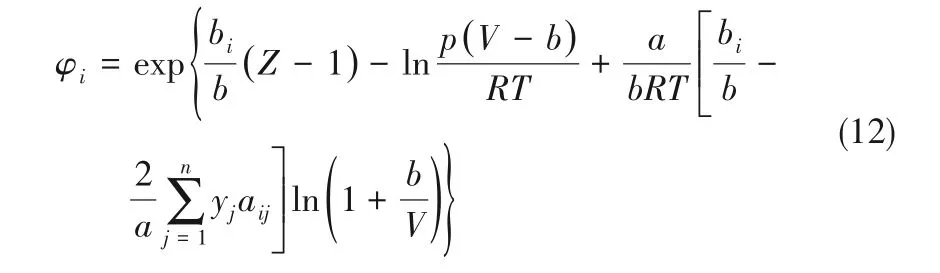
1.2 反应温度对Gibbs自由能变与反应平衡常数的影响

反应的标准摩尔焓变、标准摩尔熵变、标准摩尔Gibbs自由能变以及标准反应平衡常数采用如下方程进行计算：

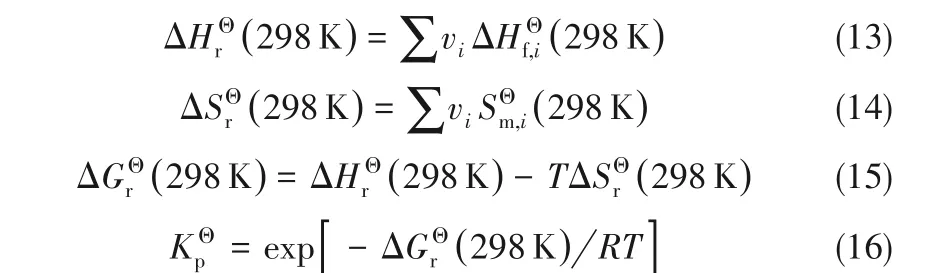
根据上述求得的标况下热力学数据，进而可以得到在不同温度下的反应标准焓变、熵变和Gibbs自由能变。其计算式如式（17）～式（19）所示。

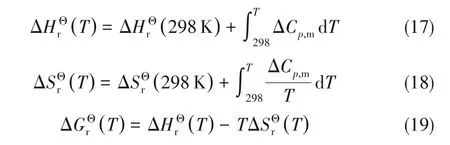
其中，ΔCp,m=∑vi Cp,i(T)。

采用上述方程计算了反应温度在400～600 K范围内的标准摩尔反应焓变、熵变、自由能变及平衡常数，其中，反应自由能变及平衡常数随温度变化情况绘制于图1中。由计算结果可知，在考察温度范围内，反应焓变（-53.49～-64.52 kJ·mol-1）、熵变（-87.25～-109.83 J·mol-1·K-1）均为负值且随温度升高而降低，即随反应温度升高，DMA加氢反应放热量增大。反应Gibbs自由能变随反应温度升高而升高，在反应温度不高于580 K时，反应Gibbs自由能变小于零，反应为自发过程，升高温度不利于该反应的自发进行。仅从热力学角度分析，降低温度有利于反应物平衡转化率的提高。然而，由Arrhenius方程可知，反应温度的降低会导致反应速率降低，因此，在实际生产过程中，反应条件的确定还需综合考虑温度对反应平衡和反应速率的影响。

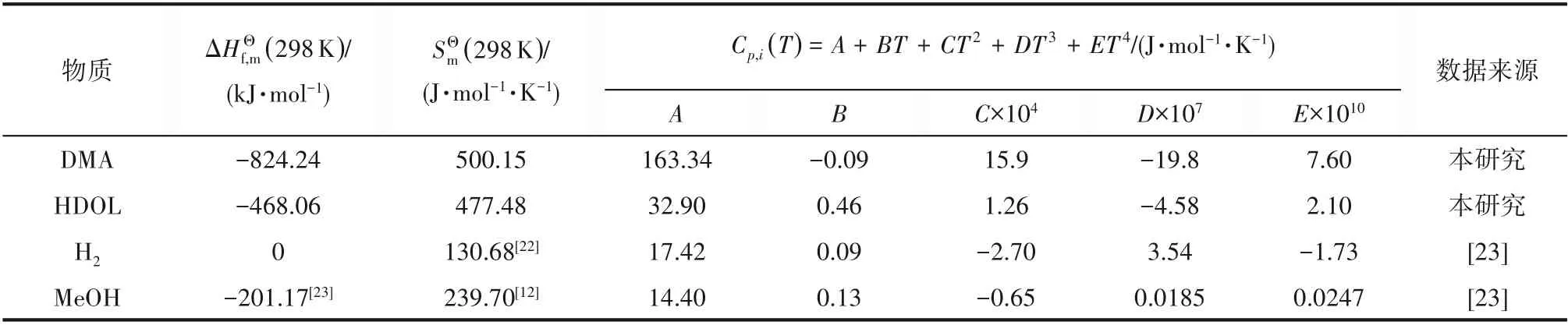
表3 各物质标准摩尔生成焓、标准摩尔熵及比定压热容关联系数Table 3 Standard molar formation enthalpy，standard molar entropy and the parameters of heat capacity of the species involved in this work

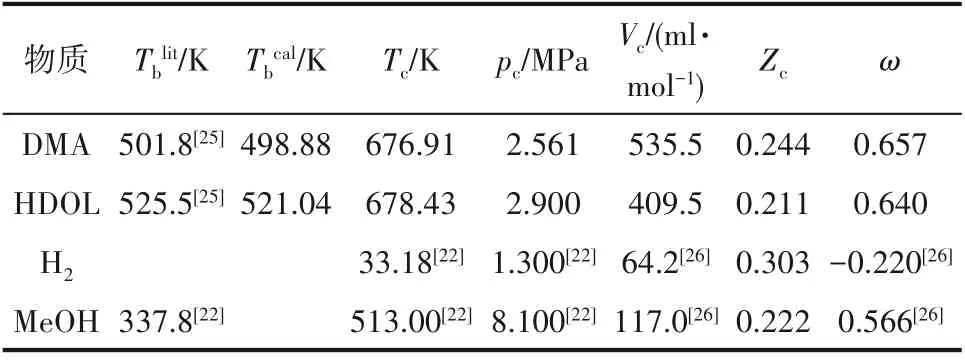
表4 各物质临界性质及偏心因子Table 4 Critical parameters and the acentric factor of species used in this work

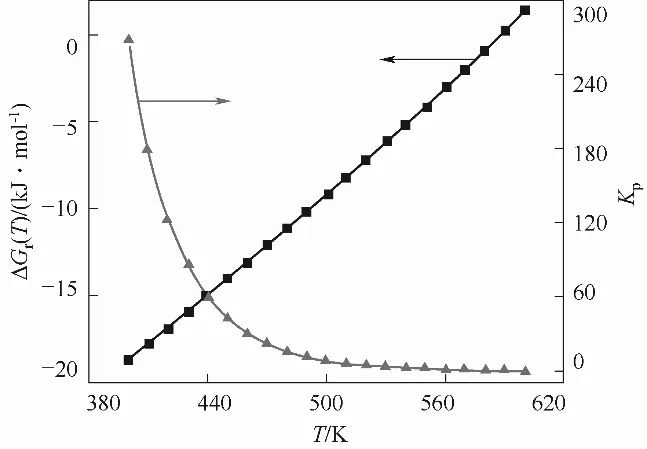
图1 不同温度下的标准摩尔反应Gibbs自由能变及平衡常数Fig.1 Curves ofΔ(T)and K p with the increases of temperature

1.3 反应压力对Gibbs自由能变和平衡常数的影响

相关文献及本课题组前期研究表明[7,27-29]，DMA加氢反应一般是在较大氢酯摩尔比（H2/DMA≥150）和较高反应压力（p≥6 MPa）下进行的。因此，在高压、高氢酯摩尔比条件下对反应体系进行热力学分析是更有现实意义和应用价值的。本文在H2/DMA=150，压力分别为2、6、10、15和20 MPa的反应条件下，在一定温度范围内对反应Gibbs自由能变和平衡常数进行计算，探究压力对反应平衡的影响。由热力学第一定律和第二定律得到的dG=Vdp-SdT，可以推导出恒温条件下Gibbs自由能变与反应压力之间的关系如下：

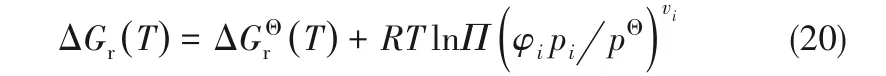
采用式（20）计算的反应Gibbs自由能变和由此得到的平衡常数绘制于图2中。由图可知，随着压力升高，DMA加氢反应Gibbs自由能变降低，反应平衡常数升高，说明高压有利于反应自发进行。在计算条件范围内，平衡常数计算结果为1.6×106～9.7×108，说明在热力学上DMA加氢转化为HDOL是可行的。此外，从图2(b)中还可以发现，温度越低，压力对平衡常数的影响越大。

1.4 氢酯摩尔比对Gibbs自由能变和平衡常数的影响

为进一步讨论氢酯摩尔比对反应平衡的影响，计算了在体系压力为6 MPa、温度为500 K条件下，氢酯摩尔比在100～650之间的反应Gibbs自由能变和反应平衡常数，结果如图3所示。由图可知，随着氢酯摩尔比的升高，反应平衡常数逐渐变大。当氢酯摩尔比由100升高至650时，反应平衡常数由8.2×107增大至3.4×109。对于化学反应来讲，在反应平衡常数不变的情况下，增大一种反应物的浓度，有利于提高其他反应物的平衡转化率。因此，在DMA加氢反应中，适当提高氢酯摩尔比，不仅有利于DMA的汽化，也有利于增大反应平衡常数和提高关键组分DMA的平衡转化率。但是，高氢酯比就意味着有更多的H2需要循环处理，这无疑会增加动力和分离等设备的运行成本。所以，在实际工业生产和实验研究中，还需综合考量，选择适宜的氢酯摩尔比。

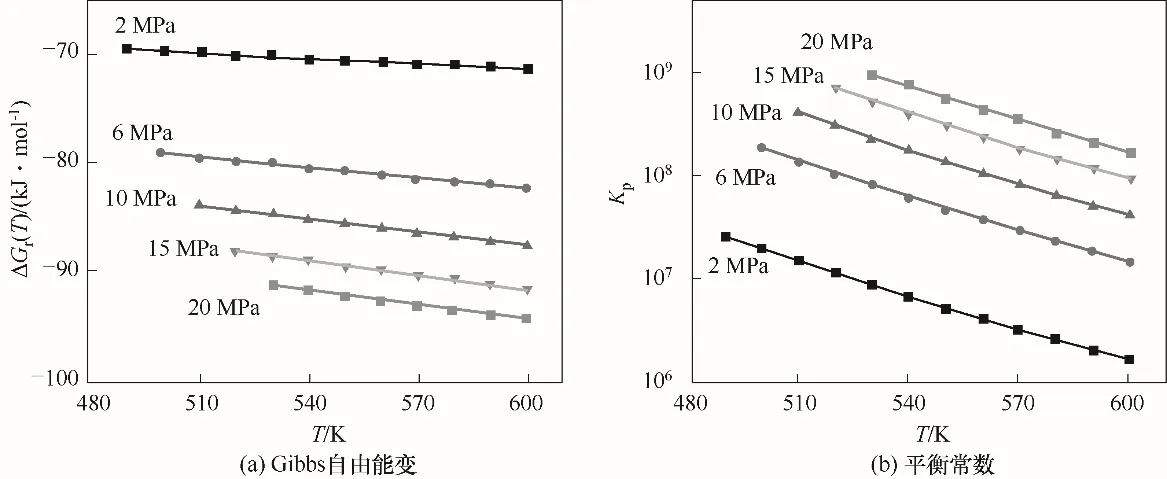
图2 不同反应压力下反应Gibbs自由能变、平衡常数与反应温度的关系Fig.2 ΔG r(T)and K p of reaction at different pressures as a function of temperature

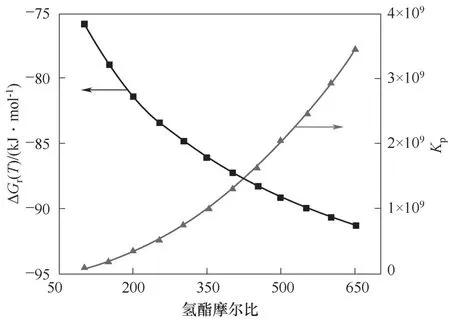
图3 氢酯摩尔比对反应Gibbs自由能变及平衡常数的影响Fig.3 Effect of molar ratio of H2/DMA onΔG r(T)and K p

1.5 平衡转化率的计算

为确定不同反应条件下混合物的状态，采用计算得到的热力学数据和RKS方程对混合物（H2/DMA=150）的露点进行计算，结果如图4(a)所示，动力学实验条件下的混合物露点温度与实验温度对比绘制于图4(b)中。由图可见，在考察条件范围内和动力学实验条件下，反应温度均高于露点温度，混合物均以气相形式存在。因此，反应平衡常数与平衡时物质组成之间的关系可用式（21）表示：

结合物料衡算可以得到反应达到平衡时各组分含量，进而求得关键组分DMA的平衡转化率。经计算，在考察压力和氢酯摩尔比范围内DMA平衡转化率均在99.99%以上，因此，在一定范围内，工艺条件的改变不会引起DMA理论平衡转化率的显著改变。此外，在本文动力学研究实验条件范围内，计算所得DMA理论平衡转化率均接近100%。

2 DMA加氢反应动力学研究

2.1 实验及分析方法

DMA加氢实验是在固定床管式反应器（青岛捷天）中进行的，反应管内径10 mm、长度600 mm、DMA和H2流量分别通过高压微量恒流泵和质量流量计控制。加氢产物经冷凝后进行气液分离，尾气排空，液体收集后利用气相色谱仪（岛津）进行定量分析。色谱条件为：进样器和检测器（FID）温度分别为250℃，色谱柱采用毛细管柱，载气为高纯氮气，流量30 ml/min。柱箱采用程序控温，程序为：初始温度50℃，保持5 min，然后以20℃/min升温至220℃，保持15 min。液相产品用无水乙醇（色谱纯）稀释后由自动进样器进样，进样量为1μl，分流比为100∶1，样品中物质含量采用外标法定量，DMA和HDOL标准曲线相关系数分别为0.99998和0.99994。每个样品至少分析3次，取其平均值作为实验结果。

2.2 内外扩散影响的消除

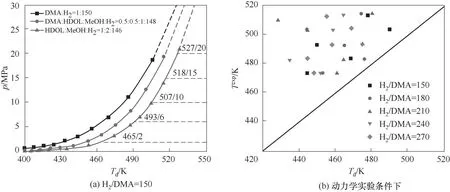
图4 混合物露点曲线Fig.4 Dew point curves of mixtures

实验采用本课题组研制的Cu/ZnO/Al2O3催化剂[7,28-29]，通过改变催化剂颗粒大小的方法，消除内扩散的影响。经模压成型、研磨筛分后，选取颗粒尺寸分别为20～40目（0.42～0.84 mm），40～60目（0.25～0.42 mm）和60～80目（0.18～0.25 mm）3种粒径的催化剂颗粒进行实验，结果如图5（a）所示。当颗粒直径为20～40目时，内扩散影响已经消除。外扩散影响可通过增大物料流速的方法消除，即在相同的气时空速条件下，改变催化剂的装填量。气体流速对DMA转化率的影响如图5（b）所示在催化剂装填量为2 g时，外扩散影响可认为已经消除。在本研究中，选用催化剂粒径为40～60目，催化剂装填量为3 g进行动力学实验。

2.3 实验设计与结果

采用正交实验设计方法，在温度为473.15～514.15 K、压力为2.0～6.1 MPa、液时空速（LHSV，DMA常温下为液体，在实验条件下为气体，为便于计算，实验采用液时空速计量）为1.28～2.55 h-1、氢酯摩尔比为150～270，进行25组动力学实验，实验结果列于表5。

2.4 动力学模型

反应产物分析结果表明，在实验条件范围内，HDOL选择性均大于95%，因此在动力学方程拟合中，忽略副反应影响。根据热力学分析结果，在动力学实验研究条件下，DMA平衡转化率均接近100%，因此反应按不可逆处理。本文选取形式较为简单、方便应用的幂函数型动力学模型[30-31]，方程形式如下：

其中，k=Aexp(-EaRT)；pDMA和pH2分别表示DMA和H2的分压，MPa；采用RKS方程分别对各组实验始、终态混合物组分逸度系数进行计算，结果表明，各物质逸度系数均接近1且变化幅度小于5%，因此在动力学方程拟合中，为方便应用，DMA和H2分压在计算时忽略逸度系数影响；a、b分别表示DMA和H2的反应级数。

表5 动力学实验结果Table 5 The results of kinetic experiments

图5 内扩散和外扩散对DMA转化率的影响Fig.5 Effect of internal and external diffusion on DMA conversion

本研究以DMA作为关键组分，以出口DMA摩尔分数作为独立变量，设定目标函数为式（23）。采用四阶Runge-Kutta法求解微分方程，通过简面体爬山法进行参数估值，得到DMA加氢动力学方程如式（24）所示，可知，反应活化能为63.55 kJ·mol-1，DMA和H2的反应级数分别为0.63和0.40。值得注意的是，根据反应方程式，1分子的DMA与4分子的H2反应，H2的反应级数应大于DMA，但是，拟合结果却与之相反。这是由于反应体系中氢酯摩尔比较高（≥150），H2分压近似等于反应压力，反应前后变化不大。在动力学方程中，H2分压项（pH2）主要反映的是反应压力对反应速率的影响。这一研究结果与相关文献报道相一致[32-34]。

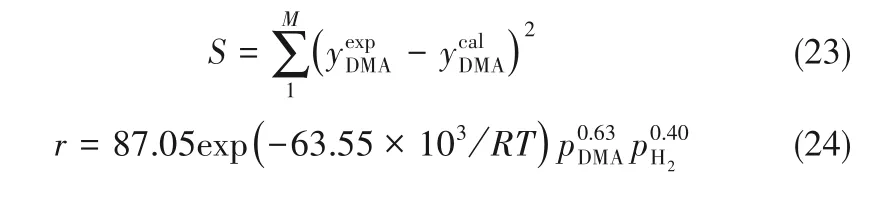
对上述动力学方程进行形式变换，可得到氢酯摩尔比为n（n=150～270）时的初始反应速率如式（25）所示。可以看到，在本实验考察条件范围内，压力对初始反应速率的影响比氢酯摩尔比更大，增大反应压力和减小氢酯摩尔比，有利于提高初始反应速率。

2.5 模型检验

反应器出口DMA含量实验值与模型计算值对比如图6所示。由图可见，模型计算值与实验值吻合度较高。对获得的动力学方程进行统计检验，结果列于表6。其中,ρ2表示决定性指标，F代表回归均方和与模型残差均方和之比[35]。由统计结果可知，ρ2＞0.99，F＞10F0.05(20,4)，表明在实验条件范围内，该动力学模型是适用的。

3结 论

（1）计算了DMA和HDOL的标准摩尔生成焓、标准熵和比定压热容，并以此得到了DMA加氢反应的Gibbs自由能变和平衡常数。在标准压力、不同反应温度下得到的反应焓变、Gibbs自由能变数据表明，该反应为放热反应，反应放热量随温度升高而升高，在400～580 K，反应Gibbs自由能变小于零，反应为自发过程，平衡常数随反应温度的升高而降低。

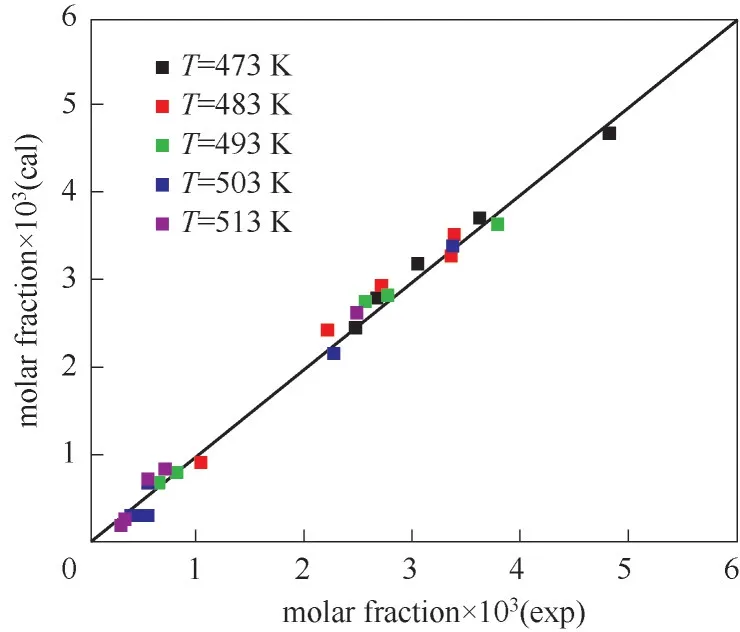
图6 反应器出口DMA摩尔分数的实验值与计算值对比Fig.6 Comparison of experimental and calculated data of molar fraction of DMA at the reactor outlet

表6 动力学方程统计学检验结果Table 6 Statistical test results of kinetic equation

（2）不同反应压力下的计算结果表明，提高反应压力和氢酯摩尔比有利于反应的正向进行，有利于提高反应平衡常数。对反应平衡转化率的计算结果表明，在所考察的工艺条件范围内，反应条件的改变不会引起DMA理论平衡转化率的显著变化，其值均在99.99%以上。在工业生产和实验研究中，DMA加氢的工艺条件在热力学上具有较大调变空间。

（3）在消除了内外扩散对反应的影响后，利用固定床高压反应器对DMA加氢动力学展开研究。采用Runge-Kutta对建立的幂函数型动力学模型进行参数估值，得到了反应的活化能为63.55 kJ·mol-1，DMA的反应级数大于H2，分别为0.63和0.40，在动力学实验条件范围内，增大反应压力和减小氢酯摩尔比有利于初始反应速率的提高。

符号说明

A——指前因子，mol·g-1·s-1·MPa-(a+b)

Cp——比定压热容，J·mol-1·K-1

Ea——反应活化能，J·mol-1

G——Gibbs自由能，kJ·mol-1

H——焓值，kJ·mol-1

Kp——反应平衡常数

k——反应速率常数，mol·g-1·s-1·MPa-(a+b)

LHSV——液时空速，h-1

M——动力学实验组数

Mp——动力学方程参数个数

NA——分子中的原子数目

Ni——基团i

Nes,Nis——分别为外部、内部不可分辨性数目

p——压力，MPa

pΘ——标准态压力，0.1 MPa

pc——临界压力，MPa

R——气体常数，8.314 J·mol-1·K-1

r——反应速率，mol·g-1·s-1

S——熵值，J·mol-1·K-1

T——温度，K

Tb——沸点，K

Tc——临界温度，K

Td——露点，K

V——混合物的摩尔体积，ml·mol-1

Vc——临界摩尔体积，ml·mol-1

v——反应计量系数

vc——临界反应计量系数

y——摩尔分数

Z——压缩因子

Zc——临界压缩因子

ω——偏心因子

φ——逸度系数

上角标

a,b——反应级数

cal——计算值

exp——实验值

lit——文献值

Θ——标准态

下角标

f——生成态

i——组分

k——基团数

m——摩尔

r——反应态