基于Memetic 算法的仿真用例集约简技术
杨祎巍,匡晓云,黄开天,洪超,郑昌立,蒋小文*
(1.广东省电力系统网络安全企业重点实验室(南方电网科学研究院有限责任公司),广东广州 510080;2.浙江大学信息与电子工程学院,浙江杭州 310027)
0 引言
回归测试集是一组达到了目标覆盖率的用例集合,一般通过制订用例计划实现或由自动随机产生的方式构造,易导致一些点被多个用例重复覆盖,造成用例冗余[1]。在回归测试时,为缩短仿真时间,提高效率,希望找到极小的用例集合,在满足覆盖率的前提下,用尽量短的时间,完成回归测试,在多次反复执行中,节省了大量时间,从而大大缩短项目完成时间。通常,对所有用例进行回归测试,只适用于规模较小或项目时间较宽松的情况[2]。有时会根据对项目的理解,凭经验从用例集中挑选一些用例进行计算,但效果并不理想,需具有与项目强相关的专业知识,通用性亦不好,当用例选择不同时,结果差别很大,且不能同时满足覆盖率和精简化的要求。
目前,在相关测试用例集约简技术中,从测试需求集或组合覆盖着手的测试方法较多。其中,组合测试有正交试验设计法和两两组合覆盖法等[3]。基于测试需求集的方法主要将约简问题抽象为数学问题,用数学方法求解。用得较多的有贪心算法、启发式算法、遗传算法以及蚁群算法等生物进化算法[4]。
在处理实际问题时,优化算法是将问题用类似的生物或数学模型代替,然后代入合适的策略进行求解。编码与解码互相对应,在算法搜索空间和实际问题的解空间之间进行转换[5]。相较于其他进化算法,Memetic 算法在求解中增加了局部处理步骤,其作用是对全局处理后的个体做局部处理,在一些位置做突变,尽早将一些不好的个体筛除,从而减少运算次数,提升运算效率。影响Memetic 算法的关键因素是各算子的选择和局部策略的性能[6]。
1 用例集约简模型
分析测试用例集的特点发现,其与集合覆盖问题的数学描述相似,可将约简测试用例集的求解问题转换为集合覆盖问题的优化求解。集合覆盖问题在日常生活中较常见,是一类带有约束的离散优化问题,其变量和解一般为整数向量,如调度问题、选址问题等,是一类非确定多项(non-deterministic polynomial,NP)难问题。通俗讲,集合覆盖问题可解释为:有2 个集合E和S,S中元素能全部覆盖E中元素,如果S中有n个子集,每个子集对应一个耗费代价,在S的子集中能找到完全覆盖集合E的集合,且耗费代价最小[7]。集合覆盖示意如图1 所示。测试用例集约简问题,则是全部的功能覆盖点集合E(为需要被覆盖的集合),各用例组成的测试用例集为集合S,子集中每包含一个测试用例,其耗费代价将相应增加,在完全覆盖所有被要求覆盖的点的条件下,选择耗费代价最小的子集,即测试用例集数量最少的集合。

图1 集合覆盖问题示意Fig.1 The model of test case suite reduction
假设有i个行元素的整体,代表所有需要覆盖的功能点,有j个列元素的整体,代表所有用例集合,用式(1)表示,其中,xj表示用例集中第j个用例是否被选择组成子集,xj是一个二值元素(取0 或1),取1 时说明第j个用例被选中,加入约简用例组合,取0 时说明第j个用例未被选中;tj表示每个用例所需的仿真时间,aij表示第j个用例是否覆盖第i个功能点;cj表示每个用例的耗费代价,在本文的约简问题中,cj=1。

2 Memetic 算法
2.1 种群编码及初始化
在测试用例约简问题中,采用二进制编码,每比特有2 种取值,分别表示用例的选择与否。通过此方式,有n个用例的用例集用一个n位的二进制串表示,每位对应一个用例,其值反映用例是否被选择。
种群的数量是种群初始化的重要参数,对算法的运算性能有一定影响。为使计算量不至于过大、多样性不会太低,通常选择种群数量为20~100[8]。本文选取的种群数量为50,即每代种群中有50 种不同的用例集组合。
由于在本文的约简问题中有一些约束条件,不满足约束条件的个体得到的是不可行解。当不可行解较多时,从不可行解区域收敛至可行解区域会浪费较多时间。本文采用贪心策略,如图2 所示,在随机产生的种群数量个体中,将所有用例按适应度函数值从大到小排列。在种群初始化后,检查初始化种群个体,若发现其为不可行解,则添加适应度值大的用例使其变为可行解。
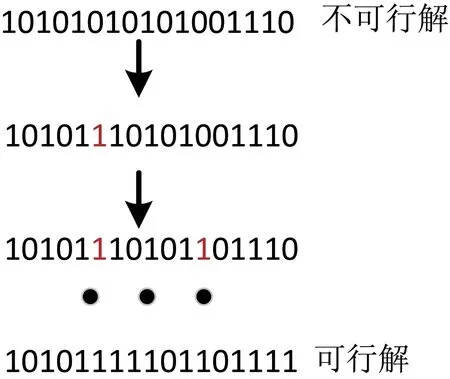
图2 贪心修正策略Fig.2 The greedy correction strategy
2.2 适应度函数
为使结果尽可能快速地向可行解区域收敛,将约束处理机制融入适应度函数设计,并与后续的选择策略相结合。当个体满足约束条件时,仿真时间较少的个体比仿真时间较多的个体优先被选中,当仿真时间相同时,用例集较小的个体优先被选中。对可行解,计算每个个体的用例数与全部用例数的差与时间相关的数值和,并将其作为适应度函数,对非可行解,用两者的差值与时间参数值的和表示适应度值,并令非可行解的适应度函数值均小于0,令可行解的适应度函数值均大于0。

其中,n为原始用例集的用例数,gij为当前种群第i个个体X的第j位,总和即为用例集数,t(X)表示某个体代表的用例集运行的仿真时间,T表示原始用例集运行的仿真时间,cov(X)表示个体X的覆盖率,cov(I)表示原始用例集的覆盖率。
2.3 全局搜索策略
在设计全局搜索策略时,将遗传算法和差分进化算法相结合,整体架构以差分进化算法为基础。在初始化种群后,采用差分进化算法运行步骤,先变异、交叉,然后选择如图3 所示的混合全局搜索策略。

图3 混合全局搜索策略Fig.3 The hybrid global strategy
由于差分进化的变异算子在实数域上,而本文讨论的离散问题在实数域上搜索无效果,因此,首先,须采用遗传算法中的变异算子处理二进制数据串,然后,由差分进化的交叉算子产生中间代种群,最后,在中间代种群与原始种群间做选择。
2.3.1 变异算子
变异策略是全局策略中的重要操作,亦是保证种群多样性的关键步骤,与染色体的编码方式息息相关。本文采用的编码变异方法具体表现为二进制串每个基因位上的数值在0 和1 间翻转。对传统一元变异充分性不足问题,用2 个基因位结合使用的方法解决,如图4 所示,对2 条染色体采用二元变异操作,效果明显好于一元变异[2]。

图4 二元变异Fig.4 The binary variation
在本文设计的变异策略中,同时使用同或和异或2 种运算,2 个旧个体产生2 条新染色体,如此,每个基因位均为原来的0 和1,仅染色体组合不同,使得种群变化足够丰富,同时保证了基因完整性。进行变异运算时,先将输入的种群个体打乱,随机排序,每次取相邻的2 个个体做二元变异,n个个体种群就有n/2 个子集。
2.3.2 交叉算子
通常,交叉策略用得较多的为二项交叉和指数交叉2 种。受文献[9]启发,本文采用动态调整的方式,在种群更新中,每次迭代后更新交叉率。交叉率值(CR)由均值a和标准偏差决定,随着种群的更新,均值a也相应更新,以适应不同进化阶段的特性。同时,随适应度变化做动态调整,当适应度较小时增大交叉率,较大时适当减小交叉率,使其尽快收敛。

其中,c为0~1 的常数,fmax表示当前种群最大的适应度,f′表示完全用例集的适应度。更新a之后,即可根据正态分布得到种群个体数量的CR 值,即scr列表,每个个体对应一个值。mean(scr)为Lehmer平均值,计算式为
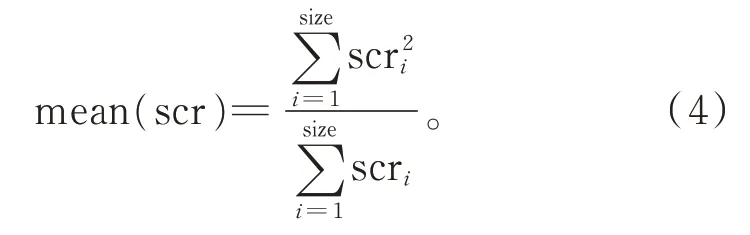
2.3.3 选择策略
以差分进化算法中常用的贪婪选择方式为选择策略,初始化后通过变异和交叉操作得到中间代种群,然后比较原始种群与中间代种群。在选择策略中,比较原始种群与中间代种群对应个体的适应度值,适应度大的个体加入新的种群,如式(5)所示。
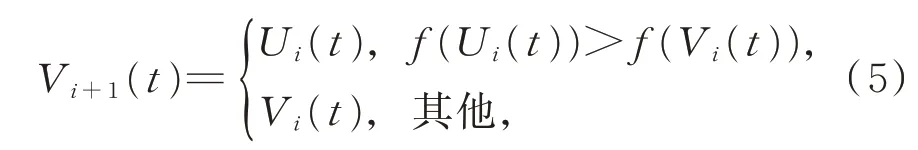
其中,Vi+1(t)为新一代种群的第t个个体,Ui(t)和Vi(t)分别为中间代个体与当前代个体。
2.4 局部搜索策略
在常见的几种局部搜索策略中,禁忌搜索的局部寻优能力最强[10],为此,本文采用禁忌搜索策略。在完成全局策略的变异和交叉算子运算后进行局部搜索。禁忌搜索策略一般流程如图5 所示。
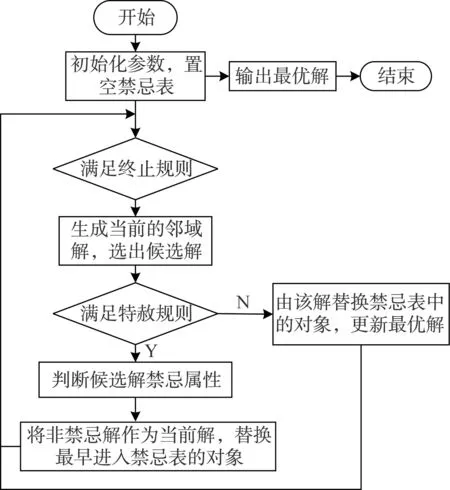
图5 禁忌搜索策略一般流程Fig.5 The general process of taboo search strategy
禁忌搜索中的关键因素有:禁忌长度、候选解、终止准则、禁忌对象、邻域结构、特赦准则等[11-12]。结合本文的测试用例集约简问题,对禁忌搜索策略做一定改进。在Memetic 算法中,局部搜索通常需多次运算,每次迭代时间虽较单独的全局搜索策略稍长,但因其迭代次数更少,所需总时间较少。本文中,因为最终的约简集合为最优个体所代表的用例集,所以应保证最优个体不陷入局部最优解,同时为减少计算用时,在全局搜索后,选取在种群中适应度排名前10%的个体,用局部搜索更新这些个体。其中禁忌长度设为5,邻域操作为随机翻转某两比特位,每次产生6 个邻域解,循环10 次,结束。
3 实验与分析
在完成上述算法设计后,进行实验分析。实验平台为基于通用验证方法学(universal verification methodology,UVM)的仿真验证平台,如图6 所示。设计模块为一款软硬件可配置的串行接口IP(RPC),串口协议特性如表1 所示,为可灵活配置的面积优化的串行协议控制器,通过状态机编程可使用不同的协议。该IP 支持配置为I2C、SPI 的主机或从机模式及标准UART 接口,此外,也可配置非标准接口。

表1 串口协议特性Table 1 The serial protocol features

图6 实验平台架构Fig.6 The experimental platform architecture
以I2C 为实验对象,以选定的用例集所能覆盖的功能点为全集,从回归测试集中选取5 组不同规模的用例集,分别运用标准遗传算法和本文的Memetic 算法进行约简实验。实验比较了约简后的用例集规模、约简过程算法运行时间、约简后用例集的仿真时间。表2 为不同规模用例集约简结果,其趋势图如图7 所示,由图7 可知,Memetic 算法较标准遗传算法的约简效果更好。表3 为在不同规模用例集下不同算法约简的运行时间,图8 为其总体趋势,由图8 可知,Memetic 算法比标准遗传算法的运行时间更少,速度更快。表4 为不同规模用例集下不同算法约简的仿真时间比较,图9 为其直方图。综上可知,本文算法约简效果更好,时间更节省,测试代价降低更显著。

表2 不同规模用例集约简结果Table 2 The results of test case suite reduction for different scales

表3 不同规模用例集下不同算法约简的运行时间Table 3 The runtime of different algorithm in test case suite reduction for different scales

图7 用例集约简结果Fig.7 The results of test case suite reduction

图8 用例集约简运行时间Fig.8 The run time of test case suite reduction

表4 不同规模用例集下不同算法约简的仿真时间Table 4 The simulation time of different algorithm in test case suit reduction for different scale

图9 用例集仿真时间Fig.9 The simulation time of test case suite
4 结论
在调研用例集约简技术的基础上,首先,对约简问题进行了数学建模。然后,根据模型特点建立了Memetic 算法,对其中的全局策略和局部策略进行了设计,研究了改进算法中的各个算子,并将其应用于约简优化问题。对于用例集约简实验,在实际项目基础上,设计了相应的UVM 仿真验证平台,形成了用例集,并对其进行仿真分析,达到了覆盖率要求,形成统一覆盖率库。最后,分别应用标准遗传算法和本文Memetic 算法对用例集进行约简实验,结果表明,本文算法性能更优、更节省时间、约简效果更显著,具有较好的实际应用价值。

