数学教育对随班就读生主动融合行为的影响

杨震 余虹

摘要：数学源于生活，高于生活。追寻人类对数学探索的足迹，结合人类對自身思维客观性认识的发展，对随班就读智障生的数学教育进行实验设计，如数学教育的综合补偿、类比教学、小导师助学等。在随班就读生的内因与外因相互作用中，探寻对该类学生数学教育的内在支撑模式，在不断实践中反思该类数学教育存在的终极意义。通过量性与质性研究得出：数学能力的提升对促进随班就读生的自我认识和主动融合行为具有显著作用。

关键字：数学教育 随班就读智障生 主动融合行为

随班就读已成为今后一定时期内特殊教育的主要形式之一。随班就读能为智障学生提供“最少限制的社会环境”，使他们成为集体成员，有机会和同龄学生在互动过程中被动与主动地尊重与理解，促进其和谐、共同发展。由于身心缺陷导致低认知水平，这些特殊学生不能与普通学生同步学习，在集体生活中始终处于劣势地位，游离于班级边缘，易产生自卑、恐惧、焦虑等心理，行为退缩，主观上缺乏主动融合意识，学校生活质量低劣不利于其长、短期发展。

挖掘随班就读生的兴趣爱好和特长优势，落足现状、长远规划，补偿能力，体验成功，激发其继续学习的信心，提升其主动融合意识势在必行。以下谈数学教育对提升随班就读生主动融合行为的影响：

一、估内因，评随班就读价值与趋势

评估随班就读生心理、行为特点，能力内涵。以建立与广阔社会生活系统相关联，以生活经验为生长点，多方整合观下的随班就读生数学教育模式。

（一）早期发现特殊学生存在的问题

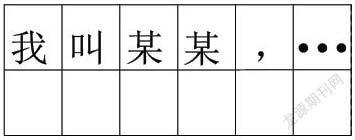
如右表随班就读生只能就近化将字词上下对应填入相邻空格（不考虑笔画错误）。但当抄写含89个字的段落时，出现标点全漏，前后颠倒，重复抄写等情况，平均连续抄写正确字数6.8个;平均漏字7.3个（均不计笔画、标点、重复、颠倒等问题）。提示瞬时记忆，注意广度，理解能力严重障碍;视觉范围狭隘，对此设法训练指正不能改善，注意力要求已超出其注意阈限。

（二）对随班就读生前期个别化评估：

1.语言功能、动作、认知测评：语言发展迟缓，言语理解困难，言语表达存在障碍。课内无法互动，无法完成正常作业;物品、颜色、空间、形状、因果、数学等概念均严重滞后，缺乏独立性和批判性。

2.知觉、学习态度与韦氏儿童智力量表测评：感知觉速度十分缓慢，注意力很容易分散，注意的持续时间非常短暂，学习和活动中缺乏主动性和坚持性。思维发展停留在前运演阶段，抽象概括能力非常薄弱，思维刻板。

根据就近发展区原则，降低教育内容的深度、广度;依据智能多元化理论，实现自身潜能开发。充分发挥数学教育作用，补偿随班就读生能力缺陷;避免隔离教育对学生成长的抑制与异化，避免教育者认识论与方法论不当导致的主观伤害;使其主动意识到对社会的贡献是实现自身价值的唯一途径，避免自我意识的缺失，而沦为寄生社会的附庸;尽可能减少由于人的社会属性而造成被歧视、排斥及物化为工具的可能。

二、究根源，定数学教育目标与策略

长、短期目标的设计，需从抽象、具象两方面解析数学教学内容，深度分析随班就读生思维方式，对数学教育目标细分定位、动态调适，筛选合理教学策略，分层次、阶段设置教育课程。

（一）溯概念由来，促协调发展

以下结合数学史角度，以随班就读生计数教育为例，阐述教师对数学教育目标深度理解与学生缺陷补偿干预的密切联系：

部分智障学生可以凭着记忆数到10，但是仅能计数出1或2或3个物品，甚至无法计数。若让他们数一组3个以上的物品，他们会表现出下述行为：同一物体重复数;另一物体被漏掉而没有数到;一次点一块不同的物体但所说的数词顺序不正确。对其中原因的探究：

对皮亚诺公理系统核心内容产生过程作分析：

定义 一个非空集合N的元素叫做自然数，如果N的元素间有一个基本关系“后继”（用符号“'’”表示），并满足下列公理：

1.1∈N，对任意a∈N，a'≠1

2.对任何a∈N，有唯一的后继元素a'（即a=b ⇒a'=b'）

3.1以外的任何元素，只能是一个元素的后继元素（即a'=b'⇒a=b）

4.（归纳公理）若M⊆N，且1∈M;a∈M⇒a'∈M，则M=N.

显然，这是从许多互不相同甚至相互排斥的实物中抽象出共性部分而成的抽象概念。意念始于具象，首先呈现于大脑中的，应该是那些熟悉的感觉对象，经过漫长的提炼过程，逐渐形成数的概念。推得自然数概念发生发展过程与随班就读生概念建构存在密切联系。

查阅数学史料，可以推知自然数概念产生与数前概念（一一对应、比较及顺序关系）以及基准数1之间的关系密切。有时顿悟亦不可少，例如某些学生肯定注意到一个苹果，二个苹果，三个苹果，···之间，多与少的不同以及集合内部每个苹果各不相同（否则与公理（2）矛盾），将他们的意念用符号表达出来即：1<（1+1）<（1+1+1）<···，认为，学生最初以个别、具体的知觉表象形式，接受与识别信息。至于抽象概念，未经训练的随班就读生不可能自主建构。部分随班就读生能建构少量抽象概念，是合理引导，强化运用，最终转化为长时记忆的结果。

因此在强化数前概念以及基准数1的建构基础上，使学生理解计数必要条件：

1.一个数词对应于同一集合内区别于其他的一个物品

2.将同一集合内物品总体按规律排列

3.按正确顺序数出数词，即1，2，3，···

4.理解概念：最后数出的数代表该集合内物品总量，即理解“1”指1个具体的事物，“2”指2个具体的事物，以此类推。

进一步需强调自然数概念的外延：比较不同物品的相同数量，如两个苹果、两名儿童和两把椅子，认识到无论具体物品是什么，只要它们的数量为2就可以数字2来表示，以此学生通过比较拓展体验，加深理解。

通过以上计数教学，对随班就读生手、眼、语言、记忆之间的协调性亦能起补偿作用。

（二）用类比推理，彰思维模式

波利亚认为在数学发现中类比推理是主要作用之一。随班就读生往往可以通过类比教学与合理的教学表征，检索已建构的概念，实现对类比目标的理解，进而建构新概念。而类比与映射有密切的关系。下面以“符号法则”教学为例，阐述类比教学对随班就读生思维拓展的价值：

1.“符号法则”的形式化证明

环R中有唯一的零元素0;对环中每个元素a都有唯一的负元素-a使a+（-a）=0。对环中元素a可以定义倍数na（n为整数），并且有：n（a+b）=na+nb;（n+m）a=na+ma;n（ma）=（nm）a。由分配律可以证明：a0=0a=0;a（-b）=（-a）b=-ab;（-a）（-b）=ab。

2.对随班就读生的“符号法则”类比教学：

（1）类比映射的建立：亏损6元用（-6）元表示，不亏不盈用（-0）元表示，则-（-6）元表示什么意思？

（2）引导学生建构预备概念：矛盾律（一个命题不能同时是真的又是假的）;排中律（一个命题或是真的，或是假的，二者必居其一）

（3）顿悟解决问题：形式上进行比较，发现（-6）元与-（-6）元含义不可能相同，即-（-6）元不可能表示亏损6元的意思，故含义只能与亏损6元相反，表示盈利6元的意思。

（4）问题的迁移：说出（-6）与-（-6）的区别; 6-2=4，则6-（-2）=？

这是令人印象深刻的案例，其中一个智障学生很快得出答案，但无法表达思考过程，推测该生已主动或被动建构类似于矛盾律与排中律逻辑原理，并自觉地应用到生活中。推测依据：当学生答错的判断题被指出后，不假思索地将错误判断修改为正确判断。

“教，然后知困，知困，然后能自强也，故曰：教学相长也”，教育者应反思数学教育对随班就读生的终极价值：引导学生在特定的环境中进行自我的内在观照，寻求精神上的寄托和满足。

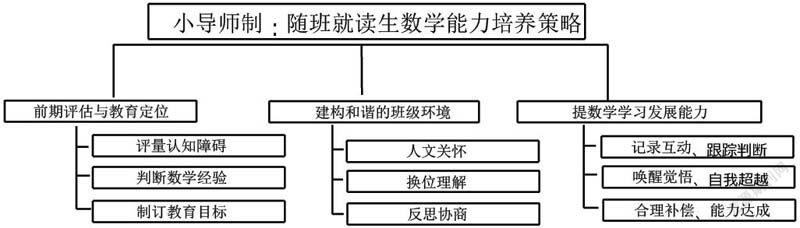
（三）试小导师制，强数学交流

在班中挑选有爱心、细心、耐心的学生建构小导师团队，在教师指导下，形成相应的指导思想、规范模式，针对随班就读生的特异化差异，制定长、短期目标，利用教具、强化、代币制等干预手段，指导其数学学习，发掘其内在潜能：

同时，设计评量观察表，收集、记录随班就读生数学能力和主动融合行为发展变化材料或教师、同伴相关评价材料及其他相关证据，为小导师辅导实效分析提供现实依据。如：活动评量观察表

經实践，小导师团队轮换进行“一对一”辅助，借助教辅具，融合信息技术，采用“小步子、大循环”方式，利于随班就读生与同伴间的平等交流与互动，发展其身心机能，补偿行为、心理缺陷。能逐步增强随班就读生数学能力，为融合教育提供内在支持和外部氛围。一定程度上弥补了教师精力短板。

但囿于小导师能力所限，存在诸多不足，如：观察不够到位;判断不够精确;教法不够灵活等。以教具使用为例：如小导师在用“蒙式教具数字拼板”教学时认为已经教会其数与点的对应关系，然而要求其给定数字取出对应数量的实物时依旧不会。此教具意图强化数字与点数间的对应关系，而拼嵌因素成为干扰项，学生将其当成拼嵌玩具，对数与点的对应关系视而不见，因此需将教具改成长方形，去除拼嵌干扰;又如使用“蒙式教具金黄串珠组”教学时，小导师对“逢十进一” 内容不能进行操作性教学，对此教具加以改进（根据映射原理将个位对应最多容纳九颗珠子的小盒子;以十颗珠子为一串，十位对应最多容纳九串珠子的较大盒子;以十串为一捆，百位对应最多容纳九捆珠子的大盒子…，以此类推）。

要用持续发展的眼光对教具加以改进、设计。教师更应指导小导师综合各种教育方式促进随班就读生对数学概念的精准理解。

三、促融合，析数学教育量与质效应

（一）实验效果的目视分析

研究对象：智力障碍随班就读生

目标行为：数学教育干预下的主动融合行为

研究设计：用单一被试研究法中的撤回设计，包含以下几个阶段：

1.基线期。该生行为资料在基线期收集完成，并显示该生的行为出现频率。在基线期稳定后则进入干预期。

2.干预期。实施行为干预计划，直到达成预定的目标。

3.追踪期。保留符合自然情境下出现的策略，撤除行为干预计划，以了解行为支持计划对该生问题行为的影响。

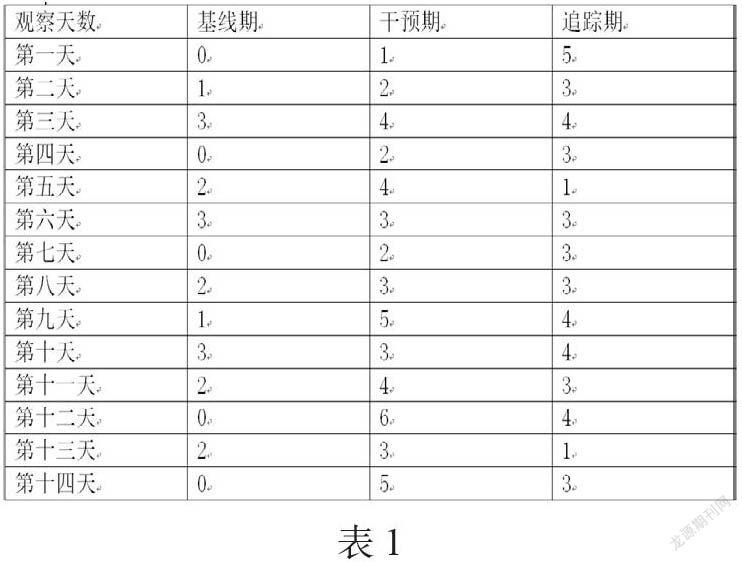
个案主动融合行为次数各阶段数据如表1。研究结果与分析：

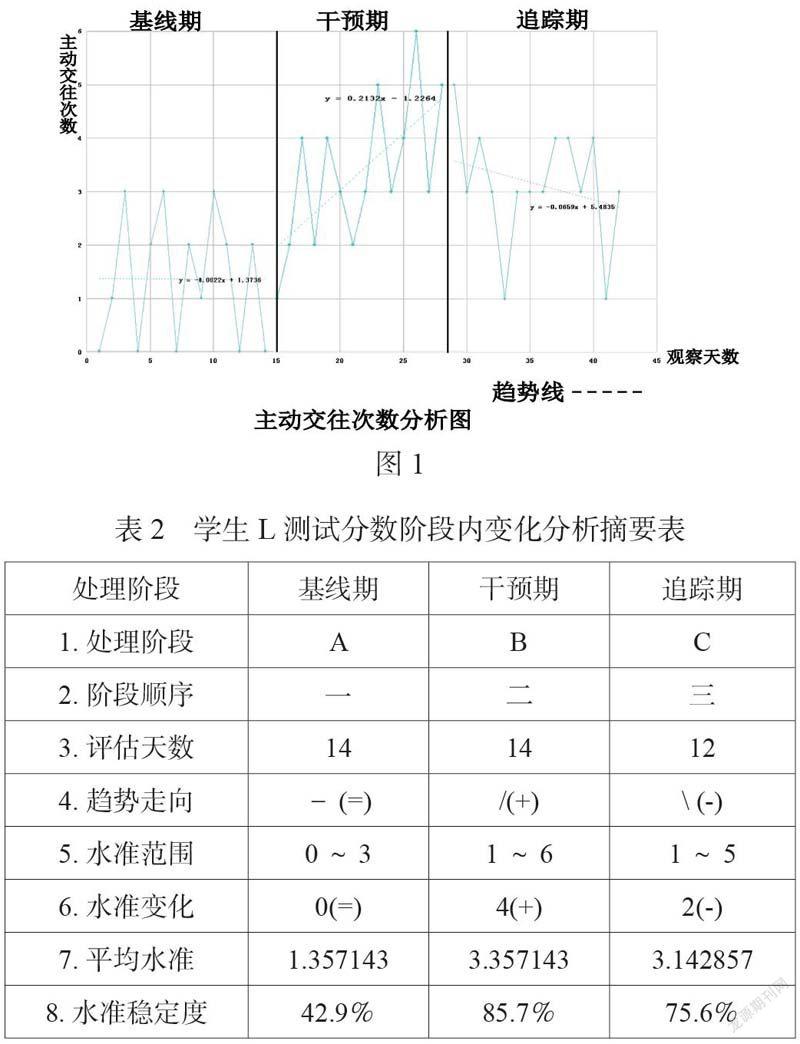
阶段内的目视分析：个案测试分数在基线期、干预期与追踪期的阶段内

变化如图1，分析摘要如表2。

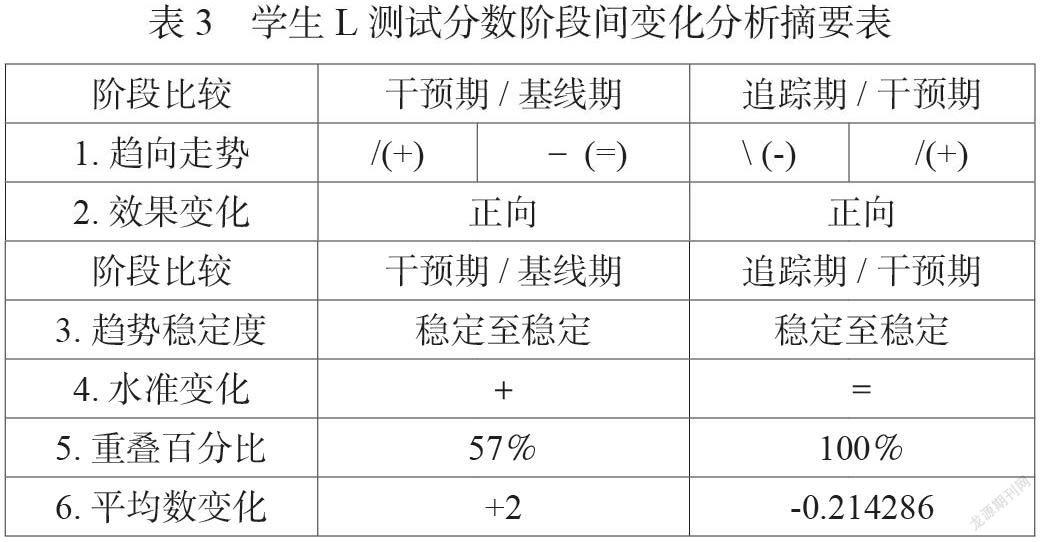
2. 阶段间变化：个案问题行为阶段间变化分析摘要表如表3

经视觉分析，可知基线期、追踪期、干预期三阶段内主动融合性行为次数相差似乎不大，学生L经过行为干预后平均水准从1.357143上升至3.357143，在干预期间，其主动融合性行为次数呈正向递增的趋势，且追踪期基本维持干预期中的成效，平均水准仍为稳定状态。

（二）数理统计的干预分析

对表1的个案主动融合行为次数各阶段数据进行分析：

1.各期数据自相关检验：由以上倒反设计实验，基线期Br=-0.74267;干预期Br=0.006435;观察期Br=-0.12148，得各组数据非自我相关。

2.对三组数据F检验： F（2，39）=5.18，故P<0.01，差异显著。

3.N-K检验法：当r=2时，q0.05·=0.9492;当r=3时，q0.05·=1.1417;X3-X1：r=3时1.7858>1.1417存在显著差异性;X2-X1：r=2时 2>0.9492存在显著差异;X2-X3：r=2时0.2143<0.9492无显著差异。多重比较结果表明，实施行为干预能有效增加个案的主动融合性行为;撤除干预后主动融合性行为次数略有下降，但明显高于干预前水平。

综上得，数学的客观性与抽象性，建立在实践基础之上，数学体系的建立体现了人的主观能动性。对随班就读生的数学教育更要注重实践，促其多方体验、感悟生活、增加阅历，为其潜能的激发提供条件。唤醒随班就读生自我意识，促其自我超越与建构，增强社会归属感，提升认识与改造外界事物的能动性，最终为其主动融合社会奠定基础。

参考文献

[1]张厚粲，徐建平.现代心理与教育统计学[M].北京：北京师范大学出版社，2014.10.

[2]戴晓阳.常用心理评估量表手册（修订版）[M].北京：人民军医出版社，2015.10.

[3]李文林.数学史教程[M].北京：高等教育出版社;海德堡：施普林格出版社，1999.8（2002重印）.

浙江省桐乡市特殊教育学校

桐乡市濮院小学教育集团毛衫城小学