印尼高中数学教科书内容及结构变化研究

王奋平 Nuraeni Ratna Sari

【摘 要】 和中国一样，印度尼西亚正在进行高中数学课程改革，高中数学教科书也随之不断进行修订和完善，教科书内容和编写风格、编写模式的变化体现了该国教育思想的变化.和2006版高中数学教科书相比，印尼2013版高中数学教科书内容大幅减少，但是更加注重“解决问题”导向的数学学习模式，注重将数学知识融入情境问题中，学习主题深度加深，各主题知识范围也扩大了.

【关键词】 印度尼西亚;高中数学;理科教科书;比较

近些年，数学教科书的国际比较研究是我国数学教育研究领域的一个热点，尤其是对西方发达国家与中国中小学数学教科书的研究较多，但是对于印度尼西亚（以下简称为印尼）的数学教科书研究较少，印尼小学六年，初、高中各3年，大学3至7 年.实施中学教育的机构有普通中学与职业中学两类，为继续升学或者就业做准备.和世界上很多国家一样，印尼高中阶段数学学科也要按照社会科学（中国一般称为文科）和自然科学（中国一般称为理科）来分类学习.印尼高中现在正在使用的两种高中数学教科书是依据两个不同版本的课程大纲作为编写的，一个是依据2006年版的《高中数学课程大纲》编写的教科书，本文简称为2006版教科书，另一个依据是2013年版《高中数学课程大纲》（2016年做了修订）编写的教科书，简称为2013版教科书.第一个版本的教科书正在逐步退出市场，而第二个版本的教科书已经逐渐占主流，该系列教科书主要在2017—2018年间出版.本研究将依据对这两种版本的理科数学教科书内容和结构加以比较研究，以期对正在进行改革的中国高中数学教科书带来一些思考.

1 印尼两种高中理科数学教科书内容比较

1.1 印尼高中理科数学教科书内容比较

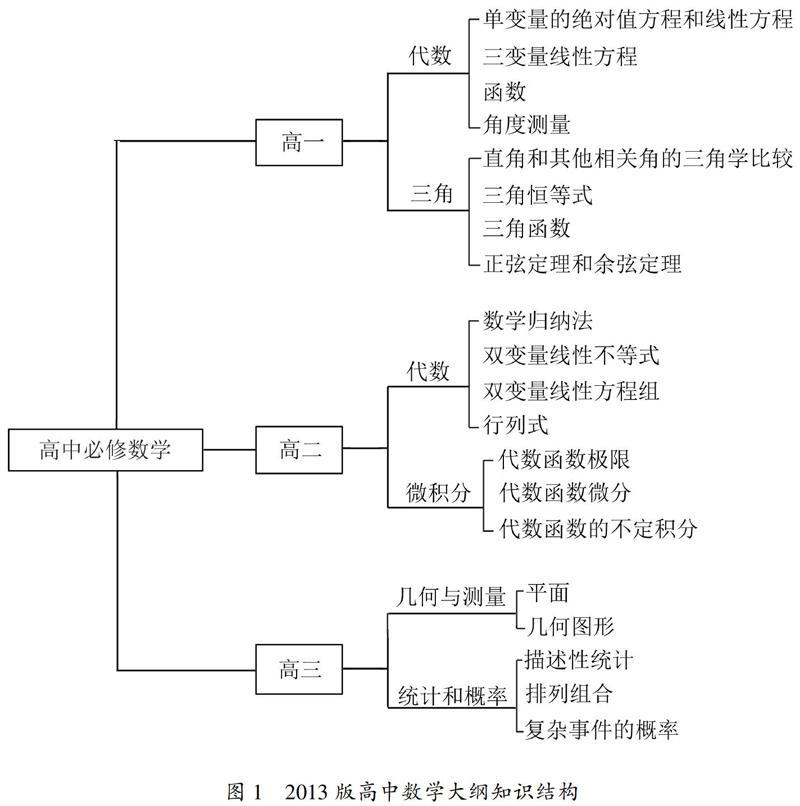
无论2006年版理科教科书还是2013版理科教科书均由教育和文化部协调并组织相关方面审查，2013版教科书还在初期阶段试用，要根据社会需求的动态不断进行改进、更新，2013版高中三个年级的教科书并不是同时出版的，本研究所使用的2006版教科书由Yrama Widya出版公司组织编写出版，经印尼教育和文化部审核通过，2013版教科书高一年级、高二年级教科书2017年出版，高三年级教科书2018年出版，均为印尼教育和文化部主持编写的部编教科书.根据印尼教育和文化部2013年颁布的高中数学课程大纲，高中各年级应该学习的主要内容分布状况如图1.

印尼2006年版高中理科数学教科书内容和中国大陆上世纪1980年到2002年新课程改革前的教科书内容很相似.只是中国上世纪80年代的高中数学教科书没有印尼教科书中的矩阵内容，印尼教科书中内没有中国上世纪80年代教科书中的立体几何内容.与2006年版高中数学教科书内容相比，印尼2013年版高中数学教科书内容发生了很大变化.

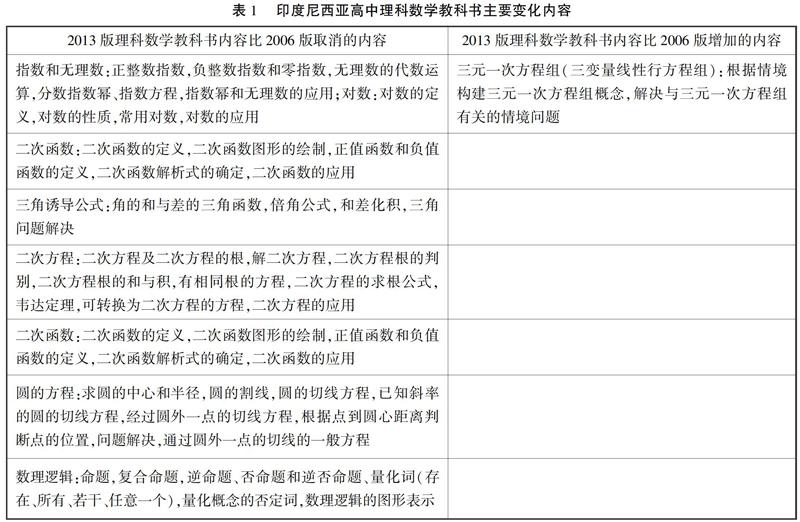
从印尼两个版本教科书内容看，均包含代数、 三角函数、几何和测量、统计和概率、 微积分五个模块的知识.但是新旧版教科书内容变化很大，2013版教科书内容比2006版教科书少了很多，说明2013版数学大纲本身要求学习的数学内容减少了.其中二次方程、二次函数等内容只是调整到初中学习了，和中国高中数学课程改革一样，印尼2016版教科书取消了指数方程、对数方程、数理逻辑、圆的方程等多块内容，对照2013版教科书内容，该系列教科书基本上是严格按照2013版数学大纲要求的学习内容编写的.

1.2 印尼高中理科数学教科书编写结构比较

印尼2006年教科书每节的知识呈现结构图：

各章每节编写结构几乎一样，没有章学习目标、节学习目标、也没有章总结.每章最后虽有一节为章测试题，但是因为缺少较为明确的章核心概念结构图谱，只通过测试题对本章内容的归纳和总结效果是有限的.

印尼2013年版各章结构图中的主要因素如图所示：

每一章章末都有一个章总结环节，对本章内容进行概括.2013版教科书每一章有专门的知识储备要求：“基本能力和学习经验”，还有本章“知识结构图”供学生提前了解本章基本概念及各概念之间的关系，另外还提供学习用参考资料：“学习资料”供学生扩展视野.尤其是高三教科书最后一章的“综合能力培养”，是综合应用高中三年的教科书中学习过的数学知识解决综合性的问题，所涉及数学知识涵盖面广.高三教科书最后一章“综合能力培养”中包括：使用正弦和余弦定理以及几何变换性质分析平面图形之间的相似性和全等关系;使用正弦和余弦定理以及几何变换性质解决平面图形之间的相似性和一致性有关的问题.可见，2013版教科书更加注重学习过程，注重情境教学，重视学生自我探究，重视学习效果评价.

2 研究結论

2.1 印尼新教科书大幅度减少数学学习主题

从表1所列印尼新、旧教科书的内容看，2013版数学教科书的内容远远少于2006版数学教科书内容，和中国大陆基础教育阶段数学课程学习内容方面的改革方式不谋而合，中国大陆自上世纪末开始的基础教育阶段数学课程改革中为了减轻学生学习负担、适应社会对数学的现实需求而减少或取消了所谓“繁、难、偏、旧”的内容，印尼2013版高中数学教科书和2006版相比，其内容减少了指数方程、对数方程、数理逻辑、向量、解析几何中圆的方程、三角恒等式等内容，减少的内容大致和上世纪末开始的中国基础教育数学课程改革新教科书所作的变动相同.根据印尼2013版《高中数学课程大纲》的表述：

（要让数学）易教（可教）;易学（可学的）;可衡量（测量）;有意义的学习（有价值）.

为了达到上述目标，适度减少数学学习内容是其中一条途径.虽然减少了数学学习主题，但是增加了每个主题的容量.这样的方式必然增加例题、习题数量，自然也加深了每个主题的深度，拓宽了该主题的范围，有利于更全面、更深刻地掌握所学数学主题.如果说取消上述内容是因为“难度过大”，那么取消向量就很难理解其原因了，因为向量在应用型学科中有很重要的工具作用，即使在初等数学以及中学物理的学习中也有很重要的作用.

2.2 新教科书重视知识图谱对学生数学知识理解的促进作用

不同于2006版教科书，印尼2013版教科书在每本教科书目录后附有本书的知识结构图，每章章首也均绘制了本章主要知识点及其之间的逻辑关系图，例如在高一第三章三元线性方程组中，就有一个直观的概念结构图：方程→线性方程→线性方程组→三变量线性方程组→方程组的不同解法.根据图式理论，人脑中有了概念、规则和策略的复杂的网络，而不是孤立的事实和算法，从而有利于帮助个人学到新知识.美国数学教育专家希伯特认为：人脑内部的知识联系是可以用对应的外部表示之间建立起的联系激发出来的[4].印尼2013版高中数学教科书每章的知识结构图很明显的目标就是希望用这样直观的联系结构图刺激学生头脑中的知识形成有效联系.

2.3 新教科书更加突出“问题解决”作为数学学习的抓手

印尼2006版数学教科书中每章最后都有一节来专门学习本章数学知识在实际社会生活、生产中的应用，突出“问题解决”为导向的数学知识的应用.几乎每章章末一节的标题均表达为“**在问题解决中的应用”.符合2013版数学大纲“学习与评估”中的要求：练习数学推理技巧，训练数学运算技能来解决问题;基于问题解决的学习.问题解决是建构主义教育思想和进步主义教育思想主张的重要观点，由这些教育思想主导的美国CCSSM数学教科书中有明显的“问题解决”为导向学习的特点.但是美国教科书中的问题解决是“时时刻刻”将知识融入在学习过程各个环节的“问题情境链”中，而不是像印尼2006版教科书这样的在每个知识点中专门设立一个问题解决的小节.印尼2013版高中数学教科书更具有美国教科书特点和风格，在印尼2013版高中数学课程大纲中这样表述学习目标：发展数学能力是为了提高生活技能，特别是在建立推理、交流和解决问题方面.2013版高中数学教科书开头就有这样的表述：

本书从提出问题开始，这些问题源于学生的事实和文化环境.学习目标是希望能够通过解决所提出的问题来发现数学概念和原理，并探索其中所包含的对于解决生活问题非常有用的属性.

印尼2013版教科书将数学知识尽可能融入各种问题情境中.例如在高一年级教科书第二章章首就有这样的学习目标：设计一个三变量情境问题的数学模型，解决数学模型以获得所给出问题的解决方案，解释解决问题的结果.其他章节也以数学问题或实际情景问题导入，通过解决问题学习数学、掌握数学知识性质.

2.4 新教科书能明确展示章节学习目标

不同于2006版教科书，2013版印尼数学教科书在每章章首均明确展示本章学习目标，让学生在学习之初就能明确知道自己在本章中需要了解哪些知识？知道哪些知识？掌握哪些知识？会应用哪些知识？例如在高二年级“积分”一章章首就有这样的学习目标：描述代数函数的不定积分，并且根据其导函数的性质分析积分的性质;解决与代数函数不定积分有关的问题;描述代数函数和的不定积分;通过使用函数导数的性质确定反函数导数性质.解决与不定积分代数函数有关的问题.

“凡事预则立，不预则废“，教育家布鲁纳以及美国伊利诺伊州中小学数学委员会均认为：向学生提前提示他们要学习的全部内容，有利于学生自我发现学习[5].

2.5 新教科书倡导在数学学习中的数学交流

印尼2013版教科书在开头的前言中有这样的表述：数学概念和原理的发现和理解是由您和您的朋友在学习小组的指导下进行的.努力独立学习、思考，提出问题、与别人讨论，与更了解问题的人（朋友）辩论.

例如在高一第三章中对数学建模结果的要求还包括：解释解决问题的结果.解释肯定包括解释给同学、老师听，这也是数学交流的一部分.诸如此类对数学交流的要求在印尼2013版教科书中较频繁出现.交流有利于增加学生对数学知识的理解程度，应该是为了响应在2013版数学大纲“学习和评估”中的要求：主动而自主的学习，正确、系统地使用概念和性质，理解胜于仅仅记住性质.强调学习者对数学知识的理解.

2.6 印尼教科书是努力实现不同模块内容混合的学习

从教科书内容可以看到，印尼教科书概率、统计、函数等数学模块的内容在同一问题解决过程中混合使用，目的很明显，就是想突破数学内容条块分割学习的问题，让学生感受到数学内容本身的整体性和原有的一体性特点.这种观念也是全球基础教育阶段数学教育改革的共同目标.

2.7 印尼新数学科书具有“直线型”教科书的特点

总体上看，印尼新、旧教科书中除了有少数数学主题内容呈现出螺旋式上升的知识安排方式外，绝大多数内容的安排有“直线型”教科书特点，例如印尼教科书中學习多项式时，既有中国初中就学习的多项式基本性质，也包括在此基础上应用多项式除法性质求方程的解这样的多项式除法的应用，微积分也是在一个年级一次性学完.有明显的一次性“吃干榨尽”同一知识点内容的“直线型”教科书特点.

2.8 新教科书未体现出重视信息技术在数学学习中的辅助应用

虽然印尼2013版《高中数学教学大纲》提出要求：数学能力的培养还强调技能并科学使用科技设备进行技能性计算和表达形象直观的图象和图形[2].但是从2013版高一到高三的数学教科书中并未发现明显的使用信息技术对数学学习辅助的内容.

2.9 新教科书增加了数学文化和数学史的内容

数学文化和数学史对数学学习的促进作用已经得到多方面研究的验证，数学文化和数学史的学习一方面有利于培养学生数学学习兴趣，另一方面，有利于学生通过学习数学知识的产生和发展历史加深对数学知识实质的理解，也了解了数学的应用范围和应用方式.近些年，各国中小学数学教科书中越来越重视数学文化和数学史的使用，印尼2013版也有这样的特点，虽然数量有限，但是已经突破了原有教科书在这方面的传统编写方式.例如高三第一章就有对欧几里得（Euclid）及其成果的介绍，同时介绍了他在几何方面的主要贡献.第二章介绍统计学家罗纳德·艾尔默·费舍尔对数理统计做出的贡献等.

2.10 印尼新教科书注重学生非智力因素的培养

印尼2013版《高中课程大纲》中提出：解决问题并通过符号、表格、图表或其他媒介来沟通各自想法，以澄清问题，培养积极的态度;重视逻辑思维的态度以及批判性、细心、坚忍不拔的决心、不轻易放弃解决问题的追求的信心的培养.教科书中对上述非智力因素的培养融入各个知识点的学习过程中.例如在每一个“问题”解决过程中设计不同梯度的“次问题”，并且设置专门的探究环节，引导学生逐步自我探究，得出结论，并写出自己的结论的想法.

2.11 印尼新、旧教科书对函数的学习缺乏集合论初步的基础

集合论初步不是印尼教科书中函数内容的学习前提，从印尼理科教科书内容看，印尼高中理科数学教科书中并沒有中国自上世纪80年代以来高中数学教科书中的一贯沿用内容：集合论基础.集合论初步知识是上世纪“新数运动”后遗留在大多数国家中学数学教科书中的内容之一，因为函数的学习中涉及定义域、值域以及复合函数的定义域的问题，从各国实践经验看，集合论初步知识作为函数学习基础有利于函数知识的深入理解，也有利于学生今后在高等数学知识的学习过程中与中学数学知识形成有效衔接.中国大陆自上世纪80年代初由人民教育出版社数学室编写出版的高中数学教科书中就在函数概念的学习前加入集合论初步知识的学习，这种模式在2002年版的新高中课程课程标准及其配套教科书中也沿用下来.

3 反思

3.1 印尼高中新数学教科书编写模式受西方教育思想影响明显

从印尼2013版高中新数学教科书内容和结构看，印尼新教科书受到建构主义、进步主义教育思想的影响，尤其是教科书中突出问题解决、数学交流等上述教育思想中的重要内容，皮亚杰、杜威等人主导的建构主义和进步主义思想在西方国家基础教育界已经形成主流，例如问题解决为导向的教科书编写模式，上述教育思想认为：一方面，“问题解决”数学学习方式有利于学生理解数学知识，另一方面也培养了学生未来应用数学解决自身面临的生活、生产、科技需求的能力.从中国大陆现行数学教科书编写模式看，中国上世纪末开始的基础教育课程改革也一定程度上受到上述教育思想的影响.

3.2 印尼高中新数学教科书内容有利于与大学数学内容之间形成良好的衔接和过度

中国大陆高校使用的大多数高等数学教科书中直接使用反三角函数、三角方程、复数的三角形式、参数方程、极坐标方程来学习微积分相关知识，是因为上世纪80年代开始使用直到2002年新课程改革这一阶段的旧教科书中上述内容均为必修内容，因此与大学数学之间形成较好的衔接和过度.但是，经过2002年开始的数学课程改革后，现行高中数学整体内容已经发生了很大的变化，上述内容已从必修模块中删除，而大学高等数学教科书中并没有补充学习上述内容，因此形成中学、大学数学内容之间的断档，因为大学数学课时安排紧凑，大学数学老师无暇顾及补充大学数学教科书中没有安排的上述内容.本应与中学数学课程改革配套进行而形成合适衔接的大学数学内容一直雷打不动，一直没有对教学大纲和教科书内容进行改革，导致了很多学生进入大学后数学学习的困局.印尼高中数学教科书除了没有学习上述内容中的极坐标方程外，其余内容均作了较为系统地学习，有利于后续大学数学的学习.

3.3 注重学生能力培养是包括印尼在内的各国数学教育的基本要求

不局限于知识的传授，着重培养学生未来生活、学习、工作的能力，是各国数学教育目标的基本要求，印尼也不例外.印尼2013版《高中数学课程大纲》提出：对数学能力的培养包含在每个教育阶段的学习过程中，各模块数学能力如下.

代数：应用包含绝对值的单变量线性方程、包含绝对值的三变量线性方程组、函数、数理逻辑、数学归纳法、双变量线性规划、矩阵、行列式来解决日常生活中的问题.

几何和测量：在几何变换、平面、立体几何的问题解决中使用矩阵.

统计和概率：运用总体、样本数据的描述性统计、计数规则等解决日常生活问题中的概率问题.

三角：利用三角函数的比较，将直角及相关角、恒等式、正弦余弦定理、三角函数运用到日常生活的问题解决中.

微积分：使用代数函数极限、导数和积分解决问题.

注重能力培养是着眼于学生的全面成长、终生学习和应对社会变革的综合能力培养，各个国家的各阶段教育都在向这个方面努力.

参考文献

[1] kementerian pendidikan dan kebudayaan jakarta. model silabus mata pelajaran sekolah menengah atas/madrasah aliyah/sekolah menengah kejuruan/madrasah aliyah kejuruan[M]. Kementerian Pendidikan dan Kebudayaan，2017.

[2] 范良火.英国、荷兰和印度尼西亚等国数学课程发展和改革的研究及分析[J].教育导刊，2016（08）：20-24.

[3] 印度尼西亚教育和文化部.高中数学课程大纲（2013）[S]，https：//kursus.kemdikbud.go.id/index.php/standar/.2020-1-12.

[4] D.A.格劳斯等著，陈昌平等译.数学教与学研究手册[M].上海：上海教育出版社，1999：134.

[5] 布鲁纳著，邵瑞珍译.教育过程[M].深圳：文化教育出版社，1982：39.

作者简介

王奋平（1971—），男，甘肃凉州人，汉族，教授 ，主要从事跨国文化数学教育研究.

Nuraeni Ratna Sar（1980—），印度尼西亚人，南京师范大学在读博士.