工程测量平面控制网平差的快速精度评定方法
范思思 简捷
1.成都风云传说科技有限公司 四川 成都 610041
2.四川英徕测绘技术有限公司 四川 成都 610031
1 概述
新版的工程测量类规范[1~5]很多新增了相对点位精度的限差要求,需要平差软件系统实现控制网任意2点间相对点位误差椭圆在长半轴E和短半轴F、纵坐标X和横坐标Y、边长的纵向和横向等方向上的成果输出,以便计算控制网特定的精度指标,如隧道洞内测量控制网横向贯通中误差的计算、桥轴线长度中误差的计算。相对点位误差椭圆各要素计算是平差与数据处理软件系统的重要基础功能模块。
通用的、统一的测量平差与数据处理软件系统,对统一技术标准、打破行业壁垒、推进内业外业一体化、提高工作效率、适应信息化发展都具有积极的意义。建立相对点位误差椭圆各要素计算模型,寻求适用于计算机编程的快速计算方法,对提升测量平差与数据处理软件系统的功能具有重要意义。
2 计算模型
控制网中任意一边坐标增量的矩阵表达为[6]:

若把间接平差的参数向量的协因数分解表达为:

则控制网中任意一边坐标增量的协因数阵,既相对点位协因数阵为:


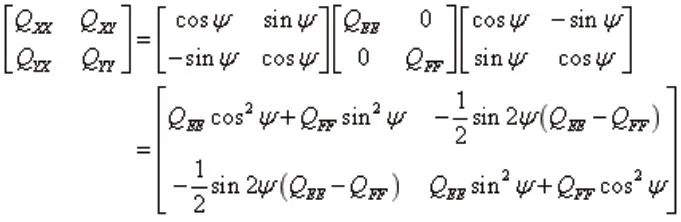
上图为平面测量控制网中的任意一边的相对误差椭圆,通过上述坐标系旋转变换方法,可建立坐标系、坐标系、坐标系间任意2 坐标系的转换关系,其中,转换后的协因数标量关系为:


图1 相对点位误差椭圆在3个特殊正交方向上的分量关系图
3 算例
算例来自误差理论与测量平差基础(第3版)[7],P145例[7-10]。

图2 平面控制网概图
根据本文的模型计算的输出成果表如下:

表1 相对点位及其精度成果表

表2 相对点位及其精度成果表
4 结束语
推导了基于坐标变换的快速相对点位误差椭圆在长半轴E和短半轴F、纵坐标X和横坐标Y、边长的纵向和横向等方向上的算法,在成果报表中可以直接获取所需参数的特殊方向的中误差,适应了新版工程测量规范对精度评定的需求。
——对2018年广州市一道中考题的研究

