一种基于属性加权的快速聚类算法∗

赵国伟 蔡江辉 杨海峰 荀亚玲

（太原科技大学计算机科学与技术学院 太原 030024）

1 引言

聚类分析［1～3］是数据挖掘中重要的无监督学习技术之一，与监督学习不同的是待处理的样本数据集中没有包含样本分类相关信息。聚类是把数据集中的对象划分成多个簇的过程，被广泛应用于市场研究、图像分割、网络安全及模式分类等众多新兴领域中。

K-means是一种经典的基于划分的聚类方法，由于其具有简单性和高效性被广泛运用于解决各种现实问题，例如文本分析、图像聚类、社区发现等［4］。此外，K-means采用距离作为相似性的评价指标，所以在处理数值型数据时能够更好地体现聚类在几何和统计上的意义。但是，常用的距离度量方法并没有对样本数据集各属性的内部结构以及其影响聚类划分的情况进行详细分析，即在对样本数据集进行划分时将数据所有属性的重要程度视为相同或者根据经验知识对属性的重要程度进行加权后再计算样本间的相似性。这样计算的距离并没有准确地反映数据间的相似性或因为经验知识不全面而产生误差，从而影响聚类的划分结果。针对传统K-means没有考虑属性重要程度的问题，本文提出了一种改进K-means算法，即FAWK。该算法定义了一个可以在领域知识未知的情况下区分数据属性重要程度的离散度函数，基于离散度函数提出了一种属性特征加权的距离度量方法，即AW（Attribute Weighting Distance）。在AW的基础上结合K-means算法思想提出了FAWK。

2 相关研究

经典K-means是一种简单有效的数据挖掘技术，其主要通过两个迭代步骤进行聚类：其一，根据目前数据划分情况来确定聚类中心；其二，根据划分标准对数据对象进行重新划分。

经典K-means常采用欧式距离作为数据划分的标准，然而欧式距离并没有考虑数据属性对聚类划分的影响程度，因此科学研究者们对属性的重要程度进行分析并提出了不同形式的相似度度量方法来衡量数据对象的相似性。文献［4］通过最大化子空间内各簇中心与其他簇的数据对象的加权距离提出了一种集成簇内和簇间距离的加权K-means（KICIC）。文 献［5］提 出 了 一 种 新 的L2-Norm正则化加权的K-means（l2WK）。该算法首先提出了一个子空间K-means聚类框架，然后对数据属性特征进行L2-Norm调整来排除部分噪音属性的影响，最后通过优化加权K-means的目标函数来判断算法是否收敛。文献［6］从数据对象的属性出发，通过属性偏离概率估量函数来确定数据属性的权重值并结合欧式距离提出了一种改进的加权欧式距离聚类算法（WEDK）。

以上算法在聚类过程中都侧重于数据属性的分析，却忽略了欧式距离本身的缺陷。因此，文献［7］针对函数型数据提出了一种新的基于导数信息距离的函数K-means（DIFK），实验结果证明了该算法的实用性和有效性。文献［8］提出了一种新的点对点距离度量的改进K-means（SK）。该方法定义了一个基于S散度的S距离（SD）来替换传统的欧式距离。实验结果显示该算法不仅适用于群集分布不规则数据还加快了聚类收敛速度。

选择合适的相似性度量对于揭示给定数据集中的自然分组是非常重要的，但是在对于K-means而言，初始中心的随机选择也将直接影响聚类结果的好坏。针对这一问题，文献［9］提出了一种空间密度相似性度量的K-means（SSMK）。该算法将可伸缩空间密度的相似性作为聚类划分标准，并结合密度和距离来选择初始聚类中心。此外该算法还构造了一种基于空间密度相似性的簇中心迭代模型来克服均值簇中心的缺陷。文献［10］根据簇类中心密度较高且方差较小的特点来干预初始聚类中心的选择，提出了一种最小方差优化初始聚类中心的K-means（MDK）。文献［11］提出了一种基于加权局部方差的密度计算方法，并利用改进的最大最小法启发式地选择初始中心点（WLVK）。实验结果证明该算法提高了聚类的效果，但是该算法具有较高的时间和空间复杂度。

此外，针对K-means根据经验值设置K的问题，文献［12］结合聚合距离参数和戴维森堡丁指数（DBI）提出了基于聚合距离参数的改进K-means（IADCK）；文献［13］提出了一种基于加权密度的最大最小距离的改进K-means（KWDM），该算法定义了准则函数来确定聚类的最优簇数K。虽然实验结果证明了IADCK和KWDM算法的有效性，但在初始聚类中心的选择和K值的确定过程带来了大量的时间开销。

3 算法思想

3.1 AW（Attribute Weighting Distance）

数据对象的信息主要存储在其属性上，因此数据的属性在数据挖掘中对数据的知识发现有不可替代的作用。然而不同的属性对知识的发现影响程度不同，尤其在K-means中，数据属性对聚类划分过程的影响更为明显。本文提出的AW是一种根据数据属性对聚类划分的影响程度不同来进行数据对象间相似度度量的方法。

在统计学常用平均值和标准差评价一组数值型数据的集中趋势和分散程度。然而多数真实数据集的不同属性在取值范围和取值单位上不相同，这时标准差不适合比较两组或多组不同尺度和不同量纲数据的离散程度。因此本文定义了离散度函数来解决这一问题，它可以在领域知识未知的情况下区分数据属性的重要程度。

定义1设数据集为二元组＜D，X>，其中D=｛di|i=1，2，3，…，n｝为记录集，di为单个数据对象；X=｛xij|j=1，2，3，…，m｝为属性集，xij为单个数据对象的属性特征，xij表示数据对象di的第j维属性特征，则数据集＜D，X>中的第j维属性的均值与标准差如式（1）、式（2）所示：

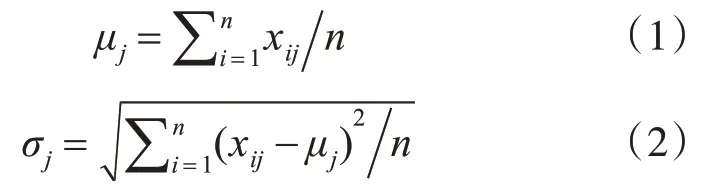
定义2离散度函数（Discrete Function，DF）表示属性的离散程度如式（3）所示：

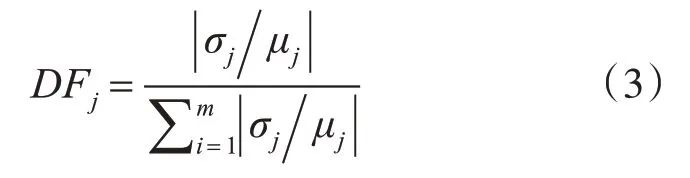
其中，如果μj=0且σj≠0，则|σj/μj|=σj；如果μj=0且σj=0，则DFj=0；DFj∈［0，1］。数据属性的DF值越大表示该属性值的集合的分布越离散，则该属性对聚类的划分过程影响程度越大，反之越小。DFj=0表示数据集＜D，X＞中的第j个属性离散程度为0，即在聚类过程中第j个属性可以忽略不计，此时可将其删除来降低算法的时间和空间开销。

基于各属性的离散程度，计算数据属性间的相似度如式（4）所示。样本间的相似度为各属性间的距离求和所得，其表达式如式（5）所示。

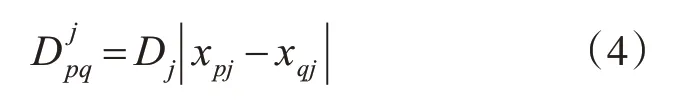
在式（4）和（5）中，p∈｛1，2，…，n｝、q∈｛1，2，…，n｝且p≠q。Djpq表示样本p和样本q第j维属性的相似度，AWpq表示样本p和样本q的相似度距离，其中xpj和xqj分别表示样本p和样本q的第j维属性。

3.2 FAWK算法描述

基于传统K-means的基本原理，结合3.1节提出的相似度度量方法，本文提出了FAWK算法。该算法的基本思想是先根据式（3）计算每维数据属性特征的DF值，然后随机选择K个样本点作为初始聚类中心，并根据式（5）进行初次数据划分；根据划分结果更新聚类中心，并对划分结果进行分析判断，检测是否达到迭代截止条件；反复执行，直到算法满足迭代截止条件时聚类完成。

3.3 时间复杂度分析

K-means算法的时间复杂度为O（lKnm），其中l为算法的迭代次数，K为簇的数目，n是所有对象的数目，m是对象所包含的属性的数目。FAWK的时间开销主要有两部分组成，其一是数据属性离散程度计算带来的时间消耗，该部分的时间复杂度为O（nm）；其二是聚类划分过程的时间开销，这部分的时间复杂度为O（lKnm）。因此，整个算法的时间复杂度为O（lKnm）。本文所涉及的几种聚类算法的时间复杂度汇总表如表1所示。

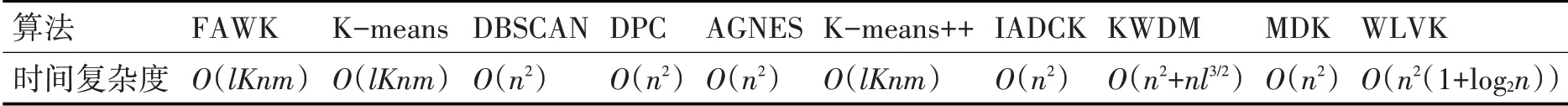
表1 算法时间复杂度汇总表

4 实验结果与分析

为验证FAWK算法的有效性，本文首先将FAWK在不同的UCI数据集上进行实验，并与传统K-means［14］、K-means++［14］、DPC［15］、DBSCAN［16］、AGNES［17］、IADCK［12］、KWDM［13］、MDK［10］和WLVK［11］共9个不同的聚类算法进行实验对比分析。其次，将本文提出的AW方法与欧式距离（ED）、加权欧式距离（WED）、夹角余弦距离（ACD）、切比雪夫距离（CD）和SD［8］五种用于聚类算法的相似度度量方法进实验测试与分析。最后，以LAMOST项目作为应用背景进行算法验证。

4.1 UCI数据集实验分析

本文选取了UCI数据库中的8个标准数据集作为实验测试数据。8个数据集的相关信息汇总表如表2所示。

对于任何一种算法的验证都需要对其进行合理的综合评价，基于不同的算法，会有不同的评价方法或评价指标。本文用基于聚类结果的准确率（AC）对实验结果进行评价。AC指的是聚类结果中预测正确的样本占总样本的比。各聚类算法在不同数据集上独立实验的聚类结果准确率统计如图1所示。

图2展示了基于不同相似度度量方法的K-means在8个UCI标准数据集上独立实验的聚类结果准确率。结合图1和图2，可以发现FAWK的大部分实验结果优于其他几种聚类算法，仅有少部分实验结果不是最优，但其也并不是最差的，因此图1和图2的实验结果证明了本文所提算法的有效性。

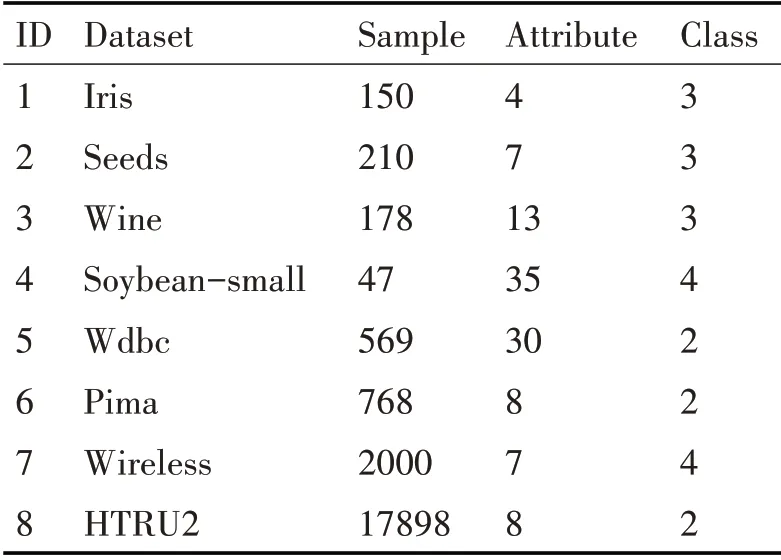
表2 实验中使用的数据集信息汇总表

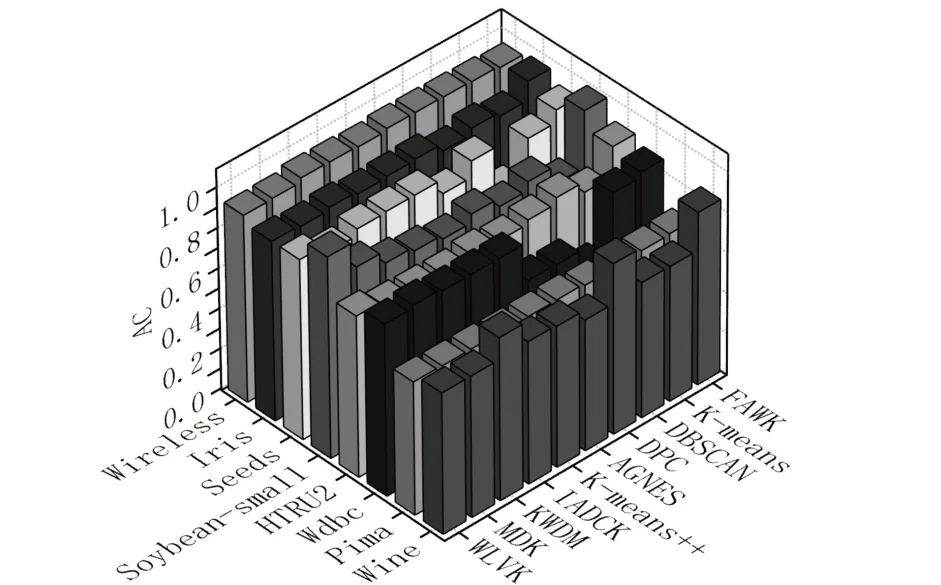
图1 10个聚类算法在不同数据集上的准确率统计图

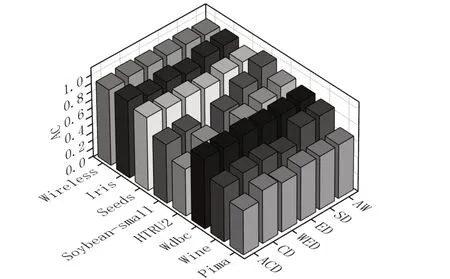
图2 基于不同相似度度量方法的K-means算法的准确率统计图

图3分别统计了各算法在不同的数据集上独立运行十次的平均时间消耗情况。图3中的子图（a）展示了各算法对六个数据量相差较小且总量相对较小的数据进行聚类实验的平均运行时间；子图（b）和子图（c）展示了各算法在两个数据量相对较大的数据集HTRU2和Wireless上实验测试的平均运行时间。分析图3可以发现FAWK运行时间与其他几种算法相比较快，尤其在Pima、Wireless和HTRU2数据集上本文算法的运行时间与其他算法对比优势更加明显。

图4统计了基于不同相似度度量方法的K-means在8个标准数据集上独立运行十次的平均迭代次数。图4显示，本文所提方法的平均迭代次数少于其他几种相似度计算方法，说明本文所提方法能很好地反映数据间的相似度，减少了算法的迭代次数，加快了聚类的收敛速度。结合图4和图2可以发现将加权欧式距离作为K-means算法聚类过程的划分标准对Soybean-small数据集进行实验测试的平均迭代次数为2，聚类结果的准确率为36.17%，由此可知该聚类过程陷入了局部最优。

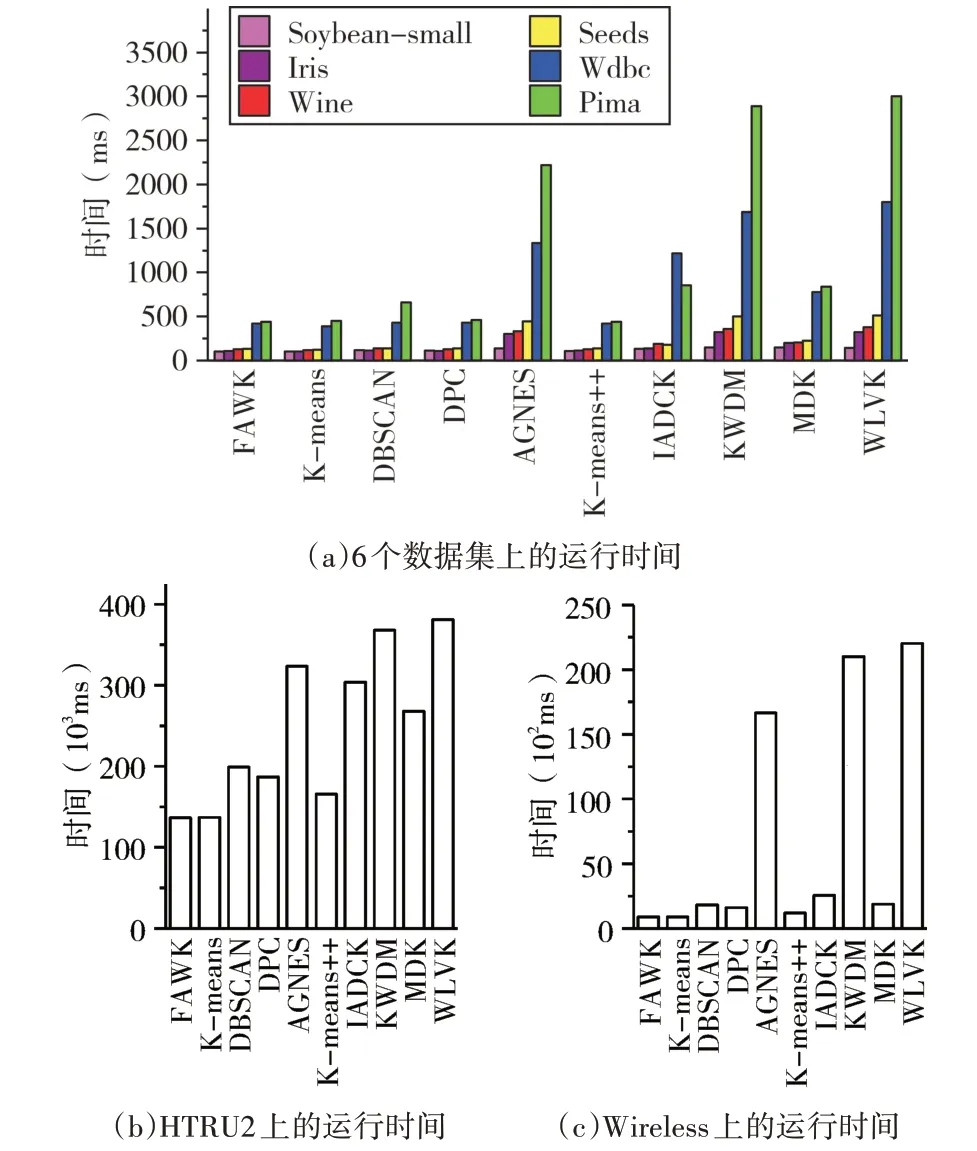
图3 各算法在不同UCI数据集上的运行时间统计图

4.2 恒星光谱数据实验分析

为了验证本文所提出聚类方法的实用性，从LAMOST DR5［18～19］中随机选取SNR大于等于40的A、F和G类恒星光谱数据组成光谱数据集进行实验测试与分析。由于原始数据的Flux都超过3000维且不是标准数据，所以在进行实验前先使用最大最小方法［20］对光谱数据进行归一化，并根据哈佛分类系统的恒星分类依据以及恒星天体光谱研究领域专家的经验和意见，选定恒星中普遍存在的28个元素的吸收线周围最近邻的三维Flux数据来构造数据总量为1000、2000、5000、10000和50000共五个不同量级吸收线特征集进行聚类实验分析。

图5为光谱数据集的聚类结果准确率统计图，图中垂直于纵坐标的实线为辅助线。从图5中可以发现在不同量级的光谱数据集上FAWK聚类结果的AC保持相对稳定且优于其他几种算法，说明其具有一定的实用性。

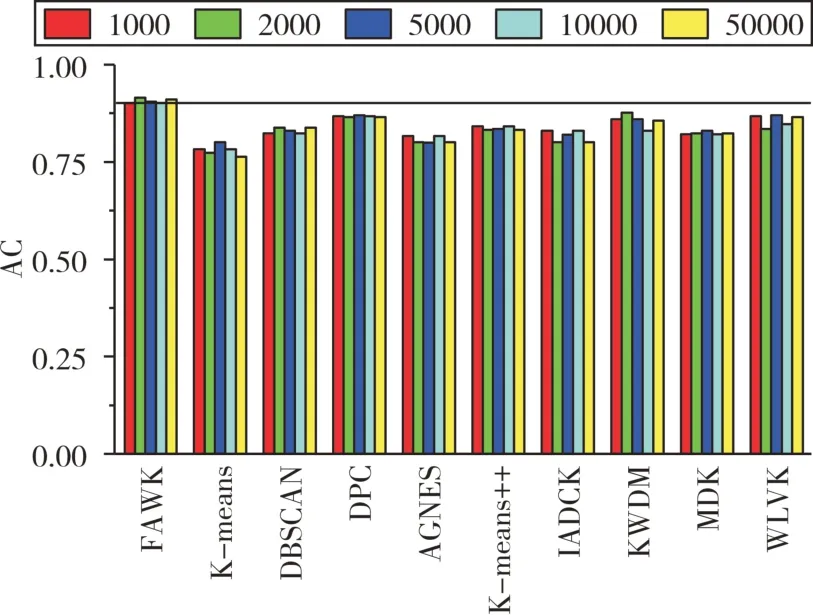
图5 恒星光谱数据的聚类结果统计图

图6展示了各算法在不同量级的恒星光谱数据集上独立运行十次的平均时间消耗情况。图6中横坐标为不同量级的光谱数据集，纵坐标为平均运行时间。图6中子图为矩形框中折线的局部放大图。

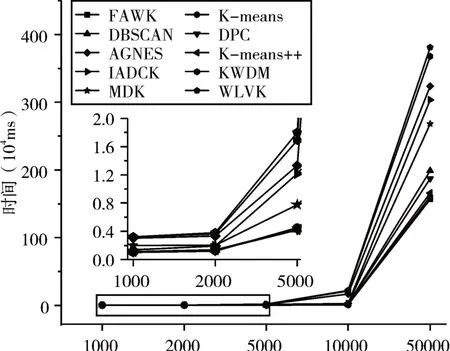
图6 各算法在恒星光谱数据集上的运行时间

分析图6可以发现FAWK在光谱数据集上的平均运行时间与K-means相接近且优于其他几种聚类算法，随着数据量的增加本文算法的运行时间与其他算法对比优势明显增加。由3.3小节可知本文算法的时间开销相比传统K-means增加了第一部分数据属性离散程度计算带来的时间消耗，但是结合图3和图6可以发现FAWK与传统K-means的平均运行时间近似相等，出现这种情况的原因主要有两方面：其一，传统K-means采用欧式距离来度量样本间的相似性，本文所提算法采用加权属性求和作为样本间的相似度度量方法，而本文算法在计算样本间相似度时的时间开销要小于计算欧式距离所带来的时间开销；其二，本文所提的AW方法减少了算法的迭代次数，加快了聚类过程的收敛速度。因此，FAWK虽然在离散程度计算过程增加了一定的时间开销，但是其整体算法的运行时间与传统K-means的运行时间相接近且低于其他几种聚类算法。

5 结语

聚类是一种重要的无监督学习方法，它以数据为基础通过学习数据中的信息来实现分组，而属性特征是构成数据样本的基本单元，是数据信息最原始的载体，不同的属性在取值范围、分布情况和重要程度上存在一定的差异。为解决聚类样本的各属性对聚类结果影响程度存在差异的问题，本文融合K-means提出一种基于属性加权的快速K-means算法。该算法通过离散度函数来分析和量化不同数据属性的重要程度；然后结合各属性的重要程度定义了新的相似度计算方法作为K-means算法的聚类划分标准。在UCI和LAMOST数据集上的实验结果证明了本文算法的有效性和实用性。此外，本文提出的AW是一种度量数据样本间相似性的计算方法，接下来将进一步对其扩展研究以适用于不同的聚类算法。