基于小波去噪法的南水北调工程沉降预警
孙 飞,翟福雷,方 琪
(1.南水北调东线江苏水源有限责任公司宿迁分公司,江苏 宿迁 223800;2.中科宁图技术江苏有限公司,江苏 南京 211100)
南水北调东线工程是解决我国北方地区水资源严重短缺问题的重大战略举措,从长江下游取水,沿京杭运河向北送水,至山东、河北、天津,以解决京沪沿线和山东半岛城市缺水问题,并为农业和生态补水。泗洪站枢纽工程是南水北调东线工程的第四梯级泵站,设计流量为120m3/s,其主要任务是将第三梯级抽入洪泽湖的江水通过运西线徐洪河继续北送至第五梯级濉宁站,再由房亭河入骆马湖。枢纽位于江苏省泗洪县朱湖乡东南的徐洪河上,三岔河大桥下游4km、洪泽湖顾勒河口上游约16km处。该枢纽是南水北调的重要节点,自建成运行以来一直在进行安全监测,积累了较多数据,所以,对其安全监测成果进行研究很有必要。文章采用小波去噪法对安全监测数据进行处理,剔除测量误差,然后根据去噪后的数据进行沉降预警与分析,指导枢纽的运行与维护。
1 安全监测数据

泵站工程自2013年以来,底板位置沉降9mm左右,最大累计沉降位移量为-13mm;上左翼沉降2mm左右,最大累计沉降位移量为-7.1mm;上右翼沉降7mm左右,最大累计沉降位移量为-10.8mm;下右翼沉降6mm左右,最大累计沉降位移量为-8.7mm;下左翼沉降1mm左右,最大累计沉降位移量为-7.7mm,其中2014年9—12月,发生了上升回弹现象,2016年汛后较汛前沉降明显,12月较9月又发生了数据回弹现象,从检测数据来看,汛期沉降在2~7mm波动。部分观测数据见表1—2。

表1 泵站2013—2015年部分垂直位移监测数据 单位:mm
2 小波去噪
2.1 小波去噪理论
在实际工程建设中,传统的去噪方法是利用一个滤波器除掉带有噪声污染的信号中的噪声相应的频率波段,具有很强烈的局限性。小波分析去噪作为全新的克服信号缺陷的一种分析方法,已经成功地广泛应用于多个领域。小波就是一族小波基函,描述了信号空间和尺度的局部特性,小波的局部分析是其最大优势,可在任意的时间域或空间域中进行信号分析。
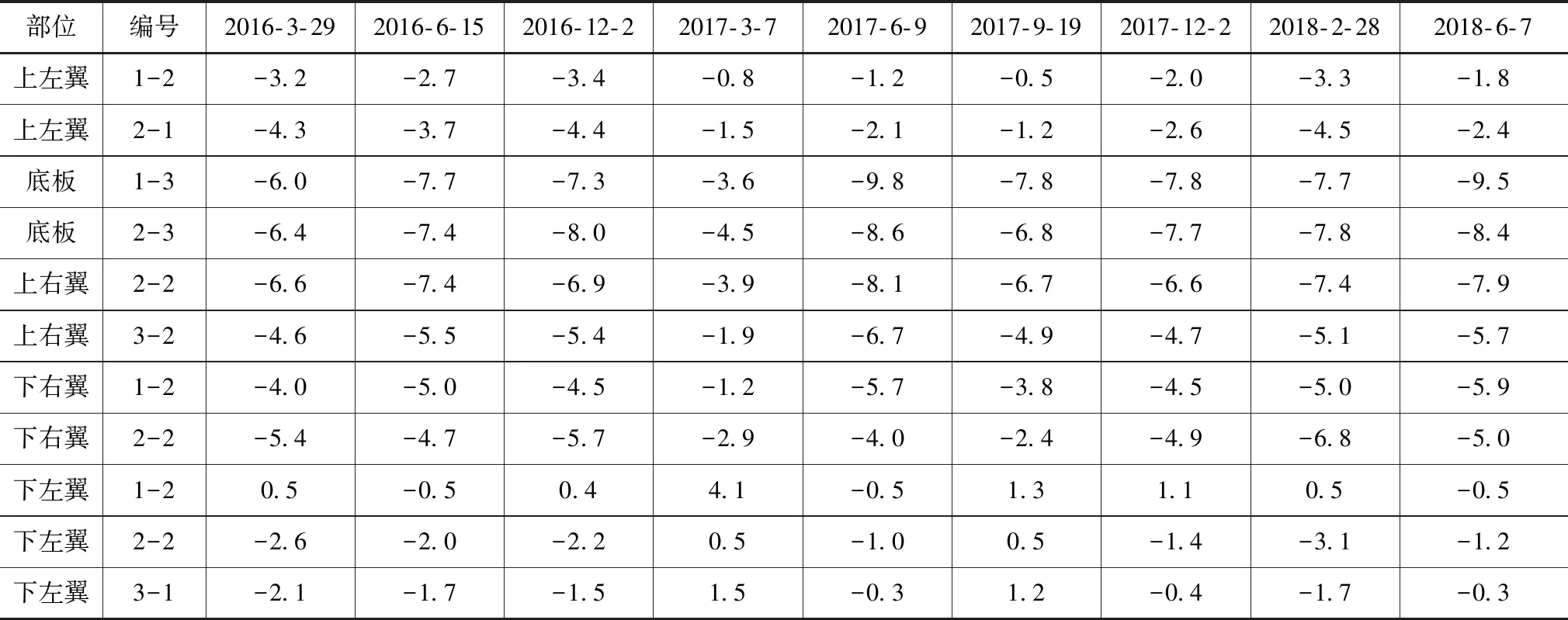
表2 泵站2016—2018年部分垂直位移监测数据 单位:mm
小波分析方法在图像处理和数据去噪中有着广泛应用,常见的小波去噪方法有小波分解与重构法、小波阈值去噪法、平移不变量法和小波变换模极大值法,其中阈值去噪方法实现简单、计算速度快,具有广泛的适应性,是众多小波去噪方法中应用最为广泛的一种[1]。阈值去噪方法是通过小波对信号进行分解得到各层系数,然后构造相应的阈值,对大于或小于阈值的系数分别处理,将处理后的小波系数进行重构达到去噪的目的[2]。其去噪原理如图1所示。其中,S表示原始信号,A表示近似信号,D为噪声部分,下标为分解的层数。

图1 小波去噪原理图
泗洪站垂直位移监测数据都是离散序列,所以采用离散小波变换(DWT)。在数据序列的时频特性上,噪声信号的分布是全局的,对小波系数的各个尺度都有影响,目标信号的分布是局部的,主要特征集中在比较大的小波系数上,因此只要用合适的阈值对小波系数进行处理,剔除噪声产生的小波系数,同时保留有用信号的小波系数,就可以去除数据中的噪声。小波去噪的流程图如图2所示。

图2 小波去噪过程图
常用的阈值去噪函数有软阈值去噪法和硬阈值去噪法。硬阈值去噪法是当小波系数的绝对值小于给定阈值时,令其为零;大于阈值时,令其保持不变,即
(1)
软阈值去噪法是当小波系数的绝对值小于给定阈值时,令其为零;大于阈值时,令其都减去阈值,即
(2)
文章主要采用db4小波函数将其分成3层进行分解,然后确定阈值标准进行小波重构,从而去除误差噪声。
2.2 小波去噪过程
由于测量时间并不固定,测量间隔有长有短,因此为了消除时间序列的不平稳趋势,需要对测量数据进行两次差分运算,消除其趋势性。然后利用标准化处理公式,对数据进行标准化处理,从而得到预处理的数据。通过计算自相关和偏相关系数,来检验预处理后的数据是否符合AR建模要求。
根据偏相关函数截尾性,初步判断模型阶次为5。用最小二乘法估计参数,计算10阶以内的模型残差方差和AIC值,应用AIC准则为模型定阶。求得的所有AIC值分别为172.6632,165.4660,153.2087,145.1442,140.7898,141.6824,142.9944,144.5601,146.3067,148.7036。
取使AIC值为最小值的阶次,从而判断模型阶次为5。检验数据是否为白噪声,求该数据的自相关系数,看其是否趋近于零,若自相关系数接近于零,则数据可看作是白噪声,应予以去除。
以底板的2-3测点为例,去噪后的数据与原始数据对比如图3所示。

图3 去噪前后数据对比
3 沉降预测与分析
3.1 回归分析沉降预测方法
在进行预测分析方面,回归分析法适用于单点分析情况。该方法基于对变形观测数据和影响因子进行回归分析以及逐步回归计算分析,由此得到变形与影响因子的函数关系式,回归分析需要定性地分析变量之间的相关关系,当自变量与因变量存在某种关系时,建立的多元回归模型才有实际预测的意义。
在建立线性回归方程后,需要对回归方程进行统计检验,即根据因变量与自变量之间是否具有相关关系进行显著性统计假设检验。预测模型的检验一般有F显著检验、T显著检验、拟合优度的检验和回归标准差检验等方法。只有当他们间存在线性关系,回归方程才具有实际意义。
文章主要以泗洪站的监测数据为依据进行沉降分析,考虑到温度和荷载对闸站沉降的影响,选取4期同月份数据,时间间隔为1年,建立多元线性回归预测模型,预测泗洪站沉降曲线。
3.2 回归分析沉降差异分析与预警
3.2.1垂直位移特征值计算
安全预警的第一步是需要对垂直位移特征值进行计算,它是预警模型中的一个参数,所以文章针对泗洪站垂直位移监测数据进行特征值计算。均方差作为数据离散程度的衡量指标,3δ准则又被称为拉依达准则,它是先假设一组检测数据只含有随机误差,对其进行计算处理得到标准偏差,按一定概率确定一个区间,认为凡超过这个区间的误差,就不属于随机误差而是粗大误差[6]。特征值的计算就是根据已有的监测数据进行统计计算,所以将均方差和3δ准则考虑其中,以2δ作为垂直位移的预警特征值,特征值的计算公式如下:
(3)
式中,λ—垂直位移特征值;xi—每个测点的监测值;r—平均值。
其中底板、上右翼、上左翼、下右翼均值及特征值曲线如图4—7所示。

图4 底板均值及特征值曲线
3.2.2垂直位移预警
对于水工建筑物之一的泵站而言,某测点在t时刻的垂直位移主要是由沉降相关量、温度、时间效应这3种因素的共同作用引起的,其通用数学模型为
δ(t)=δH(t)+δT(t)+δθ(t)
(4)
式中,δ(t)—垂直位移效应量在时间t的统计估计值;δH(t)—沉降相关量;δT(t)—温度位移;δθ(t)—时效位移。

图5 上右翼均值及特征值曲线

图6 上左翼均值及特征值曲线

图7 下右翼均值及特征值曲线
选取泵站底板等水工建筑物结构连同复合地基为研究对象,对其进行单元网格划分,并将泵站垂直位移测点的位置作为单元节点之一,根据泵站及基础的结构形式给定相应部位的物理力学参数。
根据若干个特征值λ1,λ2,λ3,…,λn计算得出相应的沉降相关量值,利用有限元法分别计算在不同沉降相关量作用下测点的垂直位移量δ1,δ2,…,δn。由这些位移计算值采用回归分析建立沉降相关量H(t)与垂直位移δi(t)的关系,得到一元多项式:
(5)
式中,αi—回归系数;n值一般取3或4。
考虑到时效位移δθ(t)是一种随时间推移而逐渐增长的变形,一般与时间呈曲线关系,由于成因较复杂,故利用数理统计方法得出其关系式:
(6)
式中,c0,c1,c2,c3,c4—由统计分析确定的系数;t—位移观测日相对基准观测日的日序值乘以1/365。
根据泗洪站垂直位移的日常监测资料,建立垂直位移混合模型。由前面的垂直位移模型构造式,将水压因子的拟合式作为一个单独的待选因子;温度因子以观测日前j天到前k天的日平均气温Tj-k作为温度影响的待选因子,具体采用前1~10d,前11~30d,前31~60d,前61~90d,前91~120d共5个待选因子;时效因子以ln(t+1)、1-e-t和t等3个因子作为时效影响的待选因子[9],则泗洪站垂直位移的混合模型表达式为

(7)
取显著性水平为0.01,引入因子、剔除因子的F统计量限值为2.50,由此建立各个测点垂直位移的混合模型,代入上式得出混合模型公式:

(8)
所建的位移混合模型的复相关系数在0.96附近,剩余标准差为0.72mm,剩余标准差S占实测变幅的4.8%,小于10%,且对实际位移情况拟合较好。
根据以上原理,建立垂直位移监控预警值的公式:
[δm]+=ΔδHmax+ΔδTmax+δθ+δ0
(9)
[δm]-=ΔδHmin+ΔδTmin+δθ+δ0
(10)
式中,ΔδHmax,ΔδHmin—最高、最低闸前沉降量与初始闸前沉降量的差值;ΔδTmax,ΔδTmin—极值温降/升日与初始温度分量的差值;δθ—初始日至监测序列最后一天的时效分量;δ0—初始日垂直位移实测值[10]。
由此,沉降相关分量、温度分量和时效分量的极值可根据水平位移混合模型各部分的分离结果分别计算得出,代入式(10)可拟定出泗洪站垂直位移安全监控预警值,截取2015—2017年底板向上、向下垂直位移监控预警值,详见表3。

表3 底板垂直位移监控预警值表 单位:mm
3.3 回归分析预测精度与结果
回归分析法作为预测模型最基本的预测方法,且有一个好的预测效果,所以文章将基于小波去噪的对数函数沉降预测模型应用于泗洪站,并输出三条曲线:原始数据折线、去噪后数据折线、去噪后拟合曲线。将三条线段进行对比,可以直观判断出预测曲线与原有数据的拟合度。预测过程中的残差平方和与拟合优度的求解过程如下:
(1)计算残差平方和及相关系数R2(拟合优度)。
(2)计算平滑后的数据的总和zh。
(3)计算平滑后的数据的平均数pjs。
(4)根据模型公式求每一点的预测理论值。yc[i]=ratio3[0] *(Math.Log(x[i]))+ratio3[1],其中ratio3为拟合数据,yc为预测理论值数组,x为时间。
(5)计算每一点的残差值。cc[i]=rec[i]-yc[i],rec为平滑后的数据,cc为残差数组。
(6)根据公式计算残差平方和ccpfh。ccpfh=Math.Pow(cc[i],2),并保留四位小数。
(7)计算观测值与平均数之差的绝对误差,并求总平方和zpfh。
(8)根据公式计算相关系数R2,公式为xgxs=1-ccpfh / zpfh。
经过上述处理最终得到如图8所示的沉降预测图。

图8 泗洪站沉降预测曲线图
图8中两条折线分别表示泗洪泵站原始垂直位移底板1-4监测数据和经过小波去噪后的折线,然后文章根据小波去噪后的折线重采样数据对其使用对数函数进行拟合,生成图中平滑曲线,其中自2018年6月7日起进行预测,预测结果生成的报表如图9所示。
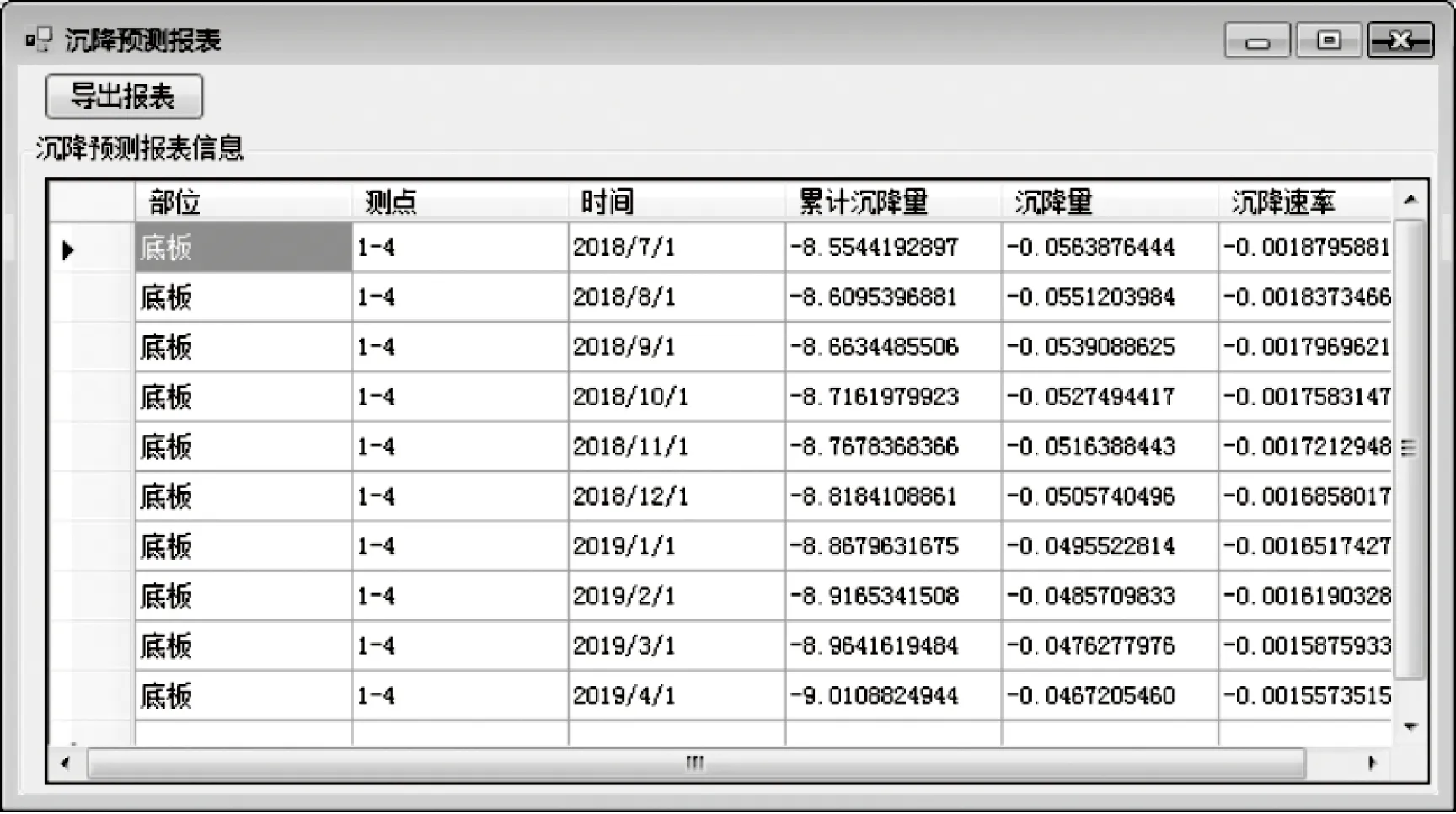
图9 泗洪站沉降预测报表
4 结 语
文章从基于小波去噪的对数函数入手,将泗洪站沉降预测与模型相结合,通过分析,使用该方法进行预测具有一个较好的效果。同时对垂直位移的特征值进行了计算,分析出差异沉降量,将其作为影响因子运用于预警模型中,计算得出不同时间的预警值。文章也存在一些不足:
(1)实验数据量不足且数据在时间上应尽量满足每期的时间间隔大致相同,文章运用的时间间隔后期较大,对模型影响较大。
(2)设计的预测不够全面,只适合该测区,换其他监测数据所建立的预测模型不是很理想。
(3)文章提出的预警模型虽求出预警值,满足实际情况,但没有进行可靠性验证,今后应从多个方面综合分析以得到更理想且更加符合实际的闸站预测预警模型。

