对《建筑与市政工程地下水控制技术规范》的几点商榷
尚许雯,尚银生
(1.山西省交通规划勘察设计院有限公司,山西 太原 030032;2.山西省勘察设计研究院有限公司,山西 太原 030013)
2017年3月实施的JGJ 111—2016《建筑与市政工程地下水控制技术规范》[1],将原规范[2]适用范围降水工程扩展为地下水控制工程,增加了隔水帷幕、回灌、监测的设计和施工相关规定,对有关内容进行了大量的合并、修改、补充和完善;明确了强制性条文“地下水控制工程不得恶化地下水水质,导致水质产生类别上的变化”。但其中个别基本概念、有关地下水渗流的部分计算公式仍有待商榷。
1 关于钻孔注水试验渗透系数计算时利用的形状系数
JGJ 111—2016推荐的钻孔常水头注水试验的渗透系数计算式为
(1)
式中,K—土的渗透系数,cm/s;Q—稳定水流量,cm3/ s;F—形状系数,cm;H—试验水头,cm。
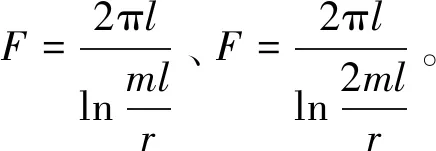
显然,JGJ 111—2016附录A简图示意的水文地质概念模型都属于半无限厚含水层中的非完整井,含水层很厚,从而近似地忽略了隔水底板对水流的影响,因而在实际工程应用中存在一定的局限性;否则,还应考虑隔水底板的影响,将含水层作为有限厚来处理。
即便以半无限厚含水层来处理,根据渗流理论,以井底进水、井底与井壁同时进水的承压水非完整井为例,其流量计算公式相应为[3-6]:
Q=2πKrs
(2)
(3)
式中,r—井半径,cm;s—水位降深,cm;其他符号意义同上。

同样都是以达西定律为基础,假定含水层半无限厚等推导而来,但井底进水时两者形状系数差别较大;井壁进水时两者比较接近。因此,有必要探寻问题的根源及更为恰当的渗透系数计算公式。
无论是井底进水的潜水、承压水含水层,还是井底、井壁同时进水的潜水、承压水含水层,它们都是半径为r的钻孔,形状相同,进水条件相同,似乎形状系数应该相同但却不同。因为它实际上包含了众多试验条件。即利用同样的公式[式(1)],只是用不同的形状系数,来反映不同的水力性质——潜水或承压水;来反映不同的进水条件——井底进水、井底与井壁同时进水;来反映半无限厚含水层渗流特征,显然有些简单化。何况,虽然称之为形状系数,但量纲却是长度,或者说,以长度量纲反映形状至少还不够确切。因此,形状系数不是一个恰当的术语。SL 345—2007《水利水电工程注水试验规程》对其定义为反映钻孔注水试验段边界条件的参数,其中明显包含了水文地质信息。或许,直接根据地下水动力学渗流理论及水文地质试验、数值模拟的利用,能够得到更为适宜的、相应水文地质条件下的渗透系数计算公式。
2 关于井壁允许出水能力及单井出水能力
(1)JGJ 111—2016中5.3.7节规定管井过滤器长度宜与含水层厚度一致。当含水层较厚时,过滤器的长度可按下式计算确定:
q=π·d·ne·v·l
(4)

该式利用的滤水管进水流速是吉哈尔特经验公式,进而计算单井出水量,而吉哈尔特经验公式是根据含水层岩性特征,来计算井壁进水流速,并以此来确定单井出水能力。因此,式(4)不仅将(设计)单井出水量与单井出水能力、也将滤水管进水流速与井壁允许进水流速混淆在一起。
(2) 附录C.0.5中降水管井的单井出水能力按下式确定:
(5)
式中,r—过滤器半径,m;k—土的渗透系数,m/d。
实践教学是增强高校思想政治教育实效性的必要环节,闽东特色文化资源为高校实践育人提供了丰富的物质和精神素材。[8]把闽东特色文化资源融入实践教学的主要方式有:
3 非完整井向完整井的转化条件
JGJ 111—2016中条文解释4.2.3节中提到:对于巨厚含水层,水位降深与含水层厚度相比较小时,可转化为完整井计算。
在含水层很厚或埋藏较深的地区,由于受经济技术条件限制或因含水层部分厚度就能满足工程的要求,常采用非完整井开采地下水,或降低地下水水位。按过滤器在含水层中的进水部位不同,非完整井分为井底进水、井壁进水、井壁和井底进水三类。地下水流向非完整井的水流形式与完整井的水流形式不同,流向非完整井的地下水流为三维流,而且,当其他条件相同时,非完整井的流量小于完整井的流量。再者,水量计算时必须考虑过滤器在含水层中的位置和顶底板对水流状态的影响,如果含水层很厚,则可以近似地忽略隔水底板对水流的影响,按半无限厚含水层来考虑,以半无限厚含水层中的非完整井、井壁进水的潜水非完整井为例,
(6)
当水位降深与含水层厚度相比较小时,它依然是一个不完整井井流计算公式,因为在这个井壁进水的潜水非完整井公式中,由于含水层很厚,利用的是过滤器长度,未涉及含水层厚度。
当水位降深与过滤器长度相比较小时,上式可简化为
(7)
式中,R—影响半径。
4 关于非稳定流状态下的影响半径
JGJ 111—2016中4.4.4条提出:降水影响半径的确定可按下式计算:
(8)
非稳定流理论中,无论是Theis公式还是Jacob公式,本身不包含影响半径的概念,因此,理论上讲,在无限延伸的无越流补给的含水层中是不存在影响半径的。
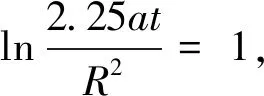
将用于承压水计算的Jacob简化式(式9)与稳定流理论Dupuit公式(式10)作对比,即

(9)
(10)
将用于潜水水量计算的Jacob简化式(式11)与稳定流理论Dupuit公式(式12)作对比,即
(11)
(12)
都可得出上述结论。然而对于非稳定流理论,无论是Theis公式还是Jacob公式等,都可以直接计算任何位置、任何时间的降深,因而再计算所谓的影响半径无任何意义。如JGJ 111—2016中式(E.0.1-1)、式(E.0.1-3)虽然没有影响半径这个参数,但已经进行了有关水位的预测。
5 其他
(1)JGJ 111—2016中2.2节符号中,T为导压系数,应为导水系数,而且似乎没有必要在此列出,因为JGJ 111—2016中并没有直接利用该系数。
(2)式(C.0.3-1)、式(C.0.3-2)中常用对数应为自然对数。
(3)条文解释4.5.1节、4.5.2节中L3应为L4。

(5)式(E.0.2-1)、式(E.0.2-2)与表B.0.5中线状基坑涌水量计算公式本质相同,只不过前者根据水流连续性原理利用已知一个断面的位置与水头等来计算所求断面的水位降深。因此,附录E.0.2“条状……”应该为“线状……”。
6 结论
由于地下水控制工程的复杂性及人工地基对水文地质条件的改变,需要相应的理论公式或经验公式来尽可能正确地反映地下水渗流特征[8],简单化的形状系数难以响应。当有利用三维流理论解决问题的条件时,尽可能不利用平面二维流理论;当有利用非稳定流理论解决问题时,尽可能不利用稳定流理论,并尽可能利用数值法。因而JGJ 111—2016应包括相应鼓励性研究型条款。

