居住区共享停车场运营策略
关宏志, 聂楚濠, 赵鹏飞
(北京工业大学城市建设学部, 交通工程北京市重点实验室, 北京 100124)
随着城市内的机动车保有量与使用率不断增加,停车难已经成为城市不容忽视的问题[1-3]。为此,人们展开了多方面的研究和实践活动。在诸多缓解停车难措施选项当中,如何提高现有停车资源利用率成为人们关注的焦点。张新洁等[4-5]通过优化停车收费定价,提高车位利用率以缓解停车难的问题。当前,共享经济模式成为一种新的发展方式,一方面能够降低商品的闲置率,另一方面消费者仅需用较少的成本便可享受商品服务而不必购买所有权[6]。在此背景下,共享停车(shared parking)也成为在充分利用现有资源解决部分地区停车问题的一个重要选项[7-8]。所谓共享停车,是指由于不同类型的停车用户对某一停车场产生的停车需求在时间上并不相同,如居住区业主,即车位提供者(O-users)在白天离开居住区时,自己的私家车位处于空闲状态,而此时附近的社会停车用户(P-users)需要停车。若能开放私家车位的使用权,则可在不额外新建车位的情况下,进一步满足部分停车需求,减少寻找车位的时间,也能使得O-users在一定程度上获益。正是由于共享停车解决方案具有不需要过多的城市资源的特点,引起了许多人的兴趣。
当前,关于共享停车的研究主要为共享停车资源配置以及共享停车收益问题。其中一部分学者从提高泊位资源利用率以及提高管理者收益的角度入手研究共享停车问题。Shao等[1]通过考虑拒绝停车请求的惩罚和严格的时间窗约束,提出一种基于预约模式的车位统一分配模型;张雷等[9]构建向量自回归预测模型及泊位共享分配双层模型,研究了城市中心区共享停车的可行性、停车预测方法及共享泊位分配策略问题;张文会等[10]则从考虑用户效益的角度出发,提出解决多个共享停车场车位分配问题模型。姚恩建等[11]以泊位资源最大化利用为目标,构建共享车位资源配置模型并设计相应的求解算法;孙会君等[12]则是综合考虑租用车位成本,接受请求获取利益与拒绝用户请求与拒绝租用车位可能造成的潜在损失,提出以运营商利润最大化为目标的整数规划模型;Guo等[13]以仿真优化的方法确定泊位的回购策略,以利润最大化为目标,决策最优车位回购数量和共享停车运营平台的最佳运营时间;郭放等[14]构建了适用于车位共享短时动态需求预测的向量自回归(VAR)模型,在最小共享时长为1.5 h的约束下,确定各时段可开放的车位数量和时间窗动态调控策略。也有学者从共享停车各个参与者的角度入手,研究共享停车问题。段满珍[15]将博弈论引入共享停车理论,从分析驾驶人、车位拥有者、管理者的偏好入手,结合居住区共享停车的需求,构建了基于APP共享停车管理框架下的居住区共享停车服务模型;在此基础上还构建了居住区停车位对外共享服务能力评估模型[16],用于描述居住区参与共享停车的服务能力;李新新[17]则建立了两方参与、三方参与以及三方选择性合作等收益分配模型,并研究了泊位拥有者特性、不同合作模式等因素对管理者总收益的影响。李涛等[18]考虑停车用户冲突的问题,研究在避免冲突的情况下,如何最大化管理者总收益的问题。Zhao等[19]构建了一种共享停车资源管理框架,在该框架下开发了一个智能停车管理系统处理停车用户冲突的问题。实行共享停车时一方面要求P-users必须严格守时,在O-users返回前驶离车位,另一方面亦要求O-users在共享时段内不在居住区内停车。但在实施共享停车时,O-users可能由于某些不确定的原因而在共享时段内返回居住区停车,而此时自己的车位正在被使用,从而造成O-users返回时无车位可停的问题,即O-users与P-users在停车时间上冲突的问题。该问题如果不能得到妥善解决,可能导致共享停车失败。因此,如何解决O-users与P-users在停车时间上冲突的问题就成了共享停车政策得以很好应用的关键。然而,上述研究并没有很好地解决这些问题,其通常是考虑在共享停车实行前预留一定比例的车位供提前返回业主停放,并未考虑到如何在共享停车开始实行过程中根据O-users返回居住区停车的规律设置保留车位,以满足提前返回居住区的业主停车的需求来解决用户冲突问题。
针对这些问题,提出在实施共享停车中动态保留一定数量车位,满足O-users停车需求进而缓解用户冲突的想法,以居住区共享停车为对象,对共享停车运营策略中的如何设置保留车位数量以及如何确定变更共享策略时间的问题进行研究。
1 问题描述及模型建立
假设存在一个服务于某居住小区的停车场,车位总数为N,与车位拥有者的数量相同,即每一位业主都拥有自己的私家车位,车位仅允许业主即O-users使用。O-users在白天离开居住区外出时,车位处于闲置状态,而居住区附近在工作时间存在着大量的停车需求。
现将小区内所有的私家车位在白天某一时段的使用权由某一企业统一租赁并进行运营管理。管理者允许O-users可在任一停车位停车,只是不确保在某一特定的车位,以此保证停车场的车位依然可以满足O-users的停车需求,同时也能更好地实施停车共享。
针对O-users与P-users在停车时间上冲突的问题,考虑了“拒绝用户冲突”和“允许用户冲突”两大场景,针对这两个场景下的多个模式进行情景分析。
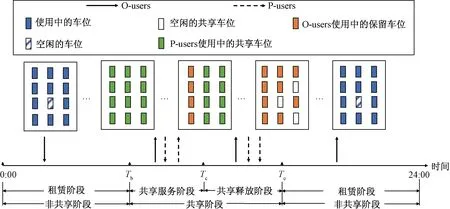
图1 居住区共享停车场一天的演化规律Fig.1 The evolution of shared parking spaces in residential areas within a day
假设停车场在一天内的演化规律如图1所示。假设该居住区的停车场管理者租用O-users的私家车位每车位每天的价格为PR元/(车位·h),管理者将车位出租给P-users每车位单位时间的收费价格为PS元/(车位·d)。假设O-users在某一时刻(该时刻设为Tb)全部离去,即开始实施停车共享的时刻,然后O-users会按一定规律返回居住区。假设停车需求足够大,只要共享入口开放,非保留车位就会一直处于饱和状态。但是由于O-users陆续返回,所以管理者需要在P-users驶离停车场后保留一定数量的车位供O-users停放。为此,管理者需要在某位P-user离开后将该车位保留起来,以不断增加保留车位的数量,从而保障陆续返回的O-users有车位可停。但是保留车位的增加速率上限是P-users离开停车场的速率上限VPout/辆/h。从某一时刻开始(该时刻设为变更共享策略的时刻Tc),O-users将陆续全部返回居住区,此时必须控制共享入口的进场,此后P-users可以其最大速率VPout离去,直至某一时刻(该时刻设为共享阶段终止时刻Te)全部离场,共享结束。其中Tb至Tc时段为共享服务阶段,Tc至Te时段为共享释放阶段,这两个阶段合称为共享阶段。其余时段为管理者租赁O-users的私家车位的租赁阶段,即非共享阶段。
O-users的返回规律对停车场运营方案的制订至关重要,不同情况下的O-users的返回规律并不相同,为了研究在不同情况下的最优运营方案,假设O-users的返回规律大致分为以下两种情况。
规律一:在Tb至某一时刻Ti(该时刻设为O-users开始集中返回的时刻)时段内,O-users以恒定速率VOin1辆/h返回居住区;在Ti至Te时段内,O-users以恒定速率VOin2辆/h返回居住区。当停车场的车位数量N足够大,而单位时间返回的O-users数量比较多的时候,其微小的波动可以忽略不计。基本属于这种情况。

针对以上两种O-users的返回规律,需要确定合适的变更共享策略的时间Tc以控制进入居住区停车,确保P-users能够在共享时段结束后全部驶离停车场。在此背景下,研究如何控制保留车位数量,在满足O-users和P-users的停车需求的同时,使得管理者收益最大的问题,基于线性规划理论,建立优化模型并提出求解算法。
1.1 拒绝用户冲突场景下的运营策略分析
若不允许O-users与P-users发生停车冲突,此时需要停车场的空余车位必须始终大于或等于返回的O-users数量,这仅能在O-users以固定速率返回居住区的假设下实现。下面对O-users以固定速率返回居住区的情况进行分析。
1.1.1 P-users离开速率小于O-users集中返回速率时的策略分析
假设居住区共享停车实施开始后,O-users 将分别以VOin1速率零星返回居住区,至Ti时刻则开始以VOin2速率集中返回,其速率均为固定值。P-users将在Tc时刻开始被管理者禁止其驶入居住区停车,同时以其最大驶离速率VPout离开居住区,以此保证至Te时刻全部驶离居住区。
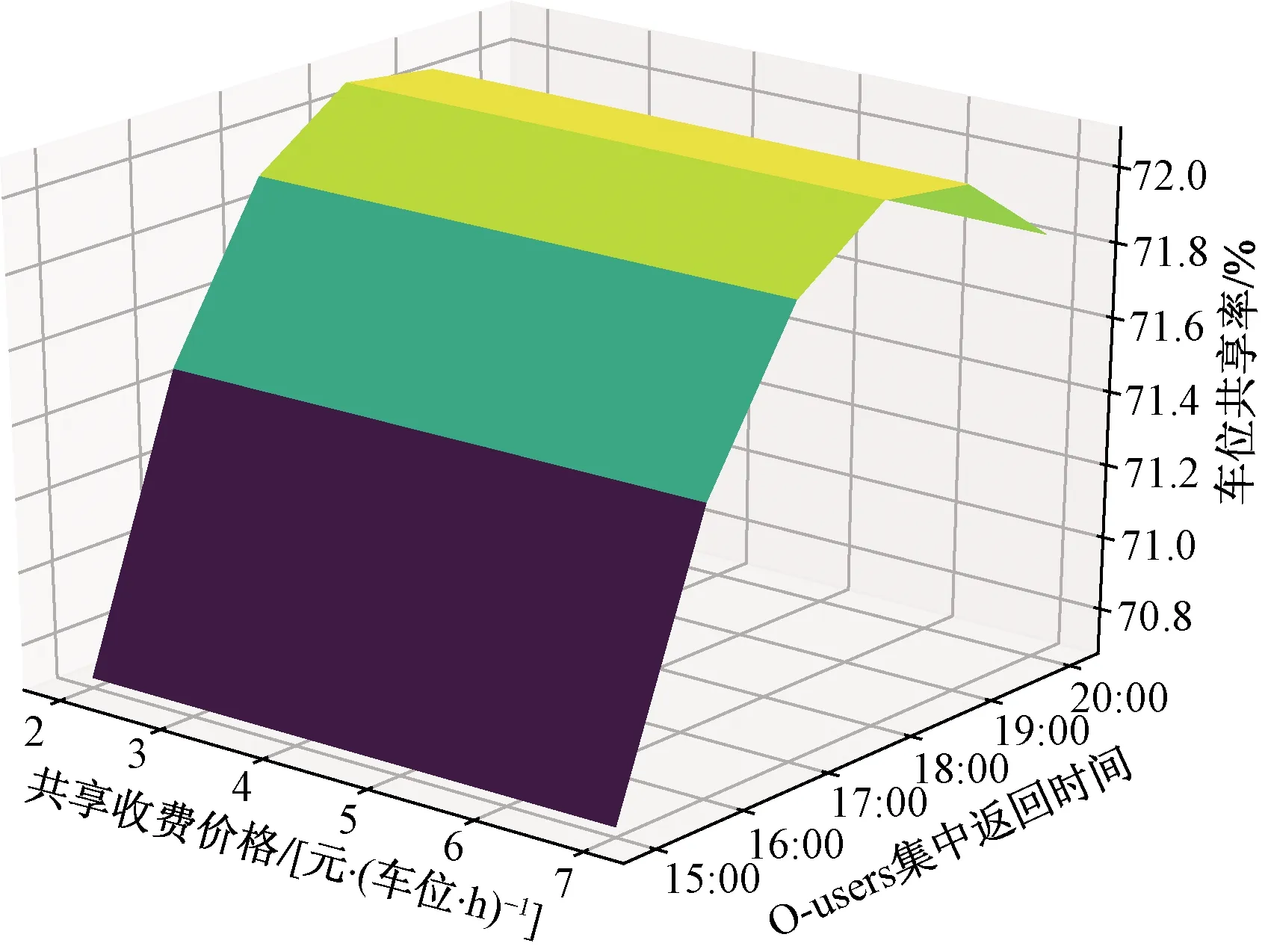
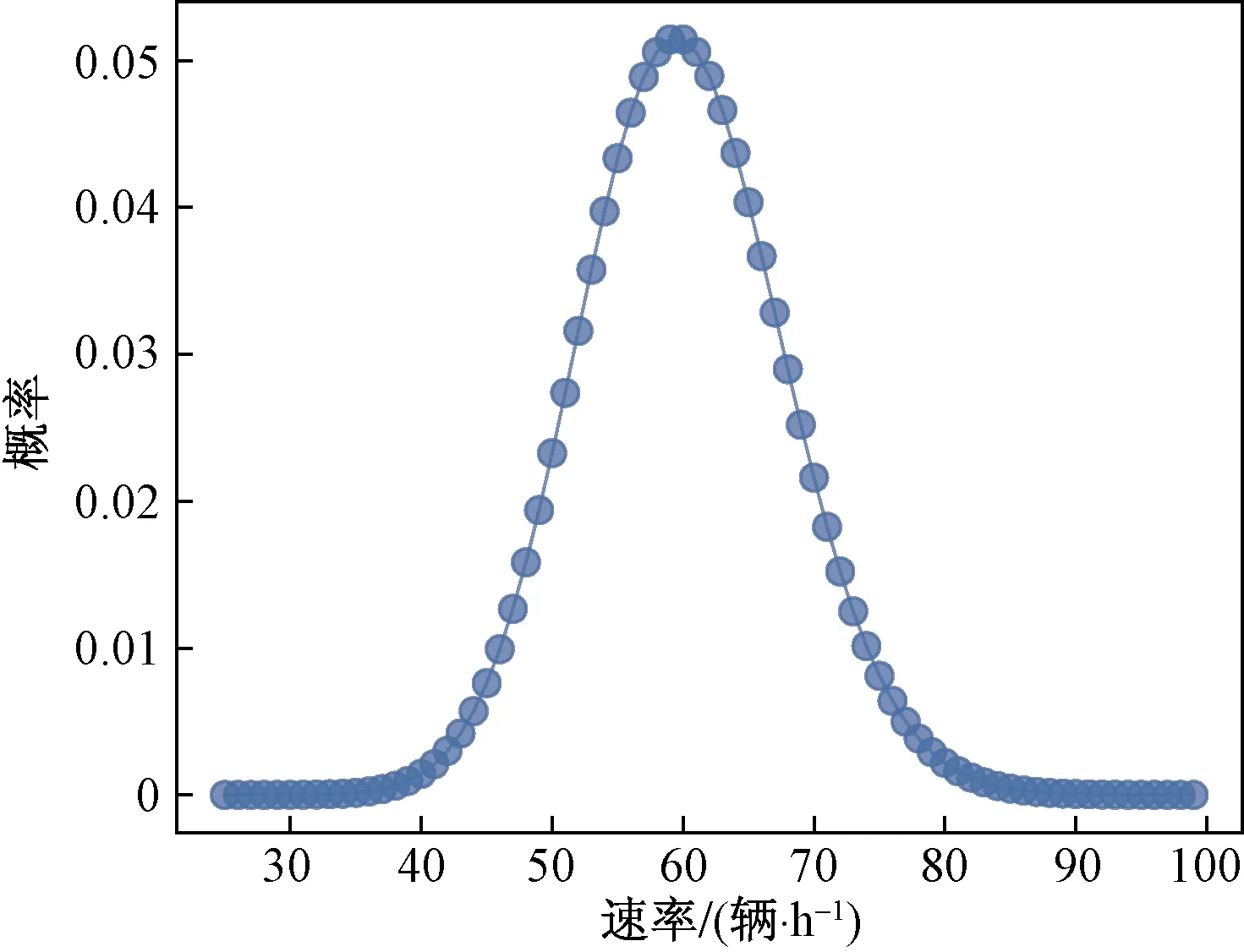
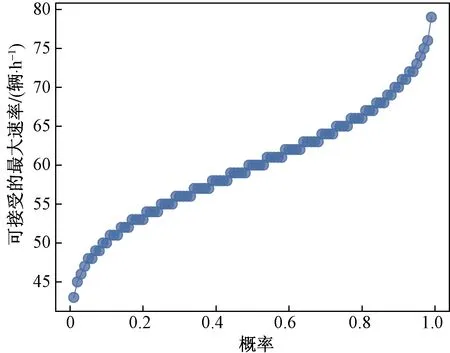
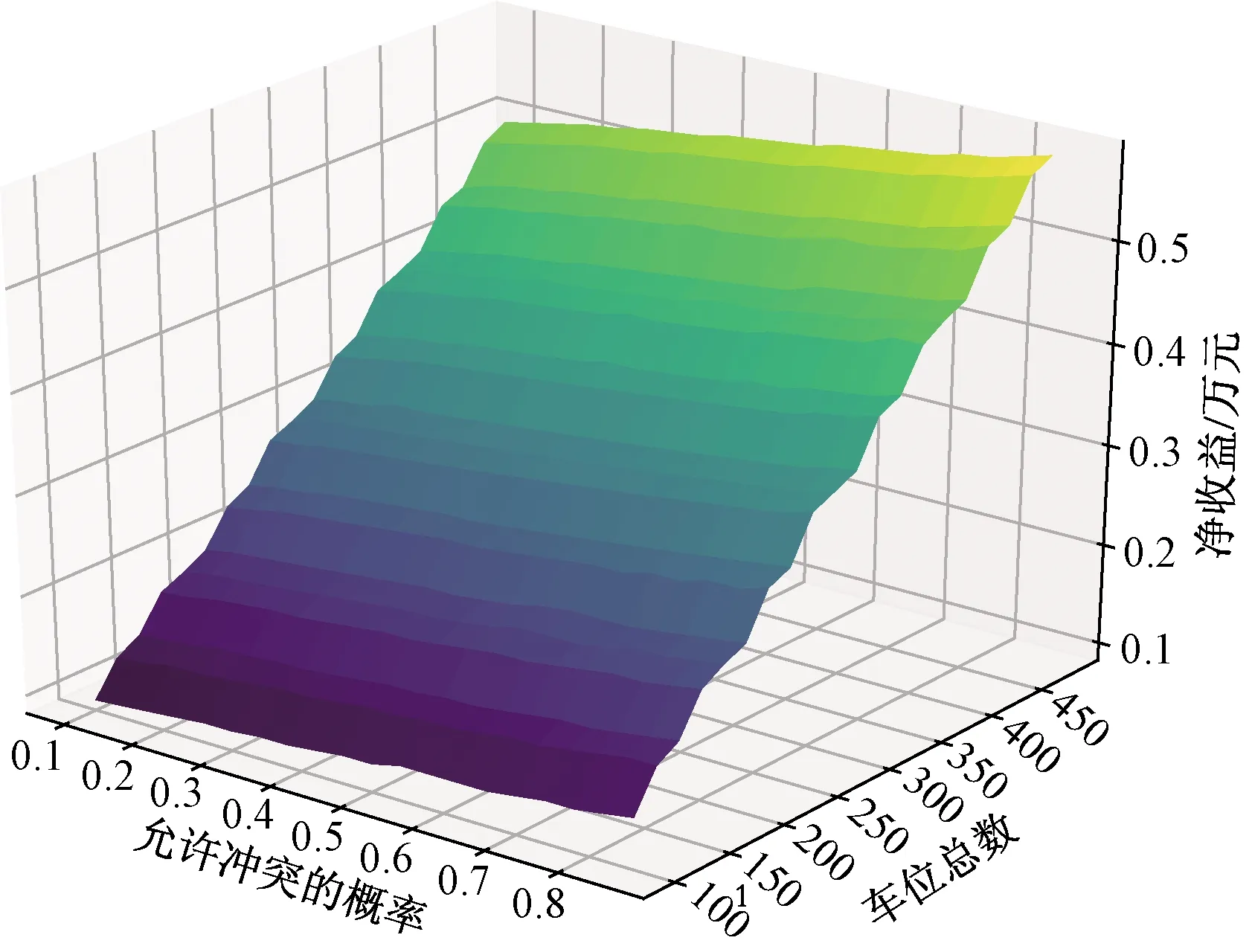
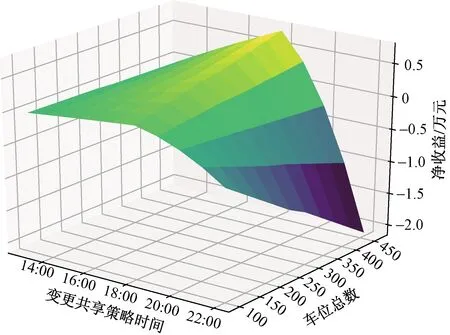
当VPout 图2 停车场车位随时间变化Fig.2 The number of parking spaces in the parking lot changes over time 由图2可知,O-users于Tb时刻全部驶离居住区停车场并于该时刻开始实施共享停车,此时O-users开始以VOin1的速率零星返回,并于Ti时刻开始以VOin2的速率集中返回居住区。由于假设的两个返回速率均为固定值,因此返回的O-users的数量呈分段线性增加的趋势,直至Te时刻所有的O-users返回居住区,达到居住区业主数量的最大值N。为此,居住区停车场的保留泊位在P-users全速离开时(即变更共享策略的时间Tc)前需要控制其增长率与返回的O-users速率相同,故在Tc前保留泊位数量线性增加且与O-users数量相同。而在此之后,由于P-users以最大速率VPout离开,保留泊位的数量线性增加至共享阶段结束时刻Te达到最大值N。设在t时刻,O-users的数量为fO(t),由图1可得到其关于时间的函数为 (1) 设在t时刻,共享车位的数量为fshare(t),故其关于时间函数可表示为 (2) 由于O-users一定会在Te时刻全部返回居住区,则 fO(Te)=N (3) 由式(1)、式(2)及式(3)可解得Te为 (4) 又因在Tc时刻,保留车位数量刚好与O-users的数量相同,即 N-fshare(Tc)=fO(Tc) (5) 则变更共享策略的时间Tc为 (6) 停车场的车位共享率ρ定义为实际共享的车位数时长与最大可共享车位数时长的比值,即 (7) 设管理者的共享收益为Γshare,租赁车位所花费的成本为Γbuy,所求得目标函数为管理者的净收益,简称净收益Γall,则 (8) Γbuy=NPR (9) Γall=Γshare-Γbuy (10) 1.1.2 P-users离开速率大于或等于O-users集中返回速率时的策略分析 当VPout≥VOin2时,为确保管理者的收益最大,仅需在O-users集中返回的时刻Ti处限制P-users进入停车场即可,此时应使得Tc=Ti。由于O-users的返回速率较小,在变更共享策略时刻Tc之前,可控制保留车位增长率等于O-users返回速率VOin1,而在Tc之后,仅需控制保留车位增长速率与O-users返回速率VOin2相等,居住区停车场车位随时间变化如图3所示。 图3 停车场车位随时间变化Fig.3 The number of parking spaces in the parking lot changes over time 从图3中可以看出,返回居住区的O-users数量始终等于保留车位的数量,因为当P-users的离开速率VPout大于或等于O-users的集中返回速率VOin2,那么在变更共享策略的时时间Tc无需完全关闭共享入口亦可使得O-users不与P-users发生停车冲突。此时仅需控制保留车位的数量与返回O-users数量相等即可。根据上述约束关系可得 Tc=Ti (11) 因此,共享终止时刻Te为 (12) 共享车位关于时间的函数可表示为 (13) 停车场的车位共享率为 (14) 管理者的净收益表示为 (15) 假设允许一定概率下的O-users与P-users发生停车冲突,因为这种策略下管理者可以利用更多的车位进行共享,并以此增加盈利。但是当O-users返回居住区没有车位时,也存在其终止合作从而使共享模式难以为继的情况,所以有两种允许冲突的情况:一是车位总数N很大,少数车主停止合作不影响整个系统的运行,那么可以根据经验定出一个允许冲突的最大概率p0,这种模式设为接受固定概率的冲突模式。另一种是假如管理者不能承受业主终止合作的影响,那么此时管理者可以采取提供补贴的方式来解决这一问题,即当O-users返回没有车位时,管理者提供资金使O-users于邻近的停车场停泊,这种模式设为补贴模式。如果附近没有车场,管理者甚至可以安排工作人员帮助其停到稍远的停车场,待本车场有位置时再调度回来,不过这样做的成本较高,通常为共享收费价格的数倍,记补贴费用为Pp元/(车位·h)。 1.2.1 O-users返回速率为固定值时的策略分析 O-users为固定速率返回时不存在冲突概率的问题,仅存在用户一定冲突与用户一定不冲突两种情况。而当VPout≥VOin2时,管理者总可以控制保留车位数量与返回的O-users的数量期望值相等,此时不存在因冲突造成的惩罚费用,因此这种情况的分析则与固定速率下VPout≥VOin2相同。所以下面仅分析VPout 由于O-users在前期返回速率较低,仅需保留少量车位即可满足返回的O-users的停车需求,因此在前期不必接受冲突,所以假设前期的保留车位增加速率和O-users的返回速率相同,从Tc时刻开始,P-users 被禁止进入停车场,转而全速驶离,显然应该有Tc≤Ti,否则将出现较多的停车需求无法得到满足,甚至导致用于补贴的费用超过停车收费总额,运营方将可能面临亏损,停车场车位随时间变化如图4所示。 图4 停车场车位随时间变化Fig.4 The number of parking spaces in the parking lot changes over time 由上述约束可求得共享阶段终止时刻Te为 (16) 设在t时刻保留车位的数量为fhold(t),可由下式计算 (17) 返回的O-users的数量函数表示为 (18) 设未被满足的停车需求数量为fmiss(t),其用函数表示为 fmiss(t)=max[fO(t)-fhold(t),0] (19) 管理者租赁车位的成本为 Γbuy=NPR (20) 因此,共享车位的净收益为 (21) 设因未满足O-users需求产生的成本为Γmiss,则 (22) 则管理者净收益为 Γall=Γshare-Γbuy-Γmiss (23) 1.2.2 O-users返回速率服从泊松分布的策略分析 根据上文假设条件,若采取补贴的方式处理用户冲突的问题,那么计算的方式与O-users的返回速率为固定值的情况类似,因为当O-users的返回速率服从泊松分布时,仅能分析其期望,从而根据期望进行决策,而泊松分布的期望是等于固定速率的。 若是给定可接受的冲突概率p0的情况,概率p0会影响O-users集中返回的最大速率VOin2,此时可通过累计概率密度函数计算出最大冲突概率为p0时的可接受的最大速率值,之后可参照固定速率的情况进行分析。 表1所示为模型设计的参数定义及其在数值实验中的默认初始值,在此基础上,逐步对相关的参数进行敏感性分析。 根据表1所示条件,绘制出P-users的离开速率和车位总数对管理者净收益、共享阶段终止时刻以及车位共享率的影响,如图5~图7所示,其中, P-users离开速率是指其单位时间内离开车辆数占车位总数的比例,共享停车的净收益以万元为单位表示。 表1 参数定义 图5 净收益随P-users离开速率与车位总数变化Fig.5 The net income changes with the P-users’ departure rate and the total number of parking spaces 图6 车位共享率随P-users离开速率与车位总数变化Fig.6 The parking sharing rate changes with the P-users’ departure rate and the total number of parking spaces 由图5~图7可知,随着P-users离开速率的增加,当P-users的离开速率小于O-users集中返回速率时,管理者运营停车场的净收益与车位共享率都随之逐渐提升,同时变更共享策略时间随之延后;而当其与O-users集中返回速率近乎相同时,管理者的净收益与车位共享率达到最大,而变更共享策略时间开始稳定在一个值,随后净收益、车位共享率以及变更共享策略时间均不再变化。随着车位总数增加,净收益随之增加,而车位共享率和变更共享策略时间基本不变。 图8~图10展示了O-users集中返回时间和共享收费价格对净收益、变更共享策略时间以及车位共享率的影响。 图7 变更共享策略时间随P-users离开速率与车位总数变化Fig.7 Change of sharing policy time with P-users’ departure rate and the total number of parking spaces 图8 净收益随O-users集中返回时间与共享收费价格变化Fig.8 The net income changes with the O-users’ gather return time and shared charge price 图9 车位共享率随O-users集中返回时间与 共享收费价格变化Fig.9 The pariking sharing rate changes with the O-users’ gather return time and shared charge price 图10 变更共享策略时间随O-users集中返回时间与共享 收费价格变化Fig.10 Change of sharing policy time with the O-users’ gather return time and shared charge price 由图8~图10可知,随着O-users集中返回时间的延后,管理者的净收益有所提升,因为停车场将会有更多的车位可利用时间供P-users使用,车位共享率先增后减,在18:00—19:00的时候达到最大,同时变更共享策略的时间也随之延后。随着共享收费价格的提升,管理者的净收益随之提升,而车位共享率和变更共享策略时间保持不变。 2.2.1 接受固定概率的冲突模式 假设O-users返回速率均值为60辆/h,其泊松分布概率密度曲线如图11所示,允许的冲突概率与可接受的最大速率关系如图12所示。 图11 参数为60的泊松分布概率密度曲线Fig.11 Poisson distribution probability density curve with parameter 60 图12 参数为60的泊松分布概率与最大速率映射曲线Fig.12 The poisson distribution probability with parameter 60 and the maximum rate mapping curve 允许的冲突概率、车位总数对管理者的净收益、变更共享策略时间、车位共享率的影响如图13~图15所示。 图13 净收益随允许冲突的概率和车位总数变化Fig.13 The net income changes with the probability of allowable conflicts and the total number of parking spaces 图14 共享率随允许冲突的概率和车位总数变化Fig.14 The sharing rate changes with the probability of allowable conflicts and the total number of parking spaces 由图13~图15可知,随着允许冲突的概率增加,管理者便可拿出更多的车位可利用时间用于共享,其净收益也增加,但增加幅度较小,同时变更共享策略时间延后,而车位共享率基本保持不变。而随着车位总数的增加,管理者净收益随之增加,同时变更共享策略时间有微小提前,但是共享率震荡增加。 2.2.2 补贴模式 变更共享策略时间、车位总数对管理者的净收益和车位共享率的影响如图16、图17所示。 图16 净收益随变更共享策略时间和车位总数变化Fig.16 The net income changes with change of sharing policy time and the total number of parking spaces 图17 车位共享率随变更共享策略时间和车位总数变化Fig.17 The sharing rate changes with change of sharing policy time and the total number of parking spaces 由图16、图17可知,随着变更共享策略时间的延后,管理者的净收益和车位共享率均呈现先缓慢上升,在18:00附近达到最大值,随后快速下降的特点。随着车位总数增加,当变更共享策略的时间在18:00前时,净收益也增加,当其在18:00后时,净收益随之减少,而车位共享率先缓慢减少,在车位数为250附近有显著提升,然后继续缓慢减少。 针对共享停车中的O-users与P-users在停车时间上冲突的问题,构建了考虑两大场景下的需求分析模型,分析了不同策略下的两类停车需求用户的确定保留车位数量、变更共享策略时间以提高泊位共享率与管理者的净收益,得到如下结论。 (1)当管理者拒绝用户冲突时,随着离开速率增加,变更共享策略时间也逐渐延后,当O-users的返回速率与离开速率相近时,变更共享策略时间逐渐趋于稳定。 (2)当管理者可接受一定概率用户冲突时,随着居住区共享停车场内总车位数量的增加,可将变更共享策略时间提前。 (3)停车收费价格与管理者的净收益始终为正相关关系,而对共享率与变更共享策略时间无明显影响。 (4)管理者接受用户冲突概率增加时,可将变更共享策略的时刻延后以增加自身的净收益。但是,一旦用户冲突的概率过大,亦会出现停车共享机制将难以运营的情况。 假设的O-users的返回速率为固定值以及返回速率服从泊松分布。后续研究中,可根据实证调查数据对O-users的返回规律进行拟合量化分析,进而制定相应的停车场实施共享停车的运营方案。

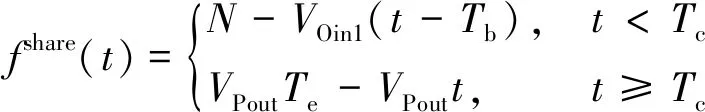

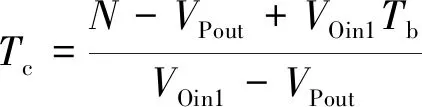



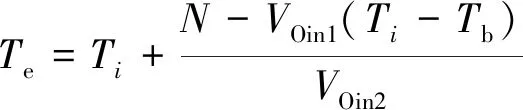
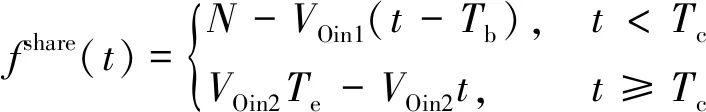

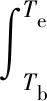
1.2 允许用户冲突场景下的运营策略分析


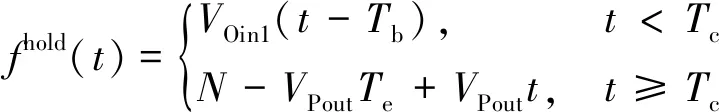
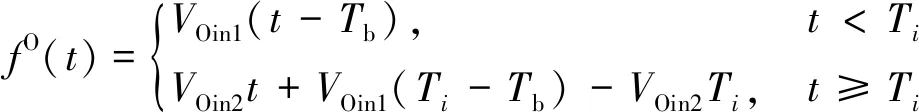
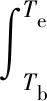
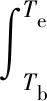
2 数值模拟分析
2.1 拒绝用户冲突时的固定速率数值模拟分析






2.2 允许用户冲突时的速率服从泊松分布数值模拟分析


3 结论

