基于点云模型的大吨位转体桥梁高效称重

巴怀强， 李 超， 孙 凯， 胡兆峰， 周 银

(1.云南昆楚高速公路投资开发有限公司， 昆明 650000； 2.重庆交通大学土木工程学院， 重庆 400074)

中国桥梁的转体施工技术可追溯到20世纪40年代，通常是由于桥位处施工场地的限制或者为了避免影响正常交通，需要将桥梁进行转体施工跨越既有的铁路和高速公路。随着中国交通运输量需求的急剧增加，转体桥梁的顿位也在不断刷新记录，但是转体桥梁的自重越大，在其转体过程中对平衡控制则越难，理论桥梁在设计时其跨中左右两侧的桥体质量是相同的，但由于胀模溢浆及浇筑混凝土时不能保证完全相同的质量等原因，跨中两侧可能不平衡。通常为保障大吨位桥梁在转体过程中的安全与平稳，需要进行称重实验来确定桥梁的偏心情况，并加以配重保证转体平横和中心球铰主要承重，同时确定球铰的摩擦系数及启动牵引力等参数。上述这些关键参数的确定必须基于一个较为准确的桥梁自重，而往往项目中所得到桥梁自重通常是一个理论值。在施工误差和各种环境因素导致的桥梁外观形变下，该值与实际桥梁的自重参数存在一定的差异性，可能影响不平衡力矩的可靠性，从而影响整个桥梁的转体平衡[1]。

中国学者已经在提高桥梁转体的平衡性和精确性上开展了大量研究。颜华惠等[2]对现行称重实验测量球铰静摩阻力进行了改进。翟鹏程等[3]通过考虑初始偏心距，对称重实验原理进行改进，运用实际工程实验进行了计算分析。车晓军等[4]应用基于球铰应力差法对T构转体桥不平衡力矩进行预估，所得精度较为可靠。上述研究在一定程度上保障了桥梁的转体平衡和施工安全，但是均采用的是理论桥梁自重值，并未考虑其是否与桥梁的实际自重相符[5]。

基于此，现通过基于三维激光扫描和BIM(building information modeling)逆向建模技术高效精确的获取大吨位转体桥自重和不平衡力矩。将利用三维扫描技术现实捕捉特点，获取与实际桥梁高度相符的点云模型。通过点云预处理和后处理拟合算法提取点云的特征数据，并依据所提取的特征数据得到转体桥的逆向BIM模型和自重，最后将逆向BIM模型导入实体有限元分析软件计算其不平衡力矩。该方法将进一步保障大吨位桥梁在转体过程中各项参数的可靠性与安全。

1 研究背景及路线

1.1 研究背景

依托昆明(岷山)至楚雄(广通)高速公路项目，以大德大桥为研究对象。该桥横跨成昆铁路，为了避免影响既有铁路线的营运安全，因此需采用平转法转体施工，且要求在短时间内完成桥梁转体。该桥转体理论自重约为1.5×104t，是云南省的第二大吨位转体桥。大桥全长290 m，主桥转体部分长106 m，桥面宽33.5 m，双向六车道。对整幅进行转体，将T构逆时针方向转体66°至成桥位置，如图1所示。

图1 大德大桥现场Fig.1 Site of Dade Bridge

1.2 技术路线

现提出一种利用三维激光扫描和BIM逆向建模技术进行转体桥自重和不平衡力矩计算的新方法，其技术路线如图2所示。

2 转体桥梁点云采集与预处理

2.1 扫描仪及其参数介绍

采用Leica ScanStation P50地面三维激光扫描仪(图3)，该扫描仪在保持高精度情况下，拥有长达1 km的扫描距离，该扫描仪被广泛的应用于水利水电、矿山地质、地形勘测、灾害应急等领域[6-7]。扫描仪采用精密双轴补偿技术，精度极高，可实时补偿仪器轻微震动所带来的精度偏差，使得仪器既可在高速旋转提高扫描速度的同时，又能保证其扫描精度。无论是在光照较强的白天、光线不足的夜间扫描仪均可以获得目标对象表面的三维坐标信息并完成扫描工作。该扫描仪在不同模式下基本技术参数如表1所示。

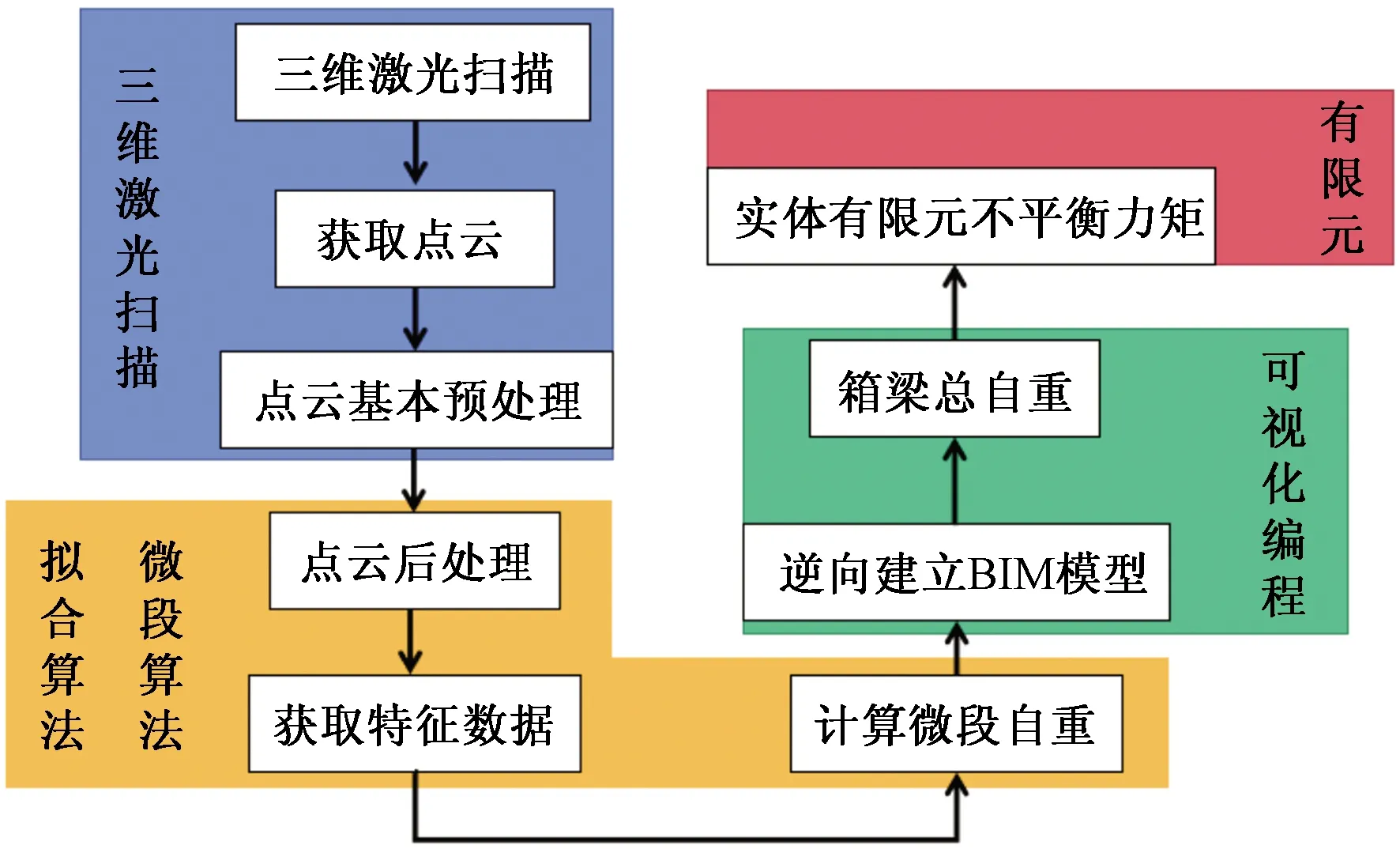
图2 技术路线Fig.2 Technical route

图3 Leica ScanStation P50扫描仪Fig.3 Leica ScanStation P50 scanner

表1 4种扫描模式下的技术参数

2.2 数据采集方案

转体桥内外扫描虽然在数据采集和处理上增加了一定的难度，但最终所得到的点云模型更加逼近真实桥体。为保证桥体内外点云模型能够精准采集和拼接，需根据现场实地勘察分析，布设球型标靶，在保证内外均能通视标靶的情况下，再定位外部扫描测站点，具体技术路线如图4所示[8]。

根据现场实际情况分析之后，标靶位置定位在桥体两端的各个空腔角点处，前后两端每个空腔交叉布置两个标靶，也就是每个空腔由4个球型标靶进行定位控制，使每个空腔都能够依次与外部点云模型独立拼接，为了保证外部扫描桥面点云的拼接精度，同样在前后两端设置2个球型标靶，如图5所示。转体桥周围不再设置标靶，其各个测站点的点云拼接依靠点云重合度自动拼接。

图4 桥体内外扫描技术路线Fig.4 Technical route of scanning inside and outside the bridge

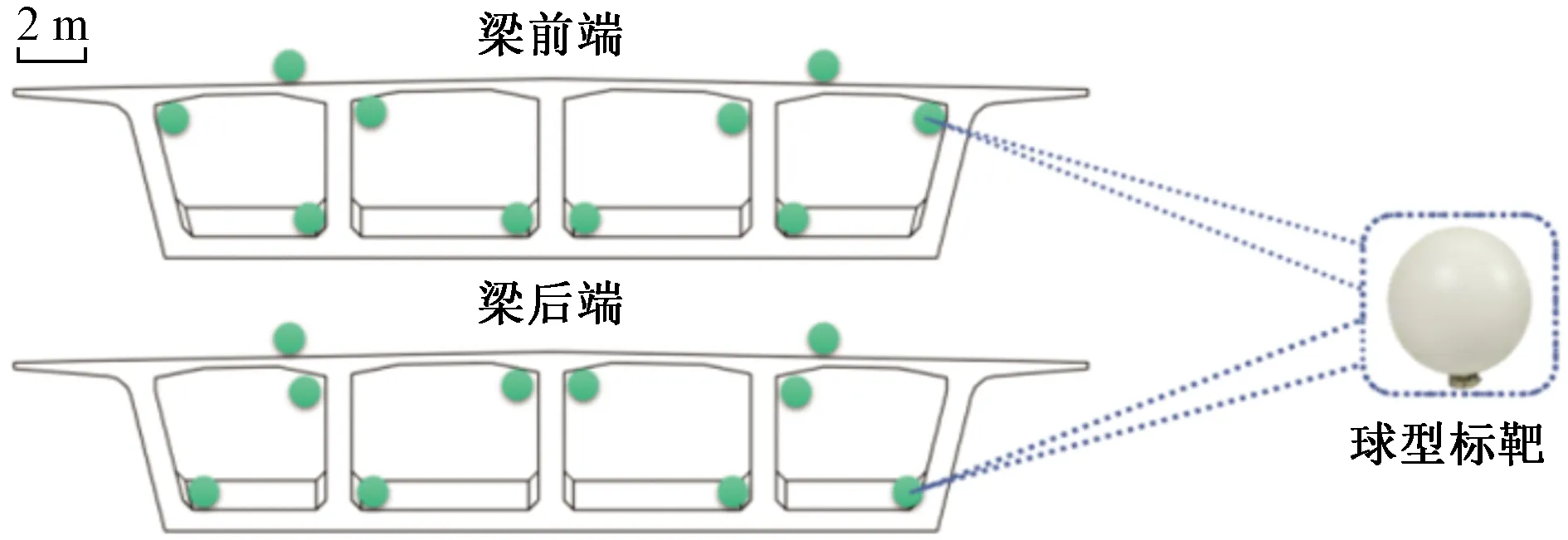
图5 球型标靶布置Fig.5 Layout of spherical target

最后再确立外部和内部扫描测站点的布设，其中外部测站点桥周围共设置6个点，保证各个测站点的点云通视且达到重合度要求，以及扫描到两端的球型标靶；桥面共设置2个测站点，每个站点都需要扫描到桥面的4个球型标靶。内部扫描共设置了12个站点，每个空腔3个站点，保证各空腔内测站点与球型标靶通视即可，内外测站点布设如图6所示。

2.3 点云数据预处理

在完成前期各测站点云扫描之后，所采集得到的点云数据均带有大量与目标点云无关的噪声点和冗余点。因此在进行点云拼接和其他后期处理工作前，首先要进行无关点的删除和点云降噪工作，具体预处理技术流程如图7所示。在无关点的删除中主要包含目标对象周围的场景点云，桥面上的预留的护栏及钢筋点云，跨中转体支撑，以及空腔内部的齿块点云。这里需要注意的是去除护栏、齿块、跨中转体支撑的点云是为了后期的计算效率，对总结果影响较小。

图6 内外站点布置Fig.6 Layout of internal and external stations

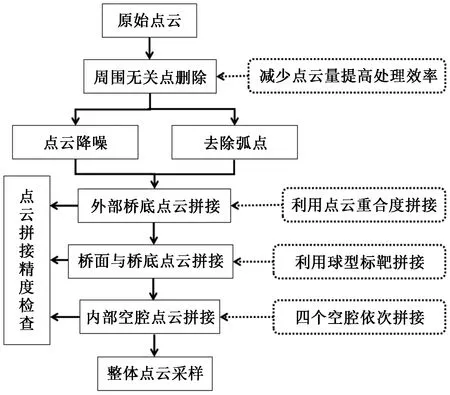
图7 原始点云预处理流程Fig.7 Preprocessing process of original point cloud

在点云拼接过程中，无论是依据重合度还是球型标靶，每次拼接完成之后都需要检查点云拼接的精度，避免两两子部分点云之间出现“点云分层”的现象，之后进行点云采样进一步降低点云量，最终拼接后的完整点云如图8所示。

3 点云切片与拟合

3.1 点云切片处理

在箱梁点云在进行点云切片之前，需要计算点云的平均密度(ρ)，从而在保证特征完整的情况下确定点云切片的厚度(Δ)。利用邻域查询思想来计算平均密度(ρ)，从点云中随机选择b个点F1，F2，…，Fb作为查询对象，以每个查询对象Fi作为圆心，半径为R的圆作为一个范围阈值，如图9所示，查询范围内的点数PFi，则Δ的取值应满足[9-10]：

(1)

式(1)中：栅格内点数N的取值越大则特征保留的越完整，但切片的厚度Δ将随之变大，将会影响切片处理的效率。因此需要依据点云的实际情况，选择合适的N值和切片的数量。箱梁在切片时是按照梁底的变化的曲率和空腔内部的结构变化进行的，跨中70 m长为加密区，两端各18 m为非加密区，如图10所示，加密区的切片厚度Δ1为20 cm，非加密区切片厚度Δ2为40 cm，共计440个点云切片。

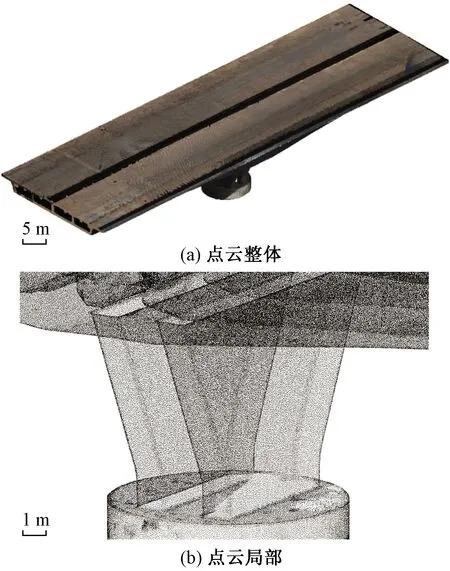
图8 内外点云拼接完成Fig.8 The splicing of internal and external point clouds is completed

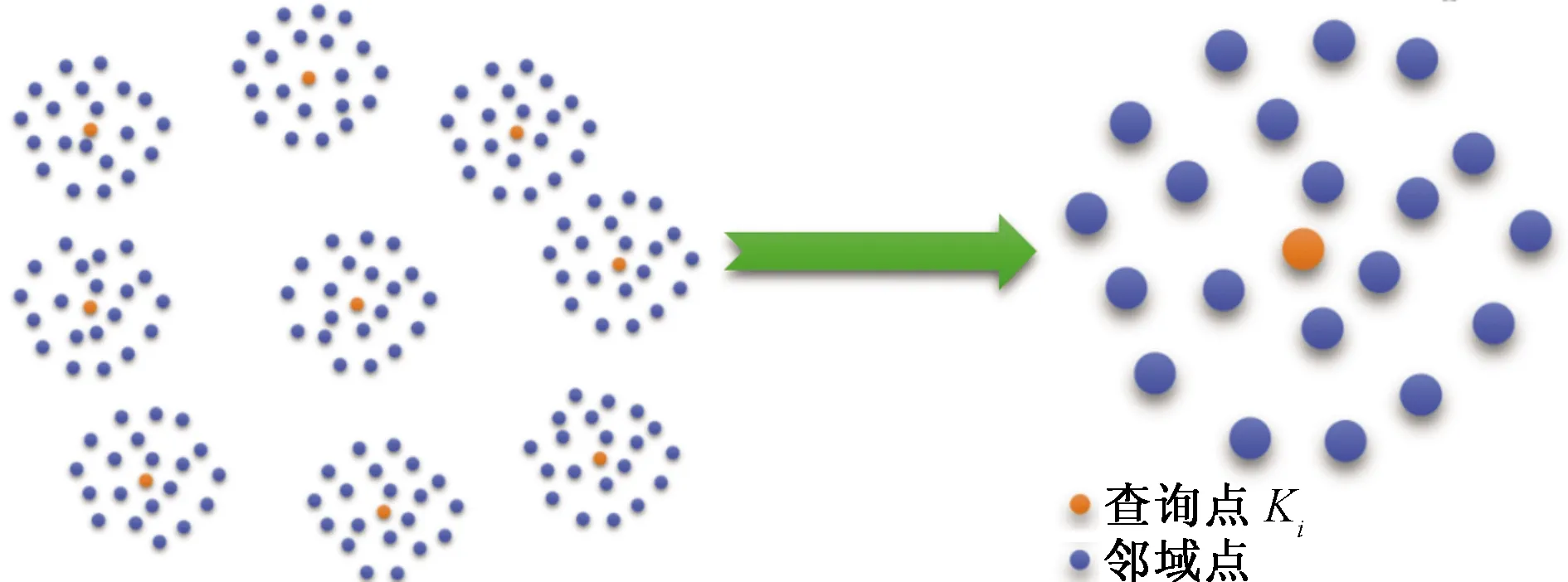
图9 邻域查询Fig.9 Neighborhood query

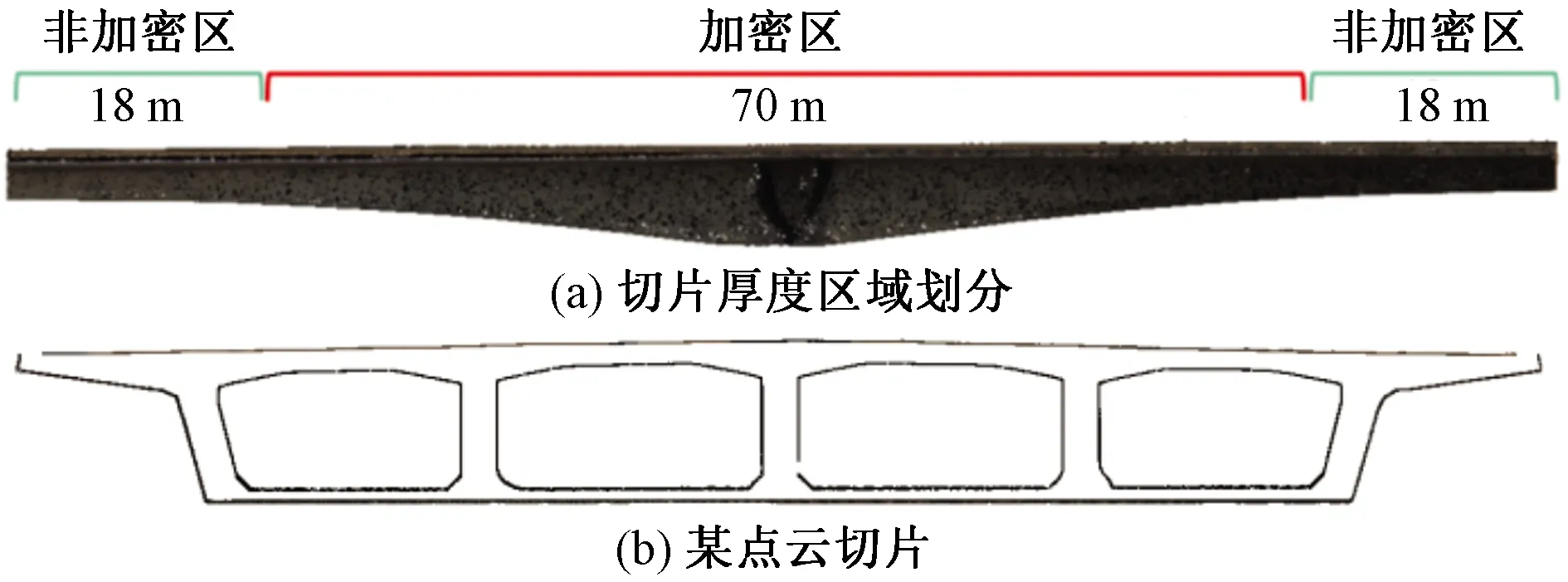
图10 切片厚度区域划分和某点云切片Fig.10 Slice thickness area division and cloud slice of a point

3.2 特征拟合

在箱梁点云切片的特征拟合过程中，利用点云聚类将每个切片划分为1个外轮廓和4个内轮廓。在轮廓的拟合中，提出了轮廓自动拟合算法，主要步骤如下。

(1)随机选择种子点P1。

(2)计算与种子点P1最近的点P2，P2点将作为种子点再次其最近的点P3，依次进行遍历所有点后，按照欧式距离进行点排序。

(3)选择合适的栅格尺寸，统计栅格内点数N，设置判断条件跳过点数低于M的栅格，利用RANSAC算法拟合复合条件的栅格点并求出其斜率Ki。

(4)统计所有的Ki并进行排序，利用斜率和已知点，求出各个直线的交点坐标，相邻交坐标进行连线形成闭合轮廓线。

图11 箱梁某切片轮廓拟合图Fig.11 Contour fitting of a section of box girder

为了能够在图11中清楚展示拟合线、相交点、点云三者之间的关系，图11中的红色圆圈点云是经过倍数采样后的点云。

4 自重与不平衡力矩计算

4.1 微段自重计算

为了直观地看出实际状态下桥梁体积中心左右的不平衡性，以及快速锁定自重差值变化最大的截面位置，需计算箱梁各个微段的自重。在微段自重求解算法中借助微分思想，箱梁各点云切片相当于微分段。拟合所得到的点云切片轮廓均为闭合的，利用每个闭合形状的面积作为一个微分段底面积(S)，其长(L)等于点云的切片厚度(Δ)。即箱梁自重的计算变为底面积(S)的计算，无论是内轮廓还是外轮廓，其闭合形状均为多边形，尤其是外轮廓的形状更为复杂。

(2)

式(2)中：Vi表示i=1,2,…,45的微段体积；Vj表示j=46,47,…, 395的微段体积；Vk表示k=396,397,…,440的微段体积；V=Vi+Vj+Vk；Li表示i=1,2,…,45的微段长度；Ljj=46,47,…, 395的微段长度；Lk表示k=396,397,…,440的微段长度；M表示转体桥质量；SOL表示外轮廓左侧部分面积；SOR表示外轮廓右侧部分面积；i=1,2,…,45；j=46,47，…,395；k=396,397，…,440；ρ=2.6 t/m3。

依据所得到微段的体积，求出箱梁理论设计图纸所对应位置的内外轮廓面积和体积V，两者进行对比，能够快速锁定因施工误差或其他因素导致的截面变形的位置，如图13所示，图13中展示的理论和拟合值为每间隔10个微分段所取的值。

从图13可以直观地看出，依据箱梁图纸所计算出来的微段体积呈现轴对称的理想体积，理想状态下其桥梁的转体是平衡的，不存在偏心矩。但是实际的状态的下的体积并不是轴对称的，而且中心两侧明显不一致。

图12 外轮廓截面划分示意图Fig.12 Outline section division diagram

图13 理论与拟合体积对比Fig.13 Comparison of theoretical and fitting volume and difference

4.2 不平衡力矩计算

为了进一步保持转体的平衡和安全，必须精确计算不平衡力矩参数。需借助实体有限元分析软件进行计算，但是与传统方法不同的是，所代入有限元的模型是依据前期提取到的特征数据逆向创建的BIM模型，该模型与实际桥梁状态高度相符。

在逆向BIM模型的建立过程中，为了提高建模的质量和效率，采用Dynamo可视化编程软件进行模型的创建。通过Dynamo调取点云特征参数，利用Dyanmo中Excel.ReadFromFile 节点则可将数据文件中特征数据导入到 Dynamo 中，简单的数据行列变换之后，利用 Point.ByCoordinatesshe 节点生成三维点坐标，再由点生成闭合轮廓线，最后由闭合轮廓线放样生成箱梁实体模型，如图14所示。

图14 逆向箱梁BIM模型Fig.14 BIM model of reverse box girder

将逆向BIM模型导入实体有限元计算软件Midas FEA进行计算分析，求出最后的不平衡力矩如表2所示。

5 结论

以云南省大吨位转体桥——大德大桥为研究对象。提出并验证了基于三维激光扫描和BIM逆向建模技术高效获取转体桥自重和不平衡力矩的新方法。得出如下结论。

表2 转体桥参数

(1)借助三维激光扫描技术现实捕捉的特点，通过现场布置球型标靶与点云重合度相结合的方法，实现了转体桥内外点云高精度拼接，获取到与实际桥梁状态高度相符的点云模型。

(2)利用所提出的边界拟合与微分自重算法计算出了可靠性较高的微段自重，不仅可以直观看出实际状态下桥梁的体积中心左右的不平衡性，而且可以快速锁定差值变化最大的截面位置，也可将各个截面的实际变形情况作为转体桥的初始截面形变数据进行保存。

(3)利用可视化编程逆向创建出实体有限元计算所需的实际状态模型，成功得到转体桥梁的不平衡力矩。

可见，本文方法在计算实际状态下大吨位转体桥的自重和不平衡力矩参数，具有一定的实际工程意义和价值，进一步拓展了三维激光扫描和BIM技术融合的应用场景。