基于PEST的高坝枢纽区岩体稳态渗流场反演分析

王一凡，徐毓威，曾 俊，于 浩，潘中祺

（1.武汉大学水资源与水电工程科学国家重点实验室，武汉430072；2.武汉大学水工岩石力学教育部重点实验室，武汉430072；3.长江勘测规划设计研究有限责任公司，武汉430010）

0 引 言

裂隙岩体的渗透系数是研究地下水运动［1］、污染物迁移［2］的重要水文地质参数，也是渗流分析与计算中的关键参数，其取值对于水利水电工程的设计与安全评价具有重要影响［3，4］。在工程实际中，岩体的渗透特性参数通常采用现场水文地质试验方法来获取，如压水试验、抽水试验、微水试验等，但由于技术和经济条件的制约，通常仅在某些重点部位开展，因此研究渗流过程中岩体渗透系数的确定方法具有重要意义。

在工程施工与运行过程中，通常会积累较为丰富的渗流与渗压监测资料，基于渗流、渗压资料开展渗流场的反馈分析研究已较为广泛［5］，例如李守巨等［6］在渗压和渗流量观测值基础上，采用Levenberg-Marquardt 优化BP 神经网络，反演得到了工程枢纽区岩体及混凝土帷幕的渗透系数取值；刘武等［7］基于正交设计、有限元正分析、BP神经网络、遗传算法建立起了多目标非稳定渗流反馈分析方法，解决了长河坝水电站基坑涌水问题。

Pest（Parameter Estimation）是由澳大利亚Water Numerical Computing咨询公司John Doherty开发的独立于模型的非线性参数估计与不确定性分析程序［8，9］，近年来在地下水与土壤水运动模型中应用较为广泛。Elcl 等［10］使用PEST 程序确定了地下水模型（MODFLOW）的水力学参数，研究了土耳其伊兹密尔地区地下水污染物的扩散规律；Fang［11］等在Root Zone Water Quality Model（RZWQM）模型中估算了土壤水力学参数，发现该程序在参数寻优方面具有高的效率；胡丹等［12］在MODFLOW-HY‐DRUS 耦合模型中对水文地质参数和土壤水力学参数进行优化，显著提高了模拟精度，但是该程序在水电工程岩体渗流分析中的应用较少。

本文根据在工程实际中两类常用的渗流场监测数据：渗流量与渗压构建目标函数，采用PEST 程序结合含自适应罚函数的Signorini 变分不等式渗流分析方法［13］，建立起了一种全新的渗流场反馈分析方法，并通过一个简单算例，验证了该方法的可靠性，并成功地将该方法应用于我国西南某水电站岩体稳态渗流场分析，取得了良好的拟合效果。

1 稳定渗流理论及其反问题

1.1 稳定渗流分析基本方程

在水利水电渗流计算中，由于岩体裂隙网络的复杂性，通常采用连续介质力学方法。在不考虑岩土体变形以及流体的可压缩性情况下，流体的连续性方程可表示为：

考虑岩土体中流体运动服从达西定律，结合式（1）可得到岩土体渗流控制方程：

式中：h=h（x，y，z）为代求水头函数；Kx、Ky、Kz分别为x、y、z方向的渗透系数。

基于式（2）的控制方程求解实际渗流问题时，通常会涉及以下4类边界条件。

（1）水头边界条件。

（2）流量边界条件。

（3）出渗面Signorini型互补边界条件。

式中：Γs为潜在出渗边界。

（4）自由面边界条件。

式中：Γf={(x，y，z)|ϕ=z}为自由面，即湿区与干区的分界面。

1.2 稳定渗流反问题表述

假设在稳定渗流计算中需要确定的岩体渗透系数有X组，而通过监测仪器获得的渗压和渗流量数据分别为M、N组，那么稳定渗流的反问题可以表述为：在待确定的岩体渗透系数的范围内，寻找一组最优的组合，使得由渗流量和渗压值构成的如下目标函数最小：

式中：Φ为目标函数；Hi和分别为第i支渗压计测点的计算水头与监测水头；Qj和分布为第j条排水廊道测点的计算流量与监测流量；wH与wQ分别表示渗压权重系数与流量权重系数。

2 PEST参数优化算法

PEST 程序是介于高斯牛顿法与梯度下降法之间的一种非线性优化方法，同时具备高斯牛顿法的快速收敛性和梯度下降法的全局搜索性，能够在多维的参数空间内优化模型输入参数。该程序主要基于高斯-马奎特-列文伯格（Gauss-Marquart-Levenberg）算法，对模型的输入参数进行优化调整，进而求取目标函数（模型计算值与实际观测值的差异函数）的最小值。具体过程如下：

假定n个模型输入参数存储于向量x中，m个模拟值存储于向量y中，则向量x与向量y的关系为：

式中：M为模型输入参数与模拟值相关联的非线性函数。

将y=M（x）在参数初值及其计算值（x0，y0）处通过一阶泰勒公式展开得到：

带入雅可比矩阵表示为：

式中：矩阵J是y=M（x）在x0处的雅可比矩阵，大小为m行n列，记录了n个模拟值分别对m个模型输入参数的偏导数。

定义参数反演的非线性目标函数为：

式中：y1是模拟值y对应的真实值；w为相应的权重向量。

由于对（8）式以一阶泰勒公式展开，要求x-x0足够小，所以参数优化过程需要不断更新参数向量x和雅可比矩阵J，使得目标函数最小，定义参数更新向量：u=x-x0，结合（11）式可表示为：

3 算例验证

为了验证PEST 反演算法的有效性与可行性，本文参考武晓炜等［14］使用GA-BP算法开展的研究论文，建立了同样的土石坝二维模型［14］，模型共有单元5 768个，节点9 459 个，上游水位40 m，如图1所示。其中，I 为坝体、Ⅱ为防渗帷幕、Ⅲ为第一层基岩、Ⅳ为第二层基岩，依据工程类比设置4类材料的渗透系数理论值分别为2.0×10-3m/s、6.0×10-7m/s、6.5×10-4m/s、1.0×10-6m/s，参数反演变化范围以理论值为中心，上下跨越两个数量级。模型内总共布置了3个渗压计P1、P2、P3和一个量水堰Q1。

为了确定4类材料的渗透系数，本文分别采用了PEST程序和GA-BP 算法进行反演分析。其中，在反演过程中，采用GABP 算法需要对每个参数设计7 个水平的49 组正交试验和10 组均匀试验，并基于参数输入、渗流量与渗压输出数据，通过反复试算确定了4-9-34-4 的神经网络结构，最终通过遗传算法进行优化；而采用PEST 程序，只需直接调用模型计算63 次，就能完成参数优化。基于两种算法获得的参数优化结果如表1所示，由表可以看出，在相同的参数变化范围内，采用PEST 法获得的4 种材料渗透系数值同理论值的相对误差分别为0.61%、0.78%、0.69%、0.69%，均不超过1%，并且小于GA-BP 法的相对误差（2.00%、1.50%、6.15%、9.00%）。所以，同GA-BP 法相比，PEST 反演算法不仅在过程上直接简便，而且具有更高的准确度。

表1 待反演参数设置与优化结果

4 工程实例

为了研究PEST 参数反演算法在大型水利水电工程渗流分析中的适用性，本文以我国西南某水电站为背景，对其2014-2015年的蓄水周期内渗流计算过程中涉及的岩体渗透系数开展反演分析。

4.1 工程概况

该水电站位于金沙江上游高山峡谷段，谷底宽阔平缓，两岸山体陡峭雄厚，河谷呈典型的对称“U”型结构。工程枢纽区由混凝土双曲拱坝，泄洪消能设施及两岸引水发电建筑物等组成，最大坝高285.5 m，正常蓄水位600 m，装机容量12 600 MW，坝段控制流域面积占金沙江的96%，约为45.44 万km2。

坝区河床基岩及两岸边坡岩性主要为二叠系上统峨眉山玄武岩，下部埋藏二叠系下统茅口组石灰岩，玄武岩与灰岩间夹有2～3 m厚的泥页岩夹层。枢纽区主要地质构造为层间和层内错动带，整体上岩体性质较好，左右岸各发育有12 条层间错动带，其平均厚度约为0.1～0.6 m。依据钻孔压水数据，并考虑岩体的风化程度随埋深增加而减弱，可人为地将玄武岩划分为中等透水，弱透水上段、弱透水下段、微微透水、新鲜岩体等5个渗透分区，如图2所示。

4.2 有限元模型

根据该水电站枢纽区的工程地质条件、水文地质条件和枢纽布置情况，考虑到工程左右岸属于独立的地下水流动系统，本文建立了该水电站右岸三维有限元模型如图3所示，模型共划分实体单元433 万个，节点134 万个，上下游相距3 220 m，右边界距河床中心线约1 775 m，底部高程-180 m。同时，采用排水子结构技术［15］对厂坝区防渗排水系统进行了精细模拟，如图4、图5所示。为了开展厂坝区三维渗流场计算，设置模型的边界条件具体为：上下游库水和河水淹没范围内的节点取定水头边界；右岸山体侧边界与下游侧边界取隔水边界；将与底层廊道相连向上汇水的溢流型排水孔设置为定水头边界；其他排水廊道内排水孔设置为Signorini型潜在溢出边界。

4.3 反演计算

考虑到枢纽区岩体的风化程度差异，结合地质勘测资料与工程施工情况，本研究设置了强风化，弱风化上段、弱风化下段、微风化、新鲜岩体、灰岩、泥页岩夹层、混凝土材料、防渗帷幕、厂房开挖扰动区等共计13 个待反演渗透系数，并依据有关钻孔压水试验结果与工程经验合理设置待反演渗透系数上下限、各向异性比值，同时选取厂坝区具有代表性的排水廊道6条（厂区5条、坝区1条）、渗压计14支（厂区6支，坝区8支）分别作为渗流量监测点和渗压监测点，其空间布置如图4所示，并由这些监测点数据共同构成参数反演目标函数。

由于水库的蓄水过程会导致区域水文地质条件的显著改变，而岩体的渗透系数可能会受到水力耦合效应的影响而产生一定程度的变化，因此本文仅针对该水电站的2014-2015年的蓄水周期内渗流场特征，以上游库水位在600 m 正常蓄水位时作为计算工况，利用PEST 程序对设定的13 个待反演参数进行优化，参数设置与优化结果如表2所示。

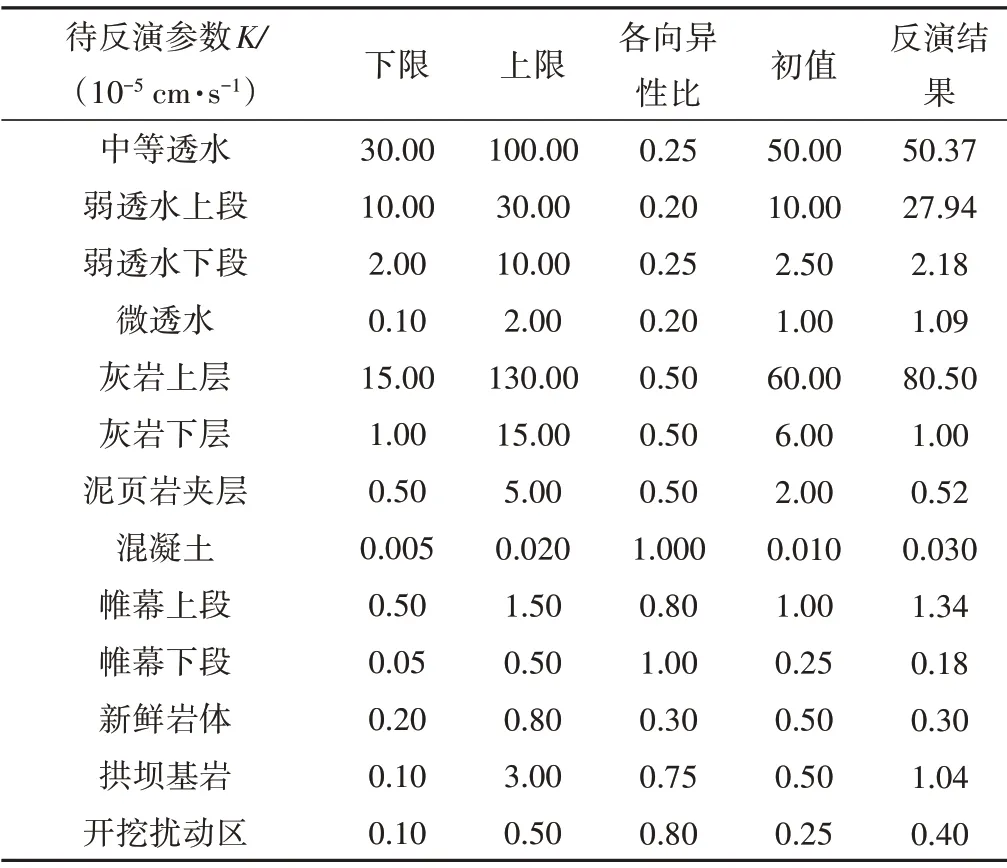
表2 待反演参数设置与优化结果

反演过程中目标函数变化曲线如图6所示，该图表明在总计7 次迭代，调用模型114 次过程中，目标函数呈现逐次递减的趋势，并且具有快速收敛性。

依据PEST 程序参数反演获取的渗透系数，本文分别对库水位为550、560、570、580、590、600 m 的渗流场特征进行了模拟。其中排水廊道内流量测点计算值与实测值对比如图7所示，结果表明计算值与监测值总体吻合较好，其中厂区渗流量明显高于坝区，并且同上游库水位具有一定的相关性，但是由于部分量水堰的埋藏深度与位置的差异会使得流量监测数据具有较大的离散性，导致计算值与监测值的差别相对较大，如Q1、Q4等。

厂坝区代表性渗压测点的计算值与实测值对比如图8所示，二者同样吻合较好，其中帷幕前渗压计（P1）与上游水位呈明显的相关性，且变化幅度较大，而帷幕后渗压计的水头由于受防渗帷幕和排水孔幕的控制，波动较小，较为平稳。

为了评价反演结果的准确性与可靠性，本文选取了3 类广泛用于时间序列预测模型结果检验的误差评估指标：平均绝对误差MAE、均方根误差RMSE，平均绝对百分比误差MAPE，其表达式如下所示：

式中：Pi是第i个工况下的模型预测值；Hi是第i个工况下的模型实测值，N计算工况总数。

利用上述的3 类误差评价指标，对研究工况下的渗流量测点与渗压测点的计算结果展开了误差分析，如图9、图10所示。结果表明，各工况下的渗压测点的MAE、RMSE、MAPE三类指标均不超过6 m、6 m、2%；流量测点的MAE、RMSE、MAPE三类指标基本不超过2.5 L/s、2.5 L/s、25%，依据相关工程经验，能够认为反演计算得到的参数是准确和可靠的。

5 结 论

本文基于PEST 参数率定程序，结合含自适应罚函数的Signorini 变分不等式渗流分析方法，依据特定时间序列内的渗流量与渗压监测数据构建的目标函数，建立了一种对岩体渗流参数进行反演分析的方法，并成功应用于实际工程。并通过采用平均绝对误差MAE、均方根误差RMSE，平均绝对百分比误差MAPE等三类误差评价指标对根据反演参数获得的渗流量与渗压计算值与监测值偏差进行分析，结果表明，流量测点的MAE、RMSE、MAPE三类指标基本不超过2.5 L/s、2.5 L/s、25%；该工程渗压测点的MAE、RMSE、MAPE三类指标均不超过6 m、6 m、2%，进而证明了本文提出的反演方法的可靠性与准确性。 □