EEMD多尺度熵和ELM在水电机组振动信号特征提取中的应用

何葵东，陈 伽，金 艳，蒋文君，肖志怀

（1.湖南五凌电力科技有限公司，长沙410004；2.五凌电力有限公司株溪口水电厂，湖南益阳413599；3.武汉大学动力与机械学院，武汉430072）

0 引 言

水电机组运行环境不断复杂化，其运行的安全性与稳定性越发受到众人关注［1］。水电机组的运行稳定性通过机组振动信号特征体现，大部分故障由机组振动引起［2］。研究机组振动特性，准确提取机组振动信号中的特征，有效进行机组状态评价和故障预警，进而实现故障诊断并及时对机组进行检修与维护，能一定程度上延长机组寿命，为企业带来巨大的经济效益［3］。

水电机组本质上是多因素耦合的复杂系统，运行过程中同时受水力、机械和电磁因素影响，引发机组振动故障［2］。特征提取的目的在于将原始信号中表征机组实际状态的特征准确提取，这对于机组状态评价和故障预警具有重要意义［4］。针对水电机组振动信号的非线性、非平稳性和强噪声性，常采用小波变换、变分模态分解（VMD）、经验模态分解（EMD）等时频分析方法进行分析［5］。小波变换和VMD 都为非自适应分解算法，依靠经验性结论选取参数以得到准确分析结果［6］。经验模态分解（Empirical mode decomposition，EMD）根据信号自身特点进行分解，有效避免小波基函数及分解层数的选取，但端点效应及模态混叠问题较为明显［7］。在EMD 的基础上提出的集合经验模态分解（Ensemble empirical mode decomposition，EEMD），有效抑制了端点效应和模态混叠问题［8］，广泛应用于非平稳信号分析中［9-11］。

基于熵理论的特征提取方法近年来在非线性非平稳信号特征提取中多有应用［4］，熵表现了信号序列的复杂程度，将信号的随机性和复杂动力学突变行为转化为统计学指标，更直观地表征信号特征［12］。将先进时频分析方法与熵理论结合的信号特征提取，对于现阶段机械复杂运行环境中所采集的非平稳、非线性信号，具有良好的应用效果。唐贵基等［13］结合奇异谱分解（SSD）和多尺度排列熵（MPE），采用峭度最大原则筛选经SSD分解的滚动轴承振动信号主分量，并计算主分量MPE，采用K 近邻（KNN）进行模式识别，有效提取了滚动轴承特征。苟先太等［14］对高速列车横向减振器振动信号进行变分模态分解（VMD），计算互信息指标筛选的模态多尺度熵（MSE）特征值，采用支持向量机有效进行了故障判别。程晓宜［15］等构造水电机组振动信号时域、频域特征和EEMD 样本熵多维特征，经遗传算法对高维特征进行降维处理后，分别输入支持向量机、反向传播神经网络和朴素贝叶斯分类器进行融合诊断，有效提高了诊断准确率。张炜博［16］采用快速集合经验模态分解（FEEMD）分解水电机组振动信号，计算各IMF 分量的精细复合多尺度散布熵作为特征向量，采用最大相关最小冗余（mRMR）方法进行特征简约后输入随机森林分类器实现水电机组振动故障识别。

本文提出基于EEMD 和MSE 的水电机组振动信号特征提取方法，采用ELM 实现模式识别。对降噪后水电机组振动信号进行EEMD 分解，并根据峭度—标准相关系数指标筛选有效本征模态分量（IMF），计算有效IMF 的MSE 特征值并构建特征向量集，将故障特征集输入ELM 后，有效评价机组运行状态，实现机组故障预警，为后续具体故障判别做好了充分准备。本文对机组实测振动信号进行了特征提取，并采用EEMD 样本熵方法作为对比试验，结果表明，本文所提方法对于水电机组振动信号特征提取具有普适性且应用效果更优。

1 基本原理

1.1 EEMD算法原理

EEMD 算法由Wu 等［8］提出，该算法在EMD 基础上应用了噪声辅助分析，白噪声的加入增强了模态的抗混叠性［17］。白噪声具有频率分布均匀的统计学特性，该特性弥补EMD方法所存在的模态不连续缺陷，改进极值点特性，进一步抑制了模态混叠现象；同时，EEMD 在分解过程中对各模态多次取平均，使得噪声相互抵消，抑制了噪声的影响［8］。

EEMD算法的计算过程如下［7，8］：

（1）将一定噪声等级的高斯白噪声ni(t)加入原始信号x(t)中，得到待处理信号xi(t)：

（2）对xi(t)进行EMD 分解，得到各阶IMF 分量cij(t)和对应残余分量ri(t)：

式中：cij(t)为第i次加入白噪声后分解得到的第j个IMF分量；m为IMF分量的个数。

（3）重复M次步骤（1）～（2），对各阶分量取平均，得到最终IMF分量cj(t)为：

式中：M为添加白噪声的次数即总体平均数，通常取值范围为100～300。

（4）信号x(t)经EEMD分解最终结果为：

式中：r(t)为信号x(t)经EEMD分解后得到的残余分量。

实验研究表明，在处理非平稳非线性信号时，噪声等级k=0.2，总体平均数M为100时，具有较好地处理效果［6］。本文选取噪声等级k= 0.2，总体平均数M= 100。

1.2 多尺度熵原理

多尺度熵（Multi-scale entropy，MSE）算法最先由Costa［18］等提出，该算法基于样本熵，从不同尺度描述时间序列的不规则程度。通过对原始数粗粒化处理，计算得到数据序列在多个尺度下的样本熵［18］。对于相同尺度下的不同数据序列，样本熵值高的序列具有更高的复杂性，由此体现数据序列之间的差异性［19］。对于给定原始数据序列X={x1，x2，…，xL}，L为序列长度，其多尺度熵的由以下步骤计算得到［20］：

（1）采用粗粒化算法处理原始序列，得到新的时间序列：

式中：j= 1，2，…，N，τ为尺度因子，每一个粗粒化后的时间序列的长度N=L/τ，τ= 1时即为原始序列。

（2）将粗粒化序列组成一组m维矢量：

式中：i= 1，2，…，N-m+ 1。

（3）定义Y(τ)(i)与Y(τ)(j)的距离为d[Y(τ)(i)，Y(τ)(j)]，计算公式如下：

式中：i，j= 1，2，…N-m+ 1，j≠i。

（4）给定阈值r（r称作容差，r＞0），对于每个i≤N-m+ 1的值，统计d[Y(τ)(i)，Y(τ)(j)]＜r的数目H与距离总数N-m+1的比值，记作Cτi，m(r)，其平均值记作Cτ，m(r)：

（5）增加维数至m+ 1，重复步骤（2）～（4），从而得到尺度为τ，嵌入维数为m+ 1时的Cτi，m+1(r)，求其平均值得到Cτ，m+1(r)；

（6）当N为有限数，尺度为τ时，定义样本熵为：

多尺度熵由不同尺度的样本熵组成集合，表示为：

多尺度熵的计算需确定嵌入维数m、相似容限r和尺度因子τ三个参数，一般情况下，m= 2，r= 0.1～0.25δ（δ为原始数据序列的标准差），τ≤20［18］。本文选取m= 2，r= 0.2δ，τ= 15。

1.3 极限学习机理论

极限学习机（Extreme Learning Machine，ELM）网络由Huang G B 等［21］提出，ELM 的本质是单隐含层前馈神经网络（Single Hidden Layer Feedforward Neural Networks，SLFN），该算法的输入层与隐含层的权重及隐含层偏差是随机分配的，训练过程中无需再进行调整，通过隐藏的简单广义逆运算来分析确定SLFN 的输出权重，对于梯度下降学习算法中训练速度慢，易陷入局部极小值，学习率敏感等问题，能一一避免［16］。只设置隐含层神经元个数这一学习参数，就能得到唯一最优解。相较于传统的学习方法，ELM 的学习速度更快，易于实现，且泛化能力更强［22］。

任意给定N个不同的学习样本集(xi，yi)，1 ≤i≤N，其中xi∈Rm，yi∈Rn，设隐含层有L个神经元，激活函数为g(x)，则网络训练模型如图1所示［23］。

图1中，输入层的m个神经元和输出层的n个神经元分别对应m和n个变量。网络输出由下式表示：

式中：权值向量βj=[βj1，βj2，…，βjn]T，连接第j个隐含层节点和输出层节点；权值向量ωj=[ω1j，ω2j，…，ωmj]T，表示输入层节点与第j个隐含层节点的输入；bj是第j个隐含层节点的阈值；oj=[oj1，oj2，…，ojn]T，表示网络输出值。

2 特征提取流程

本文提出基于EEMD 多尺度熵和ELM 的水电机组振动信号特征提取方法，采用EEMD 分解降噪后信号，根据峭度—标准相关指标筛选有效模态，计算有效IMF 分量尺度因子为1～15的特征量，分析得到最佳尺度因子的组合特征向量，将特征向量输入ELM进行模式识别。具体特征提取流程如图2所示。

具体步骤：

（1）采集得到水电机组原始振动信号，对信号进行非局部均值降噪处理；

（2）对降噪后信号进行EEMD分解，计算IMF分量峭度及与原信号的标准相关系数，筛选蕴含故障信息丰富且与原信号相关性较强的IMF分量；

（3）计算有效IMF 分量的多尺度熵，并构建最佳尺度下信号高维特征向量；

（4）将特征向量集输入ELM进行模式识别。

3 实例分析

3.1 案例1

XK 电站1 号机组2018年8月，机组顶盖振动出现异常，机组发生不明原因故障。采集得到该机组2018年3月1日至3月24日内的顶盖X向振动波形数据作为正常状态信号，将2018年7月26日至8月20日间采集到的顶盖X向振动波形数据视为故障信号。采样频率为640 Hz，每组数据采样长度为2 048，采集得到两种状态下各50组数据。

对采集到的信号进行信号预处理，所采用方法为非局部均值去噪［24］，经实验，搜索窗口半径设为5，领域窗口半径设置为2，高斯平滑参数设为1时，在达到较好的降噪效果的同时基本保留了原信号的信息。对机组正常和故障状态下的顶盖X向振动波形进行非局部均值降噪处理，信号降噪前后对比如图3所示。

对降噪后信号进行EEMD 分解，噪声等级取k= 0.2，总体平均数取M= 100，正常和故障状态信号经EEMD 分解后的结果如图4所示。根据峭度—标准相关系数指标筛选有效IMF分量，峭度作为一种无量纲参数，能表征信号的受冲击程度，其值越大，信号所蕴含的故障信息越丰富［25］；计算各IMF 分量与原信号的标准相关系数，标准相关系数越大则说明与原信号相关性越强［26］。对于正常和故障状态下信号所得IMF 分量，计算IMF分量的峭度—标准相关系数指标，据此筛选有效IMF分量，不同状态信号所得IMF分量的两个评价指标如图5所示。由图5可知，在标准相关系数指标较小的情况下，两种状态下信号IMF7～IMF10 的峭度指标较小，因此选取IMF1～IMF6 作为有效IMF 分量，并计算其多尺度熵特征值。嵌入维数选取m= 2，相似容限取r= 0.2δ，尺度因子取τ= 15。部分信号IMF1～IMF6在不同状态下的多尺度熵值如图6所示。由图6可知，随着尺度因子增大，不同状态下IMF 分量的多尺度熵越发难以用于区分各个状态，选取IMF1～IMF6 尺度因子为2～5 的多尺度熵组建高维特征向量，输入ELM 进行模式识别。所构建的特征向量可由下式表示：

采用ELM 对尺度因子为2～5 的EEMD 多尺度熵特征集进行分类，ELM 的隐层神经网络个数设置为20，每种状态随机选取30 组作为训练集，剩下的样本作为测试集，不同状态EEMD多尺度熵特征向量集经ELM 训练后，进行一次实验的识别结果如图7所示。图7中，1 表示正常状态分类，2 表示故障状态分类。由图7可知，尺度因子为2～5 的EEMD 多尺度熵特征向量集，经ELM 后，能完全识别。采用EEMD 样本熵特征提取作为对比试验，将信号EEMD 样本熵作为特征向量，输入ELM 进行模式识别，所设定的参数同于EEMD 多尺度熵特征提取方法。每种状态下随机选取30 组作为训练集，余下各20 组作为训练集，EEMD 样本熵特征提取方法经ELM 后的识别结果如图8所示。由图8可知，EEMD 样本熵特征向量经一次ELM 识别后识别率低于EEMD 多尺度熵的识别率。实验次数过少容易导致识别结果存在较大差异，故两种方法各重复ELM 识别过程50次，每次实验随机选取60组样本为训练集，剩下样本为测试集，经重复ELM 模式识别后，两种方法的识别精度统计结果如表1所示。由表1可知，本文所提方法的识别精度更高，对于水电机组振动信号特征提取效果更优。

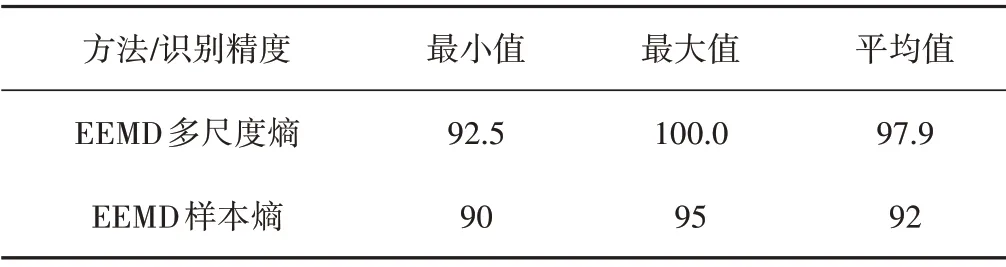
表1 经ELM重复识别50次不同方法识别精度统计 %Tab.1 The identification accuracy of different methods after repeating identification of ELM for 50 times

3.2 案例2

SK 电站3 号机组在2015年8月下旬，机组轴向振动剧烈，后经相关人员分析，发现机组转轮室里衬脱落，由水力不平衡因素引起机组轴向振动异常。采集得到机组发生故障前较长一段时间的轴向振动波形作为正常状态数据，机组刚发生故障时较短一段时间的轴向振动波形作为故障中数据，机组发生故障后的轴向振动波形作为故障后数据。采样频率为458 Hz，采样长度为4 096，不同状态各采集得到40组数据。

对原始振动信号进行非局部均值去噪处理，对降噪后信号进行EEMD 分解，随后采用峭度—标准相关系数指标筛选有效IMF分量。正常状态信号IMF分量峭度标准相关系数指标如图9所示，由图9可知，在标准相关系数指标较小的情况下，IMF8～IMF12 的峭度指标也较小，因此正常状态信号有效IMF分量为IMF1～IMF7。采用同样方法分析故障中和故障后信号的有效IMF 分量，经分析，该两种状态下的有效IMF 分量均为IMF1～IMF7，因此对于水口电站机组3种状态下轴向振动信号，选取IMF1～IMF7 作为有效IMF 分量并计算其多尺度熵值。嵌入维数选取m= 2，相似容限取r= 0.2δ，尺度因子取τ= 15。分析信号IMF1～IMF7在三种状态下的多尺度熵值，多尺度熵值区分较为明显的IMF 分量为IMF1～IMF4，部分信号IMF1～IMF4 的多尺度熵值计算结果如图10所示。由图10可知，选取尺度为2～5的IMF多尺度熵构建高维特征向量，区分效果明显。

将3种状态下IMF1～IMF7尺度因子为2～5的多尺度熵特征集输入ELM 进行模式识别，每种状态随机选取20 组作为训练，剩余共60 组特征集作为测试集。采用EEMD 样本熵特征提取方法做对比实验，计算信号IMF1～IMF7 的样本熵值作为特征集，每种状态随机选取20 组作为训练集，其余特征集作为测试集。为避免单次试验结果存在的偶然性，进行50 次ELM 重复训练与识别，每次识别随机选取60 组作为训练集，60 组作为测试集，两种方法识别精度统计结果如表2所示。由表2可知，本文所提方法具有更高的识别精度，在水电机组振动信号特征提取应用上具有更好的效果。

表2 经ELM重复识别50次不同方法识别精度统计 %Tab.2 The identification accuracy of different methods after repeating identification of ELM for 50 times

4 结 论

本文提出基于EEMD 多尺度熵和ELM 的水电机组振动信号特征提取方法，对信号进行EEMD 分解后采用峭度—标准相关系数指标筛选有效IMF 分量，并计算有效IMF 分量的多尺度熵，选取最佳尺度下的熵值构建故障特征向量集，将特征向量集输入ELM 进行模式识别。分别分析了水电机组实测顶盖振动信号和实测轴向振动信号，并采用EEMD 样本熵特征提取方法作对比试验，采用重复实验的方法避免了一次识别存在的偶然性。结果表明，本文所提的方法对于水电机组振动信号具有优良的特征提取效果，在实际工程中具有十分可观的应用前景。 □