黄麻纤维毡吸声特性及其在汽车上的应用
周文璐, 林萍, 徐晓美, 谢宇
(南京林业大学汽车与交通工程学院,南京 210037)
植物纤维来源广泛、绿色环保,其天然形成的相互贯通的多孔结构使得声波更容易产生能量耗散,从而使植物纤维材料具有较好的吸声性能[1-2]。近年来,植物纤维材料声学性能的研究吸引了越来越多研究人员的关注。Berardi等[3]对红麻、大麻、甘蔗等植物纤维材料吸声特性的研究表明,这些纤维材料在中、高频段具有较高的吸声系数。Putra等[4]对菠萝叶纤维样品中几种不同密度和厚度的材料进行了试验研究,结果表明当频率大于1 kHz时,这种植物纤维材料的平均吸声系数可达0.9。Prabhakaran等[5]研究了亚麻纤维增强复合材料的吸声和减振性能,结果表明亚麻纤维增强复合材料具有较高的吸声和减振性能。刘雪亭等[6]对木棉/中空聚酯纤维非织造材料声学性能的研究表明,在一定厚度和一定频率范围内该材料具有极好的吸声性能。彭立民等[7]对木质纤维/聚酯纤维复合材料吸声性能的研究表明,增加材料厚度或背腔深度,材料的吸声系数峰值将往低频方向移动。
目前关于植物纤维材料声学性能的研究,多数是基于试验测试开展的,研究结论尚不能从理论上有效指导植物纤维及其复合材料的声学性能设计。麻纤维是植物纤维中拉伸强度最好的品种之一。与其他麻类纤维相比,黄麻纤维密度最小,力学性能优异,是世界上产量最高、最廉价的天然纤维,具有加工性能良好的多孔结构。笔者以黄麻纤维毡为研究对象,基于阻抗管试验测得的吸声系数和运用粒子群优化算法辨识的非声学参数构建黄麻纤维毡的吸声模型,并基于此吸声模型开展其吸声特性影响因素及在汽车上的应用研究,以从理论上探讨黄麻纤维材料的吸声特性及其在汽车上应用的可行性。
1 黄麻纤维毡吸声模型
吸声性能通常以吸声系数为评价指标,材料的吸声系数可以通过描述特征阻抗和复数传播常数的材料基本特征参数推演得到,即通过构建材料的吸声模型预测得到。
目前,多孔材料吸声预测模型应用较多的有两种,即以Delany-Bazley(简称DB)模型为代表的经验模型和以Johnson-Champoux-Allard(简称JCA)模型为代表的唯象模型。经验模型仅需测量流阻率一个非声学参数,用归纳统计的方法,通过拟合大量阻抗管试验数据,分别建立特征阻抗与流阻率、传播常数与流阻率和声波频率之间的幂指函数关系,因此模型简单,能快速预测结果。但是经验模型没有考虑孔隙的微观结构,且每种经验模型仅适用于预测一种类型的材料和某些频率范围的吸声系数,因此不具有普遍适用性[8]。唯象模型不同于经验模型,它考虑了黏滞和热传导效应等微观因素对声能的影响,引入流阻率、孔隙率、曲折因子、黏性特征长度以及热特征长度等5个特征参数描述材料性质,构建了多孔材料微观结构和吸声系数之间的关系,因此计算精度较高且参数物理意义清晰,目前得到了较多的应用[9]。
吸声模型的选择应基于吸声机理和孔隙率类型,结合黄麻纤维毡的吸声机理及其结构特点,选用JCA模型表征其吸声性能。该模型对材料的动态密度ρeff和有效体积模量Keff的描述如式(1)和式(2)所示:
(1)
(2)
式中:j为虚数单位;α∞为曲折因子;ρ0为空气密度;σ为材料的流阻率;φ为材料的孔隙率;ω为入射声波的角频率;η为空气的动力黏度,η=1.84×10-5N·s/m2;γ为空气的比热容比,γ=1.4;P0为大气压强;Npr为普朗克常数,用Npr= 0.702来表示空气常数;Λ为黏性特征长度,Λ′为热特征长度,其计算式可分别表示为:
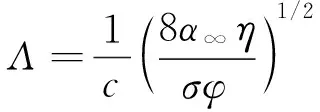
其中c和c′分别为孔的横截面形状因子和截面因子。
由式(1)和式(2)可表征材料的特征阻抗Zc和复数传播常数Kc:
(3)
(4)
考虑厚度为d的多孔材料背衬刚性壁面的情况,吸声系数α可由式(5)~(7)表达:
(5)
(6)
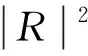
(7)
式中:R为材料的声压反射系数;d为样品的厚度;Zs为材料的表面阻抗;Z0为空气特征阻抗。
2 吸声模型参数辨识
在一般试验条件下,除了材料的孔隙率外,JCA吸声模型中的其余4个非声学参数的直接测量都较为困难。黏性特征长度、热特征长度以及材料曲折因子的测量需要用到超声方法,并且试验设备昂贵[10]。因此,考虑采用逆向求解方法获取其余参数,即从相对容易测得的材料参量反求理论模型中难以直接测得的非声学参数。JCA吸声模型中有4个非声学参数需要辨识,即流阻率、曲折因子、黏性特征长度和热特征长度,其辨识思想是根据计算得到的孔隙率和阻抗管测得的吸声系数,依据一定的算法,通过拟合模型逆推JCA吸声模型中的未知参数。
2.1 算法设计
PSO算法,即粒子群优化算法(particle swarm optimization algorithm),是求解声学参数逆问题的一种高效可行的算法。PSO算法对初始化的一群随机粒子(随机解),通过多次迭代寻找最优解。在每一次的迭代中,粒子通过跟踪两个“极值”(Pbest,Gbest)来更新自己。在找到这两个最优值后,粒子通过式(8)和式(9)来更新自己的速度和位置:
(8)
(9)
算法目标是寻求最优变量使模型预测值与试验值吻合程度最佳,故将各个频率下吸声系数的试验值与模型预测值误差的平方和最小值作为目标函数,即目标函数fobj为:
(10)
式中:αexp(fi)为在不同频率点实验室测得的材料吸声系数;αJCA(P,fi)为在各频率点用JCA模型预估得到的材料吸声系数;P为样本的4个非声学参量,定义为P=[σ,α∞,c,c′]。
由文献[11]可知,常用声学多孔材料的测量表明,材料的曲折因子通常不小于1且不大于4。由于材料的热特征长度通常不小于黏性特征长度,由式(3)可知,材料的形状因子c不小于材料的截面因子c′,且c、c′的常用取值范围为[0.3,3.3]。由文献[12]可知,材料的流阻率通常在[1 000, 200 000]。为此,4个特征参量约束条件可写作:
(11)
在MATLAB软件中编写相应的粒子群优化算法程序,设置相关的算法参数,其参数设置情况陈述如下:文献[13]的研究表明,惯性权重w在[0.8,1.2]时PSO具有更快的收敛速度,本研究兼顾局部寻优能力,将w设为0.8;合适的c1、c2可以加快收敛且不易陷入局部最优[13],通常令c1=c2=2;空间维数D由优化问题决定,即自变量的个数,本研究待辨识的材料参数有4个,因此维数D取作4;一般粒子种群个数的多少取决于待优化问题的复杂程度,初始种群越大收敛性会越好,但过大的种群会影响优化速度,因此本研究设定初始种群为100个;优化计算时,一般迭代次数太少,会使求解结果不稳定,迭代次数越多,求解精度越高,但计算量也越大,兼顾精度和计算量,本研究设定迭代次数为300。
2.2 辨识结果
通过热黏合工艺得到的黄麻纤维毡,采用图1所示的声学阻抗管测试系统测量其吸声系数。测试所采用的黄麻纤维毡的孔隙率为0.976 2,用于阻抗管大直径管的样件厚度为18.93 mm,小直径管的样件厚度为18.65 mm,因此,黄麻纤维毡的平均厚度为18.79 mm。阻抗管的大直径管适用于250~1 600 Hz频率范围内吸声系数的测量,小直径管适用于500~6 300 Hz频率范围内吸声系数的测量。对在500~1 600 Hz重叠频率范围内测得的吸声系数可按式(12)进行计算[14]:
(12)

图1 声学阻抗管测试系统Fig. 1 Impedance tube testing system
式中,αS和αL分别代表样品在小直径管和大直径管中测得的吸声系数。
基于试验所得到的黄麻纤维毡的吸声系数及设计的粒子群优化算法,可辨识出JCA吸声模型中的4个非声学参数值,如表1所示。将采用PSO算法辨识到的非声学参数值代入到JCA吸声模型中,计算出基于理论模型预测的黄麻纤维毡的吸声系数。图2即为在频率250~6 300 Hz范围内,黄麻纤维毡的试验测量吸声系数曲线与JCA模型预测吸声系数曲线。

表1 JCA模型中4个非声学参数的辨识值Table 1 Identification values of four non-acoustic parameters in JCA model
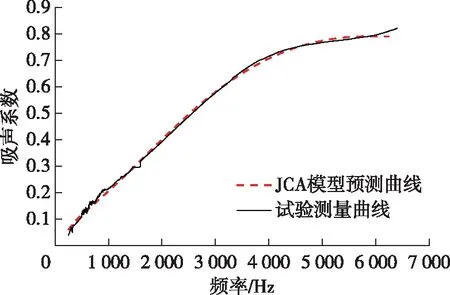
图2 吸声系数试验测量曲线与JCA模型预测曲线Fig. 2 Experimental curve and predicted curve by JCA model for the sound absorption coefficient
由图2可以看出,黄麻纤维毡的吸声系数随着频率的增加而提高,在高频范围内具有较好的吸声性能,其最大吸声系数可达0.82。在整个分析频率范围内,由JCA吸声模型预测得到的黄麻纤维毡的吸声系数曲线与试验得到的曲线具有较好的一致性,两根曲线几乎重叠。这表明所提出的PSO参数辨识算法是可靠的,基于辨识参数建立的JCA吸声模型能较好地描述黄麻纤维毡的吸声性能。
3 吸声特性影响因素分析
基于以上参数辨识得到的黄麻纤维毡JCA吸声模型,研究黄麻纤维毡的厚度、流阻率、孔隙率、曲折因子、黏性特征长度与热特征长度对其吸声特性的影响。
3.1 黄麻纤维毡厚度对吸声系数的影响
王东[15]对不同厚度木纤维/聚酯纤维复合材料的吸声特性开展了研究,结果表明,当厚度增加为原来的两倍时,共振吸收峰值相应地向低频移动一半,即随着材料厚度的增加,材料的低频吸声能力得到了提高。Taban等[16]对天然椰纤维的吸声性能进行了研究,研究发现在较低的频率范围内,增加样品的厚度可以提高椰纤维的曲折因子、黏性特征长度和热特征长度,从而提高材料在低频段的吸声系数。可见,厚度对植物纤维在低频段的吸声性能有影响。
为研究黄麻纤维毡的厚度对其吸声特性的影响,在其他材料参数不变的情况下,取厚度值分别为13.79,18.79,23.79和33.79 mm,基于JCA吸声模型仿真得到4组厚度所对应的吸声系数曲线,如图3所示。由图3可以看出,黄麻纤维毡的厚度对其吸声系数具有显著的影响。吸声系数随着材料厚度的增大而整体增大,吸声系数峰值所对应的频率随着材料厚度的增大向低频区域移动,即增加黄麻纤维毡的厚度能显著提高其中、低频的吸声能力。

图3 黄麻纤维毡厚度对吸声系数的影响Fig. 3 Influence of thickness of the jute fiber felt on the sound absorption coefficient
3.2 黄麻纤维毡孔隙率对吸声系数的影响
孔隙率表示多孔材料中饱和流体(一般为空气)的体积与材料总体积之比,一般多孔材料的孔隙率大于70%,多数可达到90%以上。
为研究黄麻纤维毡的孔隙率对其吸声特性的影响,在其他材料参数不变的情况下,取孔隙率值分别为0.776 2,0.876 2和0.976 2,基于JCA吸声模型仿真得到3组孔隙率所对应的吸声系数曲线,如图4所示。
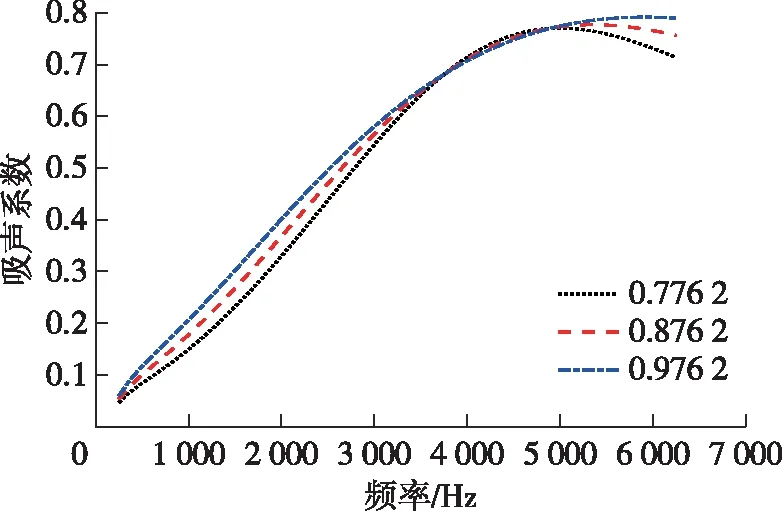
图4 黄麻纤维毡孔隙率对吸声系数的影响Fig. 4 Influence of porosity of the jute fiber felt on the sound absorption coefficient
由图4可知,在整个频率范围内,随着黄麻纤维毡孔隙率的增大,同一频率范围内的吸声系数增大。这是由于增大材料孔隙率,就增加了材料内部的孔隙数量,从而增加了声波在孔隙间的反射和折射次数,加剧了声波与孔隙的摩擦和空气黏滞消耗,继而增加了声波的损耗[17]。但总体而言,黄麻纤维毡孔隙率增加对其吸声系数的影响并不是特别显著,尤其在3 500~5 000 Hz范围内,孔隙率对黄麻纤维的吸声系数几乎没有影响。
3.3 黄麻纤维毡流阻率对吸声系数的影响
流阻率是对材料吸声性能影响最为重要的物理参数之一,定义为空气流经单位厚度多孔材料时所受到的阻力,单位为N·s/m4。姚丹等[18]通过对动车床垫材料流阻与吸声系数关系的研究发现,增大流阻率使材料的平均吸声系数呈先增大后减小的趋势。为研究黄麻纤维毡的流阻率对其吸声特性的影响,在其他材料参数不变的情况下,取流阻率值分别为7 421,12 421,17 421 和22 421 N·s/m4,基于JCA吸声模型仿真得到4组流阻率所对应的吸声系数曲线,如图5所示。
由图5可知,黄麻纤维毡的吸声系数随频率的增大而增大,随流阻率的增大而增大,并且在分析频率范围内,频率越高,流阻率对材料吸声系数的影响越显著。
3.4 黄麻纤维毡曲折因子对吸声系数的影响
多孔材料的曲折因子是一个结构无量纲参数,是体现孔隙结构复杂度的因子,也称之为结构形状因子,其反映空腔内部结构对宏观气流速度的影响,它只取决于多孔材料的几何形状。
为研究黄麻纤维毡的曲折因子对其吸声特性的影响,在其他材料参数不变的情况下,取曲折因子值分别为1,1.5,2.5和3.5,基于JCA吸声模型仿真得到4组曲折因子所对应的吸声系数曲线,如图6所示。
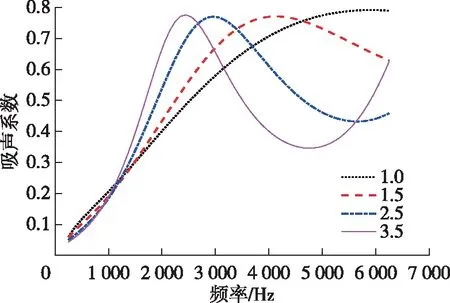
图6 黄麻纤维毡曲折因子对吸声系数的影响Fig. 6 Influence of tortuosity of the jute fiber felt on the sound absorption coefficient
由图6可以看出,在分析频率范围内,曲折因子对黄麻纤维毡的吸声系数峰值大小的影响并不明显,但对吸声系数峰值所对应的频率影响较显著,随着曲折因子的增大,吸声系数峰值所对应的频率向低频区域移动,高吸声系数的频段变窄。当曲折因子为2.5和3.5时,在分析频率范围内,吸声系数曲线呈现出明显的峰值和谷值。
3.5 黄麻纤维毡黏性特征长度对吸声系数的影响
黏性特征长度用于描述高频下孔隙中的流体与固体框架间的黏滞力大小,它只取决于多孔材料单元的几何结构或尺寸。
为研究黄麻纤维毡的黏性特征长度对其吸声特性的影响,在其他材料参数不变的情况下,取黏性特征长度值分别为157,207 和257 μm,基于JCA吸声模型仿真得到3组黏性特征长度所对应的吸声系数曲线,如图7所示。

图7 黄麻纤维毡黏性特征长度对吸声系数的影响Fig. 7 Influence of viscous characteristic length of the jute fiber felt on the sound absorption coefficient
由图7可以看出,在整个分析频率范围内,黏性特征长度对黄麻纤维毡的吸声系数影响都不显著,尤其在2 500 Hz以下,几乎没有影响,在2 500 Hz以上,略有影响,较小的黏性特征长度能使黄麻纤维毡获得稍大的吸声系数。此外,从图中还可以看出,黏性特征长度为207 和257 μm的吸声系数曲线近似重合,这意味着当黏性特征长度较大时,再增加黏性特征长度对黄麻纤维毡的吸声性能并没有影响。
3.6 黄麻纤维毡热特征长度对吸声系数的影响
热特征长度用于描述高频下孔隙中的流体与固体框架间的热交换程度,它同样取决于多孔材料单元的几何结构,与单元内流体流动的类型无关。
为研究黄麻纤维毡的热特征长度对其吸声特性的影响,在其他材料参数不变的情况下,取热特征长度值分别为223,273 和323 μm,基于JCA吸声模型仿真得到3组热特征长度所对应的吸声系数曲线,如图8所示。

图8 黄麻纤维毡热特征长度对吸声系数的影响Fig. 8 Influence of thermal characteristic length of the jute fiber felt on the sound absorption coefficient
由图8可见,在整个分析频率范围内,热特征长度对黄麻纤维毡的吸声系数影响也比较小。黄麻纤维毡的吸声系数随频率增加而增加,随热特征长度的减小而略有增加。与黏性特征长度的影响类似,当热特征长度较大时,再增加热特征长度对黄麻纤维毡的吸声性能影响很小。
4 黄麻纤维材料在汽车上的应用
在汽车声学包装中,常用纤维材料作为吸声材料。植物纤维因其制备工艺简单、绿色环保、价格低廉等优势,被越来越多地用到汽车上作为汽车坐垫、衬垫等汽车内饰吸声材料[19]。
田秀洁等[20]研究了由两层不同密度组合成的毛毡类多孔材料有PE膜和无PE膜时的车内隔音垫的吸声性能。取与文献[20]中隔音毛毡相同厚度的黄麻纤维毡,基于JCA吸声模型得到其吸声系数曲线,并与文献中给出的用在汽车上的毛毡材料的吸声系数曲线作比较,如图9所示。

图9 车用毛毡与黄麻纤维毡的吸声系数曲线Fig. 9 Sound absorption coefficient curves for the felt used in automobiles and the jute fiber felt
由图9可见,除了在4 000~5 500 Hz频率范围内,黄麻纤维毡的吸声系数略低于车用传统毛毡类多孔材料,在分析频率范围的其他频段,黄麻纤维毡的吸声系数均高于车用传统毛毡类多孔材料,尤其在2 000 Hz左右,黄麻纤维毡的吸声系数接近于1。这意味着黄麻纤维毡具有比车用传统毛毡类材料更好的吸声特性,可望替代车用传统毛毡,成为绿色环保的车用吸声材料。
5 结 论
笔者开展了黄麻纤维毡的吸声模型、吸声特性影响因素及其在汽车上的应用研究,所得结论如下:
1)黄麻纤维毡在高频范围内具有较好的吸声性能,其最大吸声系数可达0.82。
2)提出的粒子群优化算法用于辨识JCA模型中非声学参数是可靠的,基于辨识参数建立的JCA吸声模型能较好地描述黄麻纤维毡的吸声性能。
3)黄麻纤维毡的厚度、流阻率和曲折因子都对其吸声系数具有显著影响,孔隙率、黏性特征长度和热特征长度对其吸声系数的影响较小。黄麻纤维毡的吸声系数随其厚度和流阻率的增大而增大,厚度增大可显著提高其中、低频吸声能力,在高频区流阻率对吸声系数的影响更加显著;曲折因子的增大会使黄麻纤维毡的吸声系数峰值所对应的频率向低频区域移动,并且高吸声系数的频段变窄。
4)黄麻纤维毡具有比车用传统毛毡类材料更好的吸声特性,可望替代车用传统毛毡,成为绿色环保的车用吸声材料。

